Тіла обертання. Куля, сфера. Перебийніс Світлана Миколаївна вчитель математики Смілянської загальноосвітньої школи І-ІІІ ступенів № 10 Геометрія, 9 клас
Оберіть розділ: • • Основні поняття Типові задачі Задачі на знаходження об’єму кулі Задачі на знаходження поверхні сфери Комбіновані задачі Кульові форми навколо нас Історична довідка Список використаних джерел
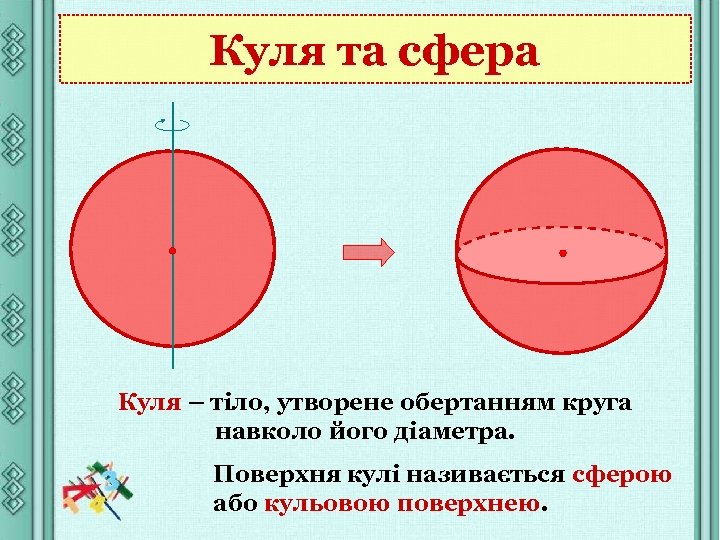
Куля та сфера Куля – тіло, утворене обертанням круга навколо його діаметра. Поверхня кулі називається сферою або кульовою поверхнею.
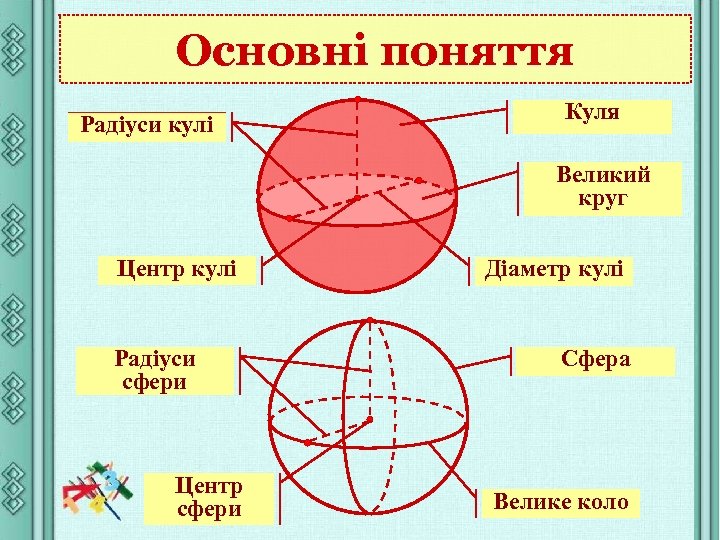
Основні поняття Радіуси кулі Куля Великий круг Центр кулі Радіуси сфери Центр сфери Діаметр кулі Сфера Велике коло
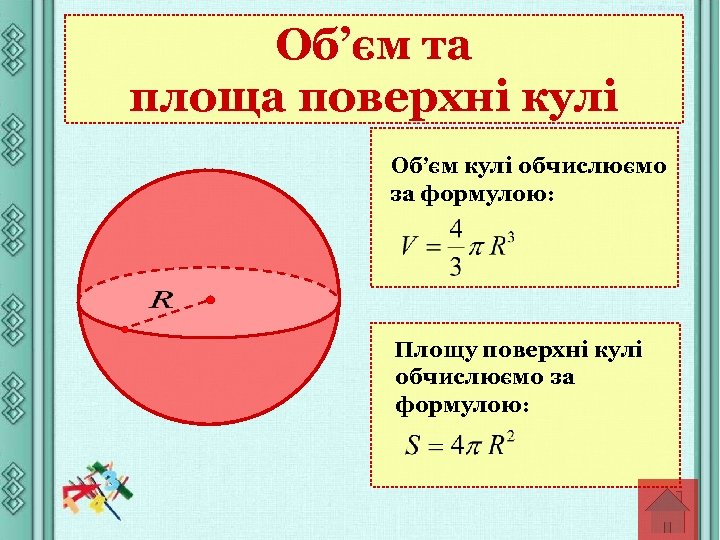
Об’єм та площа поверхні кулі Об’єм кулі обчислюємо за формулою: Площу поверхні кулі обчислюємо за формулою:
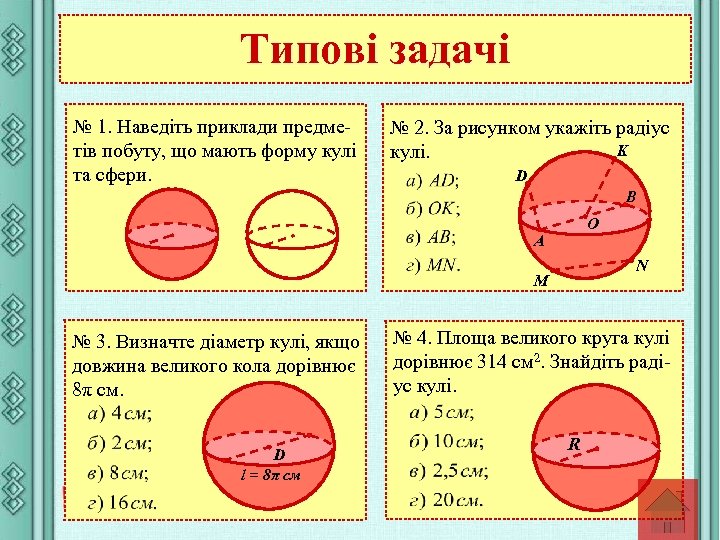
Типові задачі № 1. Наведіть приклади предметів побуту, що мають форму кулі та сфери. № 2. За рисунком укажіть радіус K кулі. D B O A N M № 3. Визначте діаметр кулі, якщо довжина великого кола дорівнює 8π см. D l = 8π см № 4. Площа великого круга кулі дорівнює 314 см 2. Знайдіть радіус кулі. R
Задачі на знаходження об’єму кулі № 1. Об’єм кулі, радіус якої дорівнює 6, обчислюємо так: № 2. Знайдіть об’єм кулі, довжина великого кола якої 6π см. l = 6π см № 3. Визначте об’єм кулі, діаметр якої дорівнює 6 см. D № 4. Знайдіть радіус кулі, об’єм якої дорівнює 36π см 3: R
Задачі на знаходження поверхні сфери № 1. Радіус сфери дорівнює 7 см. Знайдіть площу поверхні сфери. № 2. Площа поверхні кулі дорівнює 100π см 2. Знайдіть діаметр кулі. R № 3. Обчисліть площу повної поверхні півкулі, якщо її діаметр дорівнює 20 см. № 4. Площа великого круга кулі дорівнює 314 см 2. Знайдіть площу поверхні кулі. R
Комбіновані задачі на об’єми куль № 1*. Свинцеву кулю розплавили і переплавили в кульки, радіус яких у 3 рази менший. Скільки таких кульок дістали? Розв’язання. Нехай дістали п кульок, радіус яких R, тоді радіус великої кулі 3 R. Маємо рівняння: № 2*. Три кулі, радіуси яких 3 см, 4 см і 5 см сплавили в одну кулю. Знайдіть її радіус. Розв’язання. Нехай V і R – об’єм і радіус нової кулі, а V 1, V 2, V 3 – радіуси даних куль. Маємо рівняння: Відповідь. 27 кульок. Відповідь. 6 см.
Комбіновані задачі на об’єми та поверхні тіл № 3*. Чи є така куля, у якої об’єм і поверхні виражаються одним і тим самим числом? Розв’язання. Нехай V і Sсф. – об’єм і площа поверхні кулі, радіусом R. Маємо рівняння: № 4*. Об’єм однієї кулі у 8 разів більший від об’єму другої. У скільки разів площа сфери першої кулі більша від площі сфери другої кулі? Розв’язання. Нехай V 1, R 1, S 1 та V 2, R 2, S 2 – об’єм, радіус та площа поверхні відповідно першої та другої куль. Отже, у кулі радіусом 3, об’єм і поверхня однакові. Відповідь. Така куля є. Радіус кулі 3. Відповідь. У 4 рази.
Задачі на комбінації тіл № 5*. Куля і конус мають однакові об’єми. Радіус кулі дорівнює радіусу конуса. У скільки разів висота конуса більша від радіуса кулі? Розв’язання. Нехай V 1, R 1 та V 2, R 2, H – об’єми, радіуси та висота відповідно кулі та конуса. Маємо: № 6*. У скільки разів об’єм півкулі, радіус якої дорівнює R, більший за об’єм конуса, у якого висота та радіус дорівнюють R? Відповідь. В 4 рази. Відповідь. В 2 рази. Розв’язання. Нехай V 1, R 1 – об’єм та радіус півкулі, V 2, R 2, H 2 – об’єм, радіус та висота конуса. За умовою маємо: R 1 = R 2 = H = R. Маємо:
Кульові форми навколо нас Водно-гелієві кулі Сонячної системи: Сонце, Юпітер, Сатурн, Уран, Нептун
Історична довідка • Куля (від грецького σφαίρας). Куля • Сфера походить від грецького фера слова «сфайра» , яке перекладається як «м’яч» . • Архімед (бл. 287 -212 до н. е. ) – Архімед давньогрецький учений, конструктор, винахідник. Один з перших показав, як обчислювати площу поверхні кулі та її об’єм. Це він зазначив у праці «Про кулю і циліндр» .
Список використаних джерел: 1. Апостолова Г. В. Геометрія. 9 клас: Дворівневий підручник для загальноосвітніх навчальних закладів. – К. : Генеза, 2009. – 304 с. 2. Тарасенкова Н. А. Елементи стереометрії в основній школі. Уроки стереометрії в 9 класі: Методичний посібник для вчителів загальноосвітніх навчальних закладів. – Х. : Веста: Ранок, 2002. – 128 с. 3. Істер О. С. Усні вправи з алгебри та геометрії. 11 клас. : – Т. : Підручники і посібники, 2002. – 64 с. 4. Возняк Г. М. , Підручна М. В. , Моховик О. В. , Кулешко В. І. Математика. Контроль навчальних досягнень. Збірник завдань. 11 клас. Рівень стандарту: Навчальний посібник. – Т. : Підручники і посібники, 2012. – 80 с. 5. Возняк Г. М. , Бабій Н. В. Математика. 11 клас. Збірник тестових завдань. Рівень стандарту: Навчальний посібник. – Т. : Підручники і посібник, 2011. – 128 с. 6. Сайт “Вивчаємо математику”. http: //www. testmath. com. ua/. 7. Сайт “Математика для школи”. http: //formula. co. ua/.
Скачать презентацию Тіла обертання Куля сфера Перебийніс Світлана Миколаївна вчитель
261d821eee475e89d78a3aa64872fcbf.ppt