Three Ways to Take Algebra II and Still

Three Ways to Take Algebra II and Still Enroll in Career-Tech Wayne-Westland Community Schools William D. Ford Career-Technical Center Westland, MI Kathleen Williams – Secondary Math Instructor Michael Koelzer – Construction Technology Instructor

Three Methods Extended Algebra II Moodle Algebra II Embedded Algebra II

Extended Algebra II Students Enroll in both CTE class and Algebra II Students receive 1 credit per semester from CTE class Students receive ½ credit from Algebra II Students attend Algebra II every day for 50 minutes at WDFCTC and Math Instructors and follow Wayne. Westland district pacing guide for Extended Algebra II Advantage – Students can attend CTE center. Disadvantage – CTE Instructors must modify instruction time and/or requirements for missed “skill” time in CTE class.

Moodle Algebra II Traverse Bay Area Intermediate School District www. tbaisd. k 12. mi. us Health Occupation, Medical Assisting and Child Care Students Enroll in both CTE class and Moodle Algebra II. Students receive 1 credit per semester from CTE class Students receive ½ credit from Algebra II Students attend Algebra II every day for 50 minutes at WDFCTC and Math Instructors and follow a modified curriculum for 2 nd year Extended Algebra II (Family of Functions is taught 1 st semester as a general overview and Trig is not taught 2 nd semester. ) Advantage – Students can attend CTE center and be out of Algebra II by early April so that they can attend their clinicals full-time. Disadvantage – Math Instructor has to teach complete lessons to Moodle students (who are attending mini-clinicals which last up to two weeks) after school up to 4 days a week until the math has been covered.

Embedded Algebra II Students stay in their CTE class full-time. Math Instructor teaches once a week in the CTE classroom CTE Instructor repeats instruction as needed over the week Advantage – Students have some project based lessons Disadvantage – Depth of all Algebra II is not attainable with this format.

A 1. 2. 9 Know common formulas (e. g. , slope, distance between two points, quadratic formula, compound interest, distance = rate*time), and apply appropriately in contextual situations. CONSTRUCTION : Find the length of rafter c (NOTE: Do not include any overhang) c 7’ 17’ ELECTRONICS: E = I*R P = E*I I = P/E E = P/I R = E/I P = I 2*R R = P/I 2 I= P/R I = E/R P = E 2/R R = E 2/P E= P*R RT = R 1+R 2+R 3 RT = (R 1*R 2)/(R 1+R 2) WELDING: Hypotenuse = leg A c=5 c 45 o-90 o Triangle 2 2 c b 90 o B 45 o C a a=b c=b 2 or a 2

L 1. 2. 1 Use mathematical symbols (e. g. , interval notation 0 ≤ x ≤ 5; set notation {1, 2, 3}; summation notation) to represent quantitative relationships and situations. CONSTRUCTION: Solder copper pipes into a square (6”) 1/8” tolerance. 5 7/8 ≤ x ≤ 6 1/8 ELECTRONICS: Resistor color code: Red, Black, Orange, Gold 20, 000 ± 5% 21, 000 19, 000 Yellow, Green, Brown, Silver 450 ± 10% 495 405 WELDING: 1” top view of box 4” 5” Center the hole on the plate 1 1/8” ± 1 1/16” to 1 3/16” 1 1/16” ≤ x ≤ 1 3/16”

L 3. 2. 1 Determine what degree of accuracy is reasonable for measurement in a given situation; express accuracy through use of significant digits, error tolerance, or percent of error; describe how errors in measurement are magnified by computation; recognize accumulated error in applied situations. CONSTRUCTION, ELECTRONICS, WELDING: Tolerance example: Gap (in mm) |x+0. 5| < 0. 5 -0. 5 < x+0. 5 < 0. 5 = -1. 0 < x < 0

L 1. 3. 1 Describe, explain, and apply various counting techniques (e. g. , finding the number of different 4 -letter passwords; permutations; and combinations); relate combinations to Pascal’s triangle; know when to use each technique. CONSTRUCTION: How many different combinations of 2 bits, 1 hammer, and 1 drill can be chosen? The shop has: 40 Drill Bits 12 Hammers 10 Drills 40 C 2 * 12 C 1 * 10 C 1 = 112, 320 Combinations ELECTRONICS: How many different combinations of 2 resistors, 1 capacitor, and 1 inductor? The shop has: 40 Resistors 12 Capacitors 40 C 2 * 12 C 1 * 10 C 1 = 112, 320 Combinations 10 Inductors WELDING: How many different combinations of exactly 2 pieces of metal, 1 brush, 1 hammer, and 1 hood can be chosen? 40 Pieces of Metal 18 Brushes 12 Chipping Hammers 10 Welding Hoods 40 C 2 * 18 C 1 * 12 C 1 * 10 C 1 using a calculator: 780 * 18 * 12 * 10 = 1, 684, 800 Possible Combinations

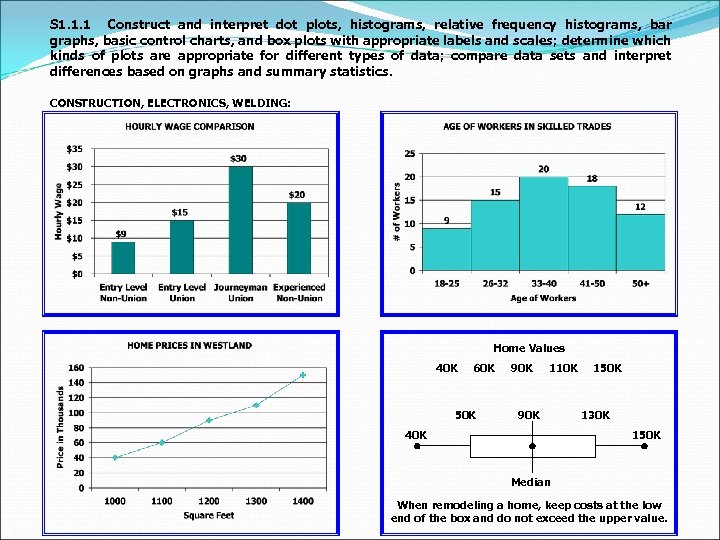
S 1. 1. 1 Construct and interpret dot plots, histograms, relative frequency histograms, bar graphs, basic control charts, and box plots with appropriate labels and scales; determine which kinds of plots are appropriate for different types of data; compare data sets and interpret differences based on graphs and summary statistics. CONSTRUCTION, ELECTRONICS, WELDING: Home Values 40 K 60 K 50 K 90 K 110 K 90 K 40 K 150 K 130 K 150 K Median When remodeling a home, keep costs at the low end of the box and do not exceed the upper value.

S 1. 2. 1 Calculate and interpret measures of center including: mean, median, and mode; explain uses, advantages and disadvantages of each measure given a particular set of data and its context. . CONSTRUCTION, ELECTRONICS, WELDING: Looking at the home prices from S 1. 1. 1 write a scenario that would best fit selecting the mean. Repeat for median and mode. Example: Choose the mean if determining the average cost of a 1400 sq. ft. house with similar configurations such as 2 bedroom 1 ½ bath with 2 car garage. Choose the mode to determine what size (sq. ft. ) of homes that were selling the most in a subdivision or particular school zoned area. Choose the median to determine the average house price in a subdivision or section of a city.

A 1. 1. 4 Add, subtract, multiply, and simplify polynomials and rational expressions (e. g. , multiply (x-1) (1 -x 2+3); simplify (9 x-x 3)/(x+3)). CONSTRUCTION: [2 x 2 – 6 x + 4](x-1) 2 x 3 – 6 x 2 + 4 x – 2 x 2 + 6 x – 4 2 x 3 -8 x 2 + 10 x – 4 ELECTRONICS: RT = (R 1*R 2)/(R 1+R 2) Let R 1 = 2 x and R 2 = 6 x RT = (2 x*6 x)/2 x + 6 x) RT = 12 x 2 / 8 x RT = 3/2 x WELDING: [(5 -2 x) (4 -2 x)]x [20 -8 x-10 x+4 x 2]x [20 -18 x+4 x 2]x 20 x-18 x 2+4 x 3

A 1. 2. 5 Solve polynomial equations and equations involving rational expressions (e. g. , solve -2 x(x 2+4 x+3) = 0; solve x-((1/(x+6)) = 3, and justify steps in the solution. CONSTRUCTION: V = L*W*H 36 = (2 x-2) (x-1) 36 = [2 x 2 - 2 x - 4 x +4](x-1) Foil binomials 36 = [2 x 2 – 6 x + 4](x-1) Combine like terms 36 = 2 x 3 – 6 x 2 + 4 x – 2 x 2 + 6 x – 4 Distribution property 36 = 2 x 3 -8 x 2 + 10 x – 4 Combine like terms 0 = 2 x 3 - 8 x 2 + 10 x + 32 Subtraction property ELECTRONICS: RT = (R 1*R 2)/(R 1+R 2) Let RT = 72 ohms, R 1 = 2 x and R 2 = 6 x RT = (2 x*6 x)/2 x + 6 x) Substitution Property RT = 12 x 2 / 8 x Multiplication Property and combine like terms 72 = 3/2 x Division Property of Exponents and Reducing Fractions X = 16 ohms Division Property of Fractions WELDING: V = L*W*H 6 = [(5 -2 x) (4 -2 x)]x 6 = [20 -8 x-10 x+4 x 2]x 6 = [20 -18 x+4 x 2]x 6 = 20 x-18 x 2+4 x 3 0 = 4 x 3 -18 x 2+20 x-6 Foil Binomials Combine like terms Distribution property Subtraction property

A 3. 1. 2 Adapt the general symbolic form of a function to one that fits the specifications of a given situation by using the information to replace arbitrary constants with numbers. CONSTRUCTION: Find the number of studs in a 37’ wall x = L*. 75+1 x = 37*. 75+1 X = 29 ELECTRONICS: Resonant Frequency Formula f = 1/(2 л LC) Determine the frequency in KHz given an 330 µH Inductor and a. 22 µF Capacitor. f = 159. 2/ 330*. 22 f = 18. 68 KHz WELDING: c 2 = a 2+b 2 52 = 42+22 25 = 16+4 25 > 20 Angle is obtuse 5 4 ? 2

A 1. 1. 7* Transform trigonometric expressions into equivalent forms using basic identities. ELECTRONICS: Z Xc TAN = Xc/R SIN = Xc/Z COS = R/Z Tp = E*I*COS R A 2. 2. 4* If a function has an inverse, find the expression(s) for the inverse. ELECTRONICS: W=2 f T = 1/f f = 1/T Xc = 1/(2 f C) XL = 2 f L FR= 1/(2 л LC)

A 2. 9. 1 Write the symbolic form and sketch the graph of simple rational functions. CONSTRUCTION: Build a wooden box of 1” material. Outside dimensions are L = 2*H and L = 2*W. Total volume = 36 square inches. x V = L*W*H 36 = (2 x-2) (x-1) x 2 x ELECTRONICS: WELDING: Using a graphing calculator: Volume = 6 and x = 1 x x 4” x x x 5” x V = L*W*H 6 = [(5 -2 x) (4 -2 x)]x 6 = [20 -8 x-10 x+4 x 2]x 6 = [20 -18 x+4 x 2]x 6 = 20 x-18 x 2+4 x 3 0 = 4 x 3 -18 x 2+20 x-6

Embedded Algebra - Construction A 2. 9. 1 Using Rational Functions in Construction

Embedded Algebra - Construction A 2. 9. 1 Using Rational Functions in Construction Do not lose this sheet! You must build a box for a customer that will hold exactly 162 cubic inches of sand. The box will be made from ½ inch material, with 4 sides and a bottom, but no top. The length must be twice the width, and the height will be the same as the width. You will first use algebra to determine the size of the box. Next you will build the box. Finally you will test the size of the box with sand. Do your math on this page and turn this in with your box.

Embedded Algebra - Construction Evaluation: Safety: 5 Math: 15 Sand Test: 10 Measurements: 10 Square: 5 Cuts: 5 Total: 50 points (Test Grade)

Embedded Algebra - Construction

Embedded Algebra - Construction And they all lived happily ever after. . .

References Moodle Sites www. tbaisd. k 12. mi. us www. moodle 2. resa. net/ww WDFCTC Website http: //ford. wwcsd. net/ Presenter’s Emails williamskr@wwcsd. net koelzerm@wwcsd. net