a6e88c913bbfcc0c7de3fb5ff04d9aec.ppt
- Количество слайдов: 67

Three basic concepts: 1. Decision Problems: output yes/no 2. Nondeterministic algorithm: certificate additional input 3. Polynomial transformation: one problem input to another type problem input in poly-time (C) Debasis Mitra

1. DECISION PROBLEMS • Decision Problems: output is “True/False, ” “Yes/No” • Example (sorting-decision problem): – Input: a list of numbers L – Output, an answer: is L sorted? • Complexity of Decision Problem? – Sorting problem P: lower bound Ω(n logn), but – Sorting-decision problem PD : O(n) (C) Debasis Mitra

ADVANTAGE OF DECISION PROBLEMS • Every problem P has a corresponding related decision problem PD, – Has a lesser or equal complexity – Logical output to work with makes it formal • Hence, complexity theory (or, any computer science formal theory) uses only decision problems • But, the results are valid for all types of problems (C) Debasis Mitra

EXAMPLE DECISION PROBLEM • Example (0 -1 Knapsack-decision problem): – Input: a list of objects with (weight, profit), a knapsack upper bound by weight M, and a profit lower bound t – Output: Does there exist a ks_profit ≥ t by choosing some objects with ks_wt ≤ M? • Complexity? • Which one is lower – original 01 KS or 01 KSD? • 01 KSD algorithm: Backtrack just like before for 01 KS but may terminate as soon as a valid ks_profit ≥ t found, need not go over all branches. (C) Debasis Mitra

USE OF DECISION PROBLEMS • Algorithm A(PD ) for a decision problem PD may be used to solve original problem P, and vice versa • Example of sorting, using sorting-decision algorithm: – Sort (input L): • For each permutation p of input list L • if Algo. Sorting. D (p) == True then return p; – Sorting. D (input L): If any comparison within the algorithm Sorting(L) leads to an actual exchange of elements, then return “False” (L was not sorted) • Similarly Alg(01 KSD) may be used to solve 0 -1 KS: Hint: binary search over ks_profit bound variable t • Reverse is easy: ? ? (C) Debasis Mitra

MORE CONCEPTS: : : 2. NON-DETERMINISTIC ALGORITHMS (C) Debasis Mitra

NON-DETERMINISIM • Non-deterministic version of a problem: • Presume the solution exists: “certificate” • Problem is simplified: Check only the certificate, Is the certificate correct answer? – return “True/False” • If an algorithm can check certificate in polynomial time • => The problem is Non-deterministically Polynomial, • in NP-class (C) Debasis Mitra

NON-DETERMINISTIC PROBLEMS: EXAMPLE • Sorting. D is an ND problem: – – – Input: (1) a list of numbers L, and (2) a certificate c (another list) Output: Is c a sort of L? Algorithm? … Can you find a polynomial-time algorithm? If your answer is yes: Sorting. D problem is in NP-class • Is Sorting. D also a P-class problem? (C) Debasis Mitra

NON-DETERMINISIM IS NOT A MISTERY Deterministic algorithm: Traverses all nodes of the tree in worst case O : Yes [- - - ] 1 Non-deterministic algorithm: Given the certificate, it traverses only one path from root to a leaf: bounded by depth of the tree O 1: No (w=0, p=0) Opt. P=33 (w=5, p=3) Opt. P=0 O 2: Yes (w=5+3, p=33) Opt. P=0 O 3: Yes O 3: No X (w=8+8, ---) pruned (w=8, p=33) Opt. P=33, updated B =33, B == Opt. P (w=3, p=30) Opt. P=33 Opt. P is still 33 B =65 > Opt. P Pruned because Opt. P cannot be improved (w=3+8, ---) pruned B =56, but Opt. P now =56 B > Opt. P (w=3, p=30) Opt. P=33, not updated (w=8, p=56) Opt. P=56, updated Deterministic Machine versus Non-deterministic Machine (C) Debasis Mitra

CLASSIFICATION OF PROBLEMS BY COMPLEXITY (C) Debasis Mitra
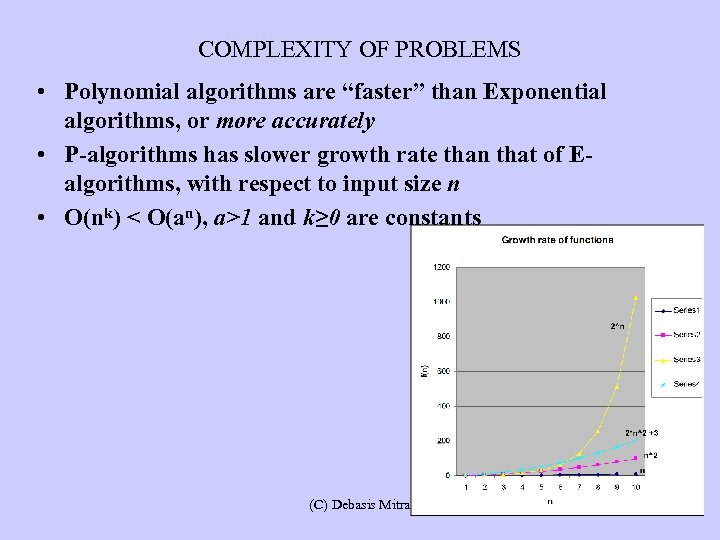
COMPLEXITY OF PROBLEMS • Polynomial algorithms are “faster” than Exponential algorithms, or more accurately • P-algorithms has slower growth rate than that of Ealgorithms, with respect to input size n • O(nk) < O(an), a>1 and k≥ 0 are constants (C) Debasis Mitra

COMPLEXITY THEORY • Each Problem has a lower bound, for Any algorithm – What is the lower bound for Comparison Sort? • Problems may be classified by such bounds • An important, but “unknown” classification would be: – Polynomial-class versus “Exponential-class” • Unfortunately: Life is much more complicated! – There is no E-class of problems (with exponential lower bounds) (C) Debasis Mitra

P-CLASS PROBLEMS AND BEYOND … • P-class of problems: which have asymptotic Polynomialtime algorithms O(nk), for k≥ 0 • There is no “E-class” of problems: No problem S may be designated as in E-class just because no polynomial algorithm for S has been found yet! • Even if you have an exponential algorithm O(an), for a>1, that does not mean a polynomial algorithm will also not exist! • We are talking about provable lower bound Ω (C) Debasis Mitra

P-CLASS PROBLEMS AND BEYOND … • Example: No polynomial algorithm for Multi-processor Last Finish Time (MPLFT) problem is found yet. – That does not mean in future a polynomial alg will not be found! – Although, it is not yet in P-class, it is not E-class either – No exponential lower bound has been found yet as well – That is all you can say about MPLFT • However, …. continued, we use some new concepts …. (C) Debasis Mitra

P VERSUS NP • Say, problem X is in P-class (read: has a polynomial algorithm) • Is X in NP-class as well? – Read : has non-deterministic Polynomial algorithm also? – Read: given a certificate, can you check it in polynomial-time? (C) Debasis Mitra

P VERSUS NP • Which one is faster? • Polynomial Alg, or Non-det polynomial alg? ≡ • What is more? • Number of nodes in the tree? or the height of the tree? [- - - ] (C) Debasis Mitra

P VERSUS NP P NP True NP-class (C) Debasis Mitra

P VERSUS NP • Say, X is in NP-class – Read: has a non-det polynomial alg • Is X in P-class as well? – Read: does it have a regular polynomial alg? [- - - ] (C) Debasis Mitra

P VERSUS NP NP P True? P-class NP-class? (C) Debasis Mitra

P VERSUS NP • P NP is True. • But is NP P also true? Meaning: NP ≡ P? • A million dollar question: http: //www. claymath. org/millennium-problems • Jury is out there: – NP ≡ P (i. e. , NP P and P NP), (C) Debasis Mitra XOR, NP ≠ P?

P VERSUS NP How would you prove: NP P not True? Or, that the truth is P NP, a proper subset NP-class X P-class (C) Debasis Mitra

P VERSUS NP LEADS TO COMPLEXITY HIERARCHY • Jury is out there: – Prove, NP P, and so, NP ≡ P? – Or, show P ≠ NP? • Did not happen yet! • But, can we find a “hardest” problem H in NP class? • And, then maybe look for a Poly-algorithm for that H? • Or, find exponential lower bound for H? • Looking for “hardest” needs some concepts on Polynomial Transformation (another new concept!!) (C) Debasis Mitra

ANOTHER NEW CONCEPT! 3. POLYNOMIAL PROBLEM-TRANSFORMATION (C) Debasis Mitra

POLYNOMIAL PROBLEM-TRANSFORMATION • How do you formally express a problem? • Problem: (Input, Output) unambiguously expressed • Problem instance: Specific values for Input, – Remember: Output is T/F in decision problems (C) Debasis Mitra

POLYNOMIAL PROBLEM-TRANSFORMATION • Problem X can be transformed to another problem Y • Problem Transformation: an algorithm – TXY (input of X) : = (input of Y) – Such that, corresponding output of X and Y are same (T/F) – TXY is an algorithm, like any other ones we have seen • WAIT TO SEE EXAMPLE! TXY Y X (C) Debasis Mitra

POLYNOMIAL PROBLEM-TRANSFORMATION • Problem Transformation: an algorithm TXY – TXY(input of X) => (input of Y) – Such that, output T/F for (input of X) = output for TXY(input X) • If there exists a TXY, and its time-complexity is Polynomial, • then X is polynomially transformed to Y TXY Y X (C) Debasis Mitra

SIGNIFICANCE OF POLYNOMIAL TRANSFORMATION • If there exists a TXY, and time-complexity of it is Polynomial, then X is polynomially transformable to Y • Suppose, Y has a polynomial algorithm Ay but, NO polynomial algorithm exists for X, YET! • However, now you can solve X by – Ay( TXY(X) ) T/F – What is the time-complexity of this dual algorithm? TXY Y: apply poly alg AY on Y X: no poly alg yet (C) Debasis Mitra X is True X is False

A CATCH IN POLYNOMIAL TRANSFORMATION • AY(TXY(X)) T/F – What is the time-complexity of this dual algorithm? • Note: |(Y output(TXY(X))| is a polynomial function of |X|, – where | | indicates problem size • Ay(Y) takes polynomial-time with respect to |Y| • But, |Y| is a polynomial of |X|, as said above • Hence: Ay(Y) above takes polynomial of polynomial-time over |X|, • Or, polynomial-time with respect to |X| (C) Debasis Mitra

SIGNIFICANCE OF POLYNOMIAL TRANSFORMATION • Ay(TXY(X)) T/F – Time-complexity of this dual algorithm is polynomial • So, X is now in P-class – Because Y was in P-class and polynomial transformation TXY is found – So, X has an indirect polynomial algorithm now • Note, this is not true in the opposite direction (C) Debasis Mitra

SIGNIFICANCE OF POLYNOMIAL TRANSFORMATION • Ay(TXY(X)) => T/F – If Ay is polynomial, then the time-complexity of this dual algorithm is also polynomial • If Y is in P-class, so is X • Y is at least as “hard” as X • Note, opposite direction is not necessarily true: – If, source problem X is already in P-class (has poly alg), – Then, polynomial transformation TXY does not say anything about the classification of target problem Y (C) Debasis Mitra

COOK-LEVIN THEOREM • All NP-class problems may be “expressed” generically as a machine: a Non-deterministic Turing Machine – Cook and Levin 1971 • https: //en. wikipedia. org/wiki/Cook%E 2%80%93 Levin _theorem • There exists a polynomial-transformation from this NDTM to the SAT problem: by an algorithm (Karp ‘ 72) (C) Debasis Mitra

C-L-K’S THEOREM SAT problem NP-class Poly-trans P-class (C) Debasis Mitra

C-L-K’S THEOREM • Find a polynomial algorithm for SAT, and win a million dollar from Clay Institute! • Then, Cook et al. ’s polynomial transformation can be used to solve any NP-class problem in polynomial-time using “your polynomial-SAT” algorithm, or P=NP • Alternatively, SAT is a good candidate for finding an exponential lower bound • Then, P ≠NP will be proved (C) Debasis Mitra

BOOLEAN SATISFIABILITY PROBLEM in PROPOSITIONAL LOGIC (SAT) (C) Debasis Mitra

“SAT” PROBLEM • Input: (U, V) – U: a set of n Boolean variables {v 1, v 2, … vn}(value: T, F) – V: a conjunctive normal formula (CNF) over U – Conjunctive normal formula is conjunction of disjunctions: { (. v. v. ) ^ (. v. v. v. ) ^ …} • Output: Does there exist a satisfiable assignment to make C True? ≡ can you find values of U such that V becomes True? • V: expressed as a set of m Clauses {C 1, C 2, … Cm} • Ci: is a list (disjunction) of literals (a variable, or its negation) • What is the complexity of finding above output? (C) Debasis Mitra

EXAMPLE: SAT PROBLEM • Input: (U, V) – U: {a, b, c, d} – V: {{a, b, c}, {a, d}, {~b, ~d}}, ~ indicates NOT – in CNF: (a V b V c) ˄ (a V d) ˄ (~b V ~d) • Output: Does there exist a satisfiable assignment to make V True? • Answer: Yes – A=T, b=F, c=? , d=? , – question-mark ? means “don’t care” or T and F both correct • What is the complexity of answering the above question? (C) Debasis Mitra

SAT is in WHICH-CLASS? • Input: (U, V) – U: {a, b, c, d} – V: {{a, b, c}, {a, d}, {~b, ~d}} – a certificate: (a=F, b=T, c=T, d=T) • Output: Is the certificate a satisfiable assignment to make V True? • Answer: No – C 1 = T, C 2 = T, C 3 = F – V = False • What is the complexity of answering the above question? (C) Debasis Mitra

SAT is in NP-CLASS • Input: (U, V) – U: {a, b, c, d} – V: {{a, b, c}, {a, d}, {~b, ~d}} – a certificate: (a=F, b=T, c=T, d=T) • Output: Is the certificate a satisfiable assignment to make V True? • Answer: No – C 1 = T, C 2 = T, C 3 = F: makes V = False • Complexity: O(nm) • So, SAT is in NP-class • But not in P-class, “yet”: no one found a polynomial alg (C) Debasis Mitra

C-L-K’S THEOREM: SAT IS NP-HARD • Polynomial Transformation from NDTM to SAT • SAT is NP-hard • Either find a polynomial algorithm for SAT: then P=NP • Or, find exponential lower bound for SAT: then P≠NP (C) Debasis Mitra

C-L-K’S THEOREM: SAT IS NP-COMPLETE • Polynomial Transformation from NDTM to SAT • SAT is NP-hard • NP-hard: poly-trans from NDTM • NP-complete: NP-hard & NP-class • SAT is NP-class => SAT is NP-complete (C) Debasis Mitra
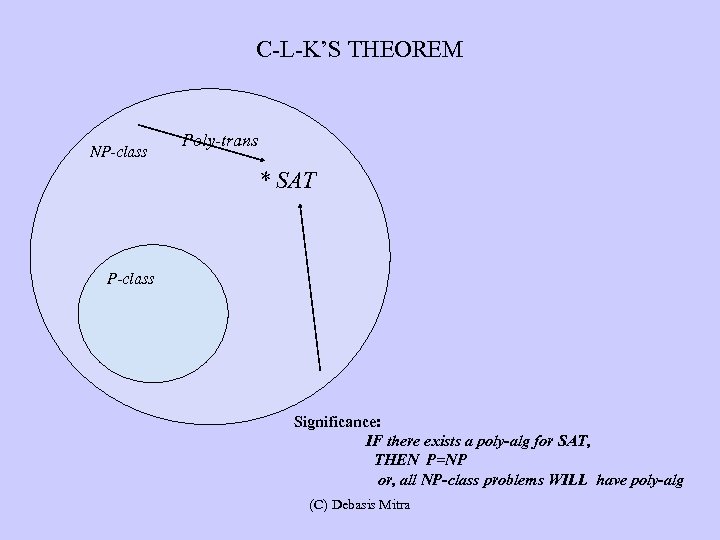
C-L-K’S THEOREM NP-class Poly-trans * SAT P-class Significance: IF there exists a poly-alg for SAT, THEN P=NP or, all NP-class problems WILL have poly-alg (C) Debasis Mitra

C-L-K’S MORE RESULT: 3 -SAT IS NP-HARD • Polynomial Transformation from SAT to 3 -SAT • Significance: IF there exists a polynomial alg for 3 -SAT, Then, SAT would have an indirect poly-alg, So, P=NP would be true, or, all NP-class problems WOULD have poly-algs • Polynomial Transforms are Transitive – A B, and B C, implies A C • Chain of poly-transformation creates NP-hard class (C) Debasis Mitra
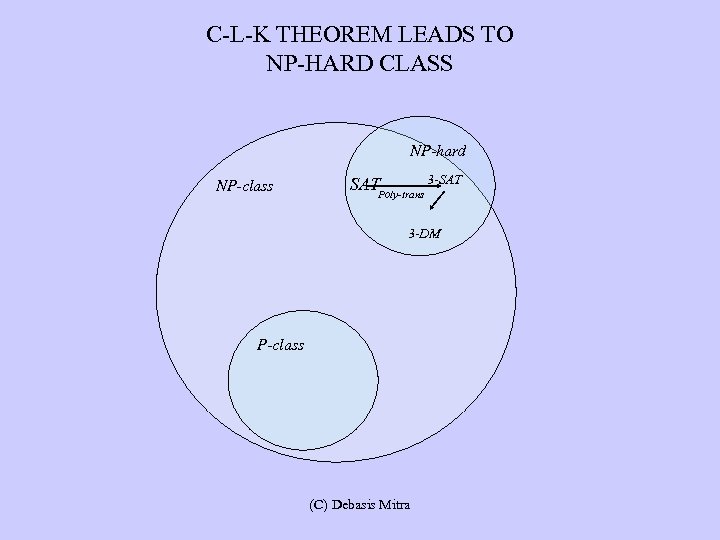
C-L-K THEOREM LEADS TO NP-HARD CLASS NP-hard NP-class SATPoly-trans 3 -SAT 3 -DM P-class (C) Debasis Mitra

C-L-K THEOREM LEADS TO NP-COMPLETE CLASS NP NP-hard = NP-complete NP-class NP-complete SAT 3 -SAT Poly-trans 3 -DM P-class (C) Debasis Mitra

C-L-K’S MORE RESULTS: 3 -SAT IS NP-HARD • Chain of poly-transformation creates NP-hard class • Any poly-alg found for a problem in NP-hard will solve P=NP question (for “yes”) • Overlap of NP-hard and NP-class makes NP-complete • NP-class problem has an exponential alg. O(an), and • So, is any NP-complete problem – Branching factor of decision tree is bounded by a constant a (C) Debasis Mitra
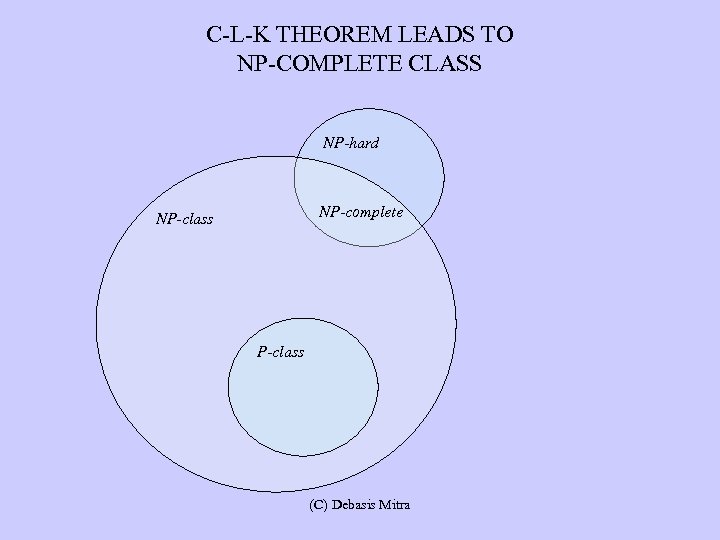
C-L-K THEOREM LEADS TO NP-COMPLETE CLASS NP-hard NP-complete NP-class (C) Debasis Mitra

WHAT IS 3 -SAT? • SAT with limit on clause-size ≤ 3 • Input: (U, V) – U: {a, b, c, d} – V: {{a, b, c}, {a, d}, {~b, ~d}} • This is 3 -SAT ok • We will use clause size = 3, rather than ≤ 3 (C) Debasis Mitra

3 -SAT IS NP-HARD • Theorem: There exists a poly-trans from SAT to 3 -SAT • TXY: • Given ANY given SAT input, you can create a size-fixed set of clauses, – by introducing new variables and clauses, • … such that, T/F of the <input SAT> is preserved! • And you can do that in polynomial time with respect to SAT’s input size • However, • 2 -SAT is in P-class: David-Putnam poly algorithm – You cannot find a polynomial-trans from SAT to 2 -SAT! (C) Debasis Mitra

3 -SAT IS NP-HARD • Classify SAT clauses into 4 groups: 1 -clauses, 2 -clauses, 3 -clauses, and p-clauses with p>3 literals in these clauses • We will (1) show transformations (to the corresponding 3 -clauses) for each of these 4 types of clauses • (2) prove that the transformations are correct, i. e. , truth preserving; and then • (3) we will discuss the polynomial-time nature of the aggregate-transformation at the end (C) Debasis Mitra

3 -SAT IS NP-HARD For each clause do Input SAT clause-type Input SATclause Output 3 SAT Output 3 clause SAT new variables For each 1 clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} u is a literal New variables for each such 1 -clause: z 1, z 2, WHY? Remember: 3 clauses are created, and 2 NEW variables added in target 3 -SAT for EACH 1 -clause in the source SAT (C) Debasis Mitra

3 -SAT IS NP-HARD For each clause do Input SAT clause-type Input SATclause Output 3 SAT Output 3 clause SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} New variable for each such clause: z 1 u 1, u 2 are literals Target: 2 clauses created, and 1 new variable added Source: for each 2 -clause (C) Debasis Mitra
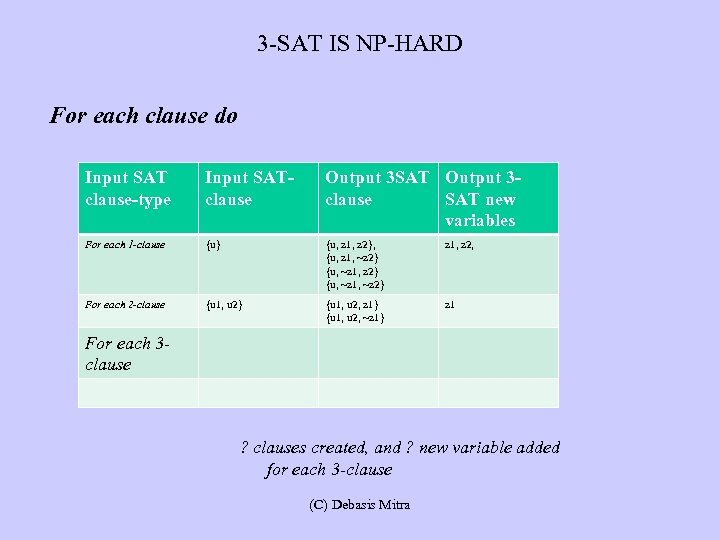
3 -SAT IS NP-HARD For each clause do Input SAT clause-type Input SATclause Output 3 SAT Output 3 clause SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 -clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} z 1 For each 3 clause ? clauses created, and ? new variable added for each 3 -clause (C) Debasis Mitra
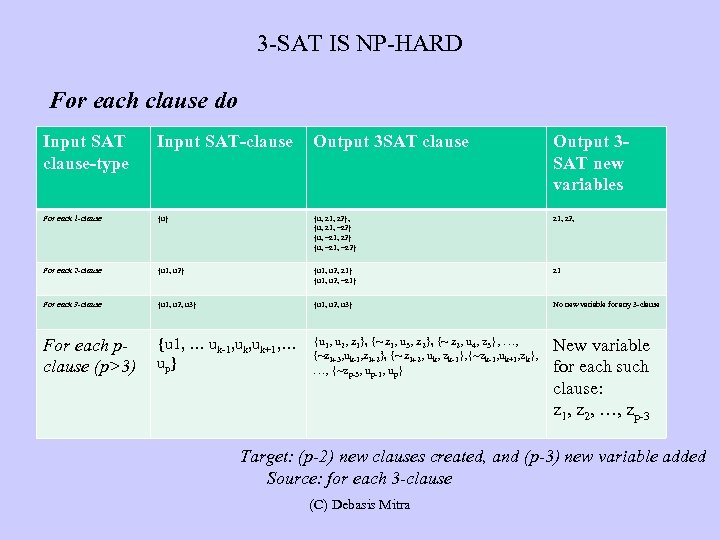
3 -SAT IS NP-HARD For each clause do Input SAT clause-type Input SAT-clause Output 3 SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 -clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} z 1 For each 3 -clause {u 1, u 2, u 3} No new variable for any 3 -clause For each pclause (p>3) {u 1, … uk-1, uk+1, … up} {u 1, u 2, z 1}, {~ z 1, u 3, z 2}, {~ z 2, u 4, z 3}, …, {~zk-3, uk-1, zk-2}, {~ zk-2, uk, zk-1}, {~zk-1, uk+1, zk}, …, {~zp-3, up-1, up} New variable for each such clause: z 1, z 2, …, zp-3 Target: (p-2) new clauses created, and (p-3) new variable added Source: for each 3 -clause (C) Debasis Mitra
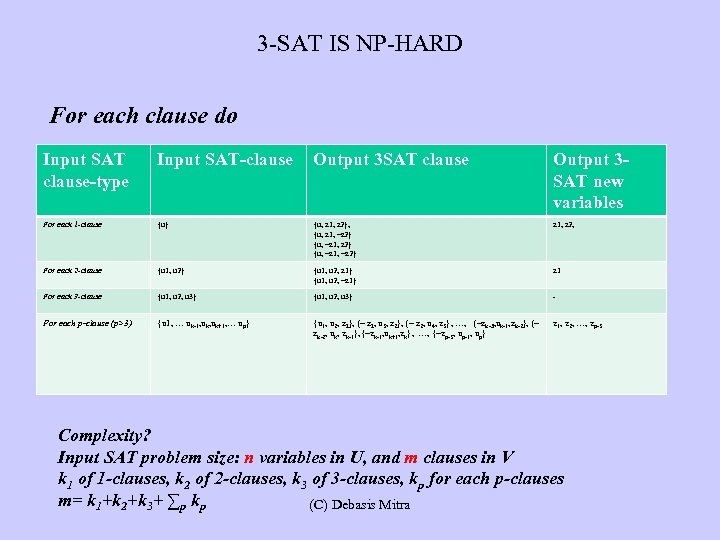
3 -SAT IS NP-HARD For each clause do Input SAT clause-type Input SAT-clause Output 3 SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 -clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} z 1 For each 3 -clause {u 1, u 2, u 3} - For each p-clause (p>3) {u 1, … uk-1, uk+1, … up} {u 1, u 2, z 1}, {~ z 1, u 3, z 2}, {~ z 2, u 4, z 3}, …, {~zk-3, uk-1, zk-2}, {~ zk-2, uk, zk-1}, {~zk-1, uk+1, zk}, …, {~zp-3, up-1, up} z 1, z 2, …, zp-3 Complexity? Input SAT problem size: n variables in U, and m clauses in V k 1 of 1 -clauses, k 2 of 2 -clauses, k 3 of 3 -clauses, kp for each p-clauses m= k 1+k 2+k 3+ ∑p kp (C) Debasis Mitra
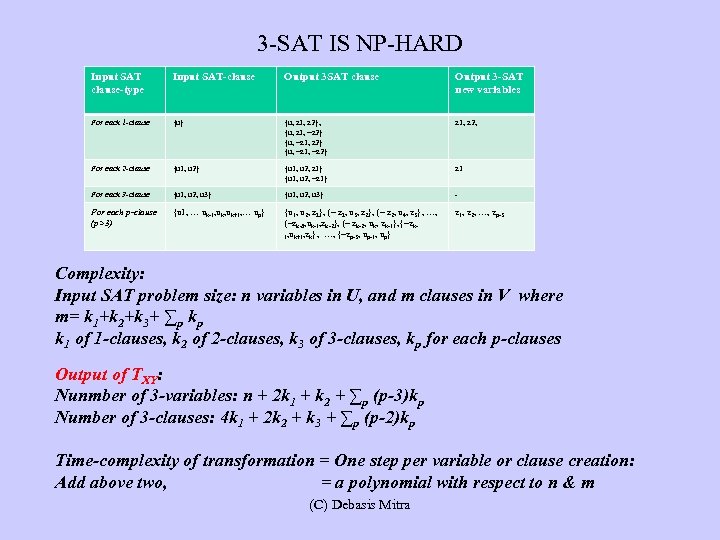
3 -SAT IS NP-HARD Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 -clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} z 1 For each 3 -clause {u 1, u 2, u 3} - For each p-clause (p>3) {u 1, … uk-1, uk+1, … up} {u 1, u 2, z 1}, {~ z 1, u 3, z 2}, {~ z 2, u 4, z 3}, …, {~zk-3, uk-1, zk-2}, {~ zk-2, uk, zk-1}, {~zk 1, uk+1, zk}, …, {~zp-3, up-1, up} z 1, z 2, …, zp-3 Complexity: Input SAT problem size: n variables in U, and m clauses in V where m= k 1+k 2+k 3+ ∑p kp k 1 of 1 -clauses, k 2 of 2 -clauses, k 3 of 3 -clauses, kp for each p-clauses Output of TXY: Nunmber of 3 -variables: n + 2 k 1 + k 2 + ∑p (p-3)kp Number of 3 -clauses: 4 k 1 + 2 k 2 + k 3 + ∑p (p-2)kp Time-complexity of transformation = One step per variable or clause creation: Add above two, = a polynomial with respect to n & m (C) Debasis Mitra

Is 3 -SAT also NP-complete? • Trivial, SAT is in NP-class, so is 3 -SAT: • 3 -SAT is a set of 3 -clauses over a set of Boolean variables • Certificate is a given value for each variable. • In O(nm) time the clauses may be checked for satisfiability Þ 3 -SAT is NP • We already proved 3 -SAT is NP-hard • => 3 -SAT is NP-complete (C) Debasis Mitra
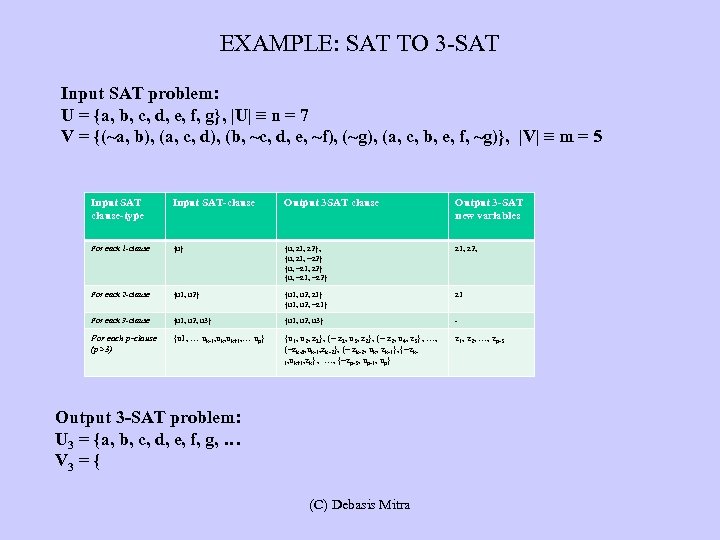
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 -clause {u} {u, z 1, z 2}, {u, z 1, ~z 2} {u, ~z 1, ~z 2} z 1, z 2, For each 2 -clause {u 1, u 2} {u 1, u 2, z 1} {u 1, u 2, ~z 1} z 1 For each 3 -clause {u 1, u 2, u 3} - For each p-clause (p>3) {u 1, … uk-1, uk+1, … up} {u 1, u 2, z 1}, {~ z 1, u 3, z 2}, {~ z 2, u 4, z 3}, …, {~zk-3, uk-1, zk-2}, {~ zk-2, uk, zk-1}, {~zk 1, uk+1, zk}, …, {~zp-3, up-1, up} z 1, z 2, …, zp-3 Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, … V 3 = { (C) Debasis Mitra
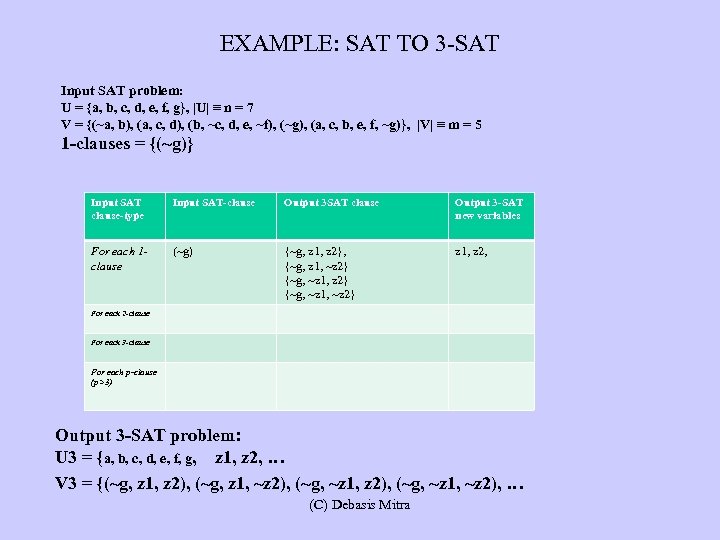
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 1 -clauses = {(~g)} Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 clause (~g) {~g, z 1, z 2}, {~g, z 1, ~z 2} {~g, ~z 1, ~z 2} z 1, z 2, For each 2 -clause For each 3 -clause For each p-clause (p>3) Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, z 1, z 2, … V 3 = {(~g, z 1, z 2), (~g, z 1, ~z 2), (~g, ~z 1, ~z 2), … (C) Debasis Mitra
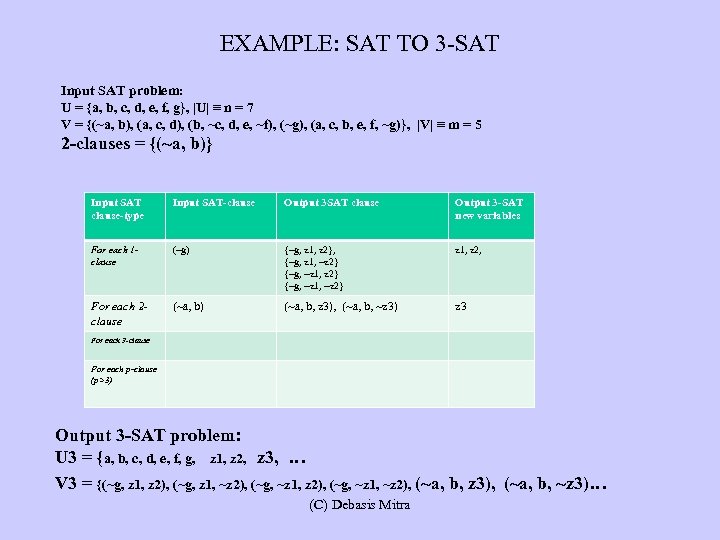
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 2 -clauses = {(~a, b)} Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 clause (~g) {~g, z 1, z 2}, {~g, z 1, ~z 2} {~g, ~z 1, ~z 2} z 1, z 2, For each 2 clause (~a, b) (~a, b, z 3), (~a, b, ~z 3) z 3 For each 3 -clause For each p-clause (p>3) Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, z 1, z 2, z 3, … V 3 = {(~g, z 1, z 2), (~g, z 1, ~z 2), (~g, ~z 1, ~z 2), (~a, b, z 3), (~a, b, ~z 3)… (C) Debasis Mitra
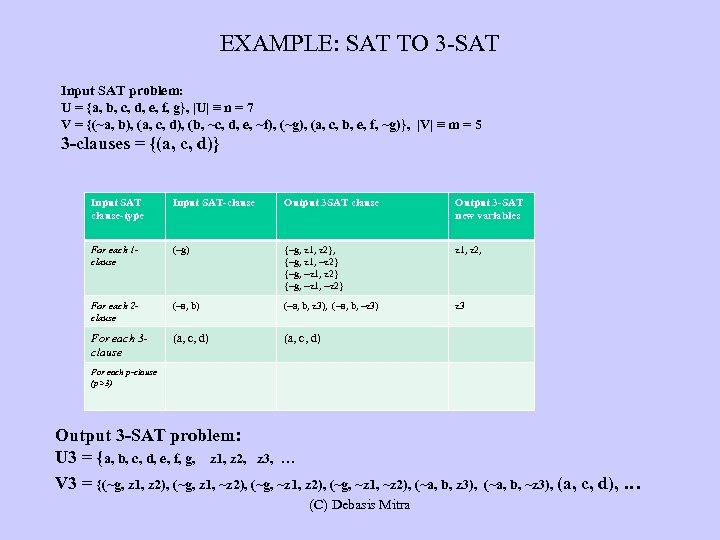
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 3 -clauses = {(a, c, d)} Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 clause (~g) {~g, z 1, z 2}, {~g, z 1, ~z 2} {~g, ~z 1, ~z 2} z 1, z 2, For each 2 clause (~a, b) (~a, b, z 3), (~a, b, ~z 3) z 3 For each 3 clause (a, c, d) For each p-clause (p>3) Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, z 1, z 2, z 3, … V 3 = {(~g, z 1, z 2), (~g, z 1, ~z 2), (~g, ~z 1, ~z 2), (~a, b, z 3), (C) Debasis Mitra (~a, b, ~z 3), (a, c, d), …
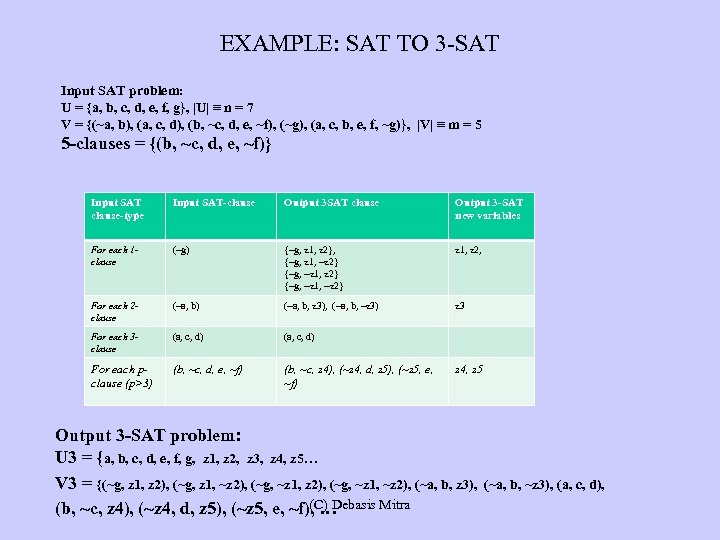
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 5 -clauses = {(b, ~c, d, e, ~f)} Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 clause (~g) {~g, z 1, z 2}, {~g, z 1, ~z 2} {~g, ~z 1, ~z 2} z 1, z 2, For each 2 clause (~a, b) (~a, b, z 3), (~a, b, ~z 3) z 3 For each 3 clause (a, c, d) For each pclause (p>3) (b, ~c, d, e, ~f) (b, ~c, z 4), (~z 4, d, z 5), (~z 5, e, ~f) z 4, z 5 Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, z 1, z 2, z 3, z 4, z 5… V 3 = {(~g, z 1, z 2), (~g, z 1, ~z 2), (~g, ~z 1, ~z 2), (~a, b, z 3), (C) Debasis Mitra (b, ~c, z 4), (~z 4, d, z 5), (~z 5, e, ~f), … (~a, b, ~z 3), (a, c, d),
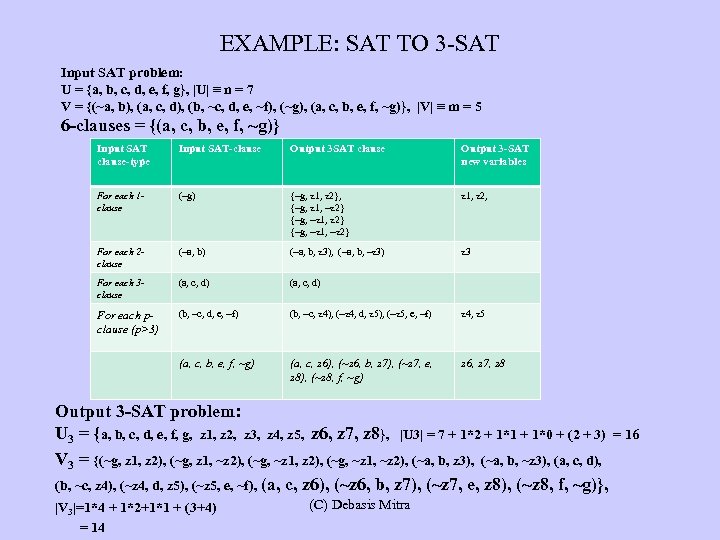
EXAMPLE: SAT TO 3 -SAT Input SAT problem: U = {a, b, c, d, e, f, g}, |U| ≡ n = 7 V = {(~a, b), (a, c, d), (b, ~c, d, e, ~f), (~g), (a, c, b, e, f, ~g)}, |V| ≡ m = 5 6 -clauses = {(a, c, b, e, f, ~g)} Input SAT clause-type Input SAT-clause Output 3 SAT clause Output 3 -SAT new variables For each 1 clause (~g) {~g, z 1, z 2}, {~g, z 1, ~z 2} {~g, ~z 1, ~z 2} z 1, z 2, For each 2 clause (~a, b) (~a, b, z 3), (~a, b, ~z 3) z 3 For each 3 clause (a, c, d) For each pclause (p>3) (b, ~c, d, e, ~f) (b, ~c, z 4), (~z 4, d, z 5), (~z 5, e, ~f) z 4, z 5 (a, c, b, e, f, ~g) (a, c, z 6), (~z 6, b, z 7), (~z 7, e, z 8), (~z 8, f, ~g) z 6, z 7, z 8 Output 3 -SAT problem: U 3 = {a, b, c, d, e, f, g, z 1, z 2, z 3, z 4, z 5, z 6, z 7, z 8}, |U 3| = 7 + 1*2 + 1*1 + 1*0 + (2 + 3) = 16 V 3 = {(~g, z 1, z 2), (~g, z 1, ~z 2), (~g, ~z 1, ~z 2), (~a, b, z 3), (~a, b, ~z 3), (a, c, d), (b, ~c, z 4), (~z 4, d, z 5), (~z 5, e, ~f), (a, c, z 6), (~z 6, b, z 7), (~z 7, e, z 8), (~z 8, f, ~g)}, |V 3|=1*4 + 1*2+1*1 + (3+4) = 14 (C) Debasis Mitra

SUMMARY ON COMPLEXITY P-class problem Polynomial algorithm exists NP-class problem Certificate checking in polynomial. Must have exponential algorithm. P in NP? Yes. Poly-alg for original indicates poly-alg for certificate checking. NP in P? Not known. Polynomial transformation. X to Y poly-trans means X can be solved by solving Y. If Y is in P, then so is X. (C) Debasis Mitra

SUMMARY ON COMPLEXITY NP-hard All NP-class problems can be poly-transformed to any NP-hard problem NP-complete NP-hard and NP-class When to prove a problem Y is NP-complete? Intuition tells so. How to prove Y is NPcomplete? (a) Find a poly-trans from an NP-hard problem X to Y: - (1) truth-preserving, and (2) poly-time. & (b) Prove Y is NP-class. Any other way to prove Y is NP- Yes, many. E. g. prove a restricted version of Y is an hard? NP-hard problem. Not the other way round: 2 -SAT is P-class. https: //en. wikipedia. org/wiki/DPLL_algorithm is poly -time for 2 -SAT A poly-alg is found for an NPhard problem (by a nut/ a genius!). What would that mean? (1) Not truth preserving, or (2) not poly-trans, or (3) source problem (X) was not really NP-hard, or, Wrong proof. Otherwise, (3) NP=P is just being proved! (C) Debasis Mitra

SUMMARY ON COMPLEXITY Examples of NP-complete problems: 1. 0 -1 Knapsack decision problem 2. Multi-processor Last-time-finish scheduling problem 3. Hamiltonian Circuit decision problem: Given a graph G, does there exists a cycle involving each node once and only once? [“Does there exist a cycle in G involving each arc once and only once? ” Euler circuit problem: P-class] 4. 3 dimensional matching (3 DM): Given three equal size sets X, Y, Z of three types, does there exists a perfect matching? Matching set: A, a set of 3 elements (marriage), one from each of X, Y, and Z. Perfect matching (subset of A): each element of X, Y, Z appears in one and only one marriage in A. [2 DM is P-class, but 3 DM is NP-complete] (C) Debasis Mitra

HOW TO DEAL WITH NP-COMPLETE PROBLEM Y is proved NP-complete Restrict Y to something Z, then see if poly-alg may be developed for Z SAT to 2 -SAT Approximate solution for Y e. g. Multi-processor LFT scheduling may be acceptable problem A pseudo-poly alg may 0 -1 Knapsack Dynamic Programming work most of the time for Y Apply pruning in Branchand-bound exponentialtime alg for Y We use such smart exp algorithms for most NP-complete problems. Do not care about the worst-case complexity, that is still exponential! NP-complete problems have additional inherent structures! How about parallel computing? Does not solve an NP-comp problem in poly-time (C) Debasis Mitra

MORE ON COMPLEXITY ISSUES Co-NP Complementary to NP-class. Overlaps NP Co-NP complete Poly trans from all Co-NP, and inside Co. NP P-space Remember, space complexity is less than or equal to time complexity! P-space complete Harder than NP-complete. Infinite hierarchy… Quantum computinghierarchy Inherently Non-deterministic computing model, but has its own hierarchy. Some NP-complete problems (TSP) do get solved in poly-time (non-deterministically) Undecidable problem Definition: No halting Turing machine exists, i. e. No algorithm exists in general. This is NOT about complexity! (C) Debasis Mitra
a6e88c913bbfcc0c7de3fb5ff04d9aec.ppt