These slides are provided as a teaching support

These slides are provided as a teaching support for the community. They can be freely modified and used as far as the original authors (T. Schiex and J. Larrosa) contribution is clearly mentionned and visible and that any modification is acknowledged by the author of the modification. Soft constraint processing Javier Larrosa UPC – Barcelona Spain September 2006 Thomas Schiex INRA – Toulouse France CP 06

Overview 1. Frameworks n 2. Algorithms n n 3. Generic and specific Search: complete and incomplete Inference: complete and incomplete Integration with CP n n Soft as hard Soft as global constraint September 2006 CP 06 2

Parallel mini-tutorial o CSP SAT strong relation Along the presentation, we will highlight the connections with SAT o Multimedia trick: o n SAT slides in yellow background September 2006 CP 06 3

Why soft constraints? o o o CSP framework: natural for decision problems SAT framework: natural for decision problems with boolean variables Many problems are constrained optimization problems and the difficulty is in the optimization part September 2006 CP 06 4

Why soft constraints? q Earth Observation Satellite Scheduling n n September 2006 Given a set of requested pictures (of different importance)… … select the best subset of compatible pictures … … subject to available resources: o 3 on-board cameras o Data-bus bandwith, setup-times, orbiting Best = maximize sum of importance CP 06 5

Why soft constraints? o Frequency assignment n n n Given a telecommunication network …find the best frequency for each communication link avoiding interferences Best can be: o o September 2006 Minimize the maximum frequency (max) Minimize the global interference (sum) CP 06 6

Why soft constraints? o Combinatorial auctions n Given a set G of goods and a set B of bids… o n n Bid (bi, vi), bi requested goods, vi value … find the best subset of compatible bids Best = maximize revenue (sum) b 3 v 3 G 5 G 2 b 1 v 1 G 7 G 6 G 3 G 8 G 4 b 4 v 4 b 2 v 2 September 2006 CP 06 7

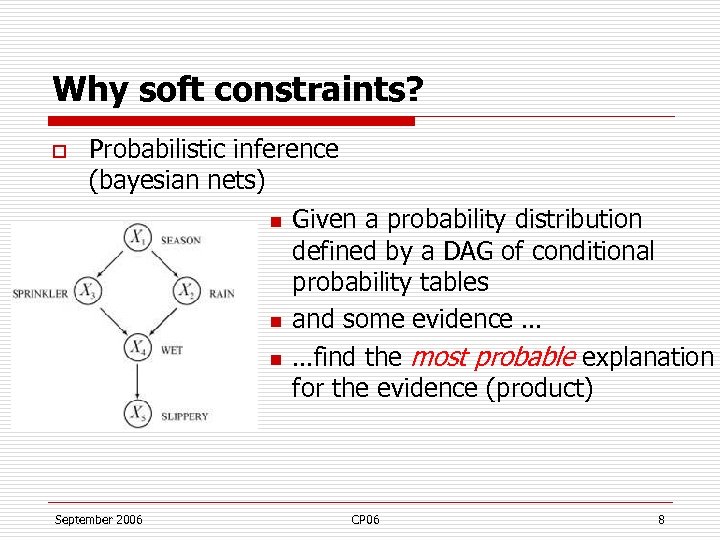Why soft constraints? o Probabilistic inference (bayesian nets) n n n September 2006 Given a probability distribution defined by a DAG of conditional probability tables and some evidence … …find the most probable explanation for the evidence (product) CP 06 8

Why soft constraints? o Even in decision problems: n users may have preferences among solutions Experiment: give users a few solutions and they will find reasons to prefer some of them. September 2006 CP 06 9

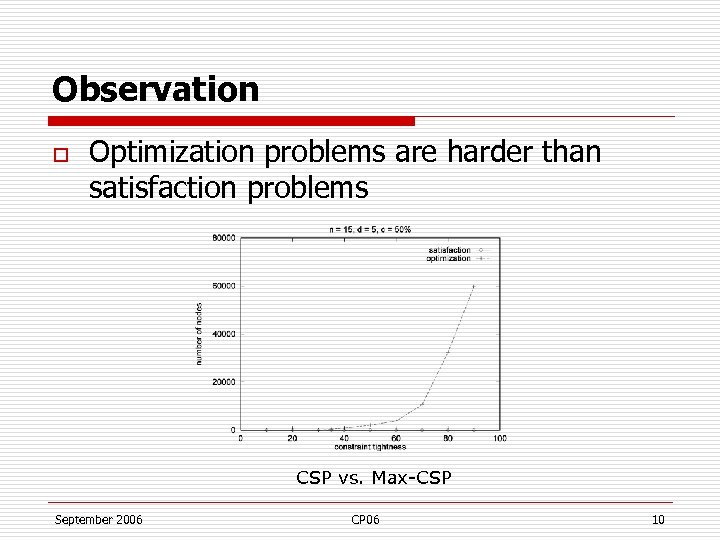Observation o Optimization problems are harder than satisfaction problems CSP vs. Max-CSP September 2006 CP 06 10

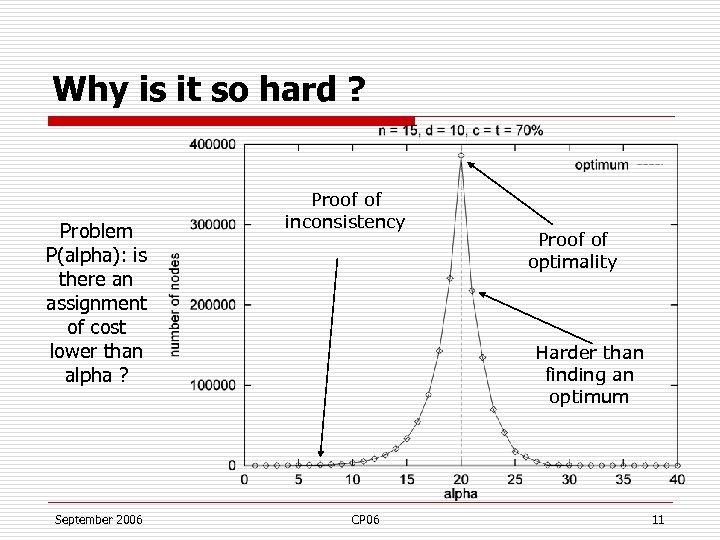Why is it so hard ? Problem P(alpha): is there an assignment of cost lower than alpha ? September 2006 Proof of inconsistency Proof of optimality Harder than finding an optimum CP 06 11

Notation o X={x 1, . . . , xn} variables (n variables) D={D 1, . . . , Dn} finite domains (max size d) o Z⊆Y⊆X, o n n t. Y[Z] t. Y[-x] = t. Y[Y-{x}] f. Y: ∏xi∊Y Di E September 2006 is a tuple on Y is its projection on Z is projecting out variable x is a cost function on Y CP 06 12

Generic and specific frameworks Valued CN Semiring CN September 2006 weighted CN fuzzy CN … CP 06

Costs (preferences) o E costs (preferences) set n n o o ordered by ≼ if a ≼ b then a is better than b Costs are associated to tuples Combined with a dedicated operator n n n max: priorities Fuzzy/possibilistic CN +: additive costs *: factorized probabilities… September 2006 CP 06 Weighted CN Probabilistic CN, BN 14

Soft constraint network (CN) o (X, D, C) n n n o o o X={x 1, . . . , xn} variables D={D 1, . . . , Dn} finite domains identity C={f, . . . } cost functions anihilator o f. S, fij, fi f∅ scope S, {xi, xj}, {xi}, ∅ o f. S(t): E (ordered by ≼, ≼T) Obj. Function: F(X)= f. S (X[S]) Solution: F(t) T Task: find optimal solution September 2006 CP 06 • commutative • associative • monotonic 15

Specific frameworks E ≼T Classic CN {t, f} and t ≼f Possibilistic [0, 1] max 0≼ 1 Fuzzy CN [0, 1] max≼ 1≼ 0 Weighted CN [0, k] + 0≼k Bayes net [0, 1] × 1≼ 0 Instance September 2006 CP 06 16

Weighted Clauses o (C, w) n n weighted clause C w disjunction of literals cost of violation n (ordered by ≼, ≼T) n o w E combinator of costs Cost functions = weighted clauses xi xj f(xi, xj) 0 0 6 0 1 0 2 1 1 3 September 2006 (xi ν xj, 6), (¬xi ν xj, 2), (¬xi ν ¬xj, 3) CP 06 17

Soft CNF formula o F={(C, w), …} Set of weighted clauses o o o mandatory clause o o (C, T) (C, w

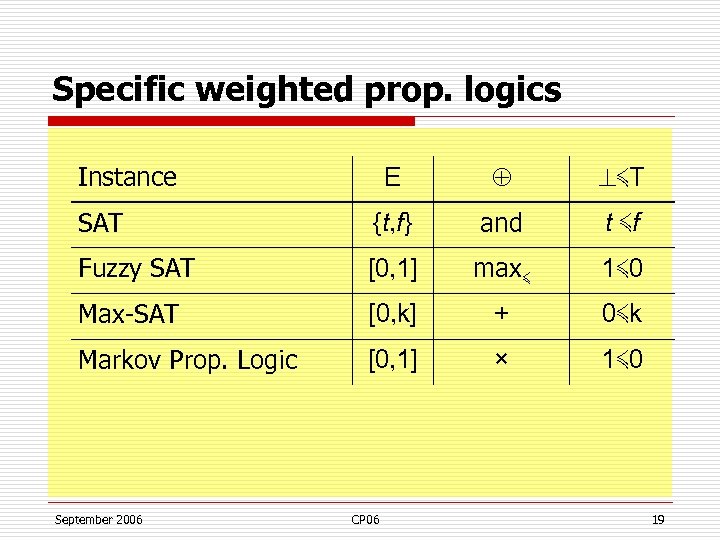Specific weighted prop. logics E ≼T SAT {t, f} and t ≼f Fuzzy SAT [0, 1] max≼ 1≼ 0 Max-SAT [0, k] + 0≼k Markov Prop. Logic [0, 1] × 1≼ 0 Instance September 2006 CP 06 19

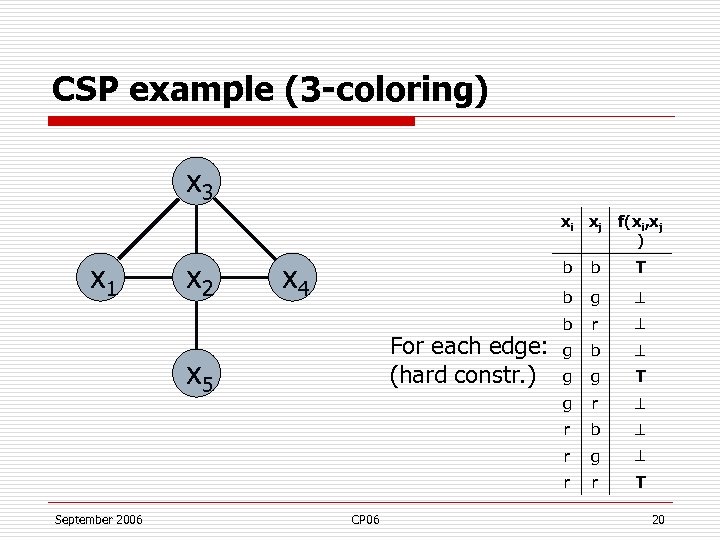CSP example (3 -coloring) x 3 xi xj x 1 x 2 x 4 f(xi, xj ) b b r g b g g T r b r g r CP 06 r September 2006 g g x 5 T b For each edge: (hard constr. ) b r T 20

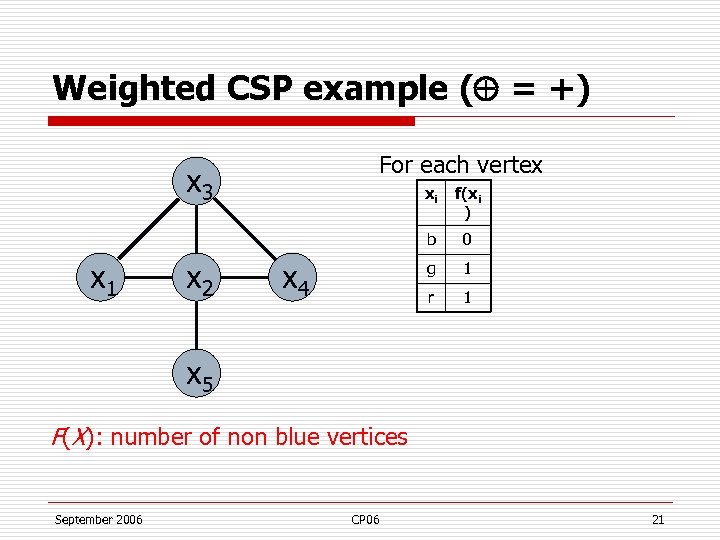Weighted CSP example ( = +) For each vertex x 3 x 2 0 g 1 r x 4 f(xi ) b x 1 xi 1 x 5 F(X): number of non blue vertices September 2006 CP 06 21

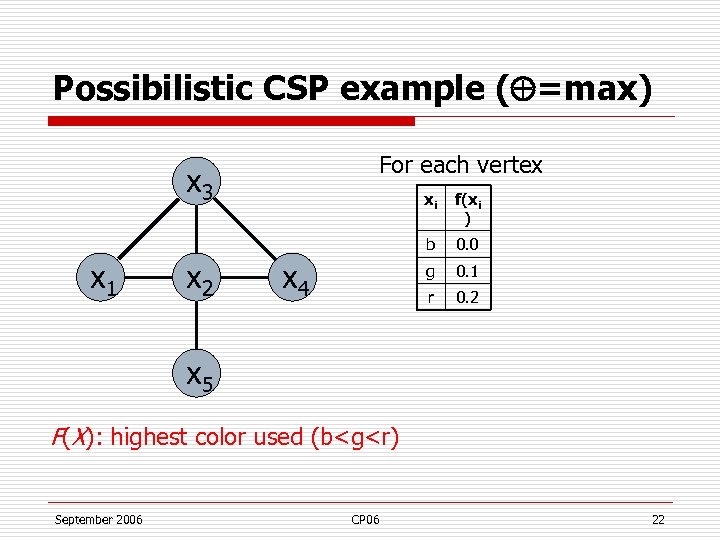Possibilistic CSP example ( =max) For each vertex x 3 x 2 0. 0 g 0. 1 r x 4 f(xi ) b x 1 xi 0. 2 x 5 F(X): highest color used (b

Some important details o o T = maximum acceptable violation. Empty scope soft constraint f (a constant) n n Gives an obvious lower bound on the optimum If you do not like it: f = Additional expression power September 2006 CP 06 23

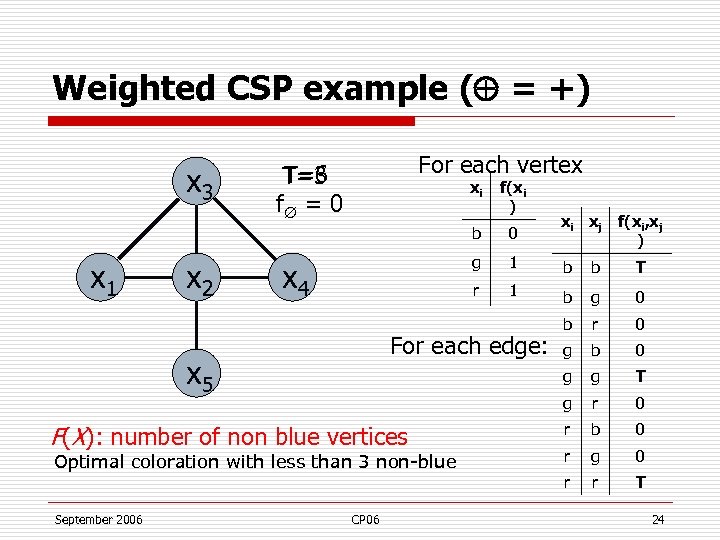Weighted CSP example ( = +) x 3 For each vertex T=6 T=3 f = 0 x 2 1 b b T r 1 b g 0 b r 0 g b 0 g g T g r 0 r b 0 r g 0 r r T For each edge: x 5 F(X): number of non blue vertices Optimal coloration with less than 3 non-blue September 2006 0 g x 4 f(xi ) b x 1 xi CP 06 xi xj f(xi, xj ) 24

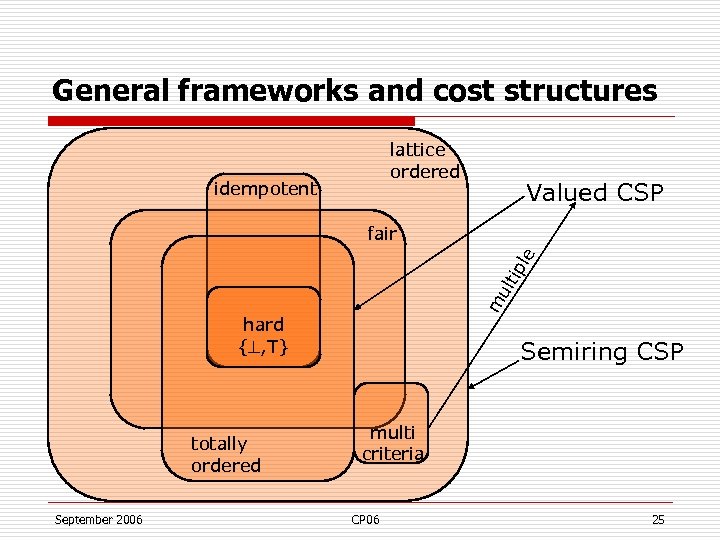General frameworks and cost structures lattice ordered idempotent Valued CSP m ult ipl e fair hard { , T} totally ordered September 2006 Semiring CSP multi criteria CP 06 25

Idempotency a a = a (for any a) For any f. S implied by (X, D, C) ≡ (X, D, C∪{f. S}) n n Classic CN: Possibilistic CN: Fuzzy CN: … September 2006 = and = max≼ CP 06 26

Fairness o Ability to compensate for cost increases by subtraction using a pseudo-difference: For b ≼ a, (a ⊖ b) b = a n n n Classic CN: Fuzzy CN: Weighted CN: Bayes nets: … September 2006 a⊖b = or (max) a⊖b = max≼ a⊖b = a-b (a≠T) else T a⊖b = / CP 06 27

Processing Soft constraints Search complete (systematic) incomplete (local) Inference complete (variable elimination) incomplete (local consistency) September 2006 CP 06

Systematic search Branch and bound(s) September 2006 CP 06

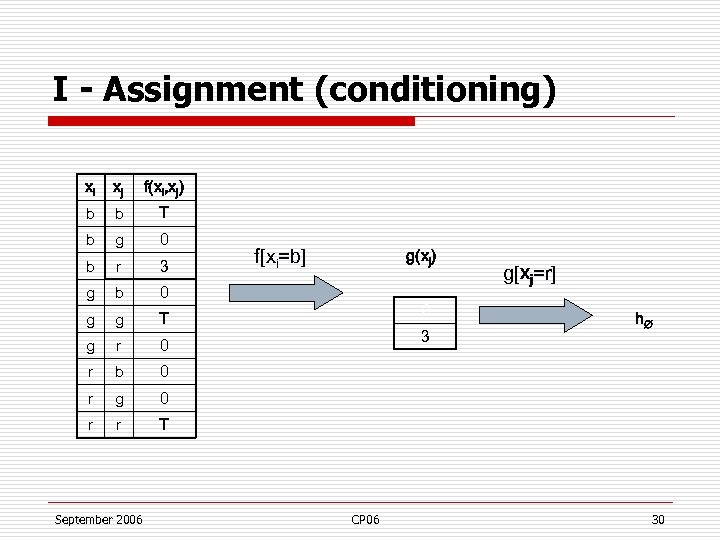I - Assignment (conditioning) xi xj f(xi, xj) b b T b g 0 b r 3 g b 0 g g T g r 0 r b 0 r g 0 r r T September 2006 f[xi=b] g(xj) 0 3 CP 06 g[xj=r] h 30

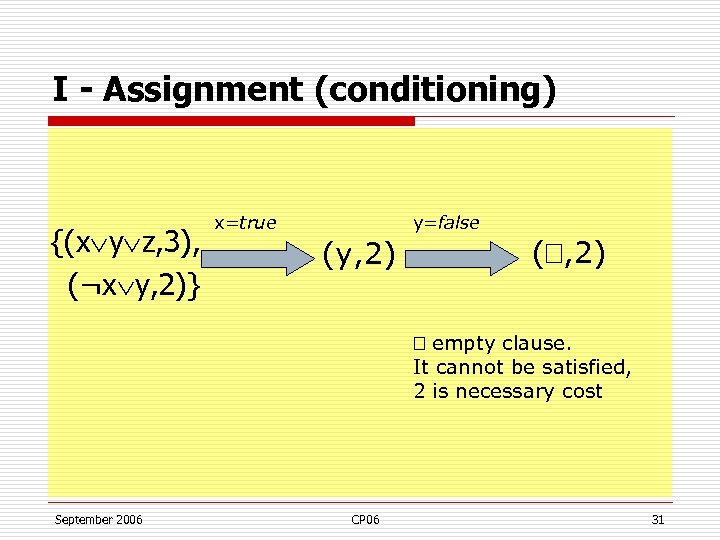I - Assignment (conditioning) {(x y z, 3), (¬x y, 2)} x=true y=false (y, 2) ( , 2) empty clause. It cannot be satisfied, 2 is necessary cost September 2006 CP 06 31

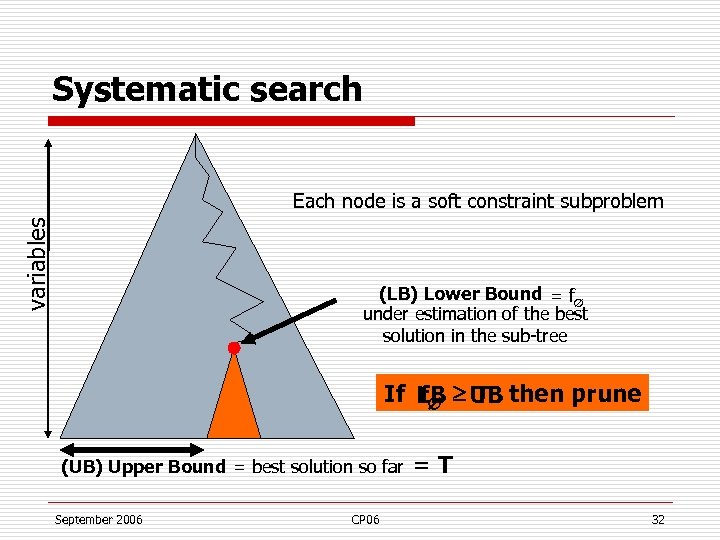Systematic search variables Each node is a soft constraint subproblem (LB) Lower Bound = f under estimation of the best solution in the sub-tree If LB UB then prune f T (UB) Upper Bound = best solution so far September 2006 CP 06 = T 32

Improving the lower bound (WCSP) o o o Sum up costs that will necessarily occur (no matter what values are assigned to the variables) PFC-DAC (Wallace et al. 1994) PFC-MRDAC (Larrosa et al. 1999…) Russian Doll Search (Verfaillie et al. 1996) Mini-buckets (Dechter et al. 1998) September 2006 CP 06 34

Improving the lower bound (Max-SAT) o o o Detect independent subsets of mutually inconsistent clauses LB 4 a (Shen and Zhang, 2004) UP (Li et al, 2005) Max Solver (Xing and Zhang, 2005) Max. Satz (Li et al, 2006) … September 2006 CP 06 35

Local search Nothing really specific September 2006 CP 06

Local search Based on perturbation of solutions in a local neighborhood o o o o Simulated annealing Tabu search Variable neighborhood search Greedy rand. adapt. search (GRASP) Evolutionary computation (GA) Ant colony optimization… For boolean variables: • GSAT • … See: Blum & Roli, ACM comp. surveys, 35(3), 2003 September 2006 CP 06 37

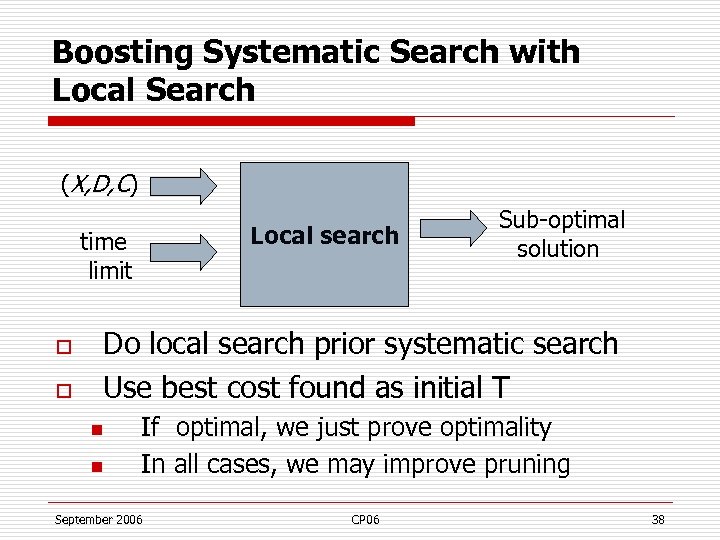Boosting Systematic Search with Local Search (X, D, C) time limit o o Local search Sub-optimal solution Do local search prior systematic search Use best cost found as initial T n n If optimal, we just prove optimality In all cases, we may improve pruning September 2006 CP 06 38

Boosting Systematic Search with Local Search o Ex: Frequency assignment problem n Instance: CELAR 6 -sub 4 o n n n #var: 22 , #val: 44 , Optimum: 3230 Solver: toolbar 2. 2 with default options T initialized to 100000 3 hours T initialized to 3230 1 hour o Optimized local search can find the optimum in a less than 30” (incop) September 2006 CP 06 39

Complete inference Variable (bucket) elimination Graph structural parameters September 2006 CP 06

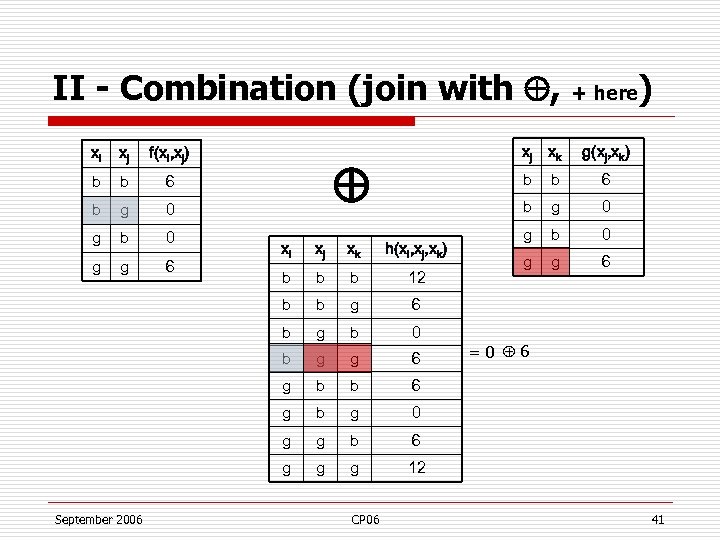II - Combination (join with , + here) xi xj f(xi, xj) b b 6 b g 0 g b 0 g g 6 xj xk h(xi, xj, xk) b b b 12 b b g g b 0 b g g 6 g b b b g g g b 0 g g 6 6 g 0 0 g g 6 6 b September 2006 xj b b xi g(xj, xk) b xk 12 CP 06 = 0 6 41

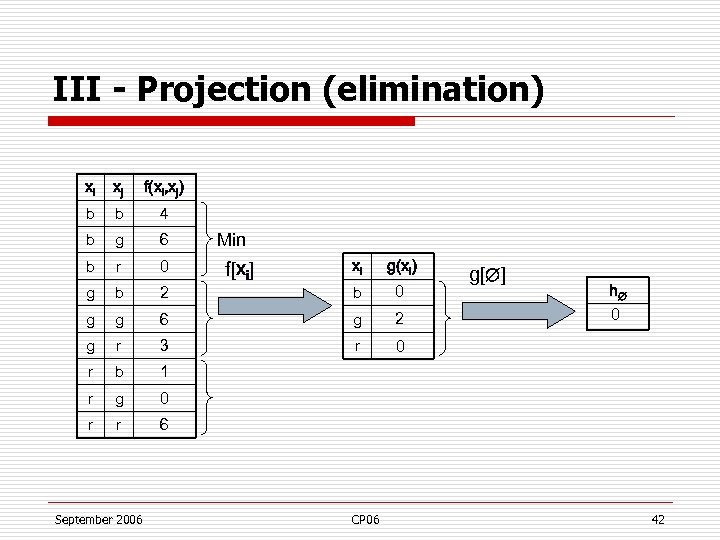III - Projection (elimination) xi xj f(xi, xj) b b 4 b g 6 b r 0 g b 2 g g g Min f[xi] xi g(xi) b 0 6 g 2 r 3 r 0 r b 1 r g 0 r r 6 September 2006 CP 06 g[ ] h 0 42

Properties o o Replacing two functions by their combination preserves the problem If f is the only function involving variable x, replacing f by f[-x] preserves the optimum September 2006 CP 06 43

Variable elimination 1. 2. 3. Select a variable Sum all functions that mention it Project the variable out • Complexity Time: (exp(deg+1)) Space: (exp(deg)) September 2006 CP 06 44

Variable elimination (aka bucket elimination) o o o Eliminate Variables one by one. When all variables have been eliminated, the problem is solved Optimal solutions of the original problem can be recomputed • Complexity: exponential in the induced width September 2006 CP 06 45

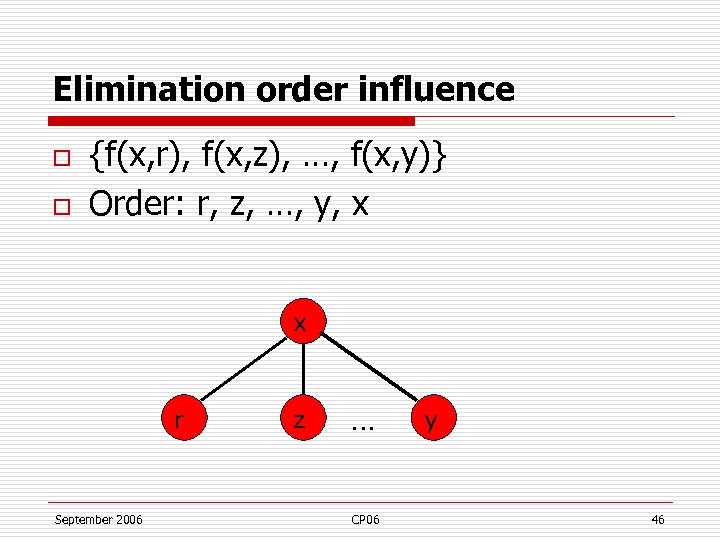Elimination order influence o o {f(x, r), f(x, z), …, f(x, y)} Order: r, z, …, y, x x r September 2006 z … CP 06 y 46

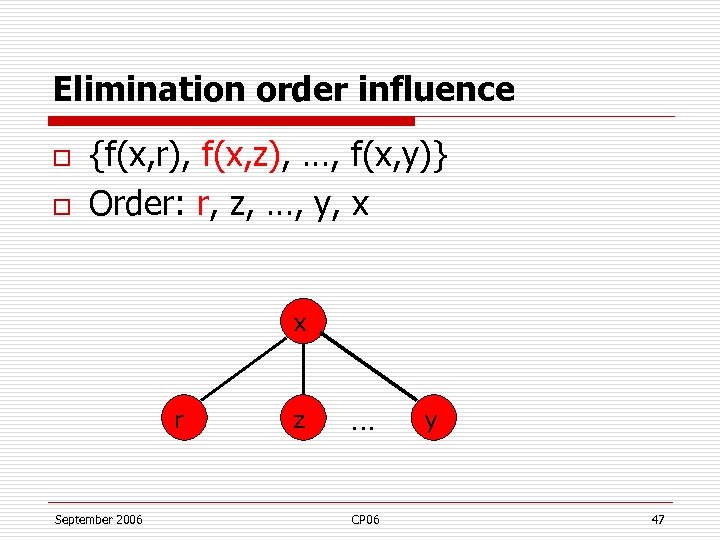Elimination order influence o o {f(x, r), f(x, z), …, f(x, y)} Order: r, z, …, y, x x r September 2006 z … CP 06 y 47

Elimination order influence o o {f(x), f(x, z), …, f(x, y)} Order: z, …, y, x x z September 2006 … CP 06 y 48

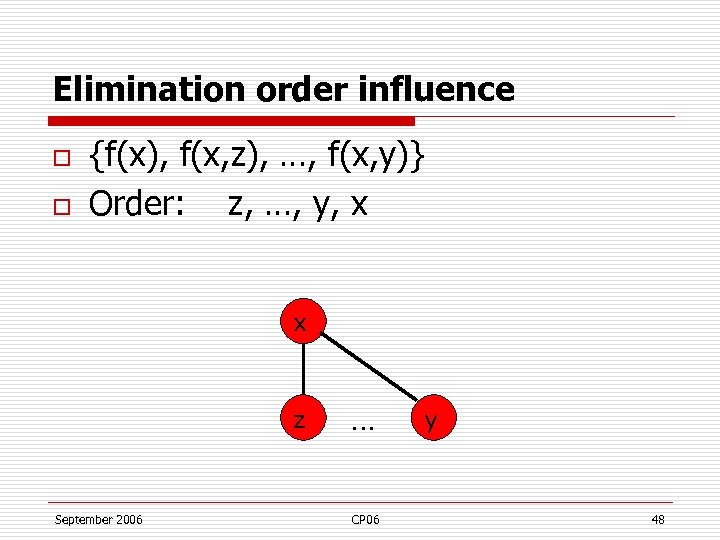
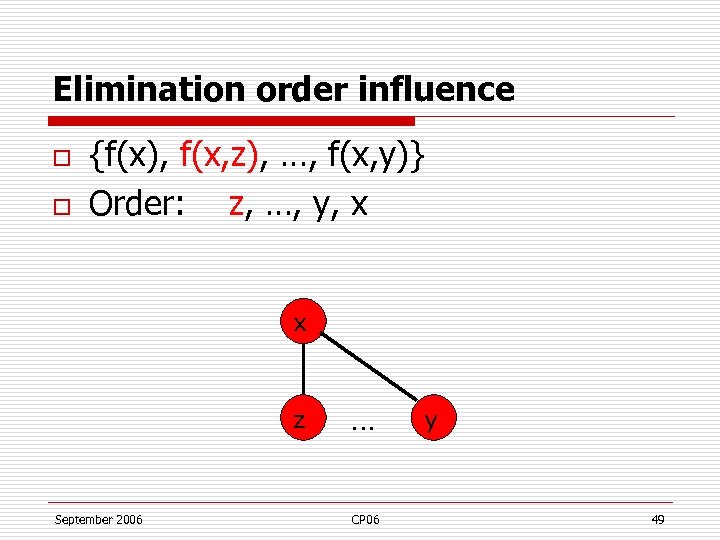Elimination order influence o o {f(x), f(x, z), …, f(x, y)} Order: z, …, y, x x z September 2006 … CP 06 y 49

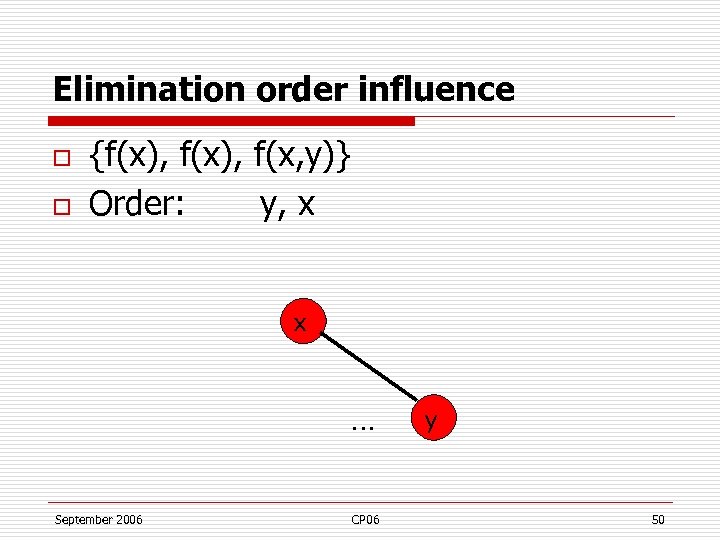Elimination order influence o o {f(x), f(x, y)} Order: y, x x … September 2006 CP 06 y 50

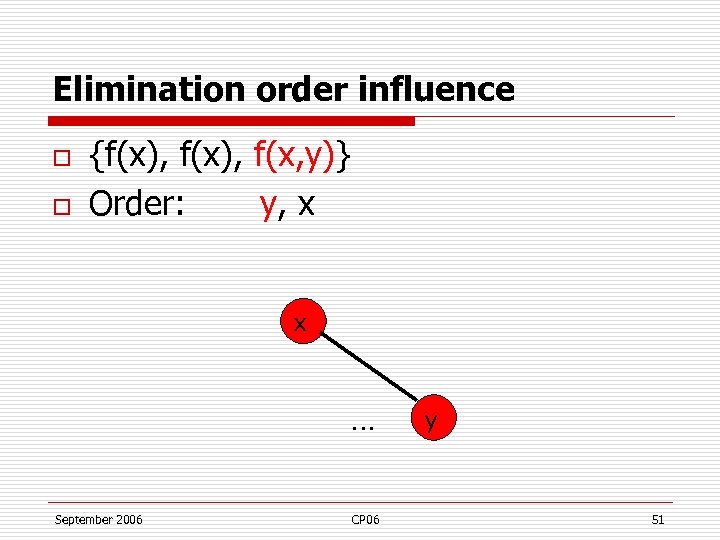Elimination order influence o o {f(x), f(x, y)} Order: y, x x … September 2006 CP 06 y 51

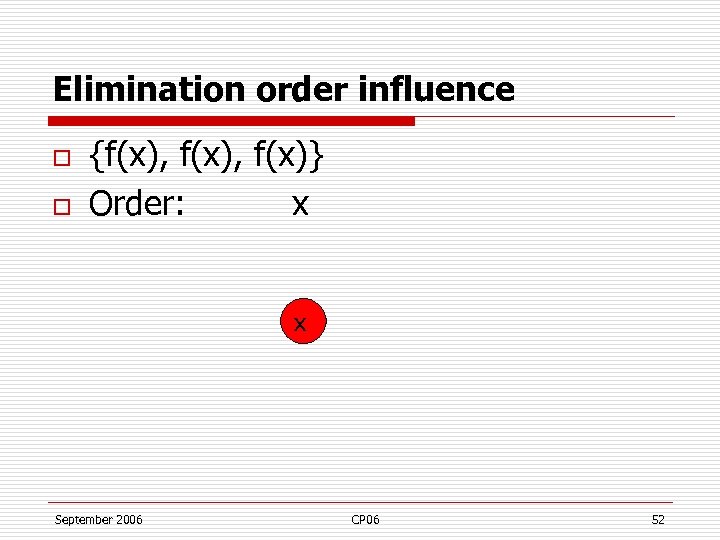Elimination order influence o o {f(x), f(x)} Order: x x September 2006 CP 06 52

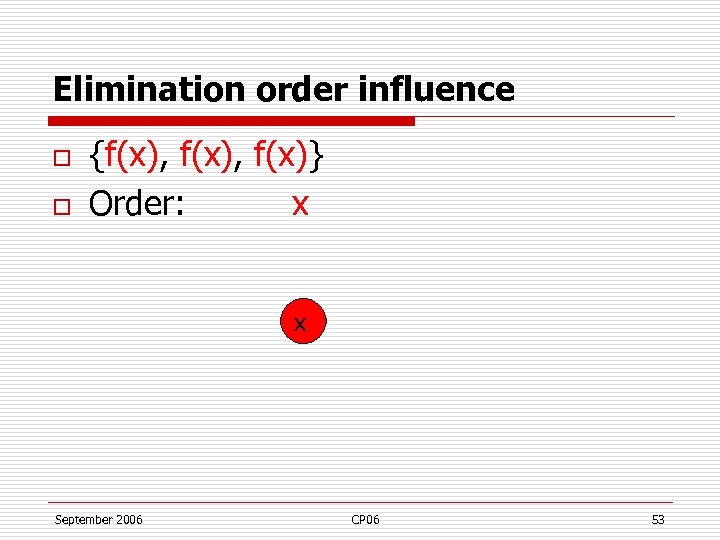Elimination order influence o o {f(x), f(x)} Order: x x September 2006 CP 06 53

Elimination order influence o o {f()} Order: September 2006 CP 06 54

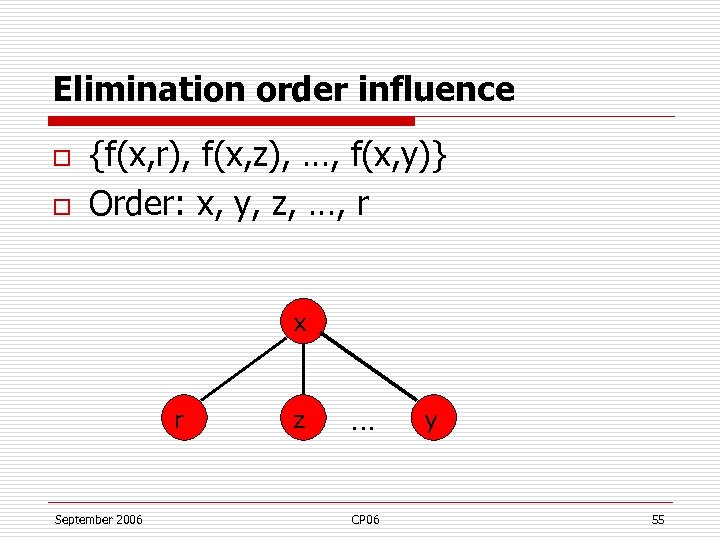Elimination order influence o o {f(x, r), f(x, z), …, f(x, y)} Order: x, y, z, …, r x r September 2006 z … CP 06 y 55

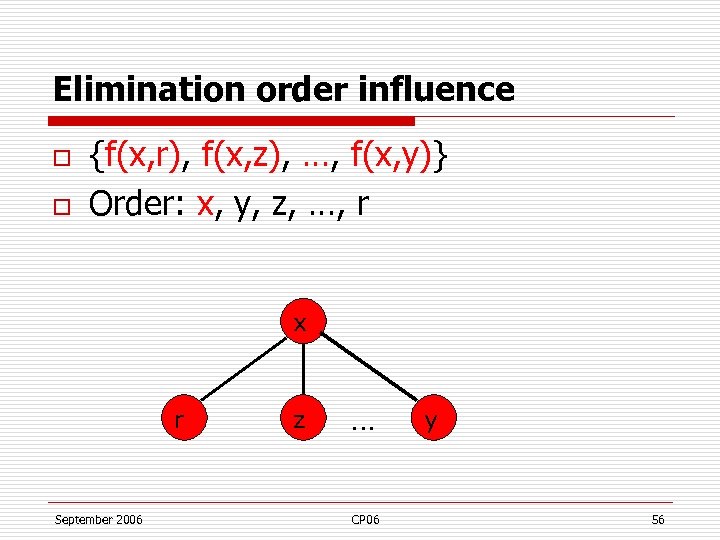Elimination order influence o o {f(x, r), f(x, z), …, f(x, y)} Order: x, y, z, …, r x r September 2006 z … CP 06 y 56

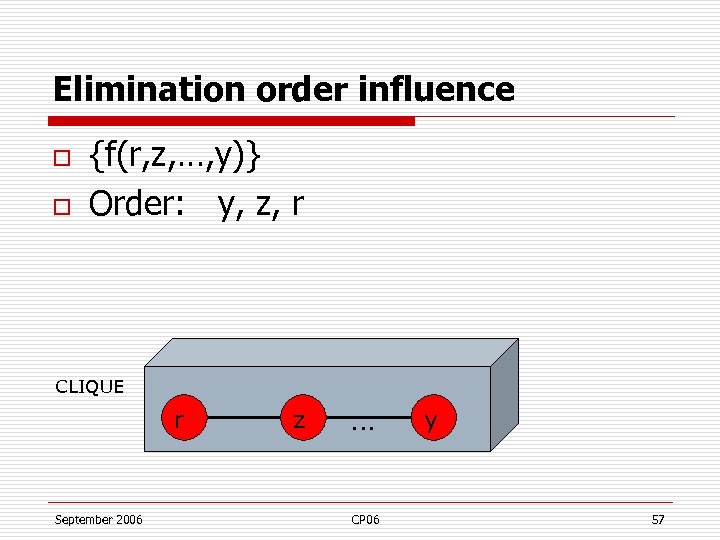Elimination order influence o o {f(r, z, …, y)} Order: y, z, r CLIQUE r September 2006 z … CP 06 y 57

Induced width o o For G=(V, E) and a given elimination (vertex) ordering, the largest degree encountered is the induced width of the ordered graph Minimizing induced width is NP-hard. September 2006 CP 06 58

Boosting search with variable elimination: BB-VE(k) o At each node n n n o Select an unassigned variable xi If degi ≤ k then eliminate xi Else branch on the values of xi Properties n n n BE-VE(-1) is BB BE-VE(w*) is VE BE-VE(1) is similar to cycle-cutset September 2006 CP 06 60

Boosting search with variable elimination o Ex: still-life (academic problem) n Instance: n=14 o n n n #var: 196 , #val: 2 Ilog Solver 5 days Variable Elimination 1 day BB-VE(18) 2 seconds September 2006 CP 06 61

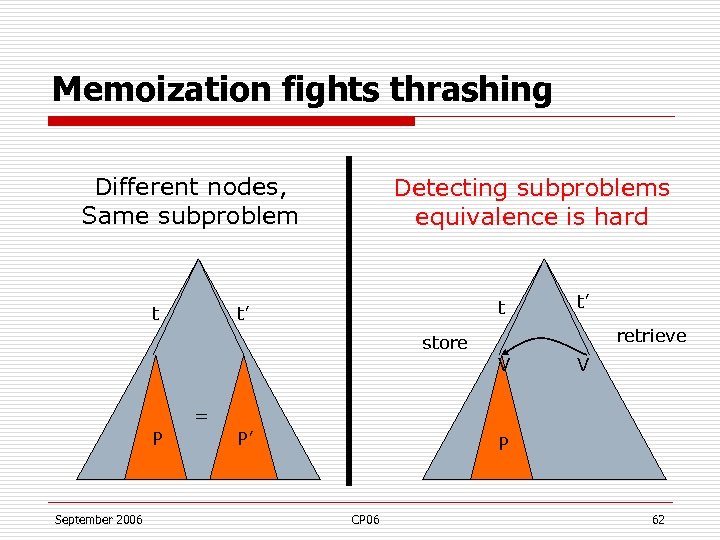Memoization fights thrashing Different nodes, Same subproblem t Detecting subproblems equivalence is hard t t’ store t’ retrieve V V = P September 2006 P’ P CP 06 62

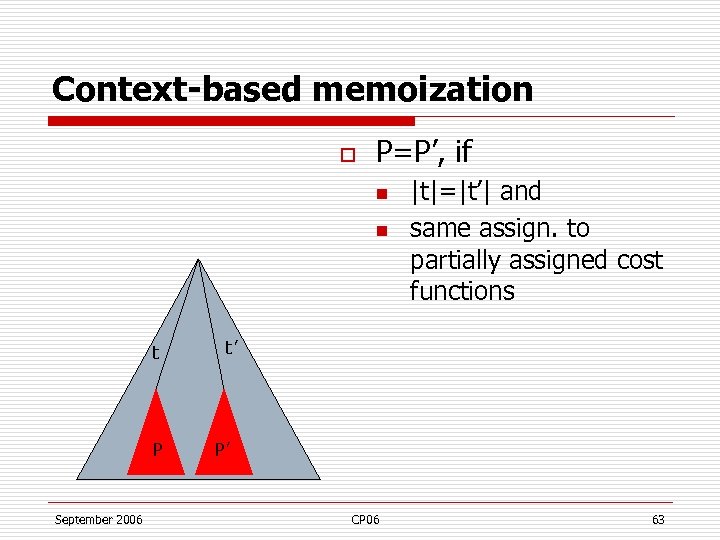Context-based memoization o P=P’, if n n t P September 2006 |t|=|t’| and same assign. to partially assigned cost functions t’ P’ CP 06 63

Memoization o Depth-first B&B with, n n o … is essentialy equivalent to VE n o o context-based memoization independent sub-problem detection Therefore space expensive Fresh approach: Easier to incorporate typical tricks such as propagation, symmetry breaking, … Algorithms: n n n Recursive Cond. (Darwiche 2001) BTD (Jégou and Terrioux 2003) AND/OR (Dechter et al, 2004) September 2006 CP 06 Adaptive memoization: time/space tradeoff 64

SAT inference o In SAT, inference = resolution x A ¬x B ------A B o o Effect: transforms explicit knowledge into implicit Complete inference: n n Resolve until quiescence Smart policy: variable by variable (Davis & Putnam, 60). Exponential on the induced width. September 2006 CP 06 65

Fair SAT Inference (A B, m), (x A, u⊖m), (x A, u), (¬x B, w) (¬x B, w⊖m), (x A ¬B, m), where: (¬x ¬A B, m) m=min{u, w} • Effect: moves knowledge September 2006 CP 06 66

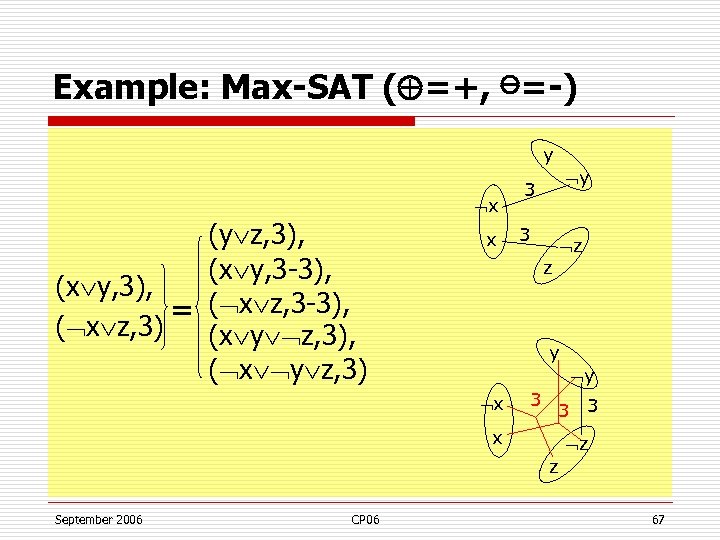Example: Max-SAT ( =+, ⊖=-) y x (y z, 3), (x y, 3 -3), (x y, 3), = ( x z, 3 -3), ( x z, 3) (x y z, 3), ( x y z, 3) x y 3 3 z z y y x 3 3 3 x z z September 2006 CP 06 67

Properties (Max-SAT) o o o In SAT, collapses to classical resolution Sound and complete Variable elimination: n n n o Select a variable x Resolve on x until quiescence Remove all clauses mentioning x Time and space complexity: exponential on the induced width September 2006 CP 06 68

Change September 2006 CP 06 69

Incomplete inference Local consistency Restricted resolution September 2006 CP 06

Incomplete inference o Tries to trade completeness for space/time n n o Produces only specific classes of cost functions Usually in polynomial time/space Local consistency: node, arc… n n n Equivalent problem Compositional: transparent use Provides a lb on consistency optimal cost September 2006 CP 06 71

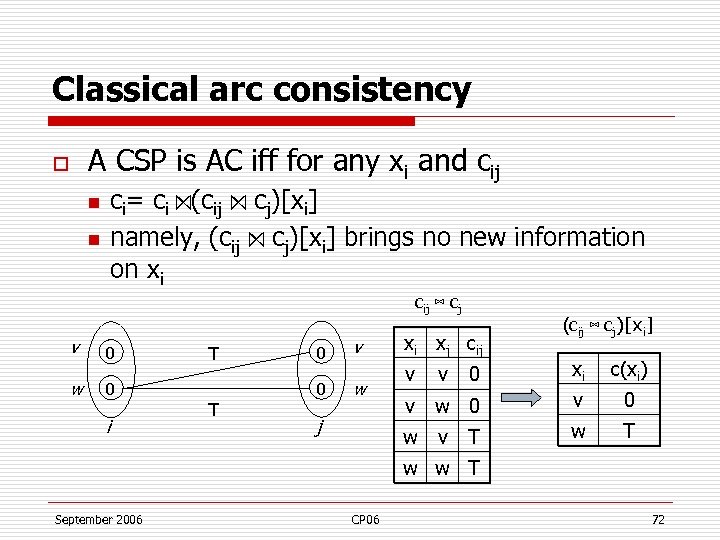Classical arc consistency A CSP is AC iff for any xi and cij o n n ci= ci ⋈(cij ⋈ cj)[xi] namely, (cij ⋈ cj)[xi] brings no new information on xi cij ⋈ cj v w 0 0 i T 0 v 0 T w xi xj cij (cij ⋈ cj)[xi] xi c(xi) v w 0 v 0 w v j 0 w T v v T w w T September 2006 CP 06 72

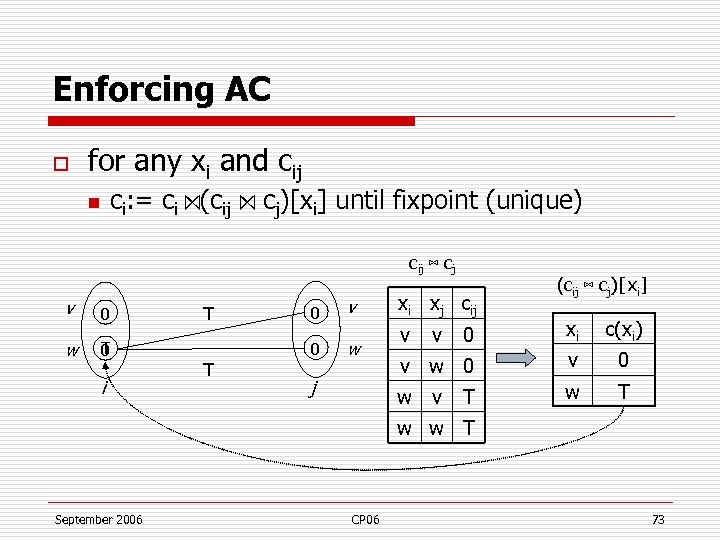Enforcing AC o for any xi and cij n ci: = ci ⋈(cij ⋈ cj)[xi] until fixpoint (unique) cij ⋈ cj v w 0 T 0 i T 0 v 0 T w xi xj cij (cij ⋈ cj)[xi] xi c(xi) v w 0 v 0 w v j 0 w T v v T w w T September 2006 CP 06 73

Arc consistency and soft constraints o for any xi and fij n f=(fij fj)[xi] brings no new information on xi fij fj (fij fj)[xi] w 0 1 0 i 1 v w j v v 0 Xi f(xi) v w 0 v 0 w v 0 0 2 fij 2 w 1 w w v xi xj 1 Always equivalent iff idempotent September 2006 CP 06 74

Idempotent soft CN o The previous operational extension works on any idempotent semiring CN n Chaotic iteration of local enforcing rules until fixpoint Terminates and yields an equivalent problem Extends to generalized k-consistency n Total order: idempotent ( = max) n n September 2006 CP 06 75

Non idempotent: weighted CN o for any xi and fij n f=(fij fj)[xi] brings no new information on xi fij fj v w 0 1 0 i 1 0 v 0 2 w xi xj fij fj [xi] xi f(xi) v w 0 v 0 w v j 0 w 1 v v 2 w w 1 EQUIVALENCE LOST September 2006 CP 06 76

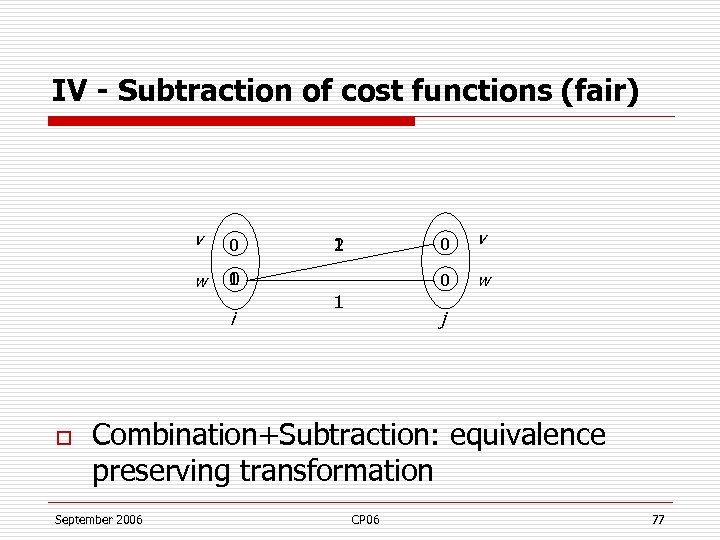IV - Subtraction of cost functions (fair) v 0 w 1 v 0 1 0 i o 0 1 2 w j Combination+Subtraction: equivalence preserving transformation September 2006 CP 06 77

(K, Y) equivalence preserving inference o For a set K of cost functions and a scope Y n n n Replace K by ( K) Add ( K)[Y] to the CN Subtract ( K)[Y] from ( K) (implied by K) o Yields an equivalent network All implicit information on Y in K is explicit o Repeat for a class of (K, Y) until fixpoint o September 2006 CP 06 78

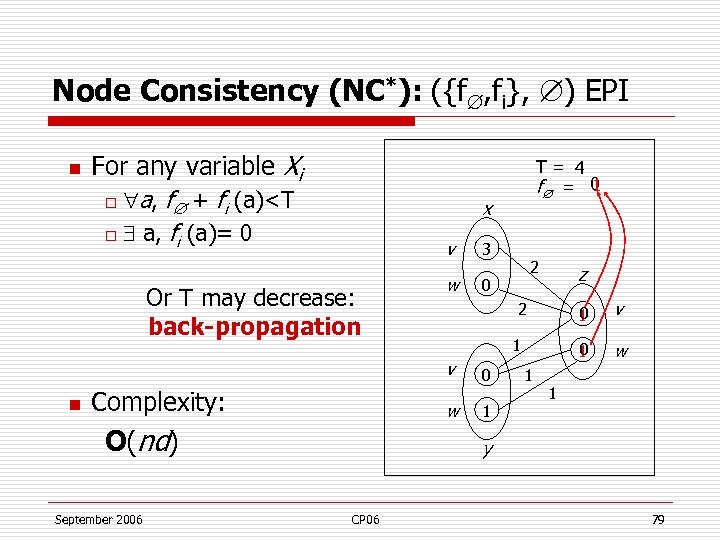Node Consistency (NC*): ({f , fi}, ) EPI n For any variable Xi a, f + fi (a)

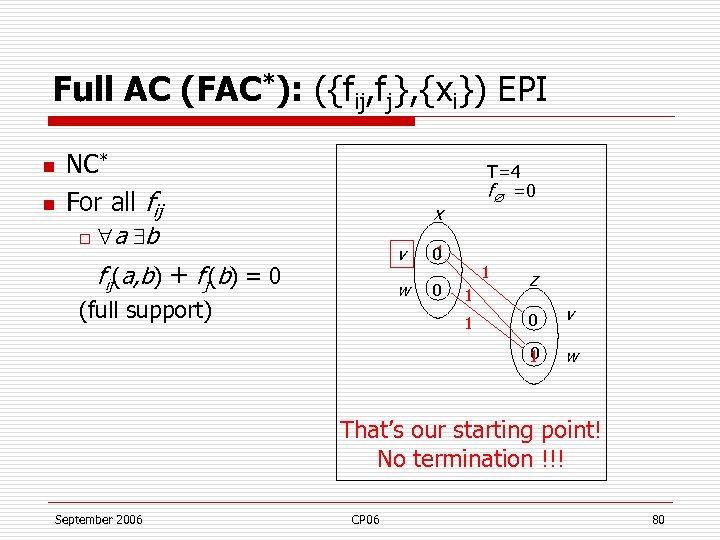Full AC (FAC*): ({fij, fj}, {xi}) EPI n n NC* For all fij o T=4 f =0 x a b v w fij(a, b) + fj(b) = 0 (full support) 1 0 0 1 1 z 0 v 0 1 1 w That’s our starting point! No termination !!! September 2006 CP 06 80

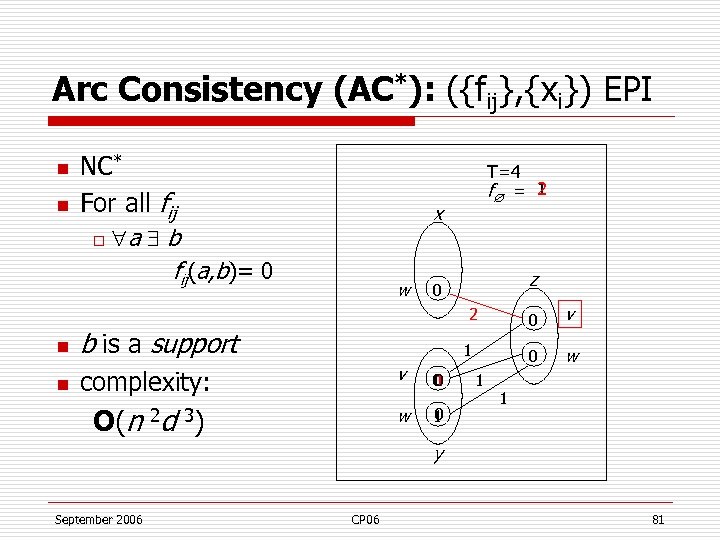Arc Consistency (AC*): ({fij}, {xi}) EPI n n NC* For all fij o T=4 2 f = 1 x a b fij(a, b)= 0 w z 0 0 n b is a support n complexity: v O(n 2 d 3) w 1 0 0 1 1 v 0 2 w 1 y September 2006 CP 06 81

Neighborhood Resolution (A, m), (x A, u⊖m), (x A, u), (¬x A, w) (¬x A, w⊖m), (x A ¬A, m), (¬x ¬A A, m) n if |A|=0, enforces node consistency n if |A|=1, enforces arc consistency September 2006 CP 06 82

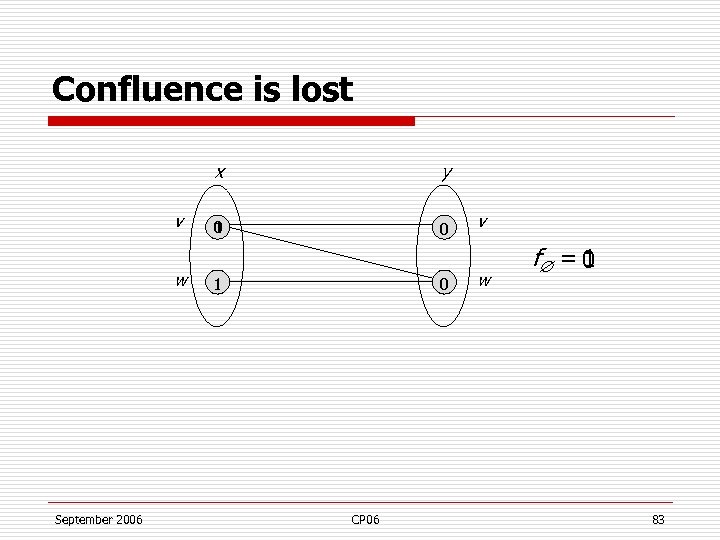Confluence is lost x v w September 2006 y 0 1 0 CP 06 v w f = 0 1 83

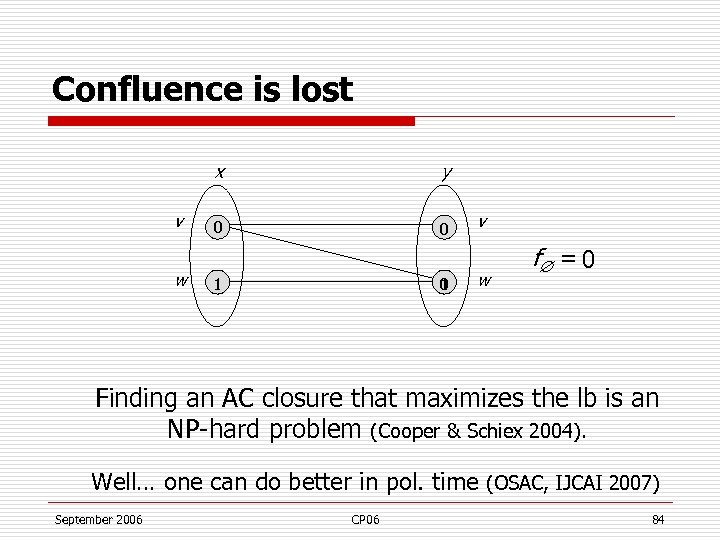Confluence is lost x v w y 0 0 1 v w f = 0 Finding an AC closure that maximizes the lb is an NP-hard problem (Cooper & Schiex 2004). Well… one can do better in pol. time (OSAC, IJCAI 2007) September 2006 CP 06 84

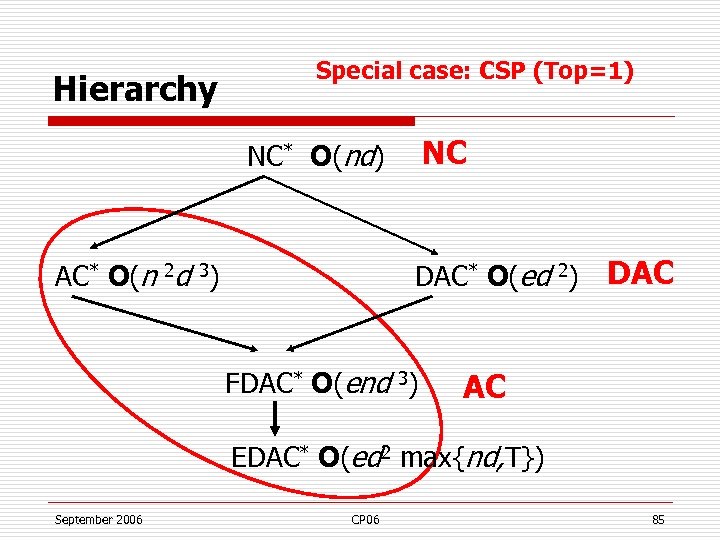Hierarchy Special case: CSP (Top=1) NC NC* O(nd) AC* O(n 2 d 3) DAC* O(ed 2) FDAC* O(end 3) DAC AC EDAC* O(ed 2 max{nd, T}) September 2006 CP 06 85

Boosting search with LC BT(X, D, C) if (X= ) then Top : =f else xj : = select. Var(X) forall a Dj do f. S C s. t. xj S f. S : = f. S [xj =a] if (LC) then BT(X-{xj}, D-{Dj}, C) September 2006 CP 06 86

MEDAC MFDAC MAC/MDAC MNC BT September 2006 CP 06 87

Boosting Systematic Search with Local consistency Frequency assignment problem o CELAR 6 -sub 4 (22 var, 44 val, 477 cost func): n n o MNC* 1 year MFDAC* 1 hour CELAR 6 (100 var, 44 val, 1322 cost func): n MEDAC+memoization 3 hours (toolbar-BTD) September 2006 CP 06 88

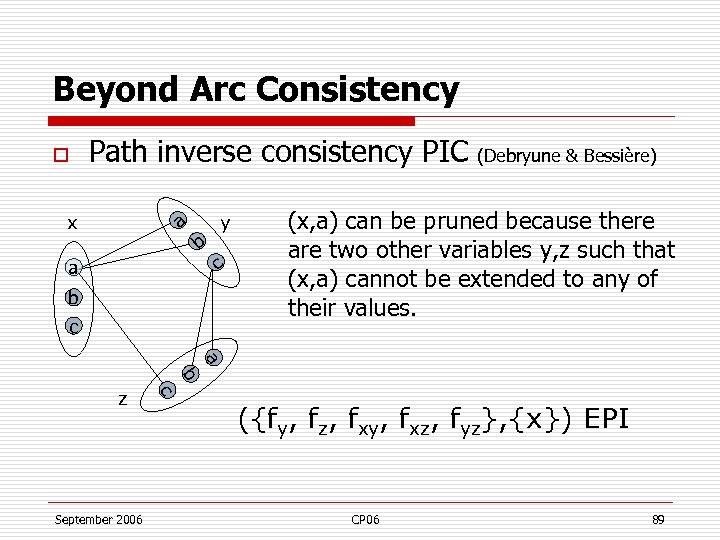Beyond Arc Consistency o Path inverse consistency PIC (Debryune & Bessière) a x b a y c b c (x, a) can be pruned because there are two other variables y, z such that (x, a) cannot be extended to any of their values. a b September 2006 c z ({fy, fz, fxy, fxz, fyz}, {x}) EPI CP 06 89

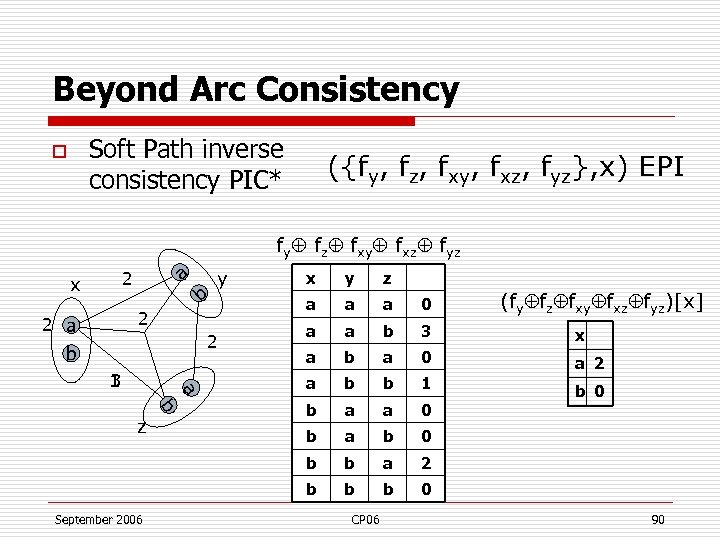Beyond Arc Consistency Soft Path inverse consistency PIC* o ({fy, fz, fxy, fxz, fyz}, x) EPI fy fz fxy fxz fyz a 2 y 2 2 a 2 b a 1 3 b z September 2006 y z a a a 0 2 a a b 3 5 x a b a 0 2 a b b 1 3 b a a 0 b a b 0 b a 2 b b x b b 0 CP 06 (fy fz fxy fxz fyz)[x] 90

Hyper-resolution (2 steps) (q A, m’), (h q A, m-m’), (l h A, u-m), ( h q A, u-m’), (l h A, u), ( l q A, v), = ( l q A, v-m), = (l h A, u-m), (l h q A, m), ( l q A, v-m), ( h q A, u) ( l q h A, m), (l h q A, m), ( h q A, u) ( l q h A, m) if |A|=0, equal to soft PIC Impressive empirical speed-ups September 2006 CP 06 91

Complexity & Polynomial classes Tree = induced width 1 Idempotent or not… September 2006 CP 06

Polynomial classes Idempotent VCSP: min-max CN o Can use -cuts for lifting CSP classes n n n Sufficient condition: the polynomial class is «conserved» by -cuts Simple TCSP are TCSP where all constraints use 1 interval: xi-xj∊[aij, bij] Fuzzy STCN: any slice of a cost function is an interval (semi-convex function) (Rossi et al. ) September 2006 CP 06 93

Hardness in the additive case (weighted/boolean) o Max. Sat is MAXSNP complete (no PTAS) n n n Weighted Max. SAT is FPNP-complete Max. SAT is FPNP[O(log(n))] complete: weights ! Max. SAT tractable langages fully characterized (Creignou 2001) o Max. CSP langage: feq(x, y) : (x = y) ? 0 : 1 is NP-hard. n Submodular cost function lang. is polynomial. (u ≤ x, v ≤ y September 2006 f(u, v)+f(x, y) ≤ f(u, y)+f(x, v)) CP 06 (Cohen et al. ) 94

Integration of soft constraints into classical constraint programming Soft as hard Soft local consistency as a global constraint September 2006 CP 06

Soft constraints as hard constraints o o one extra variable xs per cost function f. S all with domain E f. S ➙ c. S∪{x. S} allowing (t, f. S(t)) for all t∊ℓ(S) one variable x. C = xs (global constraint) September 2006 CP 06 96

Soft as Hard (Sa. H) o Criterion represented as a variable Multiple criteria = multiple variables Constraints on/between criteria o Weaknesses: o o n n n Extra variables (domains), increased arities Sa. H constraints give weak GAC propagation Problem structure changed/hidden September 2006 CP 06 97

≥ Soft AC « stronger than » Sas. H GAC o o Ø o o Take a WCSP Enforce Soft AC on it Each cost function contains at least one tuple with a 0 cost (definition) Soft as Hard: the cost variable x. C will have a lb of 0 The lower bound cannot improve by GAC September 2006 CP 06 98

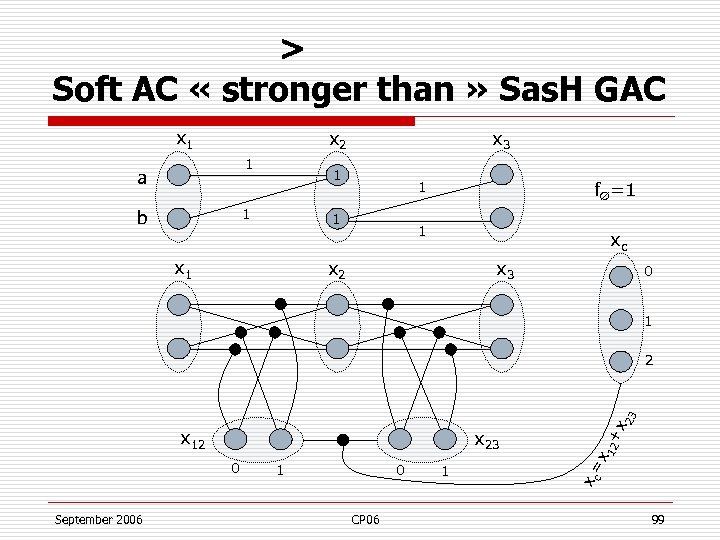> Soft AC « stronger than » Sas. H GAC x 1 x 2 1 a 1 1 b x 3 1 1 1 x 1 f∅=1 xc x 2 x 3 0 1 September 2006 1 0 CP 06 1 12 + x 0 c x 23 x= x 12 x 23 2 99

Soft local Consistency as a Global constraint ( =+) o Global constraint: Soft(X, F, C) n n n o o o X F C variables cost functions interval cost variable (ub = T) Semantics: X U{C} satisfy Soft(X, F, C) iff f(X)=C Enforcing GAC on Soft is NP-hard Soft consistency: filtering algorithm (lb≥f ) September 2006 CP 06 100

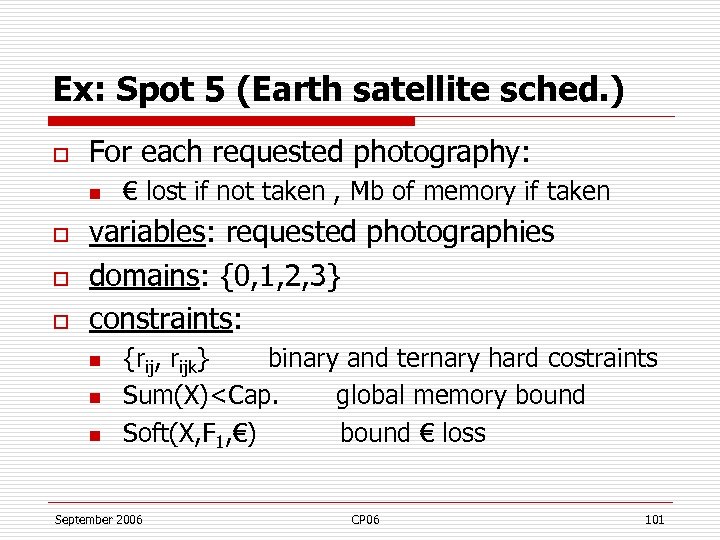Ex: Spot 5 (Earth satellite sched. ) o For each requested photography: n o o o € lost if not taken , Mb of memory if taken variables: requested photographies domains: {0, 1, 2, 3} constraints: n n n {rij, rijk} binary and ternary hard costraints Sum(X)

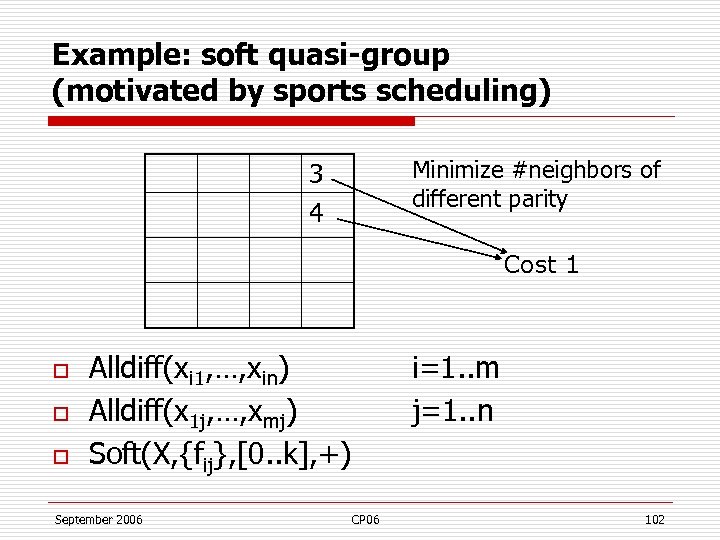Example: soft quasi-group (motivated by sports scheduling) Minimize #neighbors of different parity 3 4 Cost 1 o o o Alldiff(xi 1, …, xin) Alldiff(x 1 j, …, xmj) Soft(X, {fij}, [0. . k], +) September 2006 i=1. . m j=1. . n CP 06 102

Global soft constraints September 2006 CP 06

Global soft constraints o Idea: define a library of useful but nonstandard objective functions along with efficient filtering algorithms n All. Diff (2 semantics: Petit et al 2001, van Hoeve 2004) Soft global cardinality (van Hoeve et al. 2004) Soft regular (van Hoeve et al. 2004) n … all enforce reified GAC n n September 2006 CP 06 104

Conclusion o o A large subset of classic CN body of knowledge has been extended to soft CN, efficient solving tools exist. Much remains to be done: n n n Extension: to other problems than optimization (counting, quantification…) Techniques: symmetries, learning, knowledge compilation… Algorithmic: still better lb, other local consistencies or dominance. Global (Soft. As. Soft). Exploiting problem structure. Implementation: better integration with classic CN solver (Choco, Solver, Minion…) Applications: problem modelling, solving, heuristic guidance, partial solving. September 2006 CP 06 105

30’’ of publicity September 2006 CP 06

Open source libraries Toolbar and Toulbar 2 o Accessible from the Soft wiki site: carlit. toulouse. inra. fr/cgi-bin/awki. cgi/Soft. CSP o Alg: BE-VE, MNC, MAC, MDAC, MFDAC, MEDAC, MPIC, BTD ILOG connection, large domains/problems… Read Max. CSP/SAT (weighted or not) and ERGO format Thousands of benchmarks in standardized format Pointers to other solvers (Max. SAT/CSP) Pwd: bia 31 o Forge mulcyber. toulouse. inra. fr/projects/toolbar o o (toulbar 2) September 2006 CP 06 107

Thank you for your attention This is it ! o o o S. Bistarelli, U. Montanari and F. Rossi, Semiring-based Constraint Satisfaction and Optimization, Journal of ACM, vol. 44, n. 2, pp. 201 -236, March 1997. S. Bistarelli, H. Fargier, U. Montanari, F. Rossi, T. Schiex, G. Verfaillie. Semiring. Based CSPs and Valued CSPs: Frameworks, Properties, and Comparison. CONSTRAINTS, Vol. 4, N. 3, September 1999. S. Bistarelli, R. Gennari, F. Rossi. Constraint Propagation for Soft Constraint Satisfaction Problems: Generalization and Termination Conditions , in Proc. CP 2000 o o o o C. Blum and A. Roli. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Computing Surveys, 35(3): 268 -308, 2003. T. Schiex, Arc consistency for soft constraints, in Proc. CP’ 2000. M. Cooper, T. Schiex. Arc consistency for soft constraints, Artificial Intelligence, Volume 154 (1 -2), 199 -227 2004. M. Cooper. Reduction Operations in fuzzy or valued constraint satisfaction problems. Fuzzy Sets and Systems 134 (3) 2003. A. Darwiche. Recursive Conditioning. Artificial Intelligence. Vol 125, No 1 -2, pages 5 -41. R. Dechter. Bucket Elimination: A unifying framework for Reasoning. Artificial Intelligence, October, 1999. R. Dechter, Mini-Buckets: A General Scheme For Generating Approximations In Automated Reasoning In Proc. Of IJCAI 97 September 2006 CP 06 108

References o o o o o S. de Givry, F. Heras, J. Larrosa & M. Zytnicki. Existential arc consistency: getting closer to full arc consistency in weighted CSPs. In IJCAI 2005. W. -J. van Hoeve, G. Pesant and L. -M. Rousseau. On Global Warming: Flow-Based Soft Global Constraints. Journal of Heuristics 12(4 -5), pp. 347 -373, 2006. P. Jegou & C. Terrioux. Hybrid backtracking bounded by tree-decomposition of constraint networks. Artif. Intell. 146(1): 43 -75 (2003) J. Larrosa & T. Schiex. Solving Weighted CSP by Maintaining Arc Consistency. Artificial Intelligence. 159 (1 -2): 1 -26, 2004. J. Larrosa and T. Schiex. In the quest of the best form of local consistency for Weighted CSP, Proc. of IJCAI'03 J. Larrosa, P. Meseguer, T. Schiex Maintaining Reversible DAC for MAX-CSP. Artificial Intelligence. 107(1), pp. 149 -163. R. Marinescu and R. Dechter. AND/OR Branch-and-Bound for Graphical Models. In proceedings of IJCAI'2005. J. C. Regin, T. Petit, C. Bessiere and J. F. Puget. An original constraint based approach for solving over constrained problems. In Proc. CP'2000. T. Schiex, H. Fargier et G. Verfaillie. Valued Constraint Satisfaction Problems: hard and easy problems In Proc. of IJCAI 95. G. Verfaillie, M. Lemaitre et T. Schiex. Russian Doll Search Proc. of AAAI'96. September 2006 CP 06 109

References o o o o M. Bonet, J. Levy and F. Manya. A complete calculus for max-sat. In SAT 2006. M. Davis & H. Putnam. A computation procedure for quantification theory. In JACM 3 (7) 1960. I. Rish and R. Dechter. Resolution versus Search: Two Strategies for SAT. In Journal of Automated Reasoning, 24 (1 -2), 2000. F. Heras & J. Larrosa. New Inference Rules for Efficient Max-SAT Solving. In AAAI 2006. J. Larrosa, F. Heras. Resolution in Max-SAT and its relation to local consistency in weighted CSPs. In IJCAI 2005. C. M. Li, F. Manya and J. Planes. Improved branch and bound algorithms for maxsat. In AAAI 2006. H. Shen and H. Zhang. Study of lower bounds for max-2 -sat. In proc. of AAAI 2004. Z. Xing and W. Zhang. Max. Solver: An efficient exact algorithm for (weighted) maximum satisfiability. Artificial Intelligence 164 (1 -2) 2005. September 2006 CP 06 110

Softas. Hard GAC vs. EDAC 25 variables, 2 values binary Max. CSP o Toolbar MEDAC n n n o opt=34 220 nodes cpu-time = 0’’ GAC on Softas. Hard, ILOG Solver 6. 0, solve n n opt = 34 339136 choice points cpu-time: 29. 1’’ Uses table constraints September 2006 CP 06 111

Other hints on Softas. Hard GAC o Max. SAT as Pseudo Boolean Soft. As. Hard n n For each clause: c = (x … z, pc) c. SAH = (x … z rc) Extra cardinality constraint: Σ pc. rc ≤ k n Used by SAT 4 JMax. Sat (Max. SAT competition). September 2006 CP 06 112

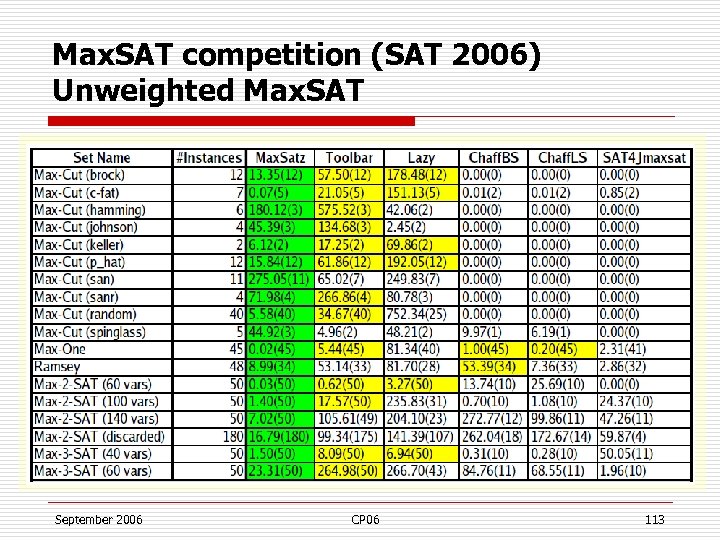Max. SAT competition (SAT 2006) Unweighted Max. SAT September 2006 CP 06 113

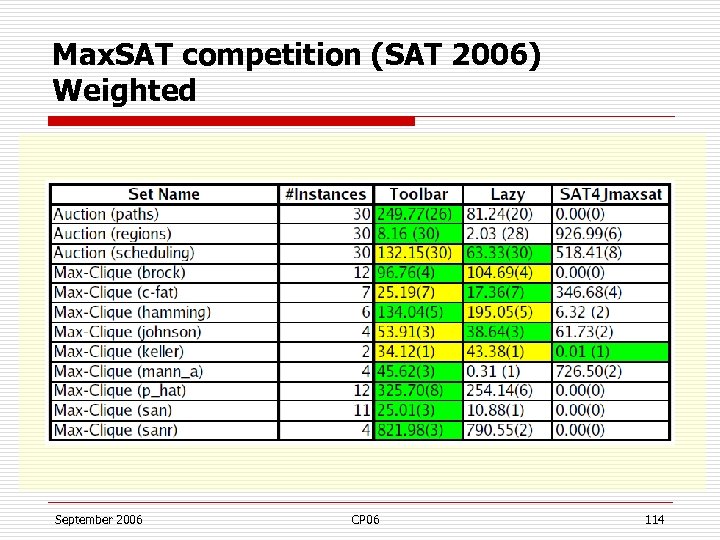Max. SAT competition (SAT 2006) Weighted September 2006 CP 06 114