Thermodynamics Lecture Series Entropy Quantifying Energy Degradation

Thermodynamics Lecture Series Entropy – Quantifying Energy Degradation Applied Sciences Education Research Group (ASERG) Faculty of Applied Sciences Universiti Teknologi MARA email: drjjlanita@hotmail. com http: //www 5. uitm. edu. my/faculties/fsg/drjj 1. html

Quotes • “The principal goal of education is to create men and women who are capable of doing new things, not simply repeating what other generations have done” Jean Piaget • “What we have to learn to do, we learn by doing” Einstein

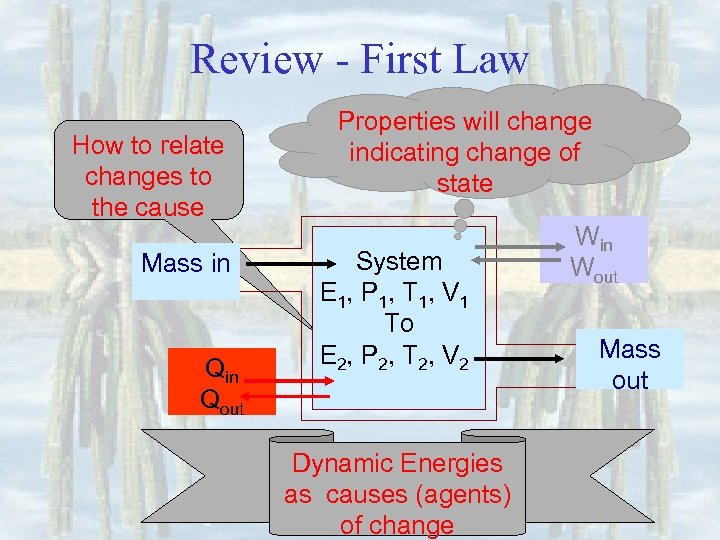Review - First Law How to relate changes to the cause Mass in Qout Properties will change indicating change of state System E 1, P 1, T 1, V 1 To E 2, P 2, T 2, V 2 Dynamic Energies as causes (agents) of change Win Wout Mass out

Review - First Law Energy Change of Entering - Leaving = system’s a system energy Energy Balance Ein – Eout = Esys, k. J or ein – eout = esys, k. J/kg or

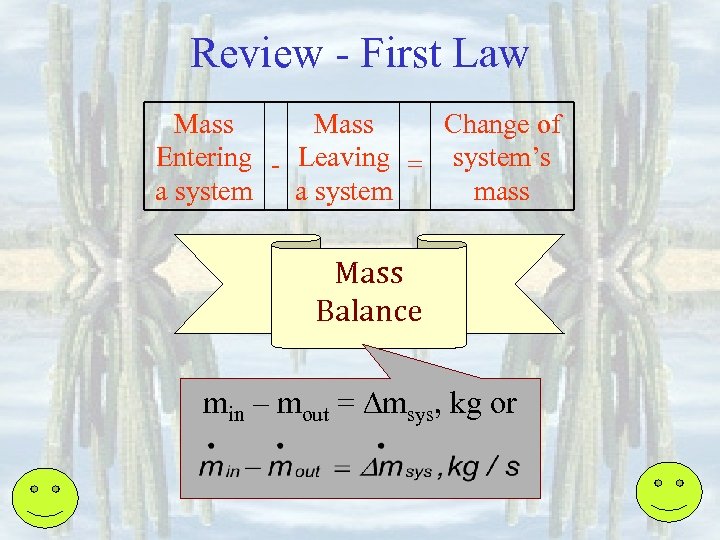Review - First Law Mass Change of Entering - Leaving = system’s a system mass Mass Balance min – mout = msys, kg or

Review - First Law Energy Balance – Control Volume Steady-Flow Steady-flow is a flow where all properties within boundary of the system remains constant with time Esys= 0, k. J; esys= 0 , k. J/kg, Vsys= 0, m 3; msys= 0 or min = mout , kg

Review - First Law Mass & Energy Balance –Steady-Flow: Single Stream Mass balance Energy balance qin – qout+ in – out = qout – qin, k. J/kg

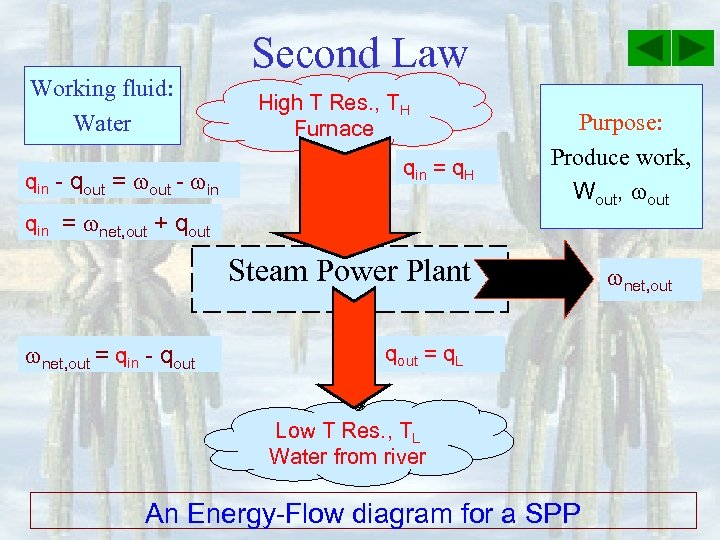Working fluid: Water qin - qout = out - in Second Law High T Res. , TH Furnace qin = q. H qin = net, out + qout Purpose: Produce work, Wout, out Steam Power Plant net, out = qin - qout = q. L Low T Res. , TL Water from river An Energy-Flow diagram for a SPP net, out

Second Law Thermal Efficiency for steam power plants

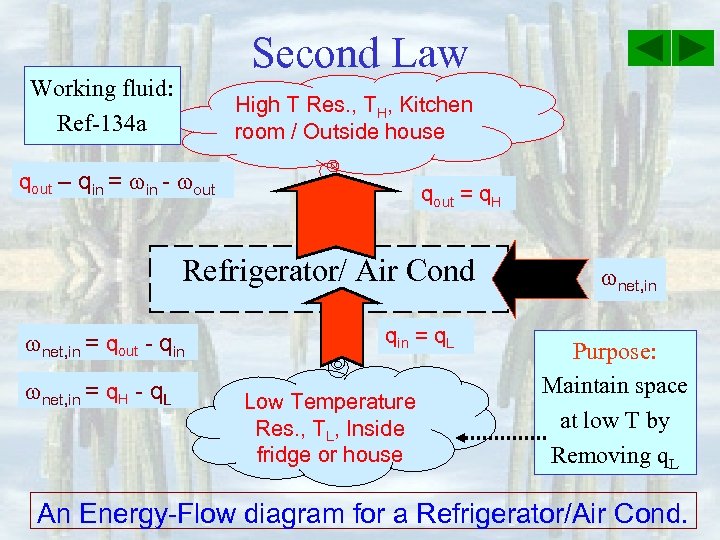Second Law Working fluid: Ref-134 a High T Res. , TH, Kitchen room / Outside house qout – qin = in - out qout = q. H Refrigerator/ Air Cond net, in = qout - qin net, in = q. H - q. L qin = q. L Low Temperature Res. , TL, Inside fridge or house net, in Purpose: Maintain space at low T by Removing q. L An Energy-Flow diagram for a Refrigerator/Air Cond.

Second Law Coefficient of Performance for a Refrigerator

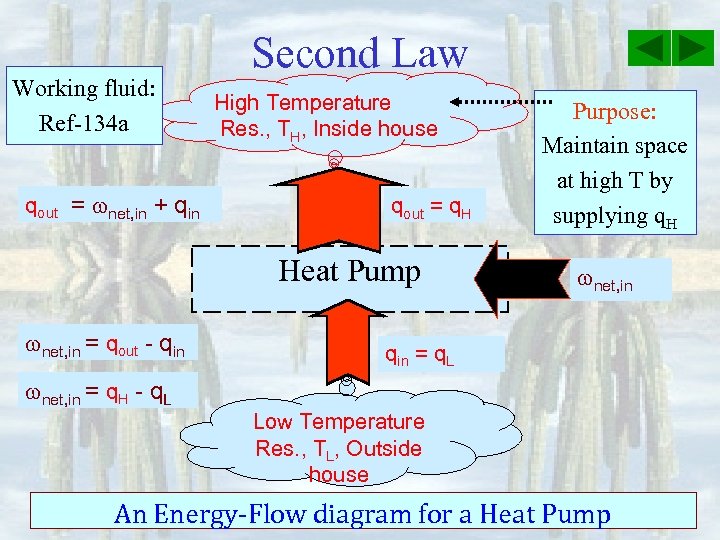Working fluid: Ref-134 a qout = net, in + qin Second Law High Temperature Res. , TH, Inside house qout = q. H Heat Pump net, in = qout - qin Purpose: Maintain space at high T by supplying q. H net, in qin = q. L net, in = q. H - q. L Low Temperature Res. , TL, Outside house An Energy-Flow diagram for a Heat Pump

Second Law Coefficient of Performance for a Heat Pump

Second Law – Energy Degrade What is the maximum performance of real engines if it can never achieve 100%? ? Factors of irreversibilities • less heat can be converted to work – Friction between 2 moving surfaces – Processes happen too fast – Non-isothermal heat transfer

Second Law – Dream Engine Carnot Cycle • Isothermal expansion v. Slow adding of Q resulting in work done by system (system expand) v. Qin – Wout = U = 0. So, Qin = Wout. Pressure drops. • Adiabatic expansion v 0 – Wout = U. Final U smaller than initial U. v. T & P drops.

Second Law – Dream Engine Carnot Cycle • Isothermal compression v. Work done on the system v. Slow rejection of Q v- Qout + Win = U = 0. So, Qout = Win. v. Pressure increases. • Adiabatic compression v 0 + Win = U. Final U higher than initial U. v. T & P increases.

Second Law – Dream Engine Carnot Cycle P, k. Pa P - diagram for a Carnot (ideal) power plant 1 qin 2 4 3 qout , m 3/kg

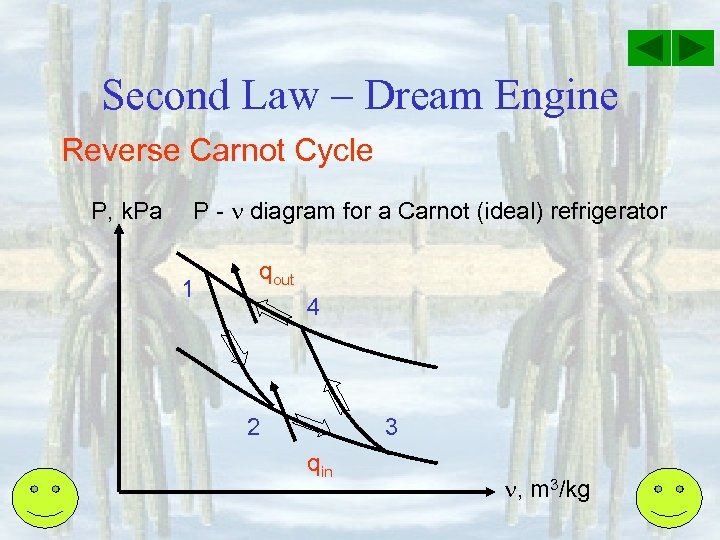Second Law – Dream Engine Reverse Carnot Cycle P, k. Pa P - diagram for a Carnot (ideal) refrigerator 1 qout 4 2 3 qin , m 3/kg

Second Law – Dream Engine Carnot Principles • For heat engines in contact with the same hot and cold reservoir v. All reversible engines have the same performance. v. Real engines will have lower performance than the ideal engines.

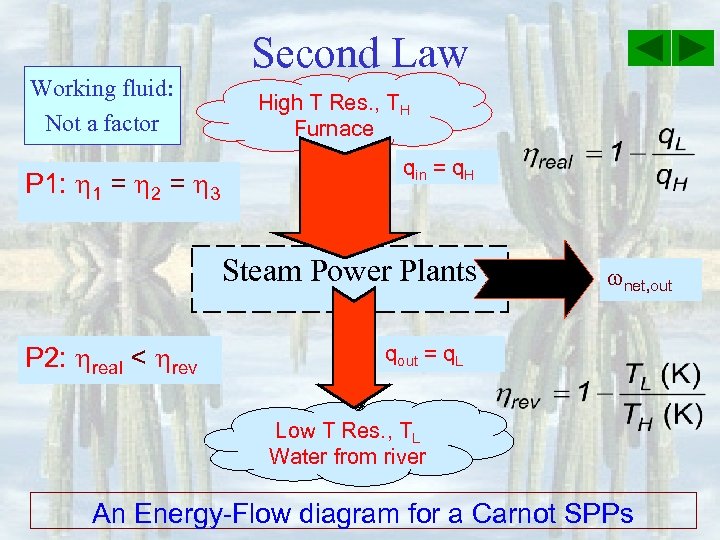Working fluid: Not a factor P 1: 1 = 2 = 3 Second Law High T Res. , TH Furnace qin = q. H Steam Power Plants P 2: real < rev net, out qout = q. L Low T Res. , TL Water from river An Energy-Flow diagram for a Carnot SPPs

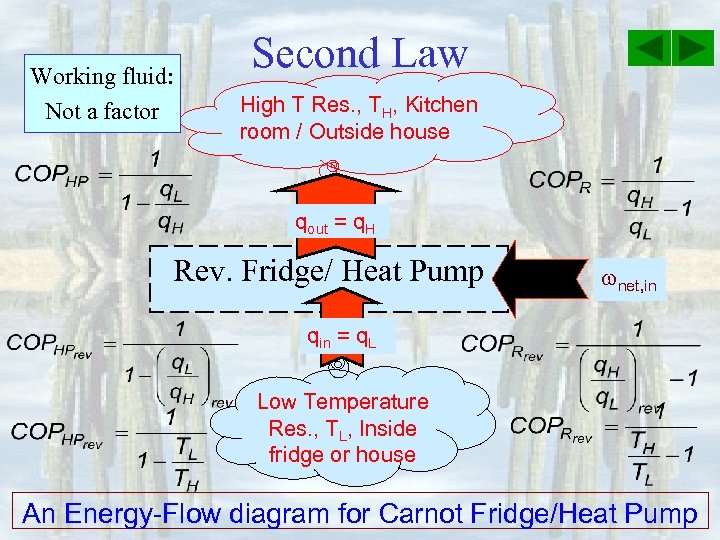Working fluid: Not a factor Second Law High T Res. , TH, Kitchen room / Outside house qout = q. H Rev. Fridge/ Heat Pump net, in qin = q. L Low Temperature Res. , TL, Inside fridge or house An Energy-Flow diagram for Carnot Fridge/Heat Pump

Second Law – Will a Process Happen Carnot Principles • For heat engines in contact with the same hot and cold reservoir v. P 1: 1 = 2 = 3 (Equality) v. P 2: real < rev (Inequality) Processes satisfying Carnot Principles obeys the Second Law of Thermodynamics

Second Law – Will a Process Happen Clausius Inequality : • Sum of Q/T in a cyclic process must be zero for reversible processes and negative for real processes reversible impossible real

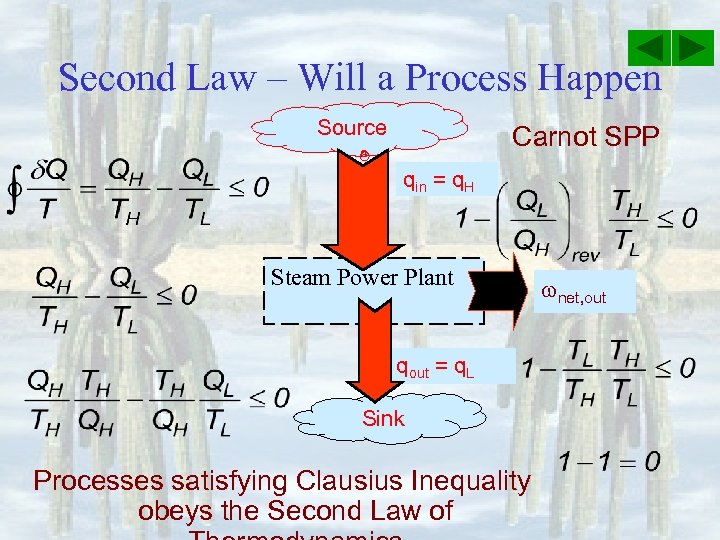Second Law – Will a Process Happen Source Carnot SPP qin = q. H Steam Power Plant qout = q. L Sink Processes satisfying Clausius Inequality obeys the Second Law of net, out

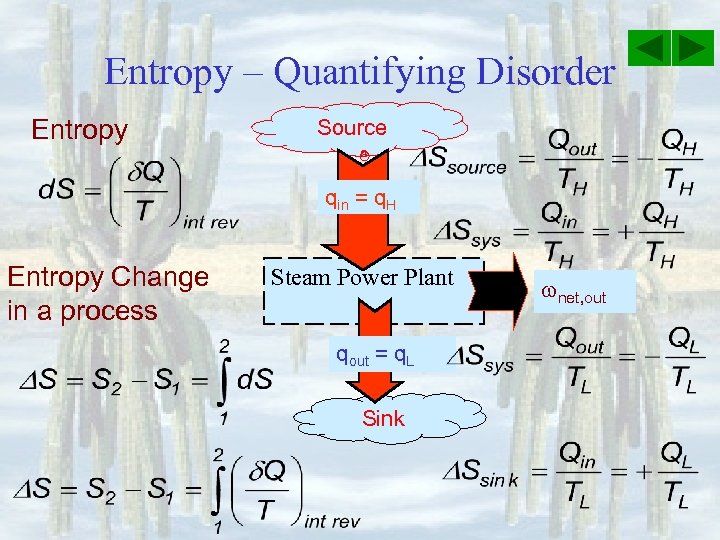Entropy – Quantifying Disorder Entropy Source qin = q. H Entropy Change in a process Steam Power Plant qout = q. L Sink net, out

Entropy – Quantifying Disorder • Entropy üQuantitative measure of disorder or chaos üIs a system’s property, just like the others üDoes not depend on process path üHas values at every state

Entropy – Quantifying Disorder Entropy ü Quantifies lost of energy quality ü Can be transferred by heat and mass or ü generated due to irreversibilty factors: Ø Frictional forces between moving surfaces. Ø Fast expansion & compression. Ø Heat transfer at finite temperature difference.

Entropy – Quantifying Disorder Increase of Entropy Principle The entropy of an isolated (closed and adiabatic) system undergoing any process, will always increase. Surrounding For pure substance: System

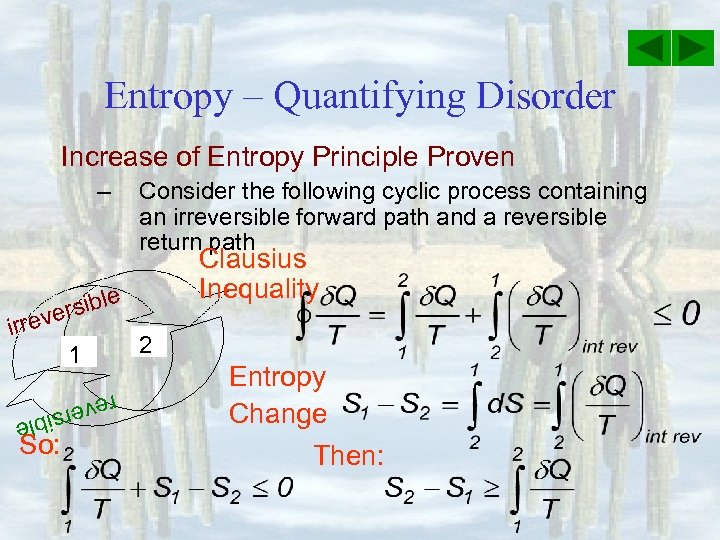Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Clausius Inequality e rsibl e irrev 1 reve e rsibl So: 2 Entropy Change Then:

Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Then entropy change for the closed system: e rsibl e irrev 1 2 reve e rsibl

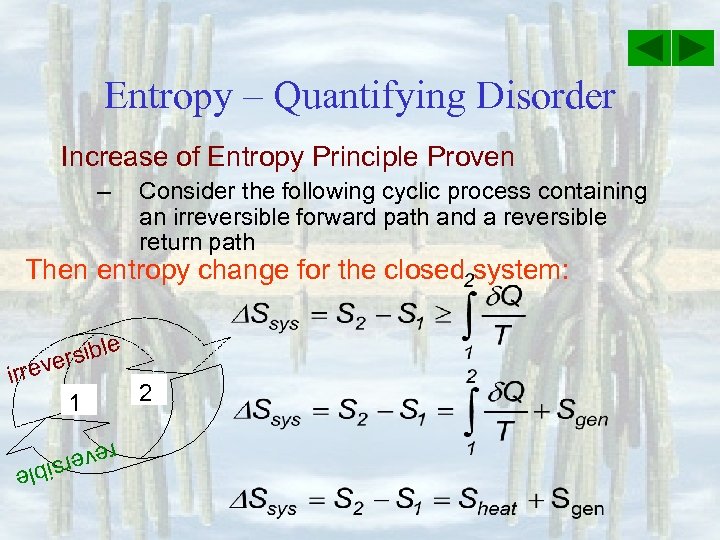Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Then entropy change for the closed system: e rsibl e irrev 1 2 reve e rsibl

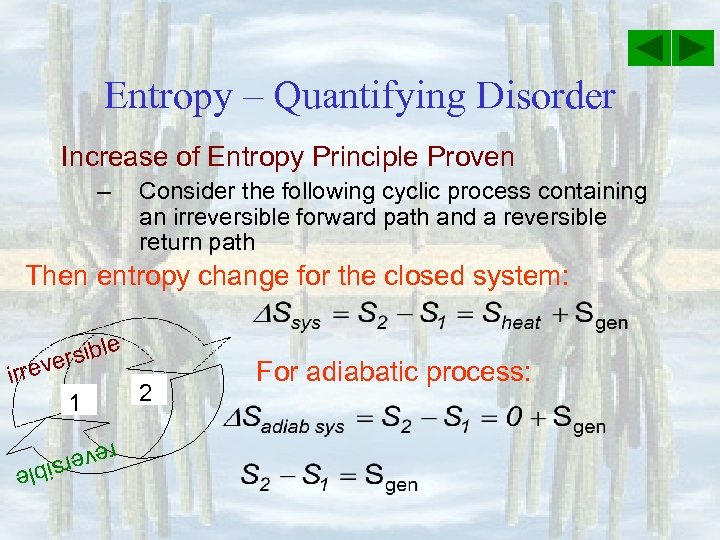Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Then entropy change for the closed system: e rsibl e irrev 1 2 For adiabatic process: reve e rsibl

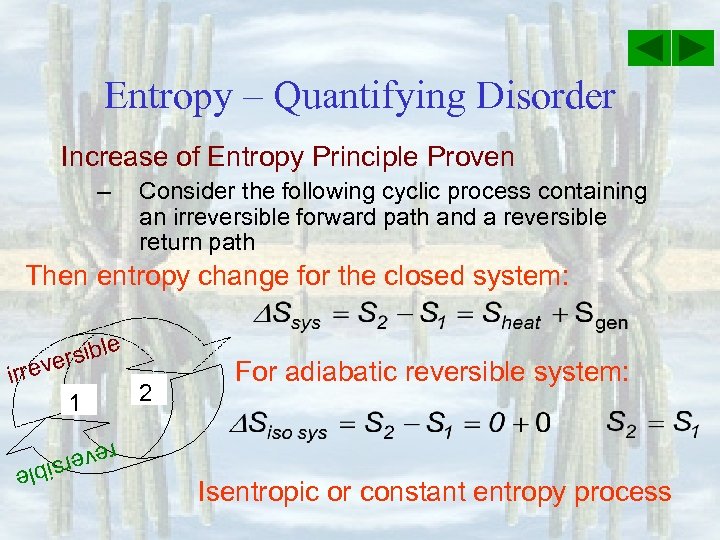Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Then entropy change for the closed system: e rsibl e irrev 1 2 For adiabatic reversible system: reve Isentropic or constant entropy process e rsibl

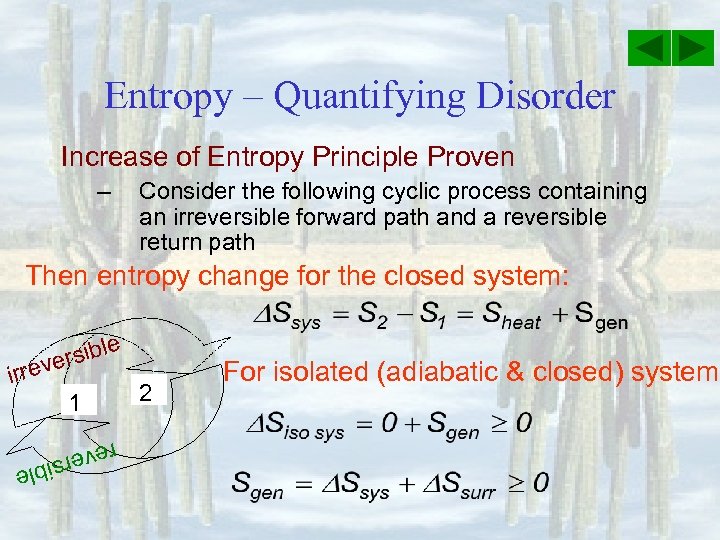Entropy – Quantifying Disorder Increase of Entropy Principle Proven – Consider the following cyclic process containing an irreversible forward path and a reversible return path Then entropy change for the closed system: e rsibl e irrev 1 2 For isolated (adiabatic & closed) system: reve e rsibl

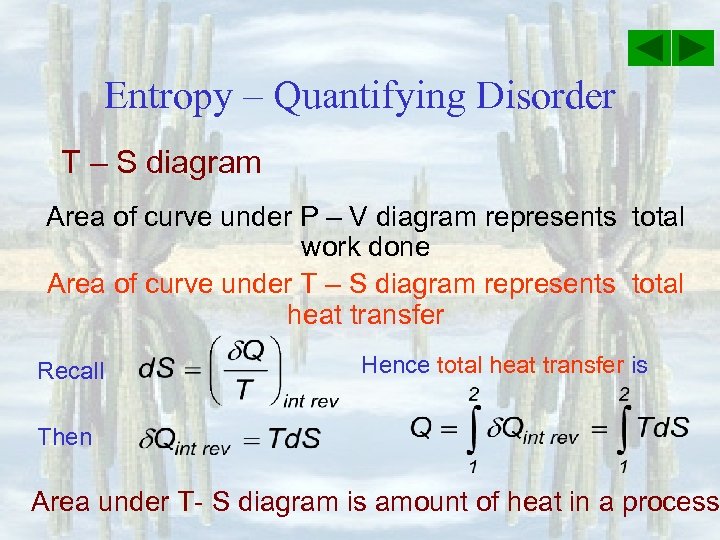Entropy – Quantifying Disorder T – S diagram Area of curve under P – V diagram represents total work done Area of curve under T – S diagram represents total heat transfer Recall Hence total heat transfer is Then Area under T- S diagram is amount of heat in a process

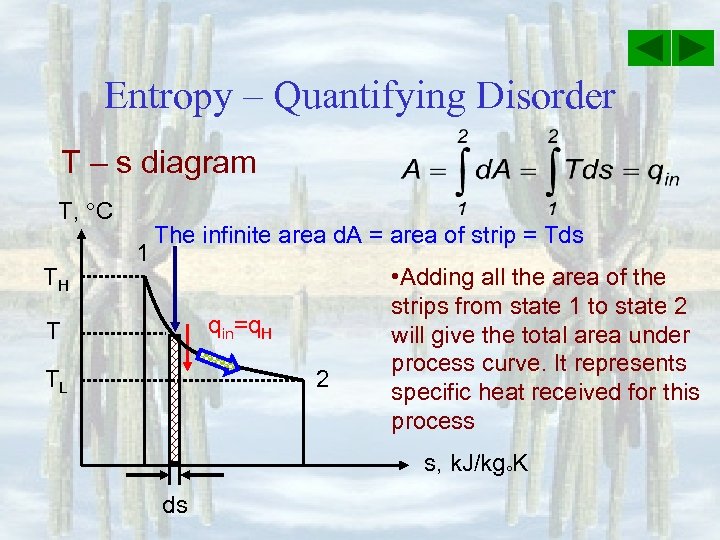Entropy – Quantifying Disorder T – s diagram T, C TH 1 The infinite area d. A = area of strip = Tds qin=q. H T TL 2 • Adding all the area of the strips from state 1 to state 2 will give the total area under process curve. It represents specific heat received for this process s, k. J/kg K ds

Entropy – Quantifying Disorder Factors affecting Entropy (disorder) ØEntropy will change when there is ØHeat transfer (receiving heat increases entropy) ØMass transfer (moving mass changes entropy) ØIrreversibilities (entropy will always be generated)

Entropy – Quantifying Disorder Entropy Balance ØFor any system undergoing any process, ØEnergy must be conserved (Ein – Eout = Esys) ØMass must be conserved (min – mout = msys) ØEntropy will always be generated except for reversible processes v. Entropy balance is (Sin – Sout + Sgen = Ssys)

Entropy – Quantifying Disorder Entropy Balance –Closed system Energy Balance: Entropy Balance:

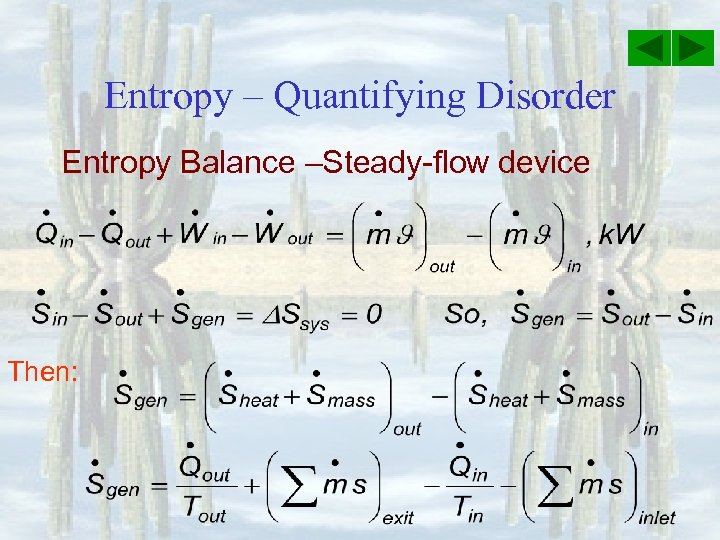Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Then:

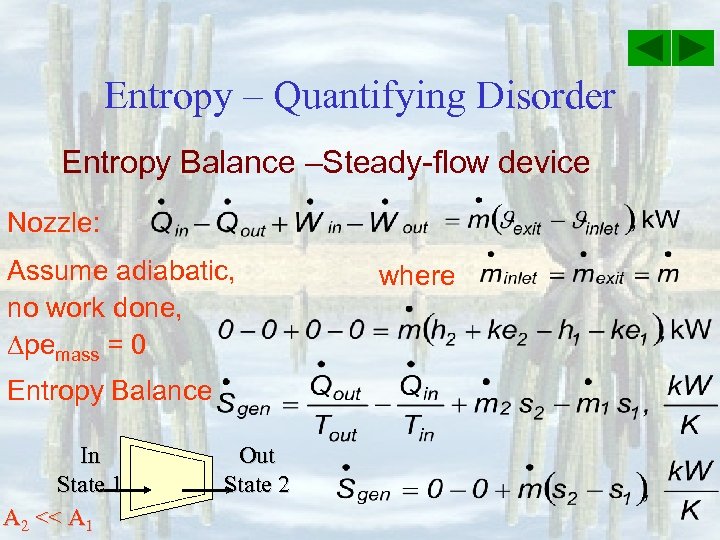Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Nozzle: Assume adiabatic, no work done, pemass = 0 Entropy Balance In State 1 A 2 << A 1 Out State 2 where

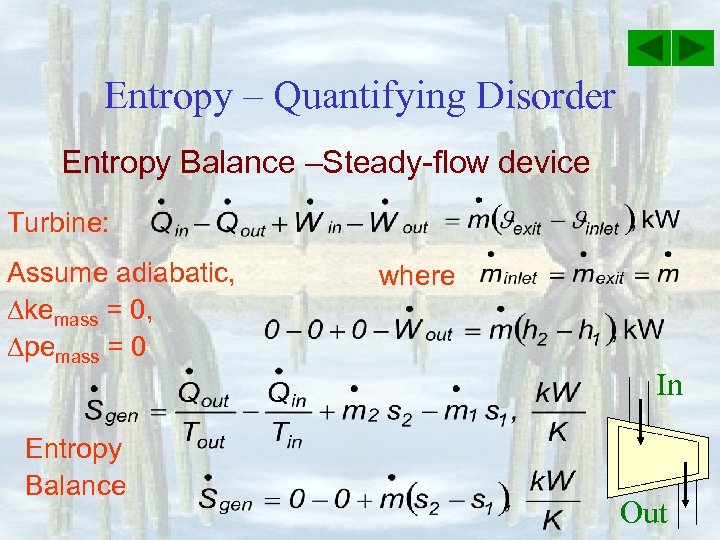Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Turbine: Assume adiabatic, kemass = 0, pemass = 0 Entropy Balance where In Out

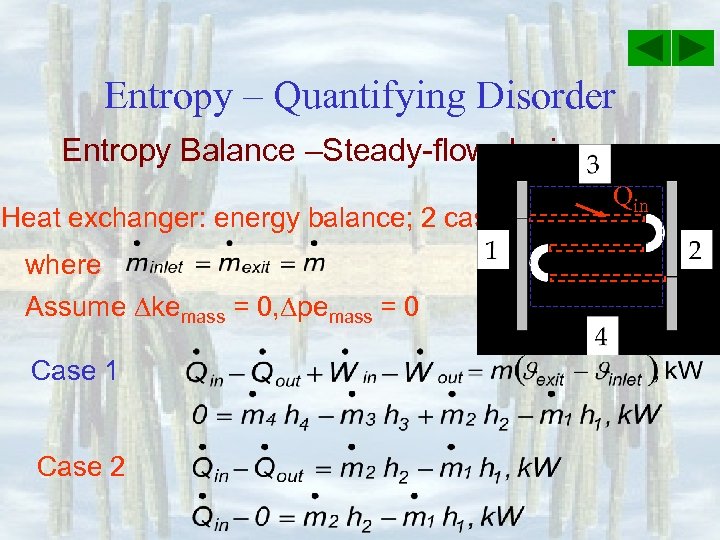Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Heat exchanger: energy balance; 2 cases where Assume kemass = 0, pemass = 0 Case 1 Case 2 Qin

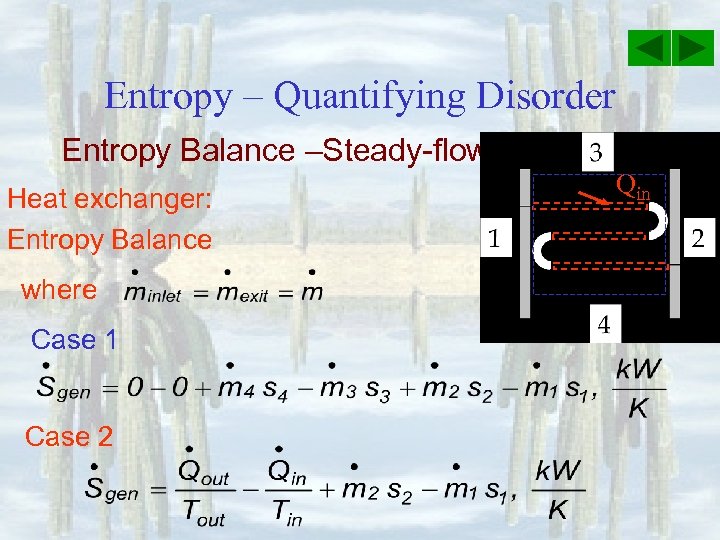Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Heat exchanger: Entropy Balance where Case 1 Case 2 Qin

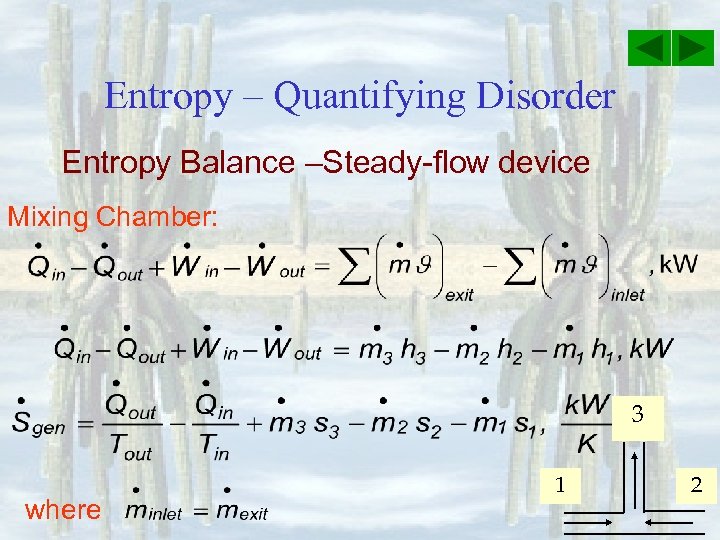Entropy – Quantifying Disorder Entropy Balance –Steady-flow device Mixing Chamber: 3 where 1 2