Thermodynamics I Te mperature Thermal Equilibrium and

Thermodynamics I Te mperature • Thermal Equilibrium and Temperature scales • Absolute Temperature Scale. The Ideal-Gas Law • The Kinetic Theory of Gases. Pressure and Temperature Heat • Heat capacity and Specific Heat • Change of Phase and Latent Heat • Thermal expansion and Phase Diagrams • Heat Transfer • Transport Laws References: Tipler; wikipedia, Britannica

Thermodynamics II The First Law of Thermodynamics • Heat and Work. First Law of Thermodynamics • Heat and Work on Quasi-Static Processes for a Gas. The Second Law of Thermodynamics • Heat Engines and the Second Law of Thermodynamics • Refrigerators and the Second Law of Thermodynamics • The Carnot Engine • Heat Pumps • Irreversibility and disorder. Entropy References: Tipler; wikipedia, …

Temperature Thermal Equilibrium and Temperature scales Our sense of touch can usually tell us if an object is hot or cold. Usually we need get in touch –physical contact- to appreciate if a body is hot or cold. But our perception is very subjective. Temperature: measure of hotness and coldness in terms of any arbitrary scales and indicating the direction which energy spontaneously flows (from a hotter body to a colder one) A thermometer is any of class of instrument that measures the temperature. Temperature is the physical magnitude that is measured by thermometers. A physical property that changes with the temperature is called a thermometric property - most solids an liquids expand when they are heated - electrical resistance change when is heated - in a gas pressure and volume change when it is heated - radiation from the surface of a body -…… References: Tipler; Britannica

Temperature • Thermal Equilibrium and Temperature scales Thermal contact Thermal equilibrium If two objects are in thermal equilibrium with a third, then they are in thermal equilibrium each other (Zeroth Law of thermodynamics) Two objects are defined to have the same temperature if they are in thermal equilibrium with each other. Temperature may be defined as the property of a system that determines whether it is in thermal equilibrium with other system. Temperature is one of the seven basic physical quantities in term of which all other physical quantities are defined. It is an “intensive” property, as pressure or density. Length, mass are “extensive”

Temperature • Thermal Equilibrium and Temperature scales Thermal contact Thermal equilibrium If two objects are in thermal equilibrium with a third, then they are in thermal equilibrium each other (Zeroth Law of thermodynamics) Two objects are defined to have the same temperature if they are in thermal equilibrium with each other

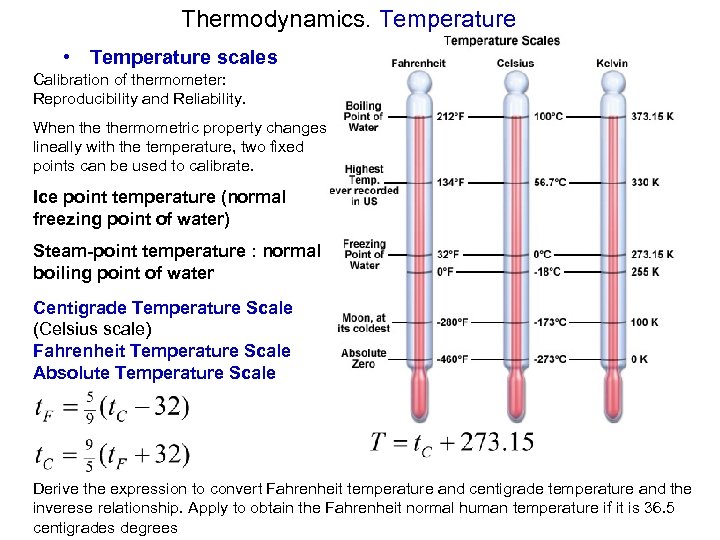
Thermodynamics. Temperature • Temperature scales Calibration of thermometer: Reproducibility and Reliability. When thermometric property changes lineally with the temperature, two fixed points can be used to calibrate. Ice point temperature (normal freezing point of water) Steam-point temperature : normal boiling point of water Centigrade Temperature Scale (Celsius scale) Fahrenheit Temperature Scale Absolute Temperature Scale Derive the expression to convert Fahrenheit temperature and centigrade temperature and the inverese relationship. Apply to obtain the Fahrenheit normal human temperature if it is 36. 5 centigrades degrees

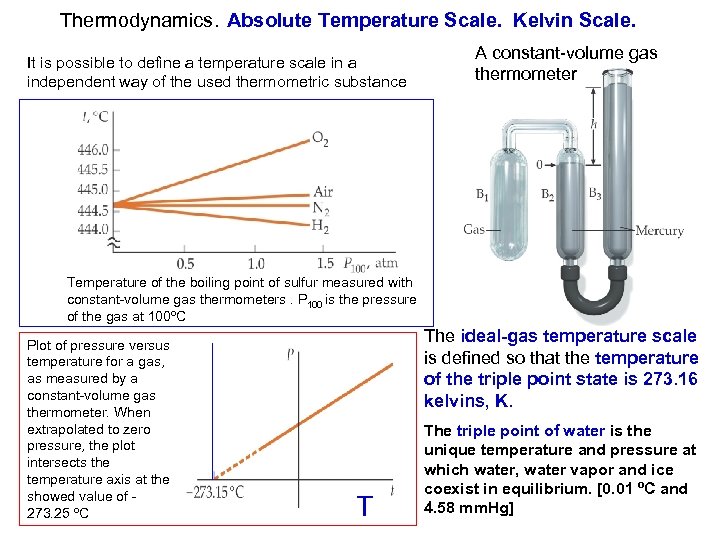
Thermodynamics. Absolute Temperature Scale. Kelvin Scale. It is possible to define a temperature scale in a independent way of the used thermometric substance A constant-volume gas thermometer Temperature of the boiling point of sulfur measured with constant-volume gas thermometers. P 100 is the pressure of the gas at 100ºC Plot of pressure versus temperature for a gas, as measured by a constant-volume gas thermometer. When extrapolated to zero pressure, the plot intersects the temperature axis at the showed value of - 273. 25 ºC The ideal-gas temperature scale is defined so that the temperature of the triple point state is 273. 16 kelvins, K. T The triple point of water is the unique temperature and pressure at which water, water vapor and ice coexist in equilibrium. [0. 01 ºC and 4. 58 mm. Hg]

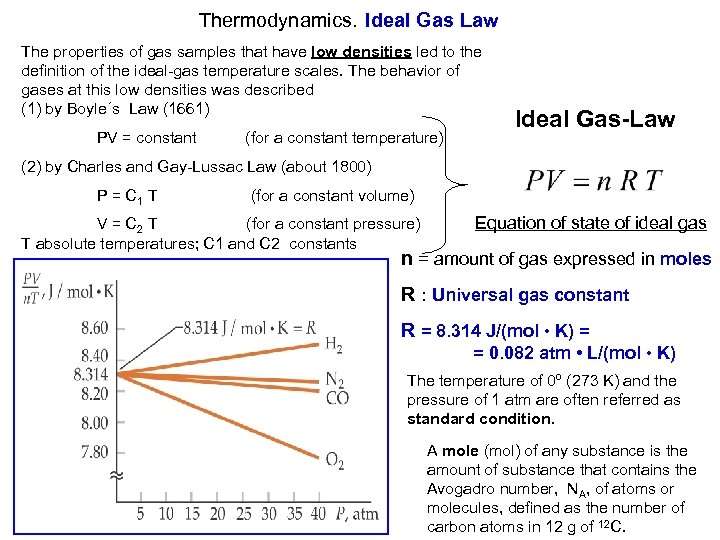
Thermodynamics. Ideal Gas Law The properties of gas samples that have low densities led to the definition of the ideal-gas temperature scales. The behavior of gases at this low densities was described (1) by Boyle´s Law (1661) PV = constant (for a constant temperature) Ideal Gas-Law (2) by Charles and Gay-Lussac Law (about 1800) P = C 1 T (for a constant volume) Equation of state of ideal gas V = C 2 T (for a constant pressure) T absolute temperatures; C 1 and C 2 constants n = amount of gas expressed in moles R : Universal gas constant R = 8. 314 J/(mol • K) = = 0. 082 atm • L/(mol • K) The temperature of 0º (273 K) and the pressure of 1 atm are often referred as standard condition. A mole (mol) of any substance is the amount of substance that contains the Avogadro number, NA, of atoms or molecules, defined as the number of carbon atoms in 12 g of 12 C.

Thermodynamics. Dealing with the Ideal Gas Law Ideal Gas-Law Equation of state of ideal gas n = m/ M [mass of the substance in g/molecular mass] mol R = 8. 314 J/(mol • K) = 0. 082 atm • L/(mol • K) The mass per mole of a substance is called its molar mass. (The terms molecular mass or molecular weight are sometimes used A gas has a volume of 2 L, a temperature of 30ºC, and a pressure of 1 atm. When the gas is heated to 60ºC and compressed to a volume of 1. 5 L, what is the new pressure What is the density of dry air at standard conditions of pressure and temperature? . The same at 20ºC; The same at 20ºC and 933 mb. Molecular mass: 28. 97 g. Answer: 1. 292 kg/m 3; 1. 204 kg/m 3; 1. 103 kg/m 3 An automobile tire is filled to a gauge pressure of 200 k. Pa when its temperature is 20ºC. After the car has been driven at high speeds, the tire temperature increases to 50ºC. (a) Assuming that the tire volumen does not change, find the gauge pressure in the tire (b) Calculate the gauge pressure if the volume of the tire expands by 10%.

Thermodynamics. The Kinetic Theory of Gases. Molecular Interpretation of Pressure and Temperature Goal : To relate macroscopic point of view abot pressure and temperature with the microscopic motion. For a solid, these microscopic motions are principally the vibrations of its atoms about their sites in the solid. For an ideal monatomic gas, the microscopic motions are the translational motions of the constituent gas particles. For a multiatomic gas, vibrational and rotational motion should be included too. The kinetic theory of gases is able us to establish quantitatively this relationship for gases The pressure that a gas exerts on its container is due to collisions between gas molecules and the container walls. This pressure is a force per unit of area and, by Newton´s second law, this force is the rate of change of momentum of the gas molecules colliding with the walls. The absolute temperature is a measure of the average translational kinetic energy of the molecules. References Tipler, Chapter 17 http: //en. wikipedia. org/wiki/Kinetic_theory#Pressure http: //en. wikipedia. org/wiki/Temperature http: //en. wikipedia. org/wiki/Image: Translational_motion. gif

Thermodynamics I Te mperature • Thermal Equilibrium and Temperature scales • Absolute Temperature Scale. The Ideal-Gas Law • The Kinetic Theory of Gases. Pressure and Temperature Heat • Heat capacity and Specific Heat • Change of Phase and Latent Heat • Thermal expansion and Phase Diagrams • Heat Transfer • Transport Laws References: Tipler; wikipedia, Britannica

Thermodynamics. Heat capacity and Specific Heat is the energy that is being transferred from one system to another as a result of difference in temperature. If two bodies at different temperature are brought together, energy is transferred –i. e. heat flows- from the hotter body to the colder. The effect of this transfer of energy usually, but non always*, is an increase in the temperature of the colder body and an decrease of the hotter body; the amount of heat that leaves one equals the amount that enters the other. Heat Capacity and Specific Heat The amount of heat energy Q needed to raise the temperature of a substance is proportional to the temperature change and to the mass of substance. Units of heat: Calorie [cal] : the amount of cwater: 1 cal/(g • ºC)= 1 kcal/(kg • ºC)= energy to be transferred to raise the temperature 4. 184 k. J/(kg • ºC) = 4. 184 k. J/(kg • K) of one gram of water one centigrade degree. 1 cal = 4. 184 J The heat capacity per mole is called the molar specific heat * The exceptions occurs during a change of phase

Thermodynamics. Heat capacity and Specific Heat is the energy that is being transferred from one system to another as a result of difference in temperature. If two bodies at different temperature are brought together, energy is transferred –i. e. heat flows- from the hotter body to the colder. The effect of this transfer of energy usually, but non always*, is an increase in the temperature of the colder body and an decrease of the hotter body; the amount of heat that leaves one equals the amount that enters the other. Heat Capacity and Specific Heat The amount of heat energy Q needed to raise the temperature of a substance is proportional to the temperature change and to the mass of substance. cwater: 1 cal/(g • ºC)= 1 kcal/(kg • ºC)= Units of heat: Calorie [cal] : the amount of energy to be transferred to raise the temperature 4. 184 k. J/(kg • ºC) = 4. 184 k. J/(kg • K) of one gram of water one centigrade degree. 1 cal = 4. 184 J The heat capacity per mole is The specific heat of a substance depends of the way as the heat is transferred. The most commonly determined specific heats are the specific heat at constant pressure and the specific heat at constant volume called the molar specific heat * The exceptions occurs during a change of phase

Thermodynamics. Change of Phase and Latent Heat Common types of phase change include fusion (liquid to solid), melting (solid to liquid), vaporization (liquid to vapor or gas); condensation (gas or vapor to liquid), and sublimation (solid directly to vapor). When a phase change appears there is no temperature change when thermal energy is being transferred to the body in which the phase change is occurring. In the case of a phase change the specific heat (or capacity) is infinitum. Latent Heat Latent heat of fusion, Lf. At a pressure of 1 atm, the latent heat of fusion for water Lf =333. 5 KJ/kg Latent heat of vaporization, LV. For water at a pressure of 1 atm, the latent heat of vaporization is Lf = 2. 25 MJ/kg. Latent heat depends on the temperature. The value of

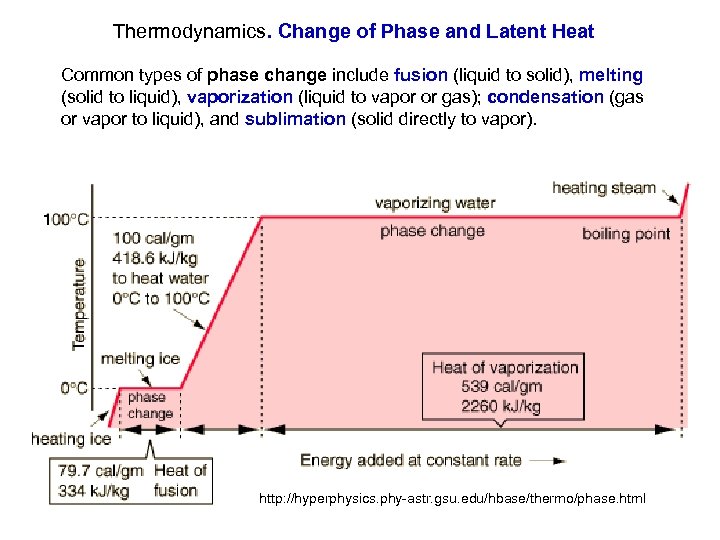
Thermodynamics. Change of Phase and Latent Heat Common types of phase change include fusion (liquid to solid), melting (solid to liquid), vaporization (liquid to vapor or gas); condensation (gas or vapor to liquid), and sublimation (solid directly to vapor). http: //hyperphysics. phy-astr. gsu. edu/hbase/thermo/phase. html

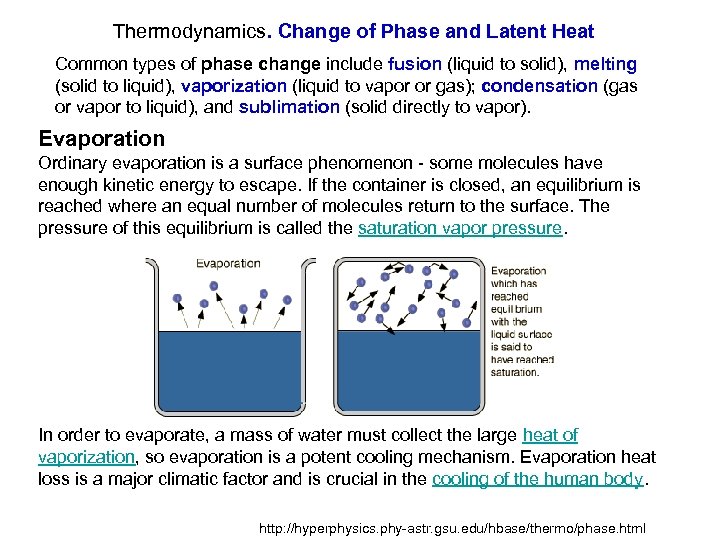
Thermodynamics. Change of Phase and Latent Heat Common types of phase change include fusion (liquid to solid), melting (solid to liquid), vaporization (liquid to vapor or gas); condensation (gas or vapor to liquid), and sublimation (solid directly to vapor). Evaporation Ordinary evaporation is a surface phenomenon - some molecules have enough kinetic energy to escape. If the container is closed, an equilibrium is reached where an equal number of molecules return to the surface. The pressure of this equilibrium is called the saturation vapor pressure. In order to evaporate, a mass of water must collect the large heat of vaporization, so evaporation is a potent cooling mechanism. Evaporation heat loss is a major climatic factor and is crucial in the cooling of the human body. http: //hyperphysics. phy-astr. gsu. edu/hbase/thermo/phase. html

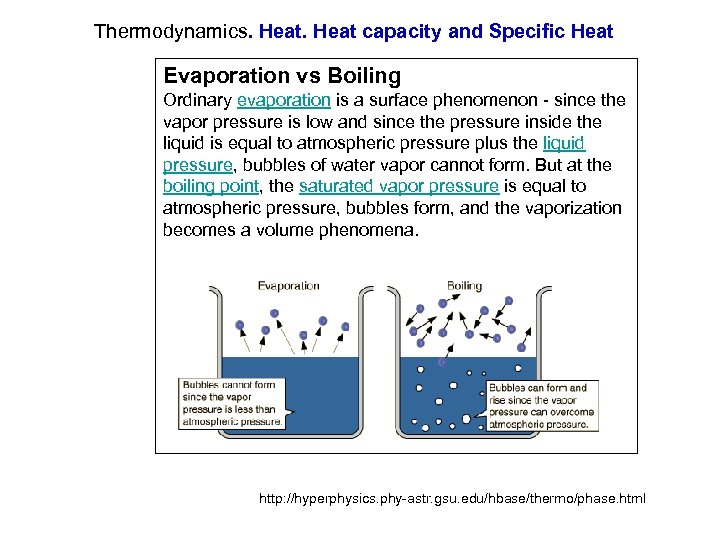
Thermodynamics. Heat capacity and Specific Heat Evaporation vs Boiling Ordinary evaporation is a surface phenomenon - since the vapor pressure is low and since the pressure inside the liquid is equal to atmospheric pressure plus the liquid pressure, bubbles of water vapor cannot form. But at the boiling point, the saturated vapor pressure is equal to atmospheric pressure, bubbles form, and the vaporization becomes a volume phenomena. http: //hyperphysics. phy-astr. gsu. edu/hbase/thermo/phase. html

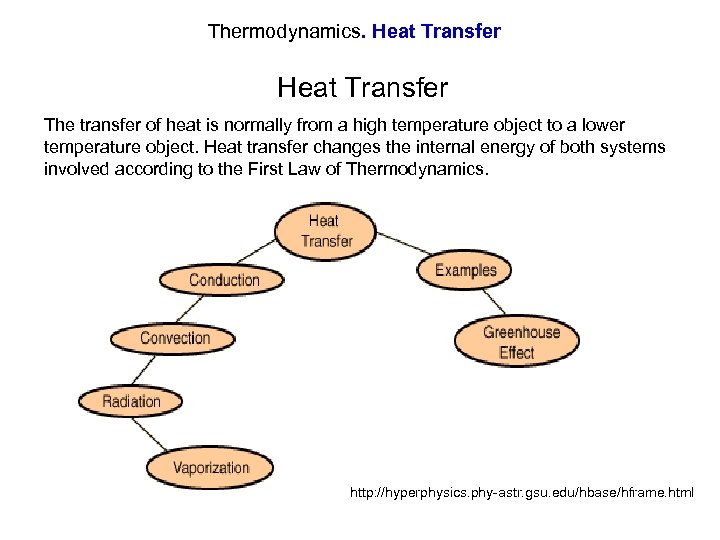
Thermodynamics. Heat Transfer The transfer of heat is normally from a high temperature object to a lower temperature object. Heat transfer changes the internal energy of both systems involved according to the First Law of Thermodynamics. http: //hyperphysics. phy-astr. gsu. edu/hbase/hframe. html

Thermodynamics. Heat Transfer Heat Conduction is heat transfer by means of molecular agitation within a material without any motion of the material as a whole. If one end of a metal rod is at a higher temperature, then energy will be transferred down the rod toward the colder end because the higher speed particles will collide with the slower ones with a net transfer of energy to the slower ones. For heat transfer between two plane surfaces, such as heat loss through the wall of a house, the rate of conduction heat transfer is: Calculation = area = thermal conductivity of the barrier = temperature = heat transferred in time = = thickness of barrier http: //hyperphysics. phy-astr. gsu. edu/hbase/hframe. html