THERMOCHEMISTRY Concept of Enthalpy Important Terms

THERMOCHEMISTRY

Concept of Enthalpy

Important Terms n Heat is energy transferred between two bodies of different temperatures n System is any specific part of the universe n Surroundings is everything that lies outside the system

n Open system is a system that can exchange mass and energy with its surroundings n Closed system is a system that allows the exchange of energy with its surroundings n Isolated system is a system that does not allow the exchange of either mass or energy with its surroundings

n Energy is the ability to do work n n n SI unit of energy is kg m 2 s-2 or Joule (J) Non SI unit of energy is calorie (Cal) 1 Cal = 4. 184 J

Thermochemistry A study of heat change in chemical reactions. n Two types of chemical reactions: n n n Exothermic Endothermic

Exothermic reactions Enthalpy of products < Enthalpy of reactants, ΔH is negative. Energy is released from the system to the surroundings.

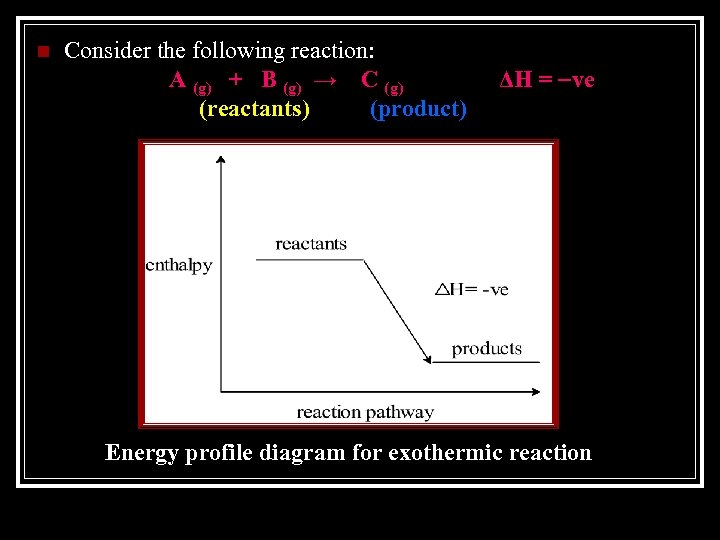n Consider the following reaction: A (g) + B (g) → C (g) (reactants) (product) ΔH = ve Energy profile diagram for exothermic reaction

Endothermic Reactions n Enthalpy of products > enthalpy of reactants, ΔH is positive n Energy is absorbed by the system from the surrounding

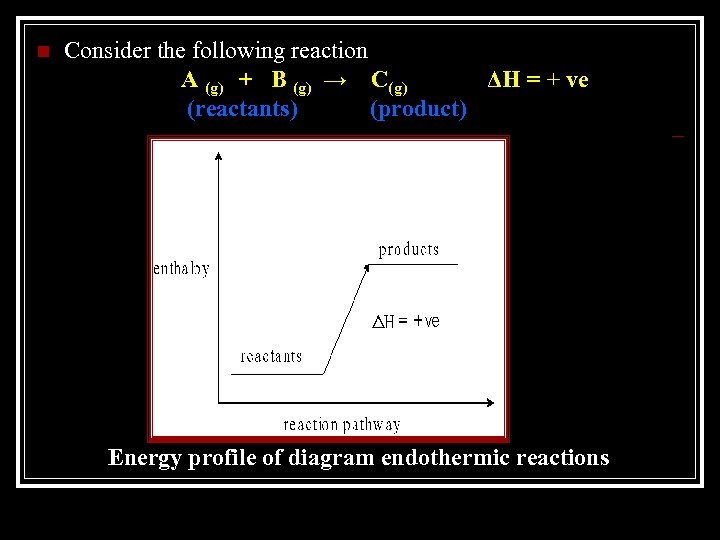n Consider the following reaction A (g) + B (g) → C(g) ΔH = + ve (reactants) (product) Energy profile of diagram endothermic reactions

Enthalpy, H n The heat content of a system or total energy in the system n Enthalpy, H of a system cannot be measured when there is a change in the system. n Example: system undergoes combustion or ionisation.

Enthalpy of Reaction, ∆H and Standard Condition n Enthalpy of reaction: n The enthalpy change associated with a chemical reaction. n Standard enthalpy, ∆Hº n The enthalpy change for a particular reaction that occurs at 298 K and 1 atm (standard state)

Thermochemical Equation n The thermochemical equation shows the enthalpy changes. Example : H 2 O(s) → H 2 O(l) ΔH = +6. 01 k. J n 1 mole of H 2 O(l) is formed from 1 mole of H 2 O(s) at 0°C, ΔH = +6. 01 k. J n However, when 1 mole of H 2 O(s) is formed from 1 mole of H 2 O(l), the magnitude of ΔH remains the same with the opposite sign of it. H 2 O(l) → H 2 O(s) ΔH = 6. 01 k. J

Types of Enthalpies n There are many kind of enthalpies such as: n Enthalpy of formation n Enthalpy of combustion n Enthalpy of atomisation n Enthalpy of neutralisation n Enthalpy of hydration n Enthalpy of solution n Enthalphy of sublimation

Enthalpy of Formation, ∆Hf n The change of heat when 1 mole of a compound is formed from its elements at their standard states. H 2 (g) + ½ O 2(g) → H 2 O (l) n ∆Hf = 286 k. J mol 1 The standard enthalpy of formation of any element in its most stable state form is ZERO. ∆H (O 2 ) = 0 ∆H (Cl 2) = 0

Enthalpy of Combustion, ∆Hc n The heat released when 1 mole of substance is burned completely in excess oxygen. C(s) + O 2(g) → CO 2(g) ∆Hc = 393 k. J mol 1

Enthalpy of Atomisation, Ha n The heat change when 1 mole of gaseous atoms is formed from its element n Ha is always positive because it involves only breaking of bonds e. g: n Na(s) Na(g) Ha = +109 k. J mol-1 ½Cl 2(g) Cl(g) Ha = +123 k. J mol-1

Enthalpy of Neutralization, ∆Hn n The heat change when 1 mole of water, H 2 O is formed from the neutralization of acid and base. n HCl(aq)+ Na. OH(aq) → Na. Cl(aq) +H 2 O(aq) ΔHn = 58 k. J mol 1

Enthalpy of Hydration, Hhyd n n The heat change when 1 mole of gaseous ions is hydrated in water. e. g: Na+(g) Na+(aq) Hhyd = 406 k. J mol-1 Cl-(g) Cl-(aq) Hhyd = 363 k. J mol-1

Enthalpy of Solution, Hsoln The heat change when 1 mole of a substance is dissolves in water. n e. g: KCl(s) K+(aq) + Cl (aq) Hsoln = +690 k. J mol-1

Enthalpy of Sublimation, Hsubl The heat change when one mole of a substance sublimes (solid into gas). I 2 (s) → I 2(g) Hsubl = +106 k. J mol 1

Calorimetry A method used in the laboratory to measure the heat change of a reaction. n Apparatus used is known as the calorimeter n Examples of calorimeter n n n Simple calorimeter Bomb calorimeter

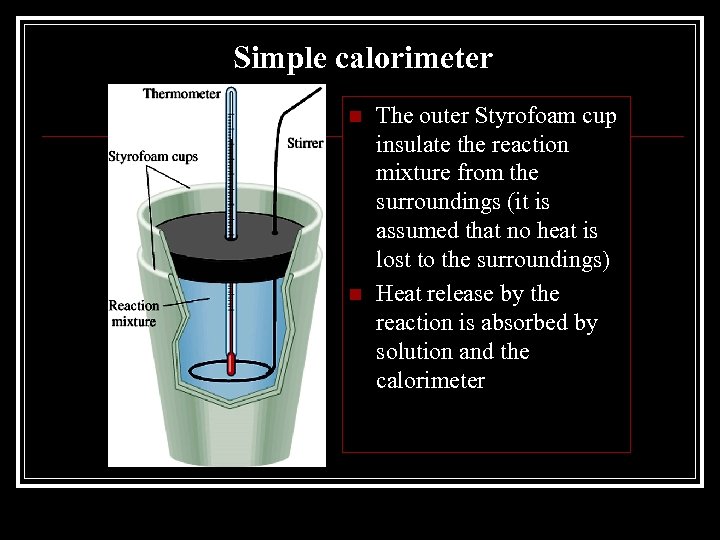Simple calorimeter n n The outer Styrofoam cup insulate the reaction mixture from the surroundings (it is assumed that no heat is lost to the surroundings) Heat release by the reaction is absorbed by solution and the calorimeter

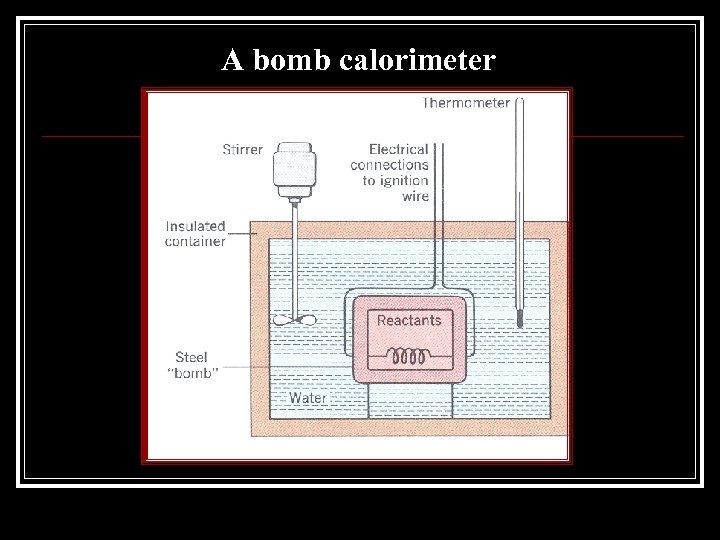A bomb calorimeter

Important Terms in Calorimeter n n Specific heat capacity, c of a substance is the amount of heat required to raise the temperature of one gram of the substance by one degree Celsius (Jg 1 C 1). Heat capacity, C n Heat capacity, C is the amount of heat required to raise the temperature of a given quantity of the substance by one degree Celsius (J C 1)

Heat released by substance = Heat absorbed by calorimeter q = mc∆T q = heat released by substance m= mass of substance C= specific heat capacity ∆T = temperature change

Basic Principle in Calorimeter Heat released by a reaction = Heat absorbed by surroundings • Surroundings may refer to the: i. Calorimeter itself or; ii. The water and calorimeter • qreaction= mcΔT or CΔT

Example 1 In an experiment, 0. 100 g of H 2 and excess of O 2 were compressed into a 1. 00 L bomb and placed into a calorimeter with heat capacity of 9. 08 x 104 J 0 C 1. The initial temperature of the calorimeter was 25. 0000 C and finally it increased to 25. 155 0 C. Calculate the amount of heat released in the reaction to form H 2 O, expressed in k. J per mole.

Solution Heat released = Heat absorbed by the calorimeter q = C∆T = (9. 08 X 104 J 0 C-1) X (0. 1550 C) = 1. 41 X 104 J = 14. 1 k. J H 2(g) + ½O 2(g) → H 2 O(c) mole of H 2 = 0. 100 2. 016 = 0. 0496 mol

moles of H 2 O = mole of H 2 0. 0496 mol of H 2 O released 14. 1 k. J energy 1 mol H 2 O released = k. J ∆Heat of reaction, ∆H = 284 k. J = - 284 k. J mol 1

Example 2 1. Calculate the amount of heat released in a reaction in an aluminum calorimeter with a mass of 3087. 0 g and contains 1700. 0 m. L of water. The initial temperature of the calorimeter is 25. 0°C and it increased to 27. 8°C.

Given: Specific heat capacity of aluminum = 0. 553 Jg-1 °C-1 Specific heat capacity of water = 4. 18 Jg-1 °C-1 Water density = 1. 0 g m. L-1 ΔT = (27. 8 -25. 0 )°C = 2. 8°C Solution Heat released = Heat absorbed by aluminium calorimeter q = mwcwΔT + mcccΔT = (1700. 0 g)(4. 18 Jg-1 °C-1)(2. 8 °C) + (3087. 0 g)(0. 553 Jg-1 °C-1)(2. 8°C) = 24676. 71 J = 24. 7 k. J + Heat absorbed by water

HESS’S LAW

Hess Law n n Hess’s Law states that when reactants are converted to products, the change in enthalpy is the same whether the reaction takes place in one step or in the series of steps. The enthalpy change depends only on the nature of the reactants and products and is independent of the route taken. A B C

Algebraic Method Step 1 i. List all thermochemical equations involved

Algebraic Method Step 1 i. List all thermochemical equations involved

ii. Write the enthalpy of formation reaction for C 2 H 6

iii. Add the given reactions so that the result is the desired reaction.

Energy Cycle Method Draw the energy cycle and apply Hess’s Law to calculate the unknown value.

Example 1 The thermochemical equation of combustion of carbon monoxide is shown as below. C(s) + ½ O 2(g) CO(g) =? given : C(s) + O 2(g) CO 2(g) ∆H= -394 k. J mol-1 CO(s) + ½ O 2(g) CO 2(g) ∆H= -283 k. J mol-1 Calculate the enthalpy change of the combustion of carbon to carbon monoxide.

Example 2 Calculate the standard enthalpy of formation of methane if the enthalpy of combustion of carbon, hydrogen and methane are as follows: ∆H [C(s)] = -393 k. J mol-1 ∆H [H 2(s)] = -293 k. J mol-1 ∆H [CH 4(s)] = -753 k. J mol-1

Example 3 n Standard enthalpy of formation of ammonia, hydrogen chloride and ammonium chloride is -46. 1 k. J mol-1, -92. 3 k. J mol-1, 314. 4 k. J mol-1 respectively. Write thermochemical equation for the formation of each substance and calculate the enthalpy change for the following reaction. NH 3(g) + HCl (g) NH 4 Cl(s)

Exercise 1. Calculate the enthalpy of formation of benzene if : ∆H (CO 2(g) ) = -393. 3 k. J mol-1 ∆H (H 2 O(l) ) = -285. 5 k. J mol-1 ∆H (C 6 H 6(l) ) = -3265. 3 k. J mol-1

Born-Haber Cycle

Lattice Energy, Hlattice n is the energy required to completely separate one mole of a solid (ionic compound) into gaseous ions e. g: Na. Cl(s) Na+(g) + Cl-(g) n Na+(g) + Cl-(g) Na. Cl(s) n Hlattice = +771 k. J mol-1 (lattice dissociation) Hlattice = -771 k. J mol-1 (lattice formation) The magnitude of lattice energy increases as n the ionic charges increase n the ionic radii decrease

n There is a strong attraction between small ions and highly charged ions so the H is more negative. n H for Mg. O is more negative than H for Na 2 O because Mg 2+ is smaller in size and has bigger charge than Na+, therefore Hºlattice (Mg. O) > Hºlattice (Na 2 O)

Hydration Process of Ionic Solid n Na+ and Cl- ions in the solid crystal are separated from each other and converted to the gaseous state ( Hlattice) n The electrostatic forces between gaseous ions and polar water molecules cause the ions to be surrounded by water molecules ( Hhydr) Hsoln = Hlattice + Hhdyr

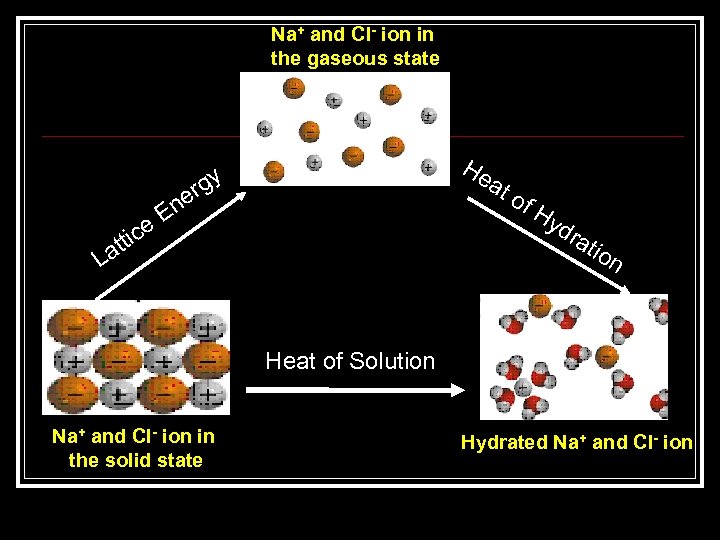Na+ and Cl- ion in the gaseous state ttic La er En e He gy at of Hy dra tio n Heat of Solution Na+ and Cl- ion in the solid state Hydrated Na+ and Cl- ion

Born-Haber Cycle n n The process of ionic bond formation occurs in a few stages. At each stage the enthalpy changes are considered. The Born Haber cycle is often used to calculate the lattice energy of an ionic compound. In the Born-Haber cycle energy diagram, by convention, positive values are denoted as going upwards, negative values as going downwards. Consider the enthalpy changes in the formation of sodium chloride.

Example : n i. iii. iv. v. vi. Given; Enthalpy of formation Na. Cl Enthalpy of sublimation of Na First ionization energy of Na Enthalpy of atomization of Cl Electron affinity of Cl Lattice energy of Na. Cl = = = -411 k. Jmol-1 +108 k. Jmol-1 +500 k. Jmol-1 +122 k. Jmol-1 -364 k. Jmol-1 ?

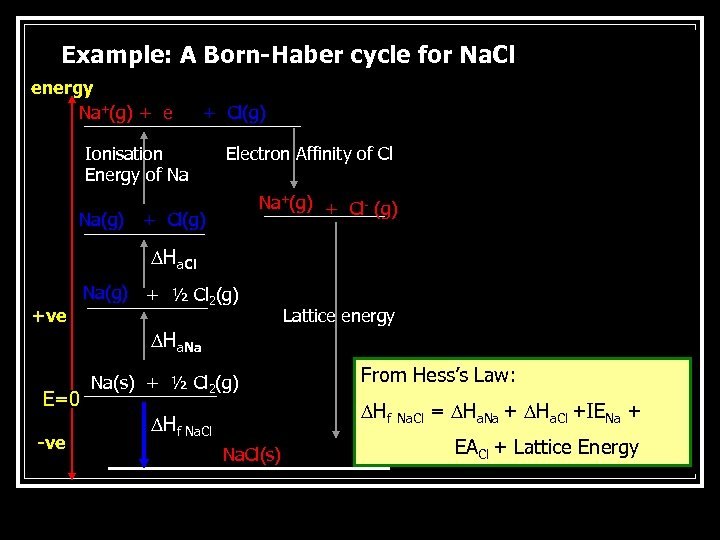Example: A Born-Haber cycle for Na. Cl energy Na+(g) + e + Cl(g) Ionisation Energy of Na Na(g) Electron Affinity of Cl Na+(g) + Cl- (g) + Cl(g) Ha. Cl +ve Na(g) + ½ Cl 2(g) Lattice energy Ha. Na E=0 -ve Na(s) + ½ Cl 2(g) From Hess’s Law: Hf Na. Cl(s) Na. Cl = Ha. Na + Ha. Cl +IENa + EACl + Lattice Energy

Calculation:

Exercise: n i. iii. iv. v. vi. Construct a Born-Haber cycle to explain why ionic compound Na. Cl 2 cannot form under standard conditions. Use the data below: Enthalpy of sublimation of sodium = +108 k. Jmol-1 First ionization energy of sodium = +500 -1 k. Jmol Second ionization energy of sodium = +4562 k. Jmol-1 Enthalpy of atomization of chlorine = +121 k. Jmol-1 Electron affinity of chlorine = -364 k. Jmol-1 Lattice energy of Na. Cl 2 = -2489 k. Jmol-1