Thermal physics Week 1 Vocabulary Understand

Thermal physics

Week 1

Vocabulary Understand these words: solid, liquid, gas, melt, freeze, boil, evaporate, condense, compress, particle, atom, molecule, pressure, volume, temperature, isothermal(ly), inverse proportion

Heat vs Temperature Heat is energy that moves from one object to another. Temperature is the measure of how hot something is. It is a measure of the average kinetic energy of the molecules of something. Heat travels from an area of high temperature to an area of low temperature.

Average Kinetic Energy Temperature is a measure of the average kinetic energy of all molecules. Ke = ½ mv 2 All molecules do not have the same mass so they do not have the same velocity. Heavier molecules have a slower average velocity.

Objective 1 recall and understand the terms mean-square velocity, saturated and unsaturated vapors, surface tension, capillary effect;

mean-square velocity Root-mean-square speed is defined as the square root of the average velocitysquared of the molecules in a gas. It is given by the formula

Boltzmann Equation 8

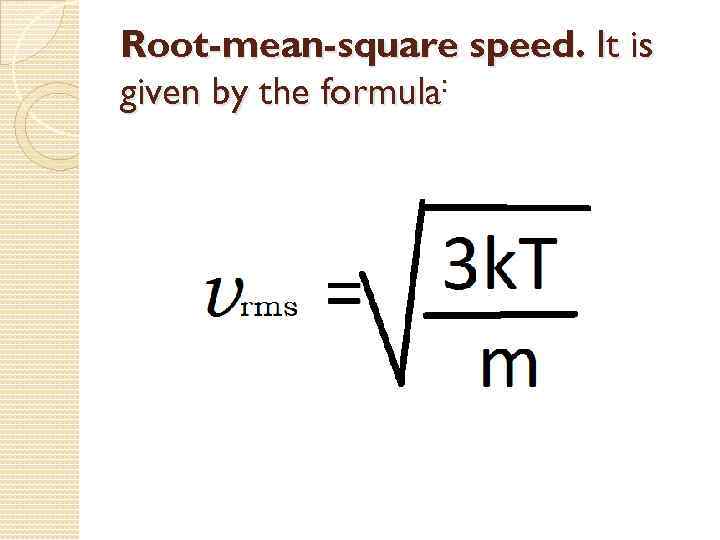
Root-mean-square speed. It is given by the formula:

K is the Boltzmann constant = R/N T is temperature in Kelvin R is the gas constant

Sample Problems Four molecules have speeds 300 m/s, 350 m/s, 380 m/s and 500 m/s. Find the average speed and the root mean square speed. 11

Why use Vrms? What is the average velocity of the molecules of a gas?

http: //www. youtube. com/watc h? v=KC 3 lx 1 Twx. Ks

Vapor pressure or equilibrium vapor pressure is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system.

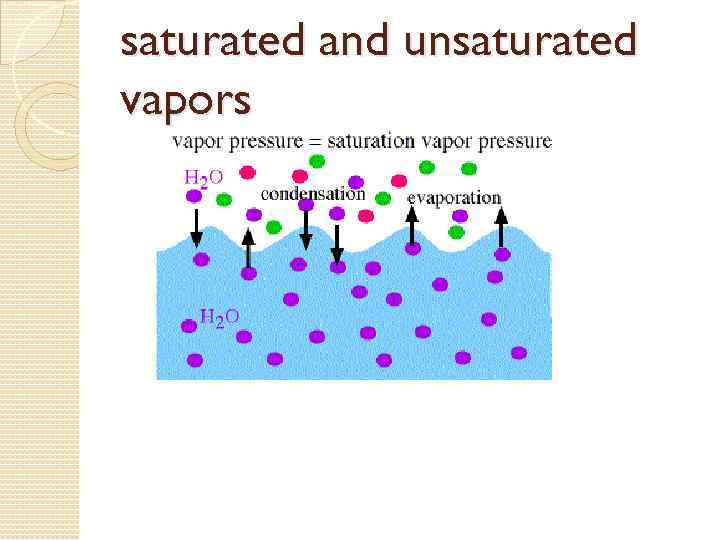
saturated and unsaturated vapors

Surface Tension Surface tension is a contractive tendency of the surface of a liquid that allows it to resist an external force.

Capillary Effect Capillary effect, is the ability of a liquid to flow in narrow spaces without the assistance of, and in opposition to external forces like gravity

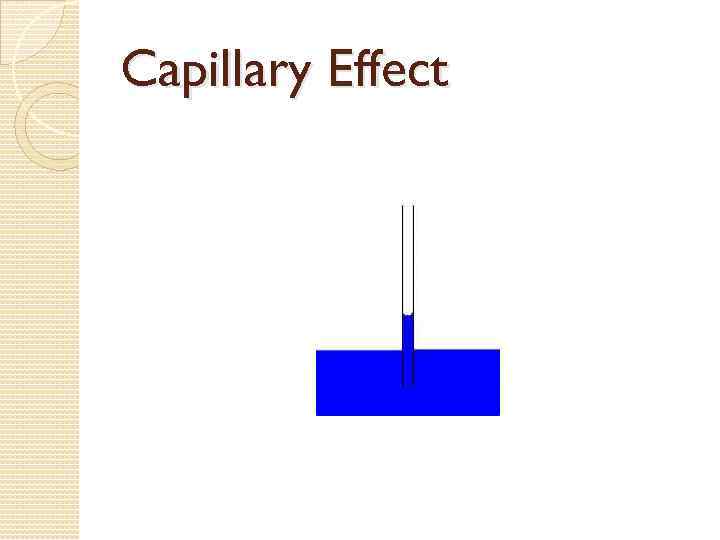
Capillary Effect

Stop for demonstrations

Objective 2 recall and understand laws of ideal gas and Dalton’s law;

Ideal Gas The idea of Ideal Gas allow us to do math to model physical properties

Dalton's Law of Partial Pressure. states that the pressure of a gas mixture is the sum of the partial pressures of the individual components of the gas mixture.

Partial Pressures The sum of the pressures of individual gasses equals the total pressure P 1 +P 2+ P 3…. +PN = Ptotal

Objectives 3 & 4 describe kinetic model and model of ideal gas; recall principles of kinetic model

Importance of Kinetic Theory of Gases Recall that temperature is a measure of the kinetic energy of the molecules in a material. But it would be impossible to study their behavior individually since molecules are very small and there are so many molecules in most substances. 28

Importance of Kinetic Theory of Gases Recall that temperature is a measure of the kinetic energy of the molecules in a material. But it would be impossible to study their behavior individually since molecules are very small and there are so many molecules in most substances. 29

Basic assumptions of the kinetic theory of gasses 1. A gas contains of a large number of molecules. 2. Molecules move with a range of speeds. 3. The volume of the molecules is negligible compared with the volume of the gas itself. 30

Basic assumptions of the kinetic theory of gasses 4. The collisions of the molecules with each other and the container walls are elastic. 5. Molecules exert no forces on each other or the container except when in contact. 31

Basic assumptions of the kinetic theory of gasses The duration of collisions is very small compared with the time between collisions. 7. The molecules obey Newton’s Laws of Motion. 6. 32

Equation of State PV = n. RT A. k. a. the Ideal Gas Law: P×V = n×R×T ◦P is pressure (in Pascal, Pa) ◦V is volume (in meters cubed, m 3) ◦n is the amount (in moles, mol)* ◦R is the ideal gas constant (8. 31 J/mol/K) ◦T is the temperature (in Kelvin, K) *1 mole equals 6. 02 × 1023 atoms

n and R are constants

Week 2

Objective 5 explain how molecular movement causes the pressure exerted by a gas and hence deduce the relationship: Go to Physics factsheet #25

Motion of Molecules and Pressure Consider an air tight container that is filled with air. How do the air molecules exert a pressure? 3 7

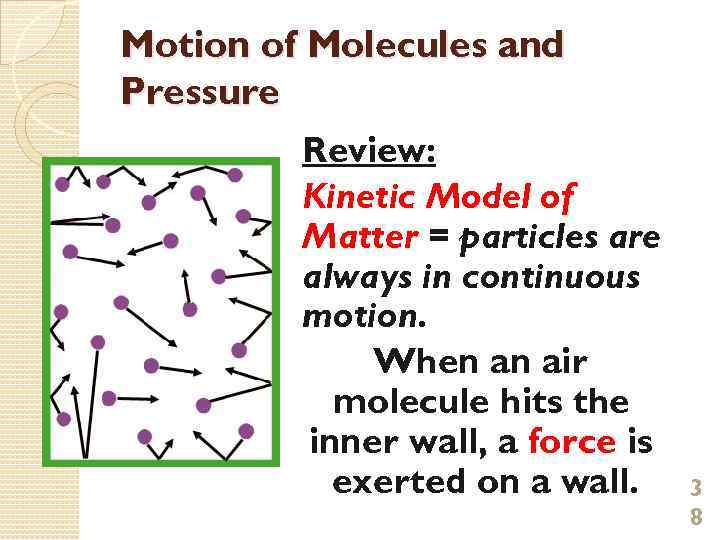
Motion of Molecules and Pressure Review: Kinetic Model of Matter = particles are always in continuous motion. When an air molecule hits the inner wall, a force is exerted on a wall. 3 8

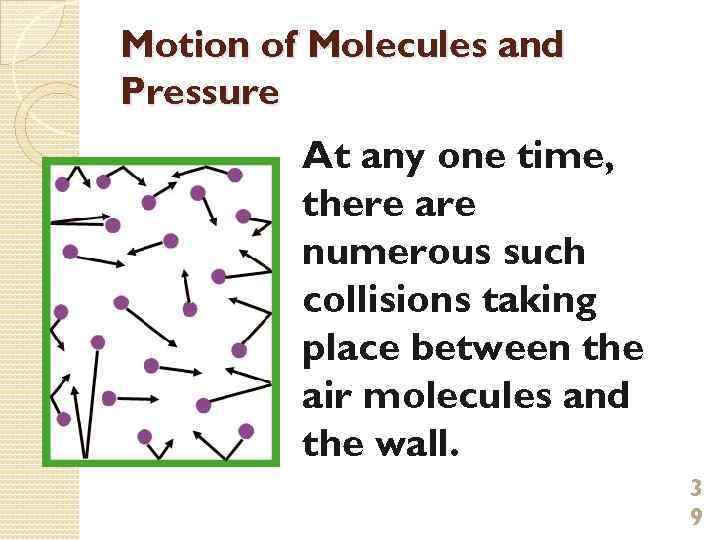
Motion of Molecules and Pressure At any one time, there are numerous such collisions taking place between the air molecules and the wall. 3 9

Motion of Molecules and Pressure average of all forces from such collisions = average force that is acting on the wall 4 0

Motion of Molecules and Pressure Recall: Pressure = force per unit area (P = F/A) Gas molecules are exerting a pressure on a container’s wall. 4 1

Motion of Molecules and Pressure Conclusion: The pressure of a gas in a container is due to the collision of gas molecules with the walls of container (not from the collisions between molecules). 4 2

Factors that affect the pressure of gas 1. Average Molecular Speed (the higher the speed, the larger the change in momentum of the molecules and so the higher the force) 2. Frequency of Collision (the more frequent the collisions, the higher the pressure) 43

Factors that affect the pressure of gas 44

Factors that affect the pressure of gas Consider a gas that has been heated under constant volume. The molecules are moving faster on average and the frequency with which the collisions take place also increases. For both reasons (speed and frequency) the pressure the goes up. 45

Factors that affect the pressure of gas If gas is compressed isothermally, the average speed stays the same. But the distance molecules have to travel between collisions with the walls is reduced and so the frequency of collisions increases. Hence the pressure increases. 46

Sample Problem A gas is compressed slowly by a piston. Explain why the temperature of the gas will stay the same. 2. A gas is compressed rapidly by a piston. Explain why the temperature of the gas will increase. 1. 47

Objective 6 recall and solve problems using the equation of state for an ideal gas expressed as р. V = NRТ;

р. V = NRТ ◦P is pressure (in Pascal, Pa) ◦V is volume (in meters cubed, m 3) ◦n is the amount (in moles, mol)* ◦R is the ideal gas constant (8. 31 J/mol/K) ◦T is the temperature (in Kelvin, K) *1 mole equals 6. 02 × 1023 atoms

Gases To specify the quantity of a gas, it is convenient to use the number of moles (n) of the gas rather than the mass itself to specify the quantity of a gas. Recall Avogadro constant 23 molecules/mole NA = 6. 02 × 10 50

Gases 51

Sample Problems 1. The pressure of a gas is 2 atm and its volume is 0. 9 L. If the pressure is increased to 6 atm at constant temperature, what is the new volume? 52

Sample Problems 2. A gas expands at constant pressure from an original volume of 2 L at 22°C to a volume of 4 L. What is the new temperature? 53

Sample Problems 3. A gas in a container of fixed volume is heated from a temperature of 20°C and pressure of 3 atm to a temperature of 85°C. What is the new pressure? 54

Sample Problems 1. How many moles of gas are there in a gas of temperature 300 K, volume 0. 02 m 3 and 5 Pa? pressure 2 × 10 55

Sample Problems 2. A container of hydrogen 3 and of volume 0. 1 m temperature 25°C contains 3. 20 × 1023 molecules. What is the pressure in the container? 56

Sample Problems 3. A gas of volume 2 L, pressure 3 atm and temperature 300 K expands to a volume of 3 L and a pressure of 4 atm. What is the new temperature of the gas? 57

Objective 7 Compare and p. V = Nkt and hence deduce that the average translational kinetic energy of a molecule is proportional to T;

Boltzmann Equation 59

Watch this clip http: //www. youtube. com/watc h? v=Yz. HWt 9 QT 98 s

Week 3

Objective 8 describe changes in volume due to pressure with constant temperature (Law of Boyle. Mariotte);

The Boyle-Mariotte Law (Boyle’s Law) Boyle’s Law relates pressure and volume for a gas fixed temperature. Boyle’s Law for gases states that the pressure of a fixed mass of gas is inversely proportional to its volume at constant temperature 63

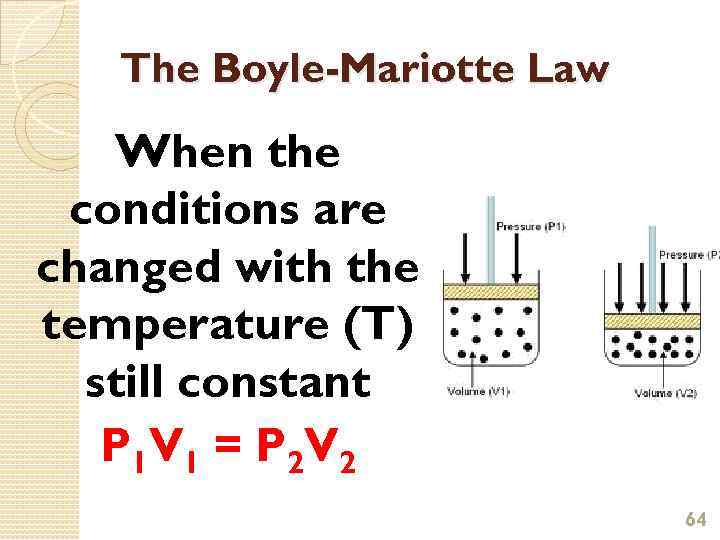
The Boyle-Mariotte Law When the conditions are changed with the temperature (T) still constant P 1 V 1 = P 2 V 2 64

The Boyle-Mariotte Law (Boyle’s Law) Note that the readings of P and V must be taken slowly to maintain constant temperature because when air is compressed, it warms up slightly. 65

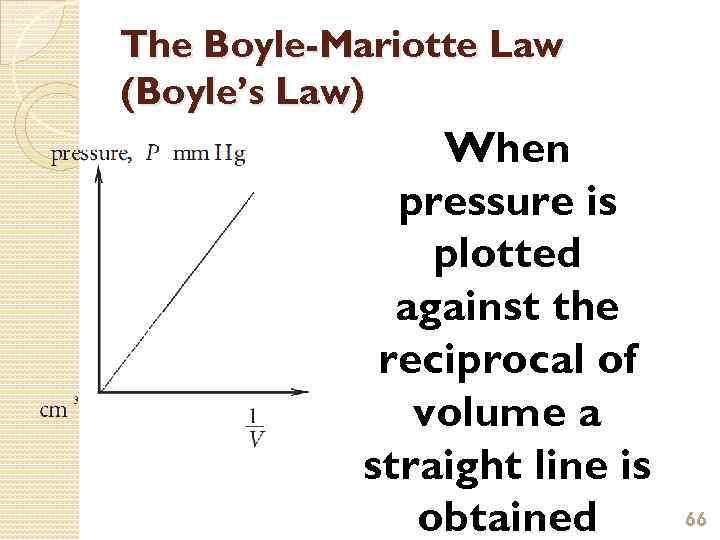
The Boyle-Mariotte Law (Boyle’s Law) When pressure is plotted against the reciprocal of volume a straight line is obtained 66

Objective 9 describe changes in volume due to temperature with constant pressure (Pressure Law or Law of Gay-Lussac in Kazakh books);

Charles (Gay-Lussac) Law As the temperature of a gas is increased, the average kinetic energy per molecule increases. The increase in velocity of the molecules leads to a greater rate of collisions, and each collision involves greater impulse. Hence the volume of the gas increases as the collisions with the sides of the container increase. 68

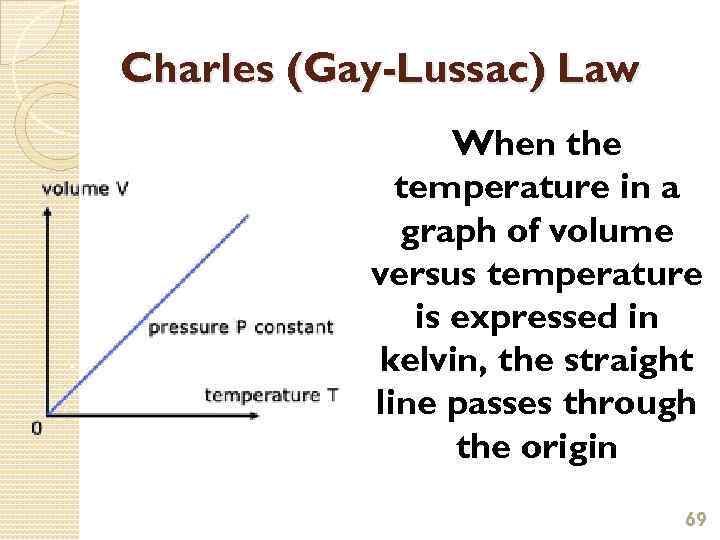
Charles (Gay-Lussac) Law When the temperature in a graph of volume versus temperature is expressed in kelvin, the straight line passes through the origin 69

Go to simulation

Objective 10 plot and analyze graphs of isoprocesses;

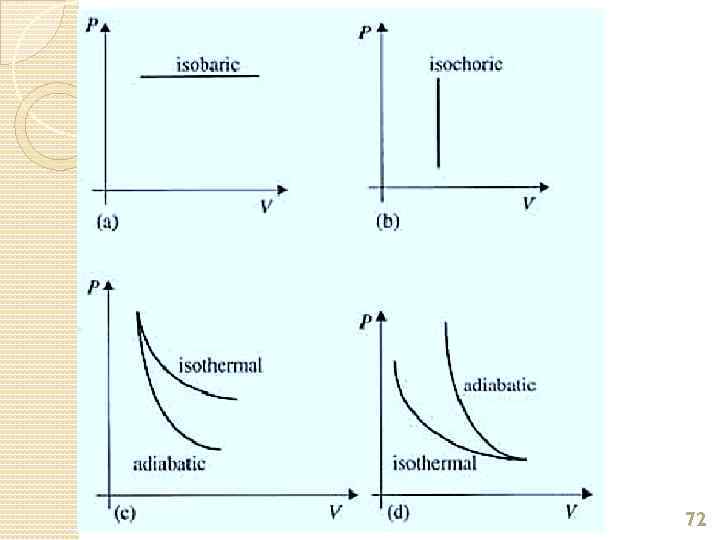
72

Processes on a PV Graph Isobaric Process – process in which the gas expands or contracts at constant pressure. Since P is fixed, work done W = PΔV. 2. Isochoric Process - a process in which the volume of the gas stays fixed. Note that NO WORK is done on or by the gas in this process. 1. 73

Processes on a PV Graph Isothermal Process – process in which the temperature of the system remains constant. 4. Adiabatic Process - a process during which the gas does not absorb or give out any thermal energy, so Q = 0. 3. 74

Gas Transformations For any gas, we can change the state variables: ◦ Changes at constant pressure (isobaric) ◦ Changes at constant volume (isochoric) ◦ Changes at constant temperature (isothermal) Using the ideal gas law, can you sketch an isobaric, isochoric or isothermal graphs?

Thermodynamic Processes The internal energy U of a thermodynamic system is the sum of the KE of all particles. Adding heat increases internal energy! When a gas expands it does work on its surroundings. That work is equal to the area under the P-V curve, or Work = P × ΔV

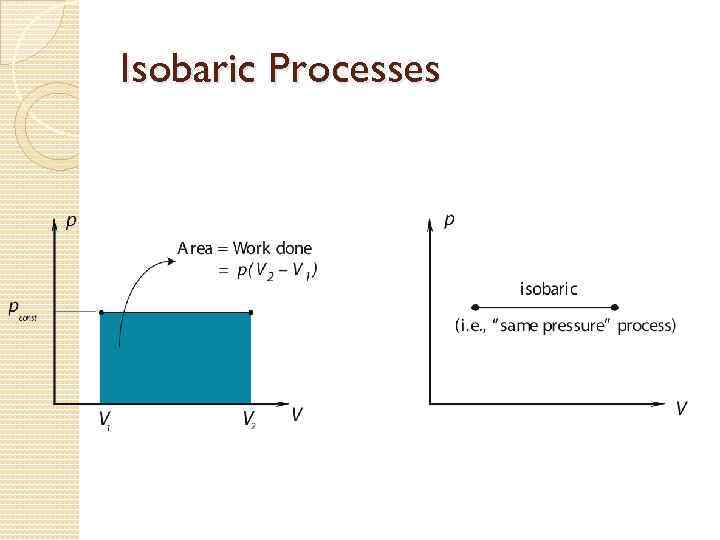
Isobaric Processes

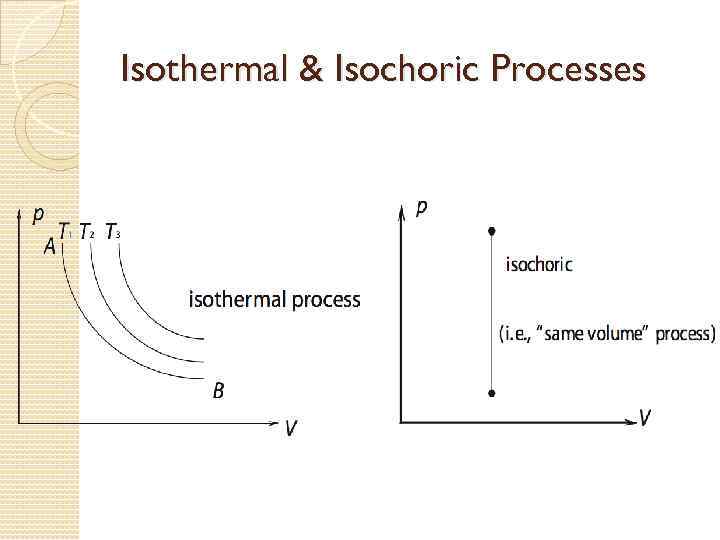
Isothermal & Isochoric Processes

Isochoric W = P ΔV = 0 Therefore W = 0 Q = ΔU

Adiabatic Processes An adiabatic process is when Q = 0 To ensure that no heat enters or leaves the system during an adiabatic process it is important to ◦ make sure that the system is extremely well insulated. ◦ carry out the process rapidly so that the heat does not have the time to leave the system.

Adiabatic Q = W + ΔU O = W + ΔU = -W

Examples If 22 J of work is done on a system and 3. 4 × 102 J of heat is added, determine the change internal energy of the system. (Note: is the work positive or negative? )

Examples 6. 0 dm 3 of an ideal gas is at a pressure of 202. 6 k. Pa. It is heated so that it expands at constant pressure 3. Determine until its volume is 12 dm the work done by the gas.

Examples If 22 J of work is done on a system and 3. 4 × 102 J of heat is added, determine the change internal energy of the system. (Note: is the work positive or negative? )

Examples An ideal gas with volume 0. 05 m 3 is in a cylinder with a moveable piston. 8. 0 x 103 J of heat energy is absorbed by the gas and it expands at constant pressure of 120 k. Pa to a volume of 0. 1 m 3. i. Name the process applied to the gas. ii. How much work was done by the gas? iii. Find the change in the internal energy of the gas.

Week 4

Objective 11 understand apply first law of thermodynamics;

1 st Law of Thermodynamics If the amounts of thermal energy and work are not small, then ΔU = Q – W Q = W + ΔU 89

First Law of Thermodynamics “Conservation of Energy Law” Q = ΔU + W ◦ Q is the heat added (in Joule, J) ◦ ΔU is the change in internal energy (in Joule, J) ◦ W is the work done by the gas (in Joule, J) All variables can be positive or negative. What does a negative sign mean?

1 st Law of Thermodynamics The 1 st Law of thermodynamics is a general statement of energy conservation: the heat Q added to a system minus the net work W done by the system equals the change in the internal energy ΔU of the system. 91

Free expansion Q =0 W = 0 ΔU = 0 V x ΔP= ΔU

Here’s a problem to make you think.

Sample Problem A gas in a container with a piston expands isothermally. If thermal energy Q = 105 J is given to the gas, what is the work done by the gas? 97

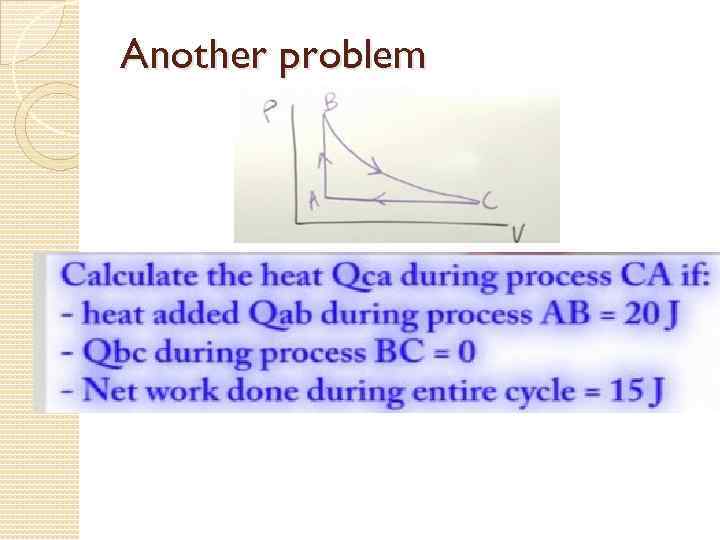
Another problem

Sample Problem 75 joules of work is done to compress a gas, while 20 joules of heat is removed as heat. A. Since the gas is compressed, is the W done on the gas + or −? B. Since heat is removed, is Q + or −? C. Use the First Law of Thermodynamics to find the change of internal energy of the gas.

Sample Problem 35 joules of work is done by a gas as it expands, yet the gas doesn’t change temperature. A. Since the gas is expanded, is W + or −? B. Since the gas doesn’t change temperature, what is the U (change of internal energy) for the gas? C. How much heat (Q) was added?

Objective 12 distinguish graphs of adiabatic and isothermal processes;

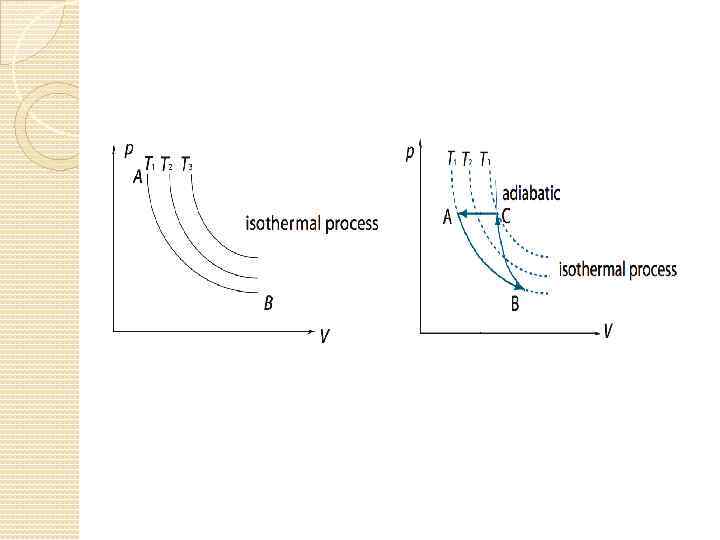
Objective 13 understand second law of thermodynamics;

The 2 nd Law of Thermodynamics Not all thermal energy in a thermal system is available to do work. It is impossible for an engine working in a cycle to transform a given amount of heat from a reservoir completely into work. It is impossible to make a cyclic engine whose only effect is to transfer thermal energy from a colder body to a hotter body.

The 2 nd Law of Thermodynamics The total entropy of any system plus that of its environment increases as a result of all natural processes. The entropy of the Universe increases Natural processes tend to move toward a state of greater disorder.

Which has more entropy? A. A liquid or a gas? B. An object with kinetic energy or after the kinetic energy turns to heat? C. Billiard (pool) balls when the are racked or after they are broken apart (scattered around the table)?

Week 5

Objective 14 understand describe principles of work of heat engines;

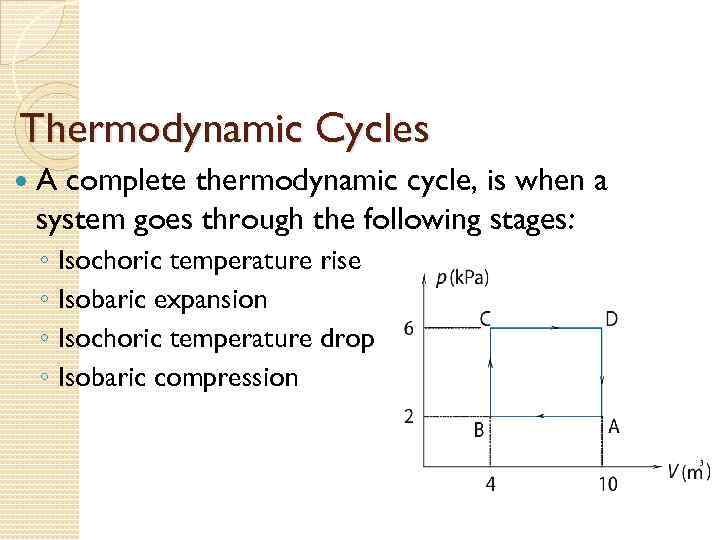
Thermodynamic Cycles A complete thermodynamic cycle, is when a system goes through the following stages: ◦ ◦ Isochoric temperature rise Isobaric expansion Isochoric temperature drop Isobaric compression

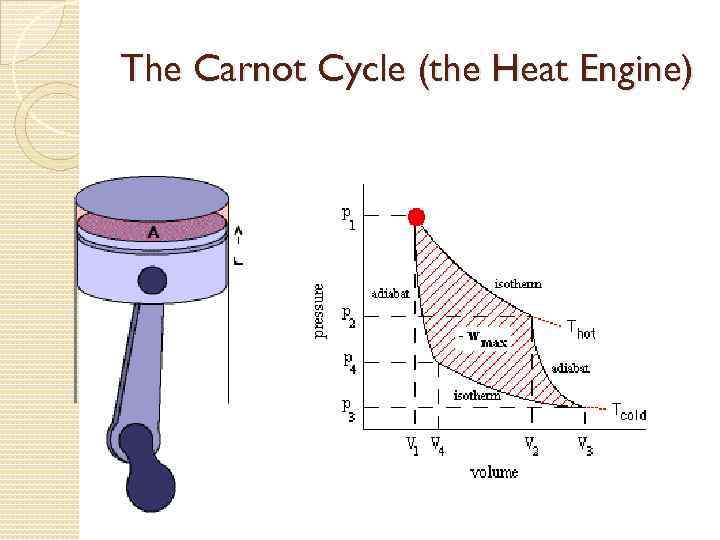
The Carnot Cycle (the Heat Engine)

Reverse Carnot Cycle (Heat Pump) In the previous example, heat was added to the system. In a reverse carnot cycle, heat is extracted from the system (Refrigerator!)

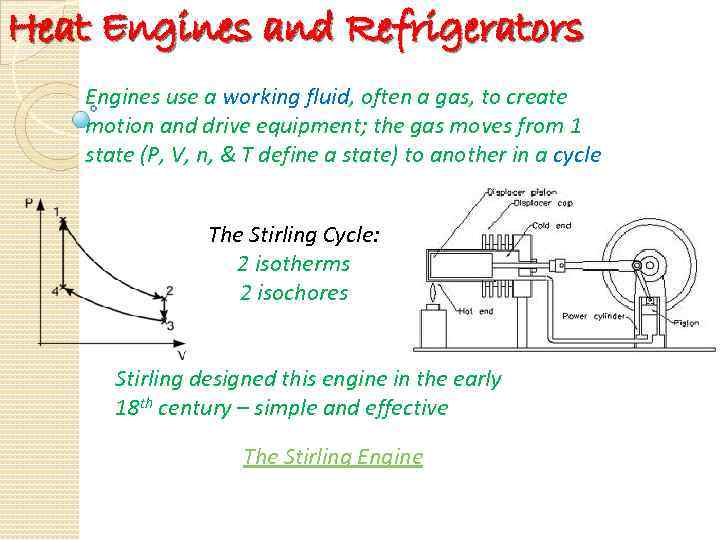
Heat Engines and Refrigerators Engines use a working fluid, often a gas, to create motion and drive equipment; the gas moves from 1 state (P, V, n, & T define a state) to another in a cycle The Stirling Cycle: 2 isotherms 2 isochores Stirling designed this engine in the early 18 th century – simple and effective The Stirling Engine

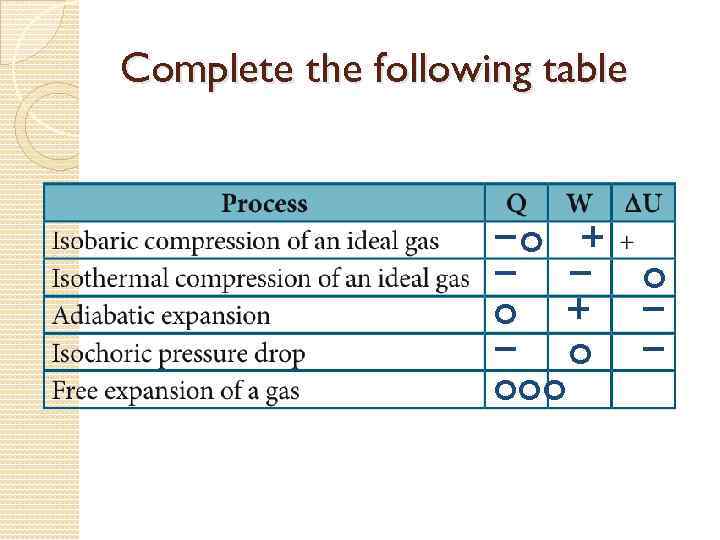
Complete the following table −o + − − o − ooo

Cyclic process After initial interchanges of Q and W the system returns to its initial state. ΔU = 0 Q = W

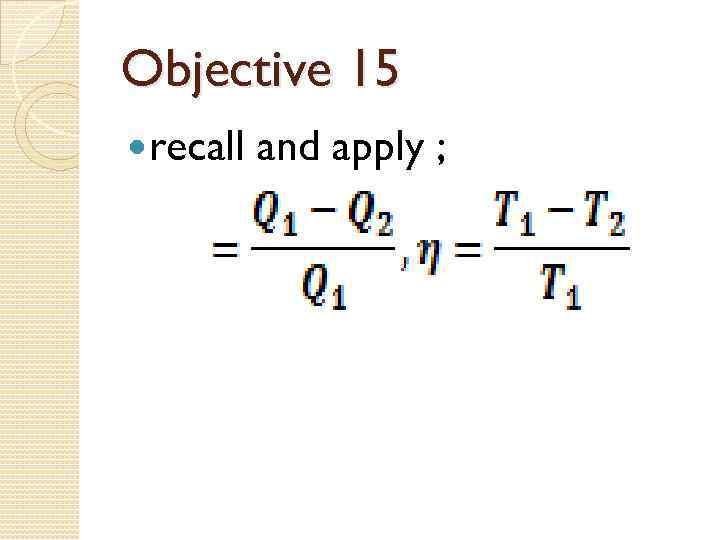
Objective 15 recall and apply ;

Problem: Squeezing a Tank of Gas Pure helium gas is admitted into a tank containing a movable piston. The initial volume, pressure, and temperature of the gas are 15. 0103 m 3, 200 k. Pa, and 300 K, respectively. If the volume is decreased to 12. 0103 m 3 and the pressure increased to 350 k. Pa, find the final temperature of the gas.

Solution Let us model the helium as an ideal gas. If no gas escapes from the tank, the number of moles of gas remains constant; therefore, using PVn. RT at the initial and final conditions gives

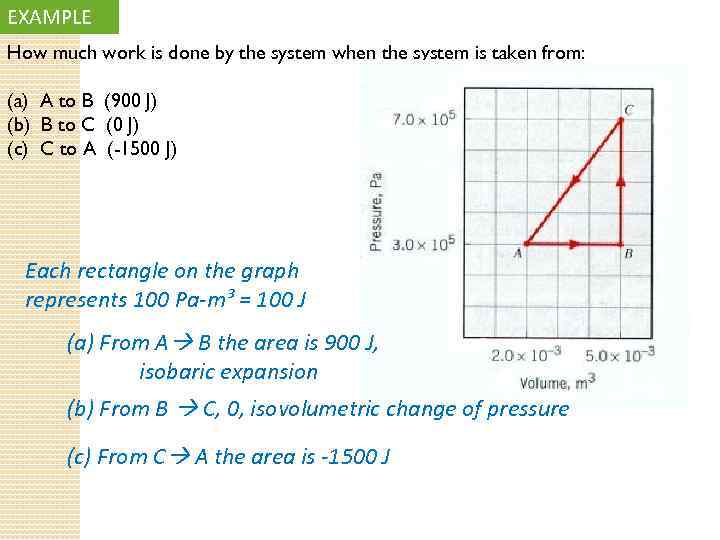
EXAMPLE How much work is done by the system when the system is taken from: (a) A to B (900 J) (b) B to C (0 J) (c) C to A (-1500 J) Each rectangle on the graph represents 100 Pa-m³ = 100 J (a) From A B the area is 900 J, isobaric expansion (b) From B C, 0, isovolumetric change of pressure (c) From C A the area is -1500 J

EXAMPLE 10 grams of steam at 100 C at constant pressure rises to 110 C: P = 4 x 105 Pa T = 10 C V = 30. 0 x 10 -6 m 3 c = 2. 01 J/g What is the change in internal energy? U = Q – W U = mc T – P V U = 189 J So heating the steam produces a higher internal energy and expansion

EXAMPLE Aluminum cube of side L is heated in a chamber at atmospheric pressure. What is the change in the cube's internal energy if L = 10 cm and T = 5 °C? U = Q – W Q = mc T m = V 0 = L 3 W = P V V = V 0 T U = mc T – P V U = V 0 c T – P V 0 T U = V 0 T ( c – P ) U = L³ T ( c – P ) c. Al = 0. 90 J/g°C Al = 72(10 -6) °C-1 Patm = 101. 5 k. Pa Al = 2. 7 g/cm³ U = 0. 10³(5)((2700)(900) – 101. 5(10³)(72(10 -6)) U = 12, 150 J NB: P is neglible

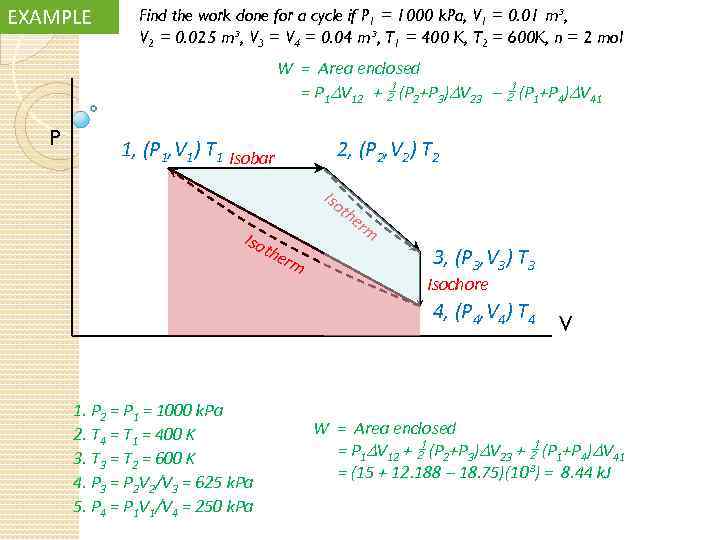
EXAMPLE Find the work done for a cycle if P 1 = 1000 k. Pa, V 1 = 0. 01 m³, V 2 = 0. 025 m³, V 3 = V 4 = 0. 04 m³, T 1 = 400 K, T 2 = 600 K, n = 2 mol W = Area enclosed = P 1 V 12 + (P 2+P 3) V 23 – (P 1+P 4) V 41 P 1, (P 1, V 1) T 1 Isobar 2, (P 2, V 2) T 2 Iso the rm er m 3, (P 3, V 3) T 3 Isochore 4, (P 4, V 4) T 4 1. P 2 = P 1 = 1000 k. Pa 2. T 4 = T 1 = 400 K 3. T 3 = T 2 = 600 K 4. P 3 = P 2 V 2/V 3 = 625 k. Pa 5. P 4 = P 1 V 1/V 4 = 250 k. Pa V W = Area enclosed = P 1 V 12 + (P 2+P 3) V 23 + (P 1+P 4) V 41 = (15 + 12. 188 – 18. 75)(10³) = 8. 44 k. J

EXAMPLE P Find the internal energy for each state if P 1 = 1000 k. Pa, V 1 = 0. 01 m³, V 2 = 0. 025 m³, V 3 = V 4 = 0. 04 m³, T 1 = 400 K, T 2 = 600 K, n = 2 mol 1, (P 1, V 1) T 1 Isobar 2, (P 2, V 2) T 2 Iso 1. P 2 = P 1 = 1000 k. Pa 2. T 4 = T 1 = 400 K 3. T 3 = T 2 = 600 K 4. P 3 = P 2 V 2/V 3 = 625 k. Pa 5. P 4 = P 1 V 1/V 4 = 250 k. Pa th Iso the rm er m 3, (P 3, V 3) T 3 Isochore 4, (P 4, V 4) T 4 6. U 1 = n. RT 1 = 9972 J 7. U 4 = U 1 = 9972 J 8. U 2 = n. RT 2 = 14958 J 9. U 3 = U 2 = 14958 J V

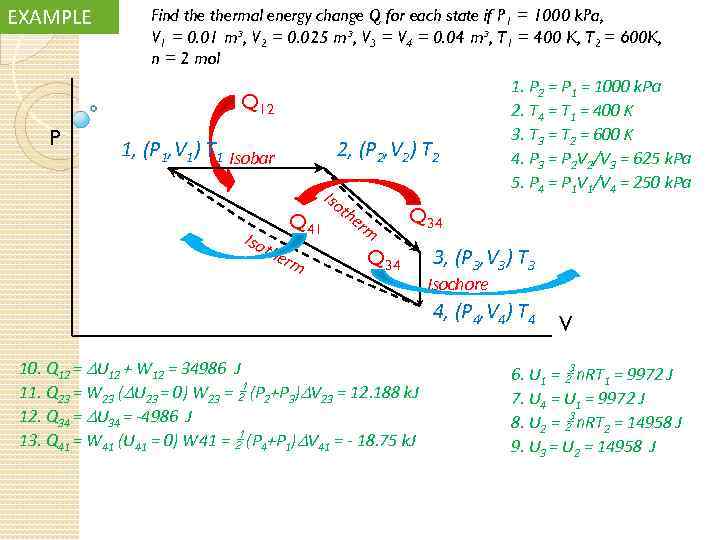
EXAMPLE Find thermal energy change Q for each state if P 1 = 1000 k. Pa, V 1 = 0. 01 m³, V 2 = 0. 025 m³, V 3 = V 4 = 0. 04 m³, T 1 = 400 K, T 2 = 600 K, n = 2 mol Q 12 P 1, (P 1, V 1) T 1 Isobar Iso 2, (P 2, V 2) T 2 the Q 41 rm Iso th er m 1. P 2 = P 1 = 1000 k. Pa 2. T 4 = T 1 = 400 K 3. T 3 = T 2 = 600 K 4. P 3 = P 2 V 2/V 3 = 625 k. Pa 5. P 4 = P 1 V 1/V 4 = 250 k. Pa Q 34 3, (P 3, V 3) T 3 Isochore 4, (P 4, V 4) T 4 10. Q 12 = U 12 + W 12 = 34986 J 11. Q 23 = W 23 ( U 23 = 0) W 23 = (P 2+P 3) V 23 = 12. 188 k. J 12. Q 34 = U 34 = -4986 J 13. Q 41 = W 41 (U 41 = 0) W 41 = (P 4+P 1) V 41 = - 18. 75 k. J V 6. U 1 = n. RT 1 = 9972 J 7. U 4 = U 1 = 9972 J 8. U 2 = n. RT 2 = 14958 J 9. U 3 = U 2 = 14958 J

Sample Problem A gas is compressed slowly by a piston. Explain why the temperature of the gas will stay the same. 2. A gas is compressed rapidly by a piston. Explain why the temperature of the gas will increase. 1. 1 27

Sample Problem A gas expands isothermally. Explain from a molecular point view why pressure decreases. 4. A gas is heated at constant pressure. Explain why the volume must increase as well. 3. 1 28

Sample Problem How many molecules are there in 6 g of hydrogen gas? 2. Make a rough estimate of the number of water molecules in an ordinary glass of water containing 0. 3 L with a mass of about 1. 1 29

Sample Problems 1. The pressure of a gas is 2 atm and its volume is 0. 9 L. If the pressure is increased to 6 atm at constant temperature, what is the new volume? 1 30

Sample Problems 2. A gas expands at constant pressure from an original volume of 2 L at 22°C to a volume of 4 L. What is the new temperature? 1 31

Sample Problems 3. A gas in a container of fixed volume is heated from a temperature of 20°C and pressure of 3 atm to a temperature of 85°C. What is the new pressure? 1 32

Sample Problems 1. How many moles of gas are there in a gas of temperature 300 K, volume 0. 02 m 3 and 5 Pa? pressure 2 × 10 1 33

Sample Problems 2. A container of hydrogen 3 and of volume 0. 1 m temperature 25°C contains 3. 20 × 1023 molecules. What is the pressure in the container? 1 34

Sample Problems 3. A gas of volume 2 L, pressure 3 atm and temperature 300 K expands to a volume of 3 L and a pressure of 4 atm. What is the new temperature of the gas? 1 35

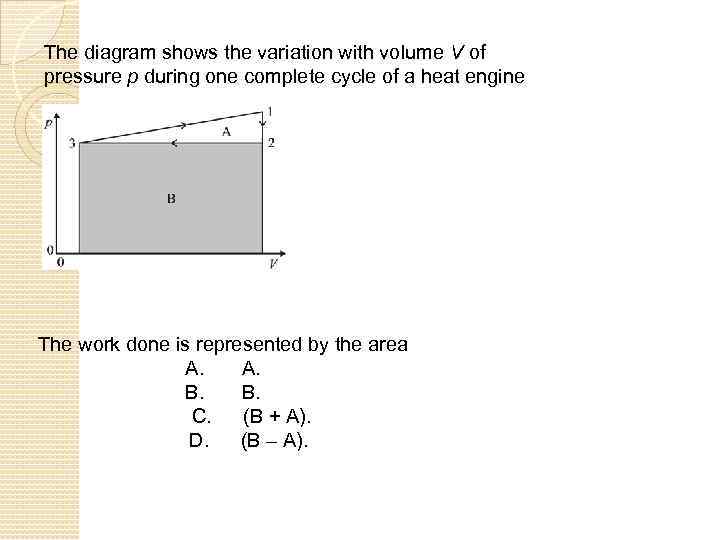
The diagram shows the variation with volume V of pressure p during one complete cycle of a heat engine The work done is represented by the area A. A. B. B. C. (B + A). D. (B – A).

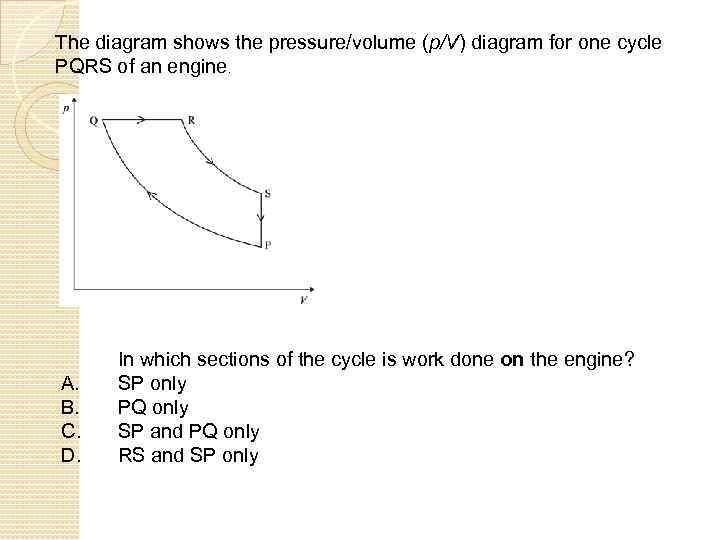
The diagram shows the pressure/volume (p/V) diagram for one cycle PQRS of an engine. A. B. C. D. In which sections of the cycle is work done on the engine? SP only PQ only SP and PQ only RS and SP only

A beaker contains water at a higher temperature than its surroundings. Which of the following correctly describes the entropy change in the water and in the surroundings as the water cools? entropy of the water entropy of the surroundings A. decreases B. decreases increases C. increases decreases D. increases Boiling water in a beaker is heated continuously. Steam escapes into the surroundings. Which of the following correctly lists the entropy changes of the boiling water and the surroundings? boiling water surroundings A. increases constant B. increases C. decreases constant D. decreases increases

Eg shaking a jar with layers of salt and pepper natural process is from a state of relative order (layers) to one of disorder (mixture), the reverse is not possible. Eg breaking coffee cup. Eg mixing hot and cold water Eg “Heat death” of universe Eg Entropy as “time’s arrow”, can tell us which way time is going (eg a film running backwards)

For example… A monatomic gas is kept at constant pressure of 3. 00 x 105 Pa, initial volume 0. 100 m 3 and 300 K. If the gas is compressed at constant pressure, down to 0. 080 m 3, find a) The work done on the gas b) The heat taken out of the gas