ef65ad9c2d8f6b5861f63df168cb0034.ppt
- Количество слайдов: 104

THEORY OF FIRM BEHAVIOR COSTS OF THE FIRM

Firm’s Choice: Firm’s Costs and Production Decision n A firm chooses: q q n What quantity of the good to produce, The price of the good (sometimes. . . ). Firm’s decision depends on: q q Costs of production. The degree of competition in the market (if there are more sellers, more competitive).

Firm’s Choice: Firm’s Costs and Production Decision n Firm’s Objective q The goal of a firm is to maximize profits.

Total Revenue, Total Cost, and Profit n Profit is the firm’s total revenue minus its total cost. Profit = Total Revenue - Total Cost

Total Revenue, Total Cost, and Profit n Total Revenue q n The amount a firm receives for the sale of its output. For a competitive firm, TR = P x Q Total Cost q The market value of the inputs a firm uses in production.

Economic Profit versus Accounting Profit n n Economic profit is not the same as accounting profit. When calculating economic profit, we include all opportunity costs including hidden (implicit) costs. Accounting profit (as it appears on balance sheets) refers to the firm’s total revenue minus only the firm’s open (explicit) costs.

Costs as Opportunity Costs n Example: Costs of Your Textile Factory q q Worker’s wages, electricity, cost of machines, rent are open (explicit) costs. Instead of starting the textile factory, you could work as an engineer for 2, 500 liras per month. Then the hidden (implicit) cost of running the textile factory is 2, 500 liras per month.

Economic Profit versus Accounting Profit n n A firm earns positive economic profit only if total revenue exceeds both open and hidden opportunity costs. Economic profit is always less than or equal to accounting profit: A firm could be making positive accounting profit but at the same time zero or negative economic profit.

Production • An entrepreneur must put together resources -- land, labour, capital -- and produce a product people will be willing and able to purchase

Production Economics • Managers must decide not only what to produce for the market, but also how to produce it in the most efficient or least cost manner. • Economics offers widely accepted tools for judging whether the production choices are least cost. • A production function relates the most that can be produced from a given set of inputs. » Production functions allow measures of the marginal product of each input. Slide 10

PRODUCTION FUNCTION • THE RELATIONSHIP BETWEEN THE AMOUNT OF INPUT REQUIRED AND THE AMOUNT OF OUTPUT THAT CAN BE OBTAINED IS CALLED THE PRODUCTION FUNCTION

PRODUCTION AND COSTS n The Production Function q The production function shows the relationship between quantity of inputs (Ex: number of workers) used to make a good and the quantity of output of that good.
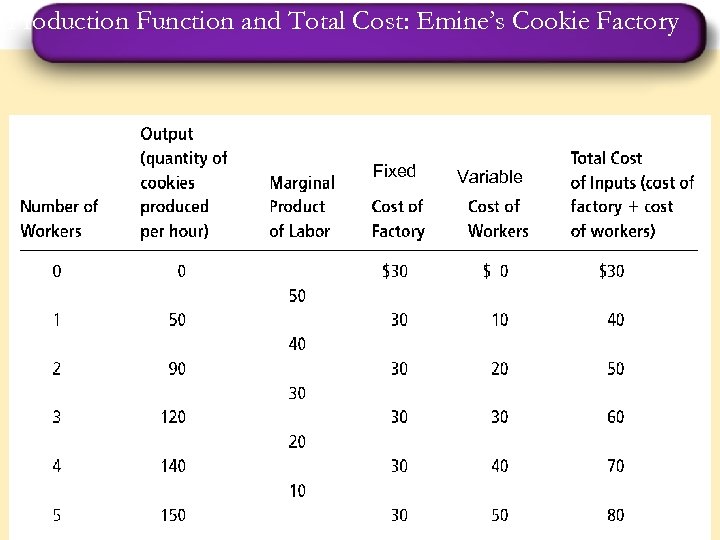
Production Function and Total Cost: Emine’s Cookie Factory Fixed 1 Variable 13
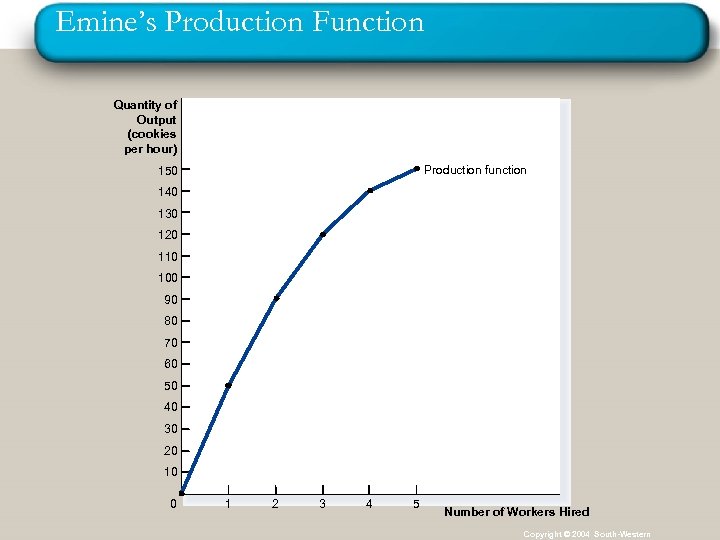
Emine’s Production Function Quantity of Output (cookies per hour) Production function 150 140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 Number of Workers Hired Copyright © 2004 South-Western

The Production Function n Marginal Product q The marginal product of labor (any input) is the change in output produced by an additional worker (additional input).

The Production Function n Diminishing Marginal Product q Diminishing marginal product: Keeping all other inputs fixed, marginal product of one of the inputs declines as the quantity of that input increases. n n Ex: As more and more workers are hired at a firm, each additional worker contributes less and less to output because the firm has a fixed amount of machines & equipment & capacity. Another example: a farm with fixed area, machines, technology, labor. Try planting 100 gr. seeds or 200 gr. or 300 gr. seeds.

The Production Function n Diminishing Marginal Product q q The slope of the production function measures the marginal product of labor. When the marginal product of labor declines, the production function becomes flatter.
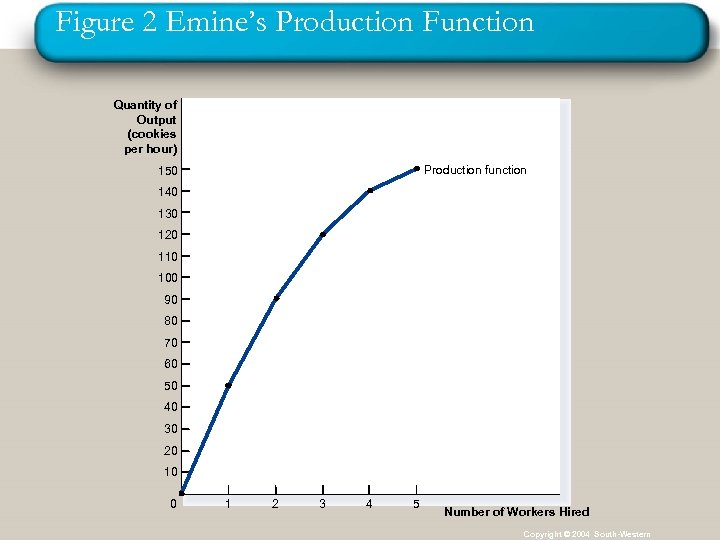
Figure 2 Emine’s Production Function Quantity of Output (cookies per hour) Production function 150 140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 Number of Workers Hired Copyright © 2004 South-Western
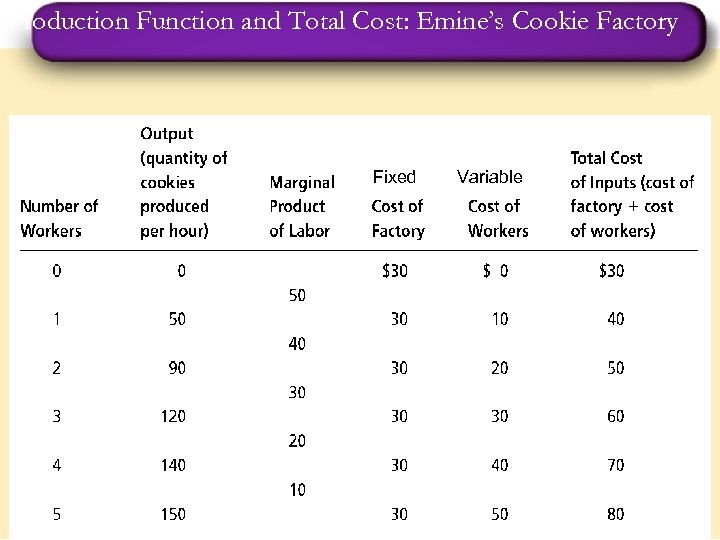
Production Function and Total Cost: Emine’s Cookie Factory Fixed Variable

What can you say about Marginal Product ? • As the quantity of a variable input (labour, in the example) increases while all other inputs are fixed, output rises. Initially, output will rise more and more rapidly, but eventually it will slow down and perhaps even decline. • This is called the LAW OF DIMINISHING MARGINAL RETURNS

LAW OF DIMINISHING RETURNS IT HOLDS THAT WE WILL GET LESS & LESS EXTRA OUTPUT WHEN WE ADDITIONAL DOSES OF AN INPUT WHILE HOLDING OTHER INPUTS FIXED. IT IS ALSO KNOWN AS LAW OF VARIABLE PROPORTIONS.
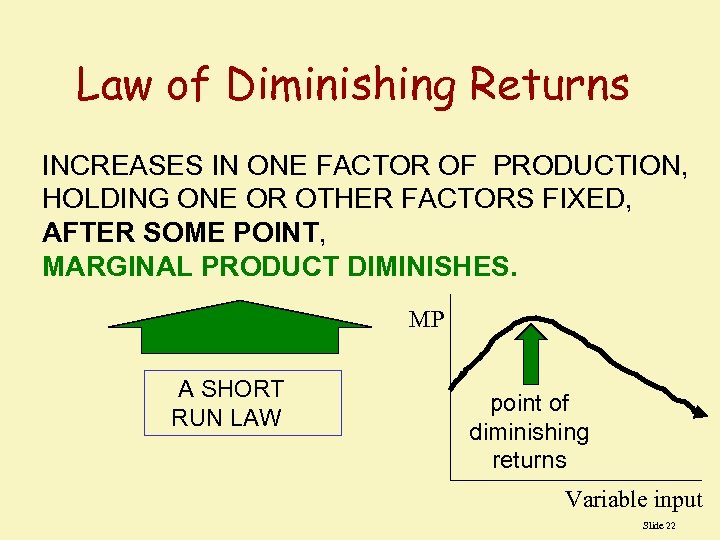
Law of Diminishing Returns INCREASES IN ONE FACTOR OF PRODUCTION, HOLDING ONE OR OTHER FACTORS FIXED, AFTER SOME POINT, MARGINAL PRODUCT DIMINISHES. MP A SHORT RUN LAW point of diminishing returns Variable input Slide 22
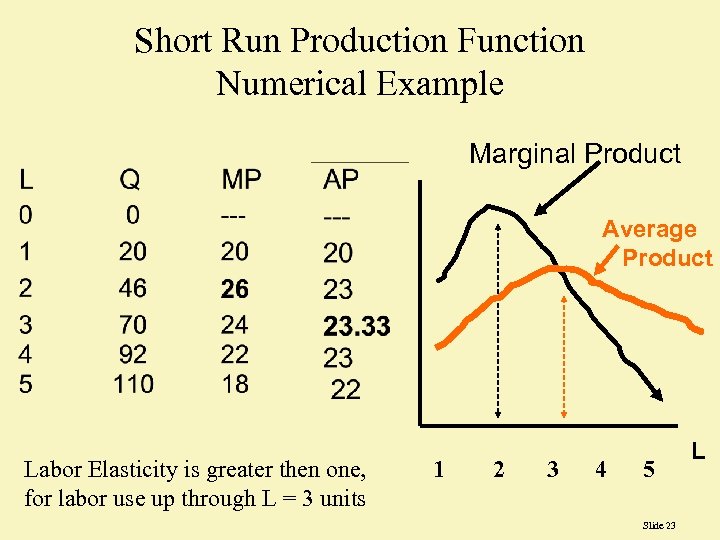
Short Run Production Function Numerical Example Marginal Product Average Product Labor Elasticity is greater then one, for labor use up through L = 3 units 1 2 3 4 5 Slide 23 L

• When MP > AP, then AP is RISING » IF YOUR MARGINAL GRADE IN THIS CLASS IS HIGHER THAN YOUR GRADE POINT AVERAGE, THEN YOUR G. P. A. IS RISING • When MP < AP, then AP is FALLING » IF YOUR MARGINAL BATTING AVERAGE IS LESS THAN THAT OF THE NEW YORK YANKEES, YOUR ADDITION TO THE TEAM WOULD LOWER THE YANKEE’S TEAM BATTING AVERAGE • When MP = AP, then AP is at its MAX » IF THE NEW HIRE IS JUST AS EFFICIENT AS THE AVERAGE EMPLOYEE, THEN AVERAGE PRODUCTIVITY DOESN’T CHANGE Slide 24
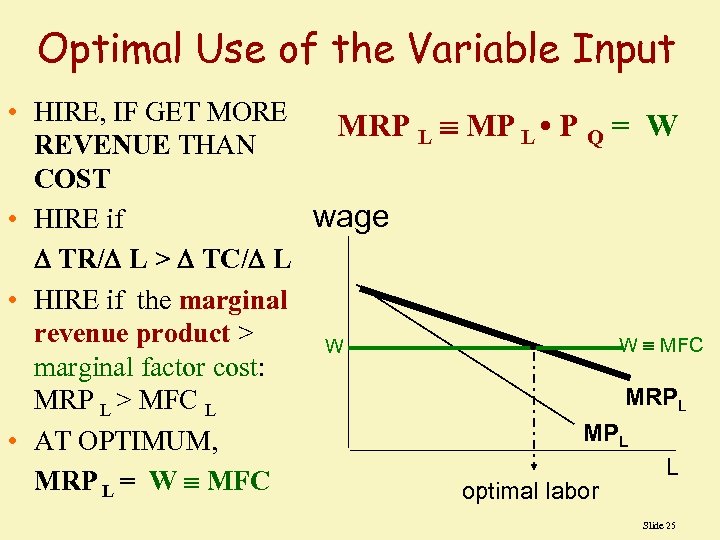
Optimal Use of the Variable Input • HIRE, IF GET MORE MRP L MP L • P Q = W REVENUE THAN COST wage • HIRE if TR/ L > TC/ L • HIRE if the marginal revenue product > W MFC W • marginal factor cost: MRPL MRP L > MFC L MPL • AT OPTIMUM, L MRP L = W MFC optimal labor Slide 25

MRP L is the Demand for Labor • If Labor is MORE productive, demand for labor increases • If Labor is LESS productive, demand for labor decreases • Suppose an EARTHQUAKE destroys capital • MP L declines with less capital, wages and labor are HURT SL W DL D’ L L’ L Slide 26

COMBINING RESOURCES • THERE ARE MANY COMBINATIONS OF RESOURCES THAT COULD BE USED • CONSIDER THE FOLLOWING TABLE SHOWING DIFFERENT NUMBER OF MECHANICS AND AMOUNT OF CAPITAL THAT THE HYPOTHETICAL FIRM, INDIA INC. , MIGHT USE
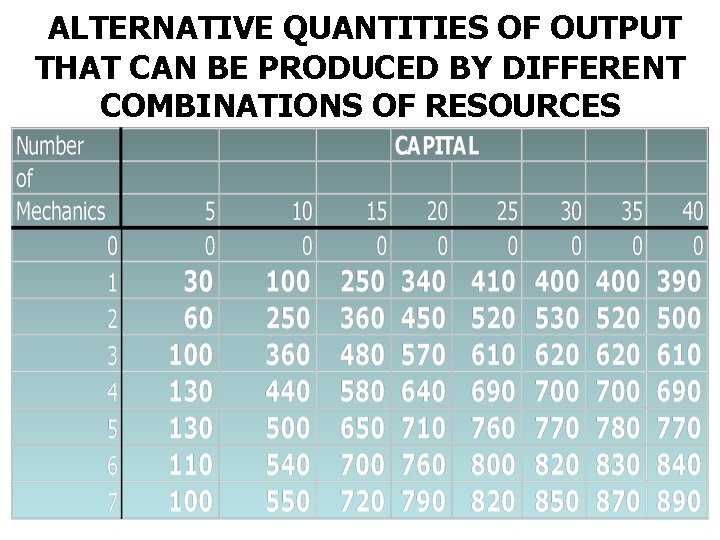
ALTERNATIVE QUANTITIES OF OUTPUT THAT CAN BE PRODUCED BY DIFFERENT COMBINATIONS OF RESOURCES

PRODUCTION IN THE SHORT RUN • THE SHORT RUN IS A PERIOD JUST SHORT ENOUGH THAT AT LEAST ONE RESOURCE (INPUT-INDUSTRIAL PLANT, MACHINES) CANNOT BE CHANGED -- IS FIXED OR INELASTIC. THUS IN THE SHORT RUN PROUDCTION OF A COMMODITY CAN BE INCREASED BY INCREASING THE USE OF ONLY VARIABLE INPUTS LIKE LABOUR AND RAW MATERIALS.
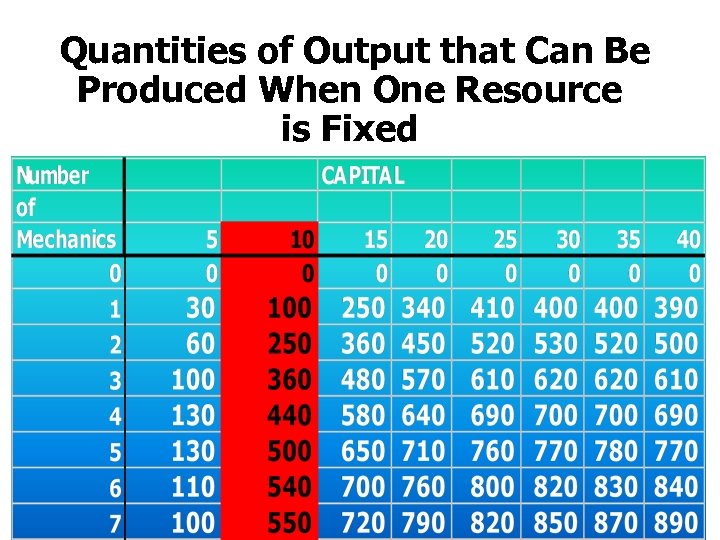
Quantities of Output that Can Be Produced When One Resource is Fixed

LONG RUN • THE LONG RUN IS A PERIOD SUFFIECIENTLY LONG THAT ALL FACTORS INCLUDING CAPITAL CAN BE ADJUSTED OR ARE VARIABLE. • THIS MEANS THAT THE FIRM CAN CHOOSE ANY COMBINATION ON THE MANUFACTURING TABLE -- NOT JUST THOSE ALONG COLUMN LABELLED “ 10”
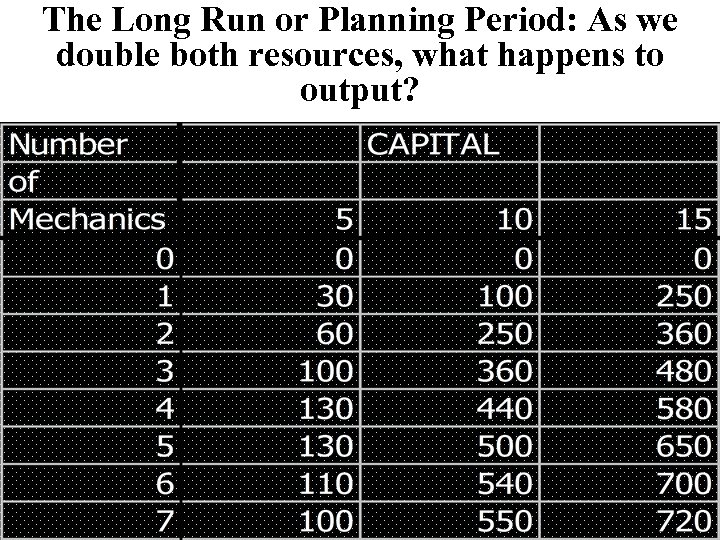
The Long Run or Planning Period: As we double both resources, what happens to output?
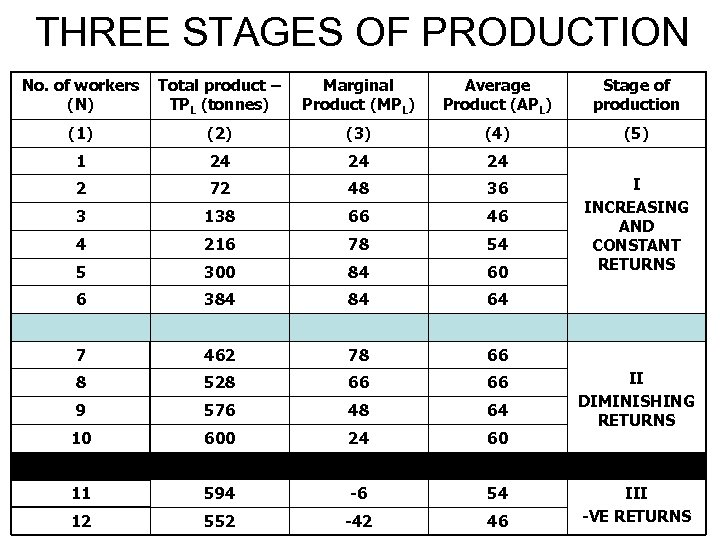
THREE STAGES OF PRODUCTION No. of workers (N) Total product – TPL (tonnes) Marginal Product (MPL) Average Product (APL) Stage of production (1) (2) (3) (4) (5) 1 24 24 24 2 72 48 36 3 138 66 46 4 216 78 54 5 300 84 60 6 384 84 64 7 462 78 66 8 528 66 66 9 576 48 64 10 600 24 60 11 594 -6 54 12 552 -42 46 I INCREASING AND CONSTANT RETURNS II DIMINISHING RETURNS III -VE RETURNS
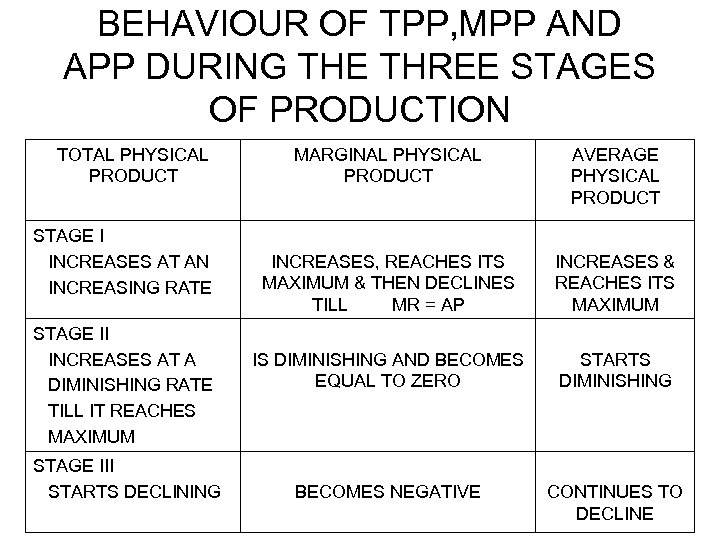
BEHAVIOUR OF TPP, MPP AND APP DURING THE THREE STAGES OF PRODUCTION TOTAL PHYSICAL PRODUCT STAGE I INCREASES AT AN INCREASING RATE STAGE II INCREASES AT A DIMINISHING RATE TILL IT REACHES MAXIMUM STAGE III STARTS DECLINING MARGINAL PHYSICAL PRODUCT AVERAGE PHYSICAL PRODUCT INCREASES, REACHES ITS MAXIMUM & THEN DECLINES TILL MR = AP INCREASES & REACHES ITS MAXIMUM IS DIMINISHING AND BECOMES EQUAL TO ZERO STARTS DIMINISHING BECOMES NEGATIVE CONTINUES TO DECLINE

FROM THE ABOVE TABLE ONLY STAGE II IS RATIONAL WHICH MEANS RELEVANT RANGE FOR A RATIONAL FIRM TO OPERATE. IN STAGE I IT IS PROFITABLE FOR THE FIRM TO KEEP ON INCREASING THE USE OF LABOUR. IN STAGE III, MP IS NEGATIVE AND HENCE IT IS INADVISABLE TO USE ADDITIONAL LABOUR. i. e ONLY STAGE I AND III ARE IRRATIONAL
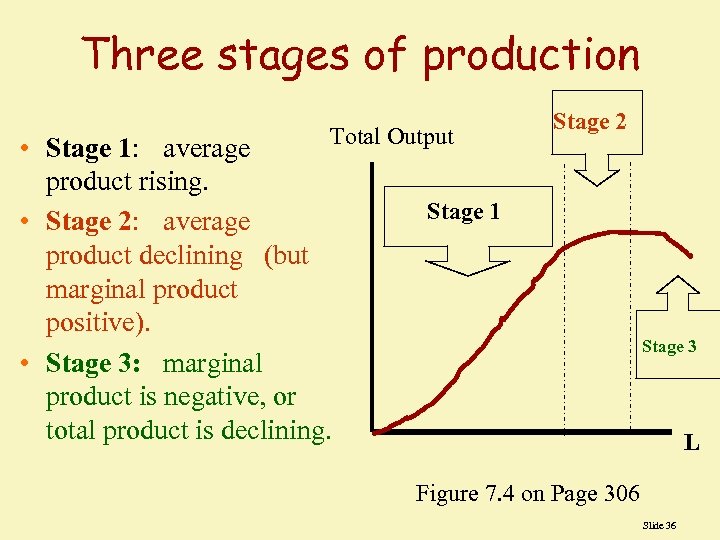
Three stages of production Total Output • Stage 1: average product rising. Stage 1 • Stage 2: average product declining (but marginal product positive). • Stage 3: marginal product is negative, or total product is declining. Stage 2 Stage 3 L Figure 7. 4 on Page 306 Slide 36

The Production Function • A Production Function is the maximum quantity from any amounts of inputs • If L is labor and K is capital, one popular functional form is known as the Cobb. Douglas Production Function • Q = • K 1 • L 2 is a Cobb-Douglas Production Function • The number of inputs is often large. But economists simplify by suggesting some, like materials or labor, is variable, whereas plant and equipment is fairly fixed in the short run.
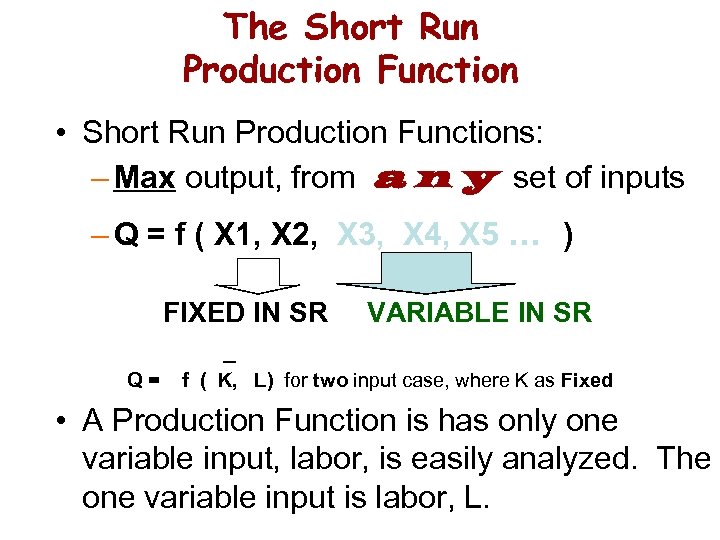
The Short Run Production Function • Short Run Production Functions: – Max output, from a n y set of inputs – Q = f ( X 1, X 2, X 3, X 4, X 5. . . ) FIXED IN SR VARIABLE IN SR _ Q= f ( K, L) for two input case, where K as Fixed • A Production Function is has only one variable input, labor, is easily analyzed. The one variable input is labor, L.

Returns to Scale A function is homogeneous of degree-n Constant Returns to Scale is homogeneous of degree 1. if multiplying all inputs by (lambda) increases the dependent variable by n Q = f ( K, L) So, f( K, L) = n • Q 10% more all inputs leads to 10% more output. Cobb-Douglas Production Functions are homogeneous of degree +

Cobb-Douglas Production Functions Q = A • K • L is a Cobb-Douglas Production Function IMPLIES: Can be CRS, DRS, or IRS if + 1, then constant returns to scale if + < 1, then decreasing returns to scale if + > 1, then increasing returns to scale Coefficients are elasticities is the capital elasticity of output, often about. 67 is the labor elasticity of output, often about. 33 which are EK and E L Most firms have some slight increasing returns to scale

Problem Suppose: 1. 2. 3. 4. 5. Q = 1. 4 L. 70 K. 35 Is this function homogeneous? Is the production function constant returns to scale? What is the production elasticity of labor? What is the production elasticity of capital? What happens to Q, if L increases 3% and capital is cut 10%?

Answers 4. Yes. Increasing all inputs by , increases output by 1. 05. It is homogeneous of degree 1. 05. No, it is not constant returns to scale. It is increasing Returns to Scale, since 1. 05 > 1. . 70 is the production elasticity of labor. 35 is the production elasticity of capital 5. % Q = EL • % L+ EK • % K = 1. 2. 3. . 35(-10%) = 2. 1% -3. 5% = . 7(+3%) + -1. 4%

• Average Product = Q / L – output per labor • Marginal Product = Q / L = d. Q / d. L – output attributable to last unit of labor applied • Similar to profit functions, the Peak of MP occurs before the Peak of average product • When MP = AP, we’re at the peak of the AP curve

Elasticities of Production • The production elasticity of labor, – EL = MPL / APL = ( Q/ L) / (Q/L) = ( Q/ L)·(L/Q) – The production elasticity of capital has the identical in form, except K appears in place of L. • When MPL > APL, then the labor elasticity, EL > 1. – A 1 percent increase in labor will increase output by more than 1 percent. • When MPL < APL, then the labor elasticity, EL < 1. – A 1 percent increase in labor will increase output by less than 1 percent.

ISOQUANT AN ISOQUANT OR ISO PRODUCT CURVE OR EQUAL PRODUCT CURVE OR A PRODUCTION INDIFFERENCE CURVE SHOW THE VARIOUS COMBINATIONS OF TWO VARIABLE INPUTS RESULTING IN THE SAME LEVEL OF OUTPUT. IT IS DEFINED AS A CURVE PASSING THROUGH THE PLOTTED POINTS REPRESENTING ALL THE COMBINATIONS OF THE TWO FACTORS OF PRODUCTION WHICH WILL PRODUCE A GIVEN OUTPUT.
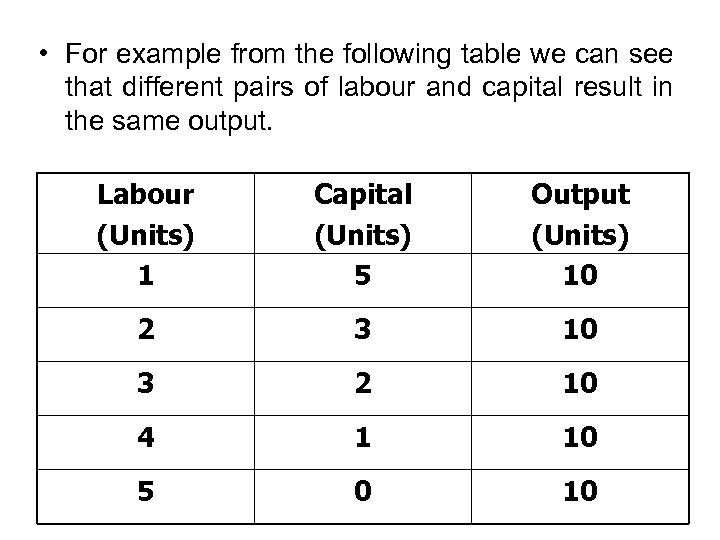
• For example from the following table we can see that different pairs of labour and capital result in the same output. Labour (Units) 1 Capital (Units) 5 Output (Units) 10 2 3 10 3 2 10 4 1 10 5 0 10

FOR EACH LEVEL OF OUTPUT THERE WILL BE A DIFFERENT ISOQUANT. WHEN THE WHOLE ARRAY OF ISOQUANTS ARE REPRESENTED ON A GRAPH, IT IS CALLED AN ISOQUANT MAP. IMPORTANT ASSUMPTIONS THE TWO INPUTS CAN BE SUBSTITUTED FOR EACH OTHER. FOR EXAMPLE IF LABOUR IS REDUCED IN A COMPANY IT WOULD HAVE TO BE COMPENSATED BY ADDITIONAL MACHINERY TO GET THE SAME OUTPUT.

SLOPE OF ISOQUANT THE SLOPE OF AN ISOQUANT HAS A TECHNICAL NAME CALLED THE MARGINAL RATE OF TECHNICAL SUBSTITUTION (MRTS) OR THE MARGINAL RATE OF SUBSTITUTION IN PRODUCTION. THUS IN TERMS OF CAPITAL SERVICES K AND LABOUR L MRTS = Dk/DL

TYPES OF ISOQUANTS 1. LINEAR ISOQUANT 2. RIGHT-ANGLE ISOQUANT 3. CONVEX ISOQUANT

LINEAR ISOQUANT IN LINEAR ISOQUANTS THERE IS PERFECT SUBSTIUTABILTY OF INPUTS. FOR EXAMPLE IN A POWER PLANT EQUIPED TO BURN OIL OR GAS. VARIOUS AMOUNTS OF ELECTRICITY COULD BE PRODUCED BY BURNING GAS, OIL OR A COMBINATION. i. e OIL AND GAS ARE PERFECT SUBSITUTES. HENCE THE ISOQUANT WOULD BE A STRAIGHT LINE.

RIGHT-ANGLE ISOQUANT IN RIGHT-ANGLE ISOQUANTS THERE IS COMPLETE NON-SUBSTIUTABILTY BETWEEN INPUTS. FOR EXAMPLE TWO WHEELS AND A FRAME ARE REQUIRED TO PRODUCE A BYCYCLE THESE CANNOT BE INTERCHANGED. THIS IS ALSO KNOWN AS LEONTIEF ISOQUANT OR INPUT-OUTPUT ISOQUANT.

CONVEX ISOQUANT IN CONVEX ISOQUANTS THERE IS SUBSTIUTABILTY BETWEEN INPUTS BUT IT IS NOT PERFECT. FOR EXAMPLE (1) A SHIRT CAN BE MADE WITH LARGE AMOUNT OF LABOUR AND A SMALL AMOUNT MACHINERY. (2) THE SAME SHIRT CAN BE WITH LESS LABOURERS, BY INCREASING MACHINERY. (3) THE SAME SHIRT BE CAN MADE WITH STILL LESS LABOURERS BUT WITH A LARGER INCREASE MACHINERY. IN

WHILE A RELATIVELY SMALL ADDITION OF MACHINERY FROM M 1(MANUAL EMBROIDERY) TO M 2(TAILORING MACHINE EMBROIDERY) ALLOWS THE INPUT OF LABOURERS TO BE REDUCED FROM L 1 TO L 2. A VERY LARGE INCREASE IN MACHINERY TO M 3 (COMPUTERISED EMBROIDERY) IS REQUIRED TO FURTHER DECREASE LABOUR FROM L 2 TO L 3. THUS SUBSTIUTABILITY OF LABOURERS FOR MACHINERY DIMINISHES FROM M 1 TO M 2 TO M 3.

PROPERTIES OF ISOQUANTS 1. AN ISOQUANT IS DOWNWARD SLOPING TO THE RIGHT. i. e NEGATIVELY INCLINED. THIS IMPLIES THAT FOR THE SAME LEVEL OF OUTPUT, THE QUANTITY OF ONE VARIABLE WILL HAVE TO BE REDUCED IN ORDER TO INCREASE THE QUANTITY OF OTHER VARIABLE.

PROPERTIES OF ISOQUANTS 2. A HIGHER ISOQUANT REPRESENTS LARGER OUTPUT. THAT IS WITH THE SAME QUANTITY OF 0 NE INPUT AND LARGER QUANTITY OF THE OTHER INPUT, LARGER OUTPUT WILL BE PRODUCED.

PROPERTIES OF ISOQUANTS 3. NO TWO ISOQUANTS INTERSECT OR TOUCH EACH OTHER. IF THE TWO ISOQUANTS DO TOUCH OR INTERSECT THAT MEANS THAT A SAME AMOUNT OF TWO INPUTS CAN PRODUCE TWO DIFFERENT LEVELS OF OUTPUT WHICH IS ABSURD.

PROPERTIES OF ISOQUANTS 4. ISOQUANT IS CONVEX TO THE ORIGIN. THIS MEANS THAT THE SLOPE DECLINES FROM LEFT TO RIGHT ALONG THE CURVE. THAT IS WHEN WE GO ON INCREASING THE QUANTITY OF ONE INPUT SAY LABOUR BY REDUCING THE QUANTITY OF OTHER INPUT SAY CAPITAL, WE SEE LESS UNITS OF CAPITAL ARE SACRIFICED FOR THE ADDITIONAL UNITS OF LABOUR.
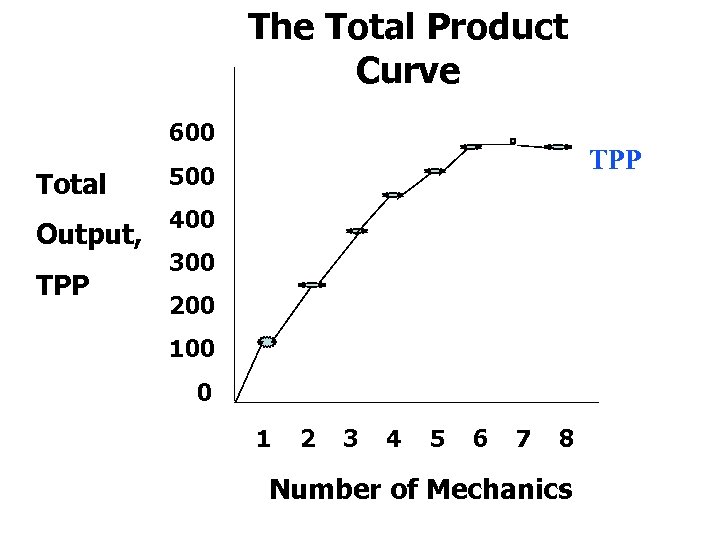
The Total Product Curve 600 Total Output, TPP 500 400 300 200 100 0 1 2 3 4 5 6 7 8 Number of Mechanics
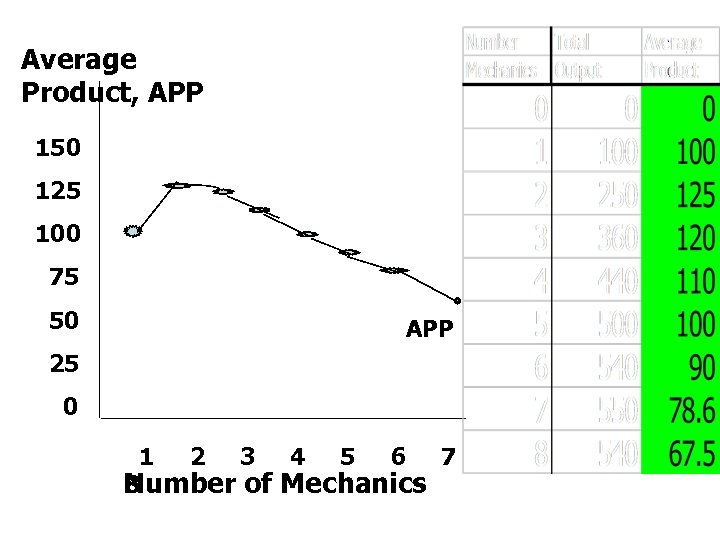
Average Product, APP 150 125 100 75 50 APP 25 0 1 2 3 4 5 6 7 Number of Mechanics 8

Let’s Plot the MPP Schedule We’ll place it on top of the APP schedule so we can compare the two
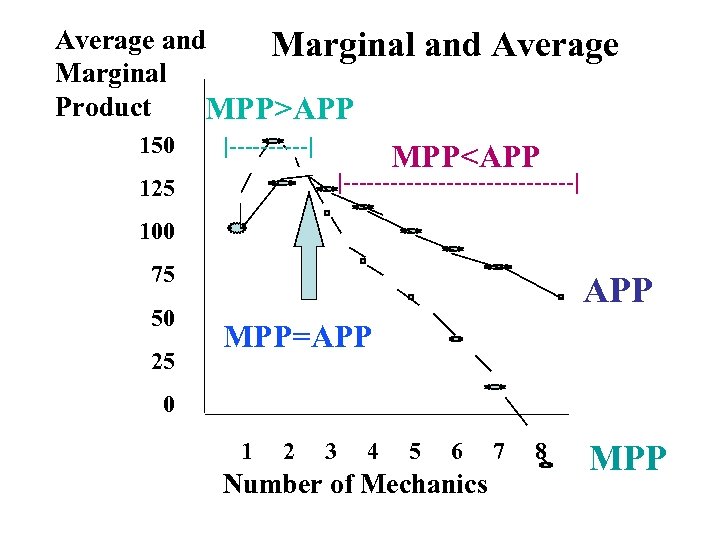
Average and Marginal Product MPP>APP 150 |-----| and Average MPP<APP |---------------| 125 100 75 50 25 APP MPP=APP 0 1 2 3 4 5 6 Number of Mechanics 7 8 MPP

RETURNS TO SCALE • DIMINISHING RETURNS REFER TO RESPONSE OF OUTPUT TO AN INCREASE OF A SINGLE INPUT WHILE OTHER INPUTS ARE HELD CONSTANT. • WE HAVE TO SEE THE EFFECT BY INCREASING ALL INPUTS. • WHAT WOULD HAPPEN IF THE PRODUCTION OF WHEAT IF LAND, LABOUR, FERTILISERS, WATER ETC, . ARE ALL DOUBLED. THIS REFERS TO THE RETURNS TO SCALE OR EFFECT OF SCALE INCREASES OF INPURTS ON THE QUANTITY PRODUCED.

CONSTANT RETURNS TO SCALE • THIS DENOTES A CASE WHERE A CHANGE IN ALL INPUTS LEADS TO A PROPORTIONAL CHANGE IN OUTPUT. • FOR EXAMPLE IF LABOUR, LAND CAPITAL AND OTHER INPUTS DOUBLED, THEN UNDER CONSTANT RETURNS TO SCALE OUTPUT WOULD ALSO DOUBLE.

INCREASING RETURNS TO SCALE • THIS IS ALSO CALLED ECONOMIES OF SCALE. THIS ARISES WHEN AN INCREASE IN ALL INPUTS LEADS TO A MORE-THAN-PROPORTIONAL INCREASE IN THE LEVEL OF OUTPUT. • FOR EXAMPLE AN ENGINEER PLANNING A SMALL SCALE CHEMICAL PLANT WILL GENERALLY FIND THAT BY INCREASING INPUTS OF LABOUR, CAPITAL AND MATERIALS BY 10% WILL INCREASE THE TOTAL OUTPUT BY MORE THAN 10%.

DECREASING RETURNS TO SCALE • THIS OCCURS WHEN A BALANCED INCREASE OF ALL INPUTS LEADS TO A LESS THAN PORPORTIONAL INCREASE IN TOTAL OUTPUT. • IN MANY PROCESS, SCALING UP MAY EVENTUALLY REACH A POINT BEYOND WHIH INEFFICIENCIES SET IN. THESE MIGHT ARISE BECAUSE THE COSTS OF MANAGEMENT OR CONTROL BECOME LARGE. • THIS WAS VERY EVIDENT IN ELECTRICITY GENERATION WHEN PLANTS GREW TOO LARGE, RISK OF PLANT FAILURE INCREASED.

IMPORTANCE OF RETURNS TO SCALE CONCEPT IF AN INDUSTRY IS CHARACTERIZED BY INCREASING RETURNS TO SCALE, THERE WILL BE A TENDENCY FOR EXPANDING THE SIZE OF THE FIRM AND THUS THE INDUSTRY WILL BE DOMINATED BY LARGE FIRMS. THE OPPOSITE WILL BE TRUE IN INDUSTRIES WHERE DECREASING RETURNS TO SCALE PREVAIL. IN CASE OF INDUSTRIES WITH CONSTANT RETURNS TO SCALE, FIRMS OF ALL SIZES WOULD SURVIVE EQUALLY WELL.

FROM PRODUCTION TO COST • TO GET TO WHERE WE REALLY WANT TO BE, WE MUST TRANSLATE THE PRODUCT SCHEDULES AND CURVES TO COSTS. • LET’S ASSUME THE COST PER VARIABLE RESOURCE -- PER WORK -IS $1000 PER WEEK. • ASSUME THIS IS THE ONLY COST.

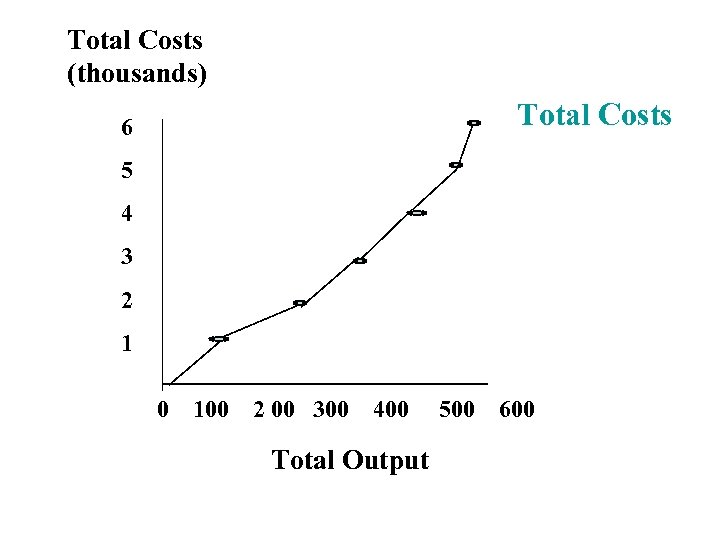
Total Costs (thousands) Total Costs 6 5 4 3 2 1 0 100 2 00 300 400 Total Output 500 600

Average and Marginal • Economists find it useful to talk about three dimensions of something: • Total • Average = per unit • Marginal = incremental



Plot the Average Cost and the Marginal Cost Schedules • Average Cost is the per unit cost: total cost divided by quantity of output • Marginal Cost is the change in total cost divided by the change in total output.

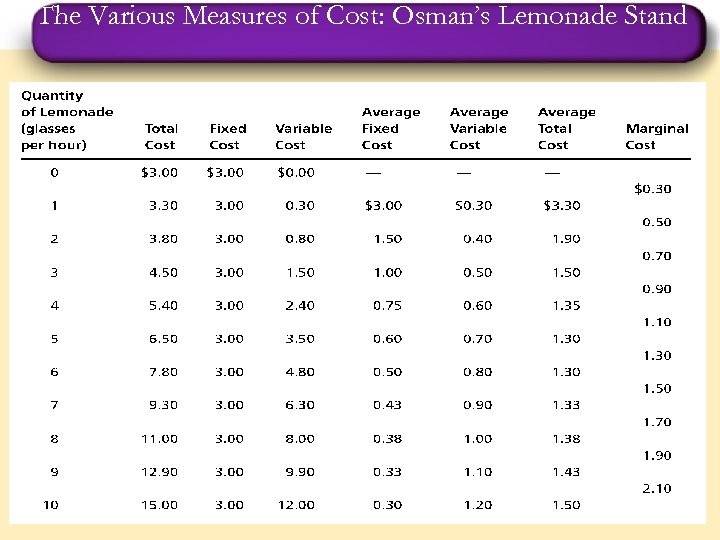
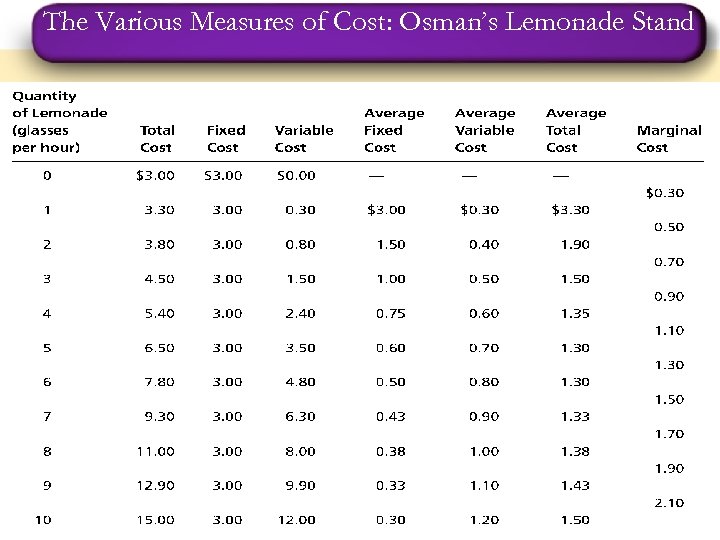
The Various Measures Of Cost n n n Costs of production may be separated into fixed costs and variable costs. Fixed costs are those costs that do not change with the quantity of output produced. Ex: Rent, accountant’s wage, some taxes. . Variable costs are those costs that do change with the quantity of output produced. Ex: Labor, Electricity, Transportation, . . .

Fixed and Variable Costs n Total Costs q Total Fixed Costs (TFC) q Total Variable Costs (TVC) q Total Costs (TC) q TC = TFC + TVC
The Various Measures of Cost: Osman’s Lemonade Stand

Fixed and Variable Costs n Average Costs q q Average costs can be determined by dividing the firm’s costs by the quantity of output it produces. Average cost answers the following question: How much does it cost to produce one unit of a good on average?

Fixed and Variable Costs n Average Costs q q Average Fixed Cost (AFC) = Total Fixed Cost / Qty Average Variable Cost (AVC) = Total Variable Cost / Qty Average Total Costs (ATC) = Total Cost / Qty ATC = AFC + AVC
The Various Measures of Cost: Osman’s Lemonade Stand

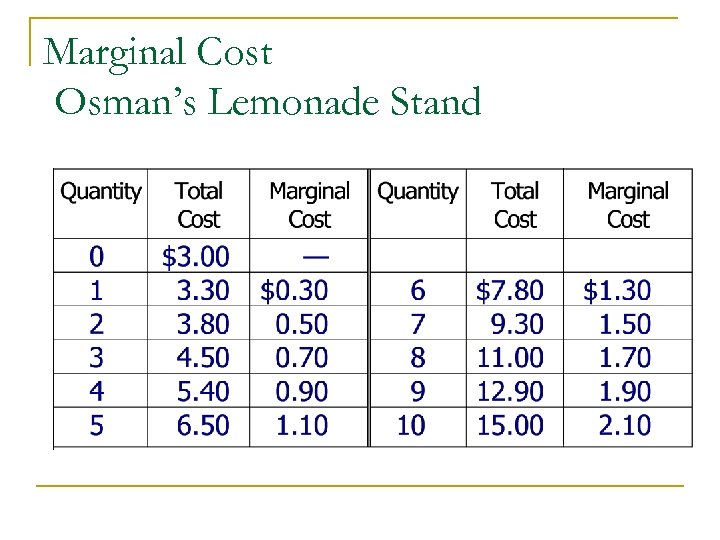
Marginal Cost n Marginal Cost q q Marginal cost (MC) is the additional cost of producing the last unit. Marginal cost helps answer the following question: n How much does it cost to produce an additional unit of output?
Marginal Cost Osman’s Lemonade Stand

Marginal Cost
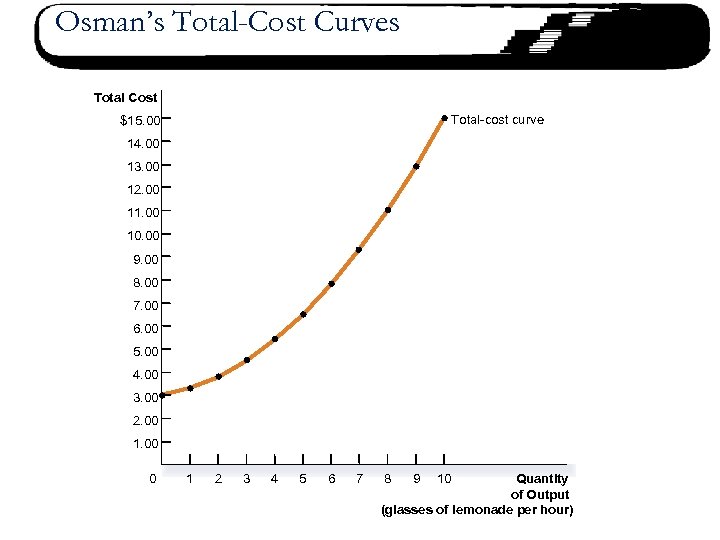
Osman’s Total-Cost Curves Total Cost Total-cost curve $15. 00 14. 00 13. 00 12. 00 11. 00 10. 00 9. 00 8. 00 7. 00 6. 00 5. 00 4. 00 3. 00 2. 00 1. 00 0 1 2 3 4 5 6 7 Quantity of Output (glasses of lemonade per hour) 8 9 10
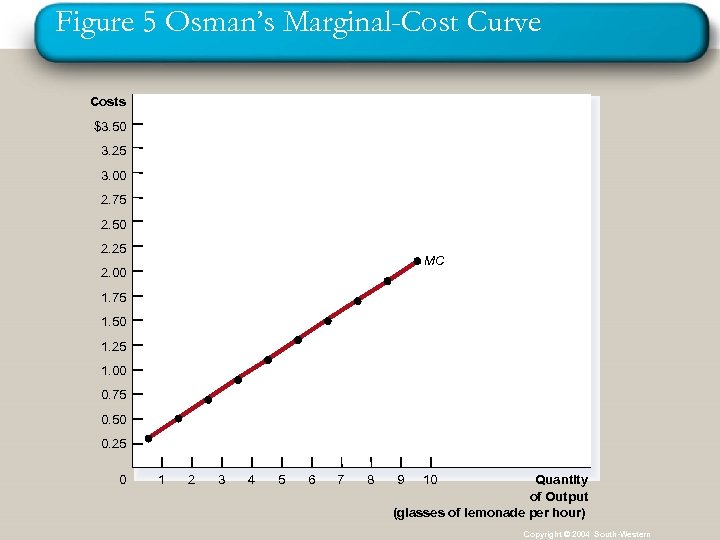
Figure 5 Osman’s Marginal-Cost Curve Costs $3. 50 3. 25 3. 00 2. 75 2. 50 2. 25 MC 2. 00 1. 75 1. 50 1. 25 1. 00 0. 75 0. 50 0. 25 0 1 2 3 4 5 6 7 8 Quantity of Output (glasses of lemonade per hour) 9 10 Copyright © 2004 South-Western

Cost Curves and Their Shapes n Marginal cost increases as we produce more and more q This is due to the property of diminishing marginal product. See example.
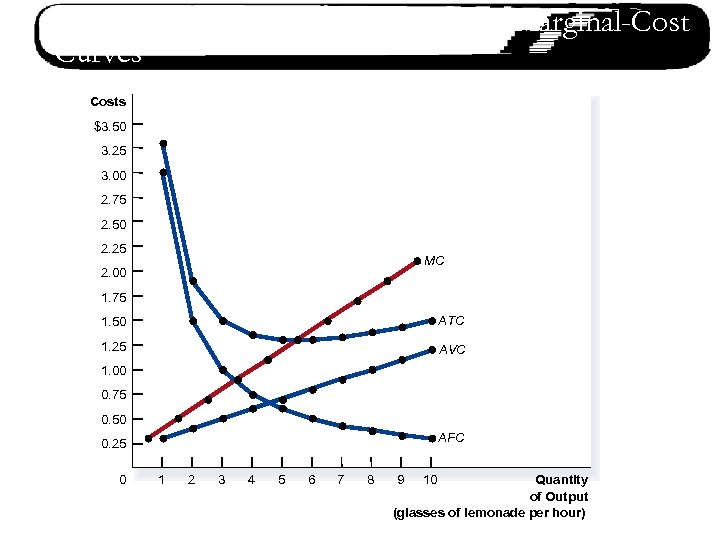
Figure 6 Osman’s Average-Cost and Marginal-Cost Curves Costs $3. 50 3. 25 3. 00 2. 75 2. 50 2. 25 MC 2. 00 1. 75 1. 50 ATC 1. 25 AVC 1. 00 0. 75 0. 50 AFC 0. 25 0 1 2 3 4 5 6 7 8 Quantity of Output (glasses of lemonade per hour) 9 10 Copyright © 2004 South-Western
The Various Measures of Cost: Osman’s Lemonade Stand

Cost Curves and Their Shapes n n The average total-cost (ATC) curve is U-shaped. At very low levels of output, ATC is high because fixed cost is spread over only a few units. ATC declines as output increases because fixed cost is spread over more units. As output increases further, ATC starts rising because average variable cost rises faster than the decline in AFC.

Cost Curves and Their Shapes n The quantity where the firm achieves the lowest average cost is at the minimum point of the U-shaped ATC curve. This quantity is called the efficient scale of the firm.
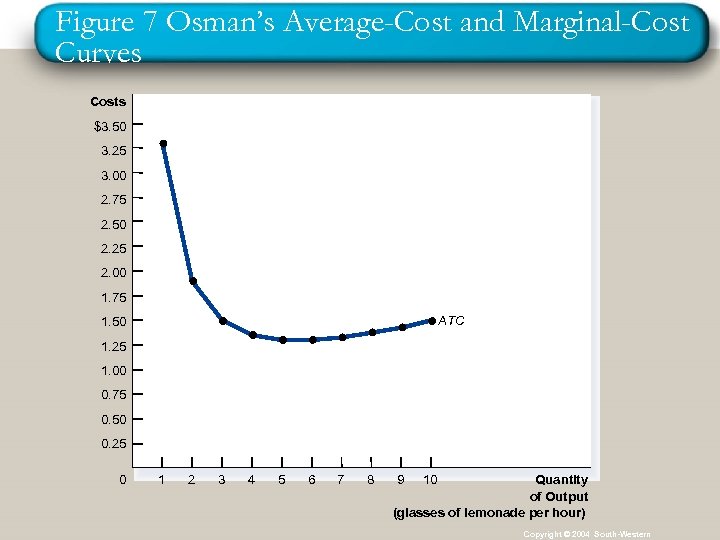
Figure 7 Osman’s Average-Cost and Marginal-Cost Curves Costs $3. 50 3. 25 3. 00 2. 75 2. 50 2. 25 2. 00 1. 75 ATC 1. 50 1. 25 1. 00 0. 75 0. 50 0. 25 0 1 2 3 4 5 6 7 8 Quantity of Output (glasses of lemonade per hour) 9 10 Copyright © 2004 South-Western

Cost Curves and Their Shapes n Relationship between Marginal Cost and Average Total Cost q q Whenever MC is smaller than ATC, ATC is falling. Whenever MC is greater than ATC, ATC is rising. ATC is like your cumulative GPA and MC is like your last semester’s grade average. As a result, MC crosses ATC at the minimum of ATC.
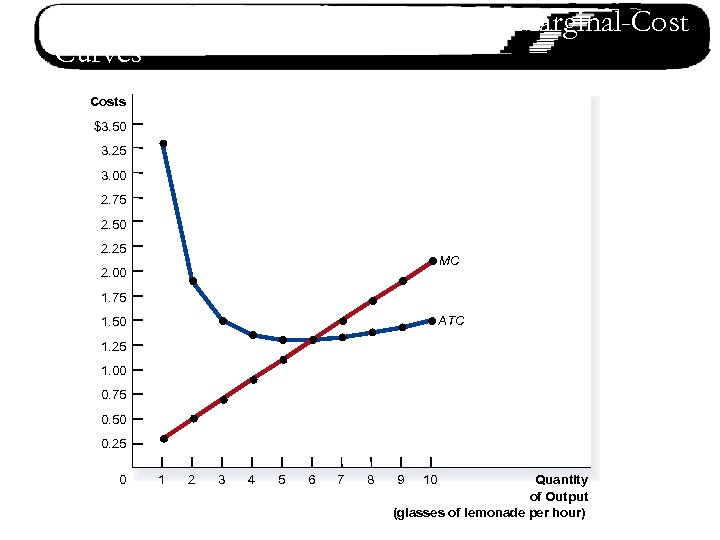
Figure 5 Osman’s Average-Cost and Marginal-Cost Curves Costs $3. 50 3. 25 3. 00 2. 75 2. 50 2. 25 MC 2. 00 1. 75 ATC 1. 50 1. 25 1. 00 0. 75 0. 50 0. 25 0 1 2 3 4 5 6 7 8 Quantity of Output (glasses of lemonade per hour) 9 10 Copyright © 2004 South-Western

Cost Curves and Their Shapes n Summarize Three Important Properties of Cost Curves q q q Marginal cost eventually rises as the quantity of output increases. The ATC curve is U-shaped. The MC curve crosses the ATC curve at the minimum point of ATC.

Costs In The Short Run And In The Long Run n For many firms, the division of total costs between fixed and variable costs depends on the time horizon being considered. q q In the short-run, some costs are fixed (Ex: rent of building and machines), some are variable (labor, energy, raw materials). In the long-run, fixed costs become variable costs (Ex: renting decisions can change, can buy/rent new machines and equipment). All costs are variable in the long-run.

Costs In The Short Run And In The Long Run n Because many costs are fixed in the shortrun but variable in the long-run, a firm’s longrun cost curves are different from its short-run cost curves.
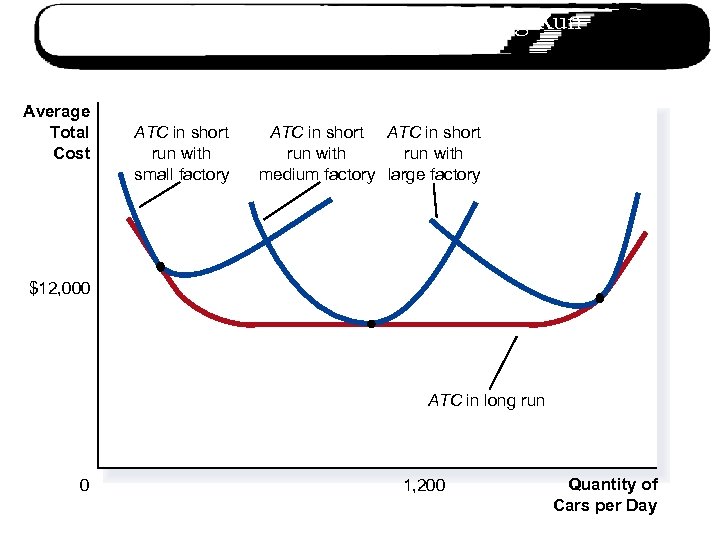
Average Total Cost in the Short and Long Run Average Total Cost ATC in short run with small factory ATC in short run with medium factory large factory $12, 000 ATC in long run 0 1, 200 Quantity of Cars per Day Copyright © 2004 South-Western
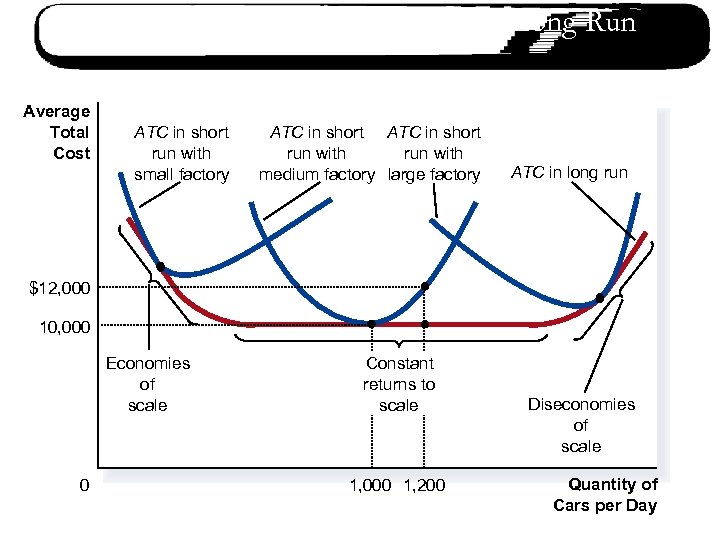
Average Total Cost in the Short and Long Run Average Total Cost ATC in short run with small factory ATC in short run with medium factory large factory ATC in long run $12, 000 10, 000 Economies of scale 0 Constant returns to scale 1, 000 1, 200 Diseconomies of scale Quantity of Cars per Day

Costs versus Size of the Firm n If long-run ATC falls as the quantity of output increases, the firm has Increasing Returns to Scale (=Economies of Scale). n If long-run ATC rises as the quantity of output increases, the firm has Decreasing Returns to Scale (=Diseconomies of Scale). n If long-run ATC stays constant as the quantity of output increases, the firm has Constant Returns to Scale.

Economies and Diseconomies of Scale n The shape of LRATC depends on the type of industry. n Some industries exhibit economies of scale (also called increasing returns to scale) like cable TV, GSM providers, electricity, oil extraction, high-tech goods, etc. Such industries are characterized by high fixed costs. n Some industries show decreasing returns to scale because firms are too big. Coordination problems & bureaucracy. IBM and General Motors are examples.

Long Run Production Functions • All inputs are variable » greatest output from any set of inputs • Q = f( K, L ) is two input example • MP of capital and MP of labor are the derivatives of the production function » MPL = Q / L = Q / L • MP of labor declines as more labor is applied. Also the MP of capital declines as more capital is applied. Slide 100
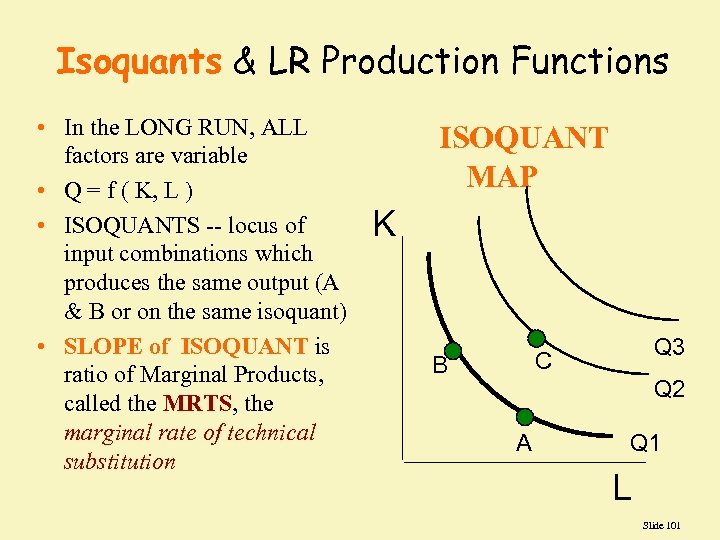
Isoquants & LR Production Functions • In the LONG RUN, ALL factors are variable • Q = f ( K, L ) • ISOQUANTS -- locus of input combinations which produces the same output (A & B or on the same isoquant) • SLOPE of ISOQUANT is ratio of Marginal Products, called the MRTS, the marginal rate of technical substitution ISOQUANT MAP K Q 3 C B Q 2 A Q 1 L Slide 101

Optimal Combination of Inputs • The objective is to minimize cost for a given output • ISOCOST lines are the combination of inputs for a given cost, C 0 Equimarginal Criterion: Produce where MPL/CL = MPK/CK where marginal products per dollar are equal Figure 7. 9 on page 316 • C 0 = CL·L + CK·K • K = C 0/CK - (CL/CK)·L • Optimal where: » MPL/MPK = CL/CK· » Rearranged, this becomes the equimarginal criterion K D at D, slope of isocost = slope of isoquant C(1) L Q(1) Slide 102

Use of the Equimarginal Criterion • Q: Is the following firm EFFICIENT? • A dollar spent on labor produces 3, and a dollar spent on capital produces 2. • Suppose that: USE RELATIVELY » MP L = 30 MORE LABOR! » MPK = 50 • If spend $1 less in capital, » W = 10 (cost of labor) output falls 2 units, but rises » R = 25 (cost of capital) 3 units when spent on labor • Shift to more labor until the • Labor: 30/10 = 3 equimarginal condition holds. • Capital: 50/25 = 2 • That is peak efficiency. • A: No! Slide 103
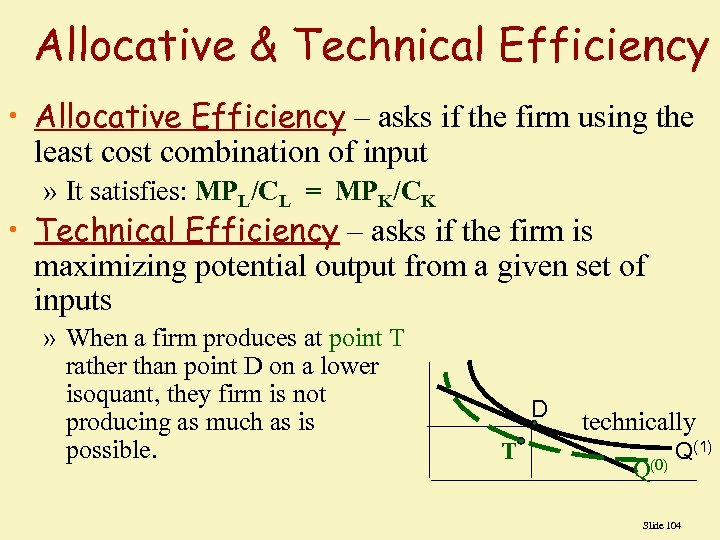
Allocative & Technical Efficiency • Allocative Efficiency – asks if the firm using the least combination of input » It satisfies: MPL/CL = MPK/CK • Technical Efficiency – asks if the firm is maximizing potential output from a given set of inputs » When a firm produces at point T rather than point D on a lower isoquant, they firm is not producing as much as is possible. D T technically Q Q(1) (0) Slide 104
ef65ad9c2d8f6b5861f63df168cb0034.ppt