Theory of Consumer Behavior OVC-Principles of Microeconomics David B. Hamm, MBA, CPA Spring 2003 +
Scenario: Are you hungry? n You’re on a road trip and you’re getting very hungry. You stop at the first place you see, which is one of those burger places selling those tiny square burgers (White Castle, Krystal, etc. ) for 59 cents each: n n n You consume one burger and it tastes wonderful! Burger nirvana! You consume a second burger and it tastes good. You consume a third burger and it tastes fine. You pause a moment before buying a fourth, but you’re still a bit hungry. It tastes…well, OK. You don’t want to buy a fifth burger, but your traveling companion gives one to you, you eat it, and immediately you need to go to the restroom!
Utility Theory In the burger scenario, you have just illustrated several elements of utility theory. n Utility is defined as the level of satisfaction derived from consumption of a good or service n Usually measured by how much we are willing to pay (or give up) to get something. n
Marginal Utility n Marginal utility (MU) is the additional utility derived from consuming one more unit of a good or service n The Law of Diminishing Marginal Utility states that as we consume more of a good/service, the marginal utility gained from each additional unit declines (even if total utility initially increases)
Burgers and Marginal Utility n In the burger scenario (slide one), while we were hungry and wanted to consume additional burgers to maximize total utility (satisfy our hunger), marginal utility (satisfaction) declined with each new burger: n The first burger cost only 59 cents, but we were so hungry, we might have been willing to pay $1. 00 or more for it: MU > P
Burgers and Marginal Utility (2) n n The second burger still cost only 59 cents but we were still pretty hungry—we might have paid, say 90 cents for it. (MU still > P) The third burger might have been worth, say 75 cents to us—still a good buy. (MU > P) By the fourth burger, we paused—it was worth only 59 cents—its price—to us. (MU = P) The fifth burger we wouldn’t therefore pay for. (MU < P) When it was given to us (zero cost) and we consumed it, we regretted it (negative marginal utility, or MU < 0)
Utility Maximization We therefore are willing (normally) to consume a good/service up to the point where MU = Price or MU / P = 1 n In real life, we often make choices among several goods, thus consumer optimum (or the general utility formula) is MU 1/P 1 = MU 2/P 2 etc. for all goods consumed. n
Utility Maximization (2) n n n If the MU of a good is > P, we tend to consume more of that good and less of others until MU declines to the point of MU/P = 1 for all goods consumed. If, due to budget constraints, we can not consume until MU/P = 1 for all goods, we still allocate our limited funds so that MU/P = MU/P for each good. Most of this is intuitive—we don’t solve equations while at the grocery store, but we do mentally allocate our budget among desired goods until we are satisfied with our purchases and then check out.
The Diamond-Water Paradox n Diamonds are very expensive, while water is usually inexpensive. But water is essential to life (daily)—diamonds essential only to a proposal of marriage (hopefully once). So why are diamonds so much more expensive than water? n n Relative scarcity is part of it—diamonds still are rare products, and water usually isn’t. But if you’re stuck in the desert and facing dehydration and death, our values (MU) would change substantially.
Diamond-Water Paradox (2) n Therefore, we consume water to the point where MU / P and diamonds also to the point where MU / P. n n A single glass of water has low utility but also has a very low price, whereas a single diamond has high utility but also a high price. Consumer optimum formula still applies: MUwater/Pwater = MU diamond/Pdiamond
Consumer Surplus n In the burger scenario, we were willing to pay a higher price for the first three burgers but the market price was only 59 cents. The difference between what we would pay and what we actually pay is consumer surplus. n If MU > P for any good, consumer surplus exists, until MU = P.
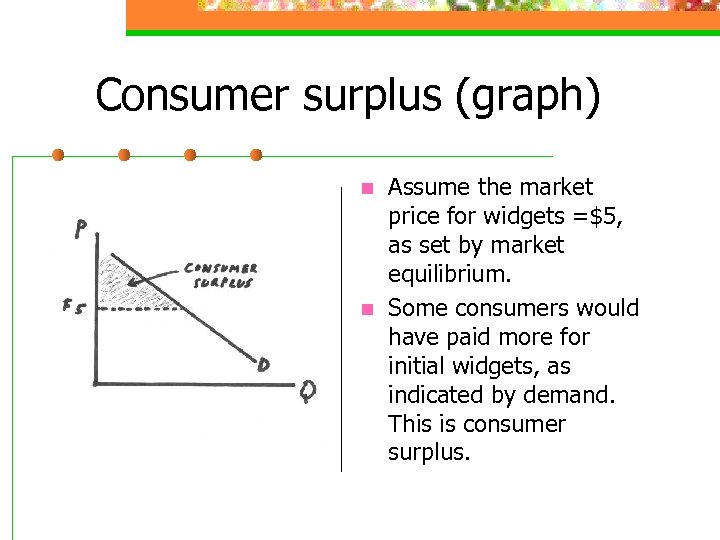
Consumer surplus (graph) n n Assume the market price for widgets =$5, as set by market equilibrium. Some consumers would have paid more for initial widgets, as indicated by demand. This is consumer surplus.
Скачать презентацию Theory of Consumer Behavior OVC-Principles of Microeconomics David
495720d0907fc890981e0d62afb28aeb.ppt