4f8f1ae7a0bf4bea35e899f0f94c9932.ppt
- Количество слайдов: 42
 Theorem Proving and Model Checking in PVS 15 -820 A PVS – An Introduction Edmund Clarke Daniel Kroening Carnegie Mellon University 1
Theorem Proving and Model Checking in PVS 15 -820 A PVS – An Introduction Edmund Clarke Daniel Kroening Carnegie Mellon University 1
 Theorem Proving and Model Checking in PVS Outline • • Theorem provers Why PVS? Topics for this semester Short introduction to the PVS language • The PVS workflow • A short proof 2
Theorem Proving and Model Checking in PVS Outline • • Theorem provers Why PVS? Topics for this semester Short introduction to the PVS language • The PVS workflow • A short proof 2
 Theorem Proving and Model Checking in PVS Theorem Provers • Stores theorems and establishes their correctness • What kind of theorems? – First order – Second order / higher order • How to establish the correctness? – Completely automated – Semi-automated – Interactive (manual) 3
Theorem Proving and Model Checking in PVS Theorem Provers • Stores theorems and establishes their correctness • What kind of theorems? – First order – Second order / higher order • How to establish the correctness? – Completely automated – Semi-automated – Interactive (manual) 3
 Theorem Proving and Model Checking in PVS Theorem Provers There is a wide range of theorem provers • • Higher order: ALF, Alfa, Coq, HOL, PVS Logical Frameworks: Isabelle, LF, Twelf Inductive: ACL 2, Inka Automated: Gandalf, TPS, Otter, Setheo, SPASS • EQP, Maude 4
Theorem Proving and Model Checking in PVS Theorem Provers There is a wide range of theorem provers • • Higher order: ALF, Alfa, Coq, HOL, PVS Logical Frameworks: Isabelle, LF, Twelf Inductive: ACL 2, Inka Automated: Gandalf, TPS, Otter, Setheo, SPASS • EQP, Maude 4
 Theorem Proving and Model Checking in PVS Theorem Provers • The most commonly used Theorem Provers, from systems verification point of view – HOL: Floating Point Verification (Intel) – ACL 2: Floating Point Verification (AMD) – PVS: NASA/Do. D, e. g. , Space Shuttle flight control requirements specification It also does Floating Point Units. • PVS is… – Higher order – Interactive 5
Theorem Proving and Model Checking in PVS Theorem Provers • The most commonly used Theorem Provers, from systems verification point of view – HOL: Floating Point Verification (Intel) – ACL 2: Floating Point Verification (AMD) – PVS: NASA/Do. D, e. g. , Space Shuttle flight control requirements specification It also does Floating Point Units. • PVS is… – Higher order – Interactive 5
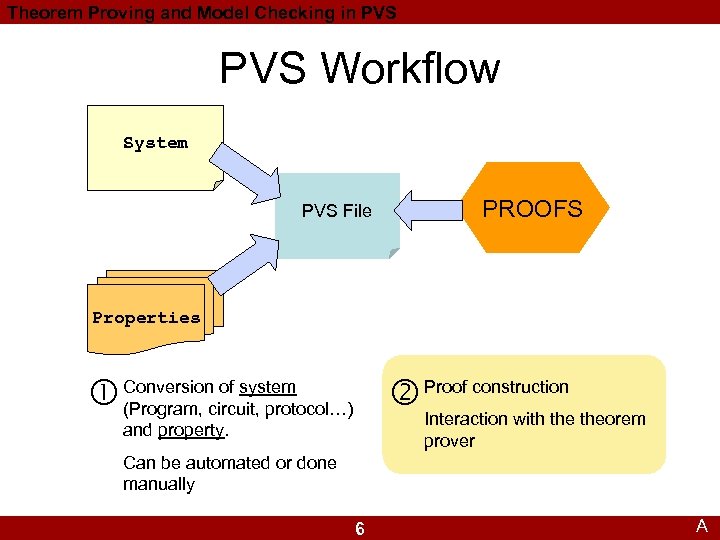 Theorem Proving and Model Checking in PVS Workflow System PVS File PROOFS Properties of system Conversioncircuit, protocol…) Proof construction (Program, Interaction with theorem prover and property. Can be automated or done manually 6 A
Theorem Proving and Model Checking in PVS Workflow System PVS File PROOFS Properties of system Conversioncircuit, protocol…) Proof construction (Program, Interaction with theorem prover and property. Can be automated or done manually 6 A
 Theorem Proving and Model Checking in PVS Why PVS? • Why PVS and not some other theorem prover? From PVS website: “PVS is a large and complex system and it takes a long while to learn to use it effectively. You should be prepared to invest six months to become a moderately skilled user” 7 A
Theorem Proving and Model Checking in PVS Why PVS? • Why PVS and not some other theorem prover? From PVS website: “PVS is a large and complex system and it takes a long while to learn to use it effectively. You should be prepared to invest six months to become a moderately skilled user” 7 A
 Theorem Proving and Model Checking in PVS Why PVS? • Why PVS and not some other theorem prover? • Other (strong) theorem provers probably worse • The PVS language is close to “normal” notation – Not LISP! • PVS is interactive – why not an automated theorem prover? – Decidable logics often not rich enough, or inconvenient – Semi-automated theorem provers usually don’t tell what is wrong, experience and knowledge about internals required 8
Theorem Proving and Model Checking in PVS Why PVS? • Why PVS and not some other theorem prover? • Other (strong) theorem provers probably worse • The PVS language is close to “normal” notation – Not LISP! • PVS is interactive – why not an automated theorem prover? – Decidable logics often not rich enough, or inconvenient – Semi-automated theorem provers usually don’t tell what is wrong, experience and knowledge about internals required 8
 Theorem Proving and Model Checking in PVS Topics for this Semester • PVS – Installation – Proof Interaction • Language Basics – Type Checking – Recursion – Lambda Notation – Abstract Data Types 9
Theorem Proving and Model Checking in PVS Topics for this Semester • PVS – Installation – Proof Interaction • Language Basics – Type Checking – Recursion – Lambda Notation – Abstract Data Types 9
 Theorem Proving and Model Checking in PVS Topics for this Semester • Specification using PVS – Prelude, Libraries – State Machines – Tabular Specifications – How to get “systems” into PVS • Hardware • Software 10
Theorem Proving and Model Checking in PVS Topics for this Semester • Specification using PVS – Prelude, Libraries – State Machines – Tabular Specifications – How to get “systems” into PVS • Hardware • Software 10
 Theorem Proving and Model Checking in PVS Topics for this Semester • Proofs – Induction – Real Numbers – Abstraction of Infinite State Transition Systems • Proof Automation – Rewriting – Write your own decision procedure! – Model Checking as Rule of Inference 11
Theorem Proving and Model Checking in PVS Topics for this Semester • Proofs – Induction – Real Numbers – Abstraction of Infinite State Transition Systems • Proof Automation – Rewriting – Write your own decision procedure! – Model Checking as Rule of Inference 11
 Theorem Proving and Model Checking in PVS The PVS Language • There are two languages 1. The language to write definitions and theorems (“definition language“) 2. The language to prove theorems (“proof language”) They have nothing to do with each other • The definition language looks like “normal math” (translator to Latex built in) • The proof language looks like LISP 12
Theorem Proving and Model Checking in PVS The PVS Language • There are two languages 1. The language to write definitions and theorems (“definition language“) 2. The language to prove theorems (“proof language”) They have nothing to do with each other • The definition language looks like “normal math” (translator to Latex built in) • The proof language looks like LISP 12
 Theorem Proving and Model Checking in PVS The PVS Definition Language • Main language elements – Declarations • Types • Constants – Expressions over these types – Expressions of Boolean types may be a formula – Formulae are theorems or axioms – Declarations and formulae are grouped into theories 13
Theorem Proving and Model Checking in PVS The PVS Definition Language • Main language elements – Declarations • Types • Constants – Expressions over these types – Expressions of Boolean types may be a formula – Formulae are theorems or axioms – Declarations and formulae are grouped into theories 13
 Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type Type Declarations f 1: THEOREM FORALL (a, b: integer): a+b=b+a Expressions f 2: AXIOM constant 1=constant 2 END class_theory 14 A
Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type Type Declarations f 1: THEOREM FORALL (a, b: integer): a+b=b+a Expressions f 2: AXIOM constant 1=constant 2 END class_theory 14 A
 Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type f 1: THEOREM FORALL (a, b: integer): a+b=b+a Formulae f 2: AXIOM constant 1=constant 2 END class_theory 15 A
Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type f 1: THEOREM FORALL (a, b: integer): a+b=b+a Formulae f 2: AXIOM constant 1=constant 2 END class_theory 15 A
 Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type f 1: THEOREM FORALL (a, b: integer): a+b=b+a f 2: AXIOM constant 1=constant 2 END class_theory 16 Declarations
Theorem Proving and Model Checking in PVS The PVS Definition Language class_theory: THEORY BEGIN my_type: NONEMPTY_TYPE constant 1, constant 2: my_type f 1: THEOREM FORALL (a, b: integer): a+b=b+a f 2: AXIOM constant 1=constant 2 END class_theory 16 Declarations
 Theorem Proving and Model Checking in PVS Axioms vs. Theorems • Axioms are assumed to be true • Dangerous! • Avoid axioms, use constant declarations instead: class_theory: THEORY BEGIN c: integer = 3 c: AXIOM c=3 END class_theory Left hand side is conservative 17
Theorem Proving and Model Checking in PVS Axioms vs. Theorems • Axioms are assumed to be true • Dangerous! • Avoid axioms, use constant declarations instead: class_theory: THEORY BEGIN c: integer = 3 c: AXIOM c=3 END class_theory Left hand side is conservative 17
 Theorem Proving and Model Checking in PVS Types • PVS has a very rich type concept – Uninterpreted type declaration: numbers: TYPE numbers: NONEMPTY_TYPE – Interpreted type declaration Introduce names for type expressions posint: TYPE={ i: integer | i > 0} 18
Theorem Proving and Model Checking in PVS Types • PVS has a very rich type concept – Uninterpreted type declaration: numbers: TYPE numbers: NONEMPTY_TYPE – Interpreted type declaration Introduce names for type expressions posint: TYPE={ i: integer | i > 0} 18
 Theorem Proving and Model Checking in PVS Types PVS comes with • boolean – FALSE, TRUE • Number types – real, rational, integer, natural • string • Ordinals 19
Theorem Proving and Model Checking in PVS Types PVS comes with • boolean – FALSE, TRUE • Number types – real, rational, integer, natural • string • Ordinals 19
 Theorem Proving and Model Checking in PVS Type Expressions • Function Types [ t 1, …, tn -> t ] Sugar for that: FUNCTION[ t 1, …, tn -> t ] ARRAY[ t 1, …, tn -> t ] Note that ti and t may be function types as well! 20
Theorem Proving and Model Checking in PVS Type Expressions • Function Types [ t 1, …, tn -> t ] Sugar for that: FUNCTION[ t 1, …, tn -> t ] ARRAY[ t 1, …, tn -> t ] Note that ti and t may be function types as well! 20
 Theorem Proving and Model Checking in PVS Expressions • Constants – Given by their name, as used in the declaration – Numbers (1, 2, 3, …) are actually identifiers and can even be overloaded – If name is ambiguous, use identifier: : type 21
Theorem Proving and Model Checking in PVS Expressions • Constants – Given by their name, as used in the declaration – Numbers (1, 2, 3, …) are actually identifiers and can even be overloaded – If name is ambiguous, use identifier: : type 21
 Theorem Proving and Model Checking in PVS Expressions • Function Applications f(x) – Tons of Syntactic sugar for that, don’t be confused – Binary operator symbols y * z is the same as *(y, z) 22
Theorem Proving and Model Checking in PVS Expressions • Function Applications f(x) – Tons of Syntactic sugar for that, don’t be confused – Binary operator symbols y * z is the same as *(y, z) 22
 Theorem Proving and Model Checking in PVS Expressions • Functions PVS comes with – Boolean AND &, OR, IMPLIES =>, WHEN, IFF <=> – IF c THEN a ELSE b IF: [boolean, T, T -> T] – (COND: sugar for IF THEN ELSE) – Numeric operators +, -, *, /, ^, <, <=, >, >= 23
Theorem Proving and Model Checking in PVS Expressions • Functions PVS comes with – Boolean AND &, OR, IMPLIES =>, WHEN, IFF <=> – IF c THEN a ELSE b IF: [boolean, T, T -> T] – (COND: sugar for IF THEN ELSE) – Numeric operators +, -, *, /, ^, <, <=, >, >= 23
 Theorem Proving and Model Checking in PVS Expressions • Binding Expressions – Quantifiers EXISTS (x: T): p(x) FORALL (y: T): q(y) 24
Theorem Proving and Model Checking in PVS Expressions • Binding Expressions – Quantifiers EXISTS (x: T): p(x) FORALL (y: T): q(y) 24
 Theorem Proving and Model Checking in PVS Expressions • Binding Expressions – Lambda: unnamed functions LAMBDA (x: int): x+1 Type of that: [ int -> int ] class_theory: THEORY BEGIN f: [int->int] = LAMBDA (x: int): x+1 f(x: int): int = x+1 END class_theory 25 A
Theorem Proving and Model Checking in PVS Expressions • Binding Expressions – Lambda: unnamed functions LAMBDA (x: int): x+1 Type of that: [ int -> int ] class_theory: THEORY BEGIN f: [int->int] = LAMBDA (x: int): x+1 f(x: int): int = x+1 END class_theory 25 A
 Theorem Proving and Model Checking in PVS Recursion • Lambda cannot be used for recursion • Only named functions allow recursion • No mutual recursion factorial(x: nat): RECURSIVE nat = IF x=0 THEN 1 ELSE factorial(x-1)*x ENDIF MEASURE (LAMBDA (x: nat): x) Used to prove that the function is total 26 A
Theorem Proving and Model Checking in PVS Recursion • Lambda cannot be used for recursion • Only named functions allow recursion • No mutual recursion factorial(x: nat): RECURSIVE nat = IF x=0 THEN 1 ELSE factorial(x-1)*x ENDIF MEASURE (LAMBDA (x: nat): x) Used to prove that the function is total 26 A
 Theorem Proving and Model Checking in PVS Expressions • LET Expressions LET i: T=e 1 IN e 2 – Useful for avoiding redundancy if e 1 is used many times in e 2 – Sugar for LAMBDA (i: T): e 2)(e 1) – Example LET x=2 IN x*y is (LAMBDA x: x*y)(2) 27
Theorem Proving and Model Checking in PVS Expressions • LET Expressions LET i: T=e 1 IN e 2 – Useful for avoiding redundancy if e 1 is used many times in e 2 – Sugar for LAMBDA (i: T): e 2)(e 1) – Example LET x=2 IN x*y is (LAMBDA x: x*y)(2) 27
 Theorem Proving and Model Checking in PVS Expressions • Override Expressions e WITH [(i 1): =v 1, (i 2): =v 2, …] – Sugar for LAMBDA x: IF x=i 1 THEN v 1 ELSIF x=i 2 THEN v 2 … ELSE e(x) ENDIF – Also for records and tuples 28
Theorem Proving and Model Checking in PVS Expressions • Override Expressions e WITH [(i 1): =v 1, (i 2): =v 2, …] – Sugar for LAMBDA x: IF x=i 1 THEN v 1 ELSIF x=i 2 THEN v 2 … ELSE e(x) ENDIF – Also for records and tuples 28
 Theorem Proving and Model Checking in PVS Expressions • LET and WITH useful for some sequential program constructs! int f(int i) { int a[10]={ 0, … }; . . . a[i]=5; . . . return a[0]; } f(i: int): int= LET a 1=LAMBDA (x: below(10)): 0 IN. . . LET a 2=a 1 WITH [(i): =5] IN. . . ai(0) 29
Theorem Proving and Model Checking in PVS Expressions • LET and WITH useful for some sequential program constructs! int f(int i) { int a[10]={ 0, … }; . . . a[i]=5; . . . return a[0]; } f(i: int): int= LET a 1=LAMBDA (x: below(10)): 0 IN. . . LET a 2=a 1 WITH [(i): =5] IN. . . ai(0) 29
 Theorem Proving and Model Checking in PVS Expressions • Set Expressions – In PVS, sets are represented using their characteristic function [ T -> boolean ] same as setof[T] – Set expressions: { x: T | p(x) } For sets a, b over T: Union: a OR b Intersection: a AND b 30
Theorem Proving and Model Checking in PVS Expressions • Set Expressions – In PVS, sets are represented using their characteristic function [ T -> boolean ] same as setof[T] – Set expressions: { x: T | p(x) } For sets a, b over T: Union: a OR b Intersection: a AND b 30
 Theorem Proving and Model Checking in PVS Some Syntactic Sugar • Tuple types [ t 1, …, tn ] • Tuple expressions ( e 1, …, en ) • Comes with projections PROJ_1, PROJ_2, . . . , PROJ_n 31
Theorem Proving and Model Checking in PVS Some Syntactic Sugar • Tuple types [ t 1, …, tn ] • Tuple expressions ( e 1, …, en ) • Comes with projections PROJ_1, PROJ_2, . . . , PROJ_n 31
 Theorem Proving and Model Checking in PVS Example stacks 1: THEORY BEGIN stack: TYPE = [int, ARRAY[int->int]] empty: stack = (0, (LAMBDA (j: int): 0)) size(s: stack): int = PROJ_1(s) elements(s: stack): ARRAY[int->int] = PROJ_2(s) push(x: int, s: stack): stack = (size(s)+1, elements(s)How about WITH [(size(s)): =x]) a “struct”? pop(s: stack): stack = (size(s)-1, elements(s)) END stacks 1 32 A
Theorem Proving and Model Checking in PVS Example stacks 1: THEORY BEGIN stack: TYPE = [int, ARRAY[int->int]] empty: stack = (0, (LAMBDA (j: int): 0)) size(s: stack): int = PROJ_1(s) elements(s: stack): ARRAY[int->int] = PROJ_2(s) push(x: int, s: stack): stack = (size(s)+1, elements(s)How about WITH [(size(s)): =x]) a “struct”? pop(s: stack): stack = (size(s)-1, elements(s)) END stacks 1 32 A
 Theorem Proving and Model Checking in PVS Some Syntactic Sugar • Record types [# a 1: t 1, …, an: tn #] • Record expressions (# a 1: =e 1, …, an: =en #) • Comes with projections a 1, a 2, . . . , an • Or: e`ai 33
Theorem Proving and Model Checking in PVS Some Syntactic Sugar • Record types [# a 1: t 1, …, an: tn #] • Record expressions (# a 1: =e 1, …, an: =en #) • Comes with projections a 1, a 2, . . . , an • Or: e`ai 33
 Theorem Proving and Model Checking in PVS Example stacks 2: THEORY BEGIN stack: TYPE = [# size: int, elements: ARRAY[int->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: int): 0) #) push(x: int, s: stack): stack = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack): stack = (# size: =s`size-1, elements: =s`elements #) END stacks 2 What about the empty stack? 34 A
Theorem Proving and Model Checking in PVS Example stacks 2: THEORY BEGIN stack: TYPE = [# size: int, elements: ARRAY[int->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: int): 0) #) push(x: int, s: stack): stack = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack): stack = (# size: =s`size-1, elements: =s`elements #) END stacks 2 What about the empty stack? 34 A
 Theorem Proving and Model Checking in PVS Subtypes { x: T | p(x)} • p must be of type [ T -> boolean ] • Sugar for that: (p) • This type contains all elements x of T for which p(x) is true • E. g. , define domain of integer division: { x: integer | x/=0 } • Makes type equivalence undecidable 35
Theorem Proving and Model Checking in PVS Subtypes { x: T | p(x)} • p must be of type [ T -> boolean ] • Sugar for that: (p) • This type contains all elements x of T for which p(x) is true • E. g. , define domain of integer division: { x: integer | x/=0 } • Makes type equivalence undecidable 35
 Theorem Proving and Model Checking in PVS Subtypes • Subtypes in binding expressions – Forall, exists: forall (i: int | i>10): … – Lambda: class_theory: THEORY BEGIN f(x: int | x/=0): real = 1/x END class_theory f: [ {x: int | x/=0 }->real] = LAMBDA (x: int | x/=0): 1/x END class_theory 36
Theorem Proving and Model Checking in PVS Subtypes • Subtypes in binding expressions – Forall, exists: forall (i: int | i>10): … – Lambda: class_theory: THEORY BEGIN f(x: int | x/=0): real = 1/x END class_theory f: [ {x: int | x/=0 }->real] = LAMBDA (x: int | x/=0): 1/x END class_theory 36
 Theorem Proving and Model Checking in PVS Example stacks 3: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[nat->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: nat): 0) #) push(x: int, s: stack): { s: stack | s`size>=1 } = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack | s`size>=1): stack = (# size: =s`size-1, elements: =s`elements #) END stacks 3 Properties? 37 A
Theorem Proving and Model Checking in PVS Example stacks 3: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[nat->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: nat): 0) #) push(x: int, s: stack): { s: stack | s`size>=1 } = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack | s`size>=1): stack = (# size: =s`size-1, elements: =s`elements #) END stacks 3 Properties? 37 A
 Theorem Proving and Model Checking in PVS Example stacks 3: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[nat->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: nat): 0) #) push(x: int, s: stack): { s: stack | s`size>=1 } = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack | s`size>=1): stack = (# size: =s`size-1, elements: =s`elements #) Does this work? push_pop: THEOREM FORALL (s: stack, x: int): pop(push(x, s))=s END stacks 3 38 A
Theorem Proving and Model Checking in PVS Example stacks 3: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[nat->int] #] empty: stack = (# size: =0, elements: =(LAMBDA (j: nat): 0) #) push(x: int, s: stack): { s: stack | s`size>=1 } = (# size: =s`size+1, elements: =s`elements WITH [(s`size): =x] #) pop(s: stack | s`size>=1): stack = (# size: =s`size-1, elements: =s`elements #) Does this work? push_pop: THEOREM FORALL (s: stack, x: int): pop(push(x, s))=s END stacks 3 38 A
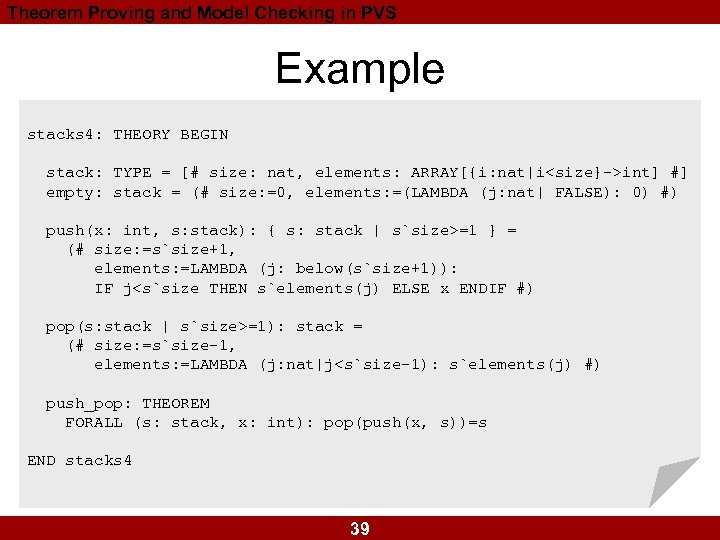 Theorem Proving and Model Checking in PVS Example stacks 4: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[{i: nat|i
Theorem Proving and Model Checking in PVS Example stacks 4: THEORY BEGIN stack: TYPE = [# size: nat, elements: ARRAY[{i: nat|i
 Theorem Proving and Model Checking in PVS Proof? • • • How to argue? pop(push(x, s)) = s Let’s to the size component and the elements component separately Size: pop(push(x, s))`size = s`size – Expand definition of pop: push(x, s)`size - 1 = s`size – Expanding the definition of push results in s`size+1 -1=s`size 40
Theorem Proving and Model Checking in PVS Proof? • • • How to argue? pop(push(x, s)) = s Let’s to the size component and the elements component separately Size: pop(push(x, s))`size = s`size – Expand definition of pop: push(x, s)`size - 1 = s`size – Expanding the definition of push results in s`size+1 -1=s`size 40
 Theorem Proving and Model Checking in PVS Proof? (2) • Elements: pop(push(x, s))`elements = s`elements – Expand definition of pop: ( (j: nat|j
Theorem Proving and Model Checking in PVS Proof? (2) • Elements: pop(push(x, s))`elements = s`elements – Expand definition of pop: ( (j: nat|j
 Theorem Proving and Model Checking in PVS What next… • Webpage! – Installation instructions for PVS – Further reading – Homework assignment 42
Theorem Proving and Model Checking in PVS What next… • Webpage! – Installation instructions for PVS – Further reading – Homework assignment 42


