88dd927a49eab688f96d9fb1176c359e.ppt
- Количество слайдов: 61

Theorem proving Alexander Serebrenik 1
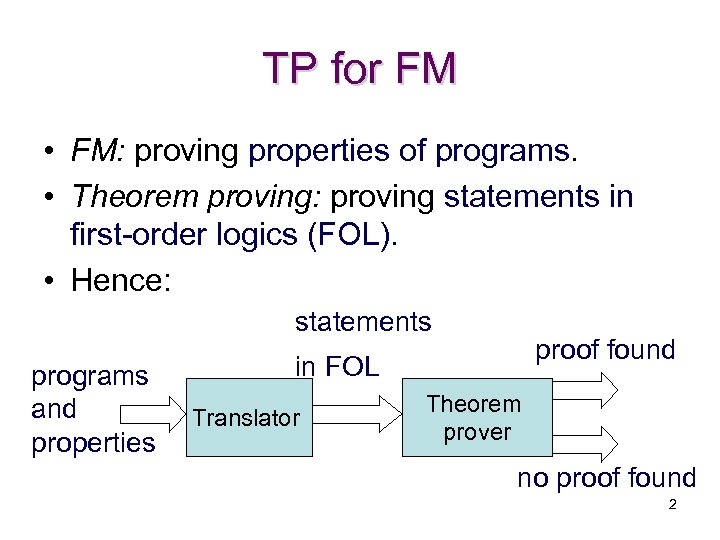
TP for FM • FM: proving properties of programs. • Theorem proving: proving statements in first-order logics (FOL). • Hence: statements programs and properties proof found in FOL Translator Theorem prover no proof found 2
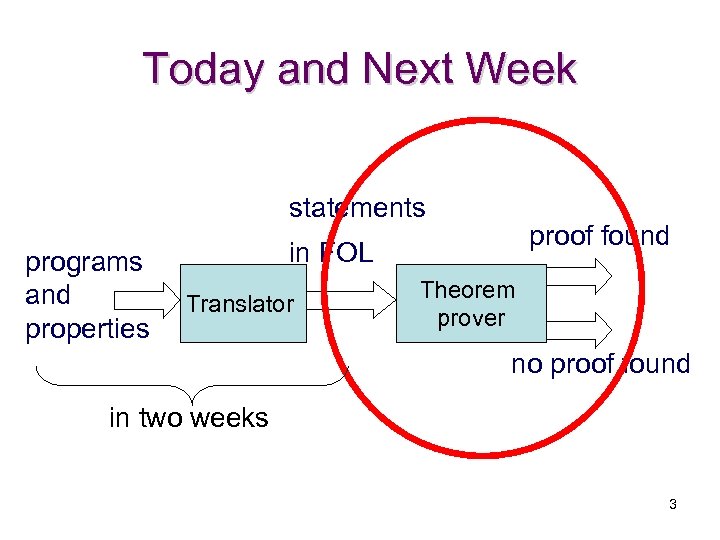
Today and Next Week statements programs and properties proof found in FOL Translator Theorem prover no proof found in two weeks 3

Propositional Calculus – Reminder • Predicates: p, q, r, … • Connectors: – (“and”), – (“or”), – (“not”), – (“implies”) • E. g. (p q) r 4

First Order Logics – reminder • • Constants: ‘John Doe’, 1984, 3. 14159… Variables: x, y, z, … Function symbols: f, g, h, … Predicates: p, q, r, … • Term: h(x), father. Of(‘John Doe’) • Atomic sentence: married(father. Of(‘John Doe’), ‘Jane Smith’) 5

Connectors and Quantifiers • • Connectors: , , , married(x, ‘Jane’) rich(x) Quantifiers: , x (married(x, ‘Jane’) rich(x)) • QQ: “Everybody needs somebody” A. x y needs(x, y) C. x y needs(x, y) B. x y needs(x, y) D. x y needs(x, y) 6

Variables: Free and Bound • Intuition: variables that appear between () after , are called bound, otherwise they are called free. • QQ: Which variables are free in the following sentence? x ((p(x, y) q(x)) z (r(v, z) s(z))) 7

Questions so far? • If these notions are not familiar… • If you are not sure which variables are free in x (p(x, y) z q(z, x))… • If you do not remember whether (p(x) q(y)) is equivalent to p(x) q(y) ü Check logics textbooks! 8

Some Sentences Are Always True • If x and y are negative then x*y is positive. • Any prime number greater than two is odd. • We call this tautology and denote╞ φ – φ - sentence 9

╞φ? • Check whether for all variable substitutions φ is evaluated to true. 10

Alternative • We need a proof calculus – number of syntactic inference rules – when applied to axioms can produce φ • Even better: reduce φ to axioms by applying the rules! • QQ: Why is the second option better? 11

Proofs • If φ can be reduced to axioms by applying the rules we write ├φ • Proof = series of reduction steps • φ is provable 12

Correctness Properties for ├ • Proof calculus should satisfy: • Soundness: If├ φ then ╞ φ – if something has been proved, it holds. • Completeness: If ╞ φ then ├ φ – if something holds, it can be proven. 13

System G • a proof calculus for propositional calculus / firstorder logics • sound and complete • basis for automated theorem provers We • will see the axioms and the inference rules • apply them to a number of examples • discuss automation of the approach 14
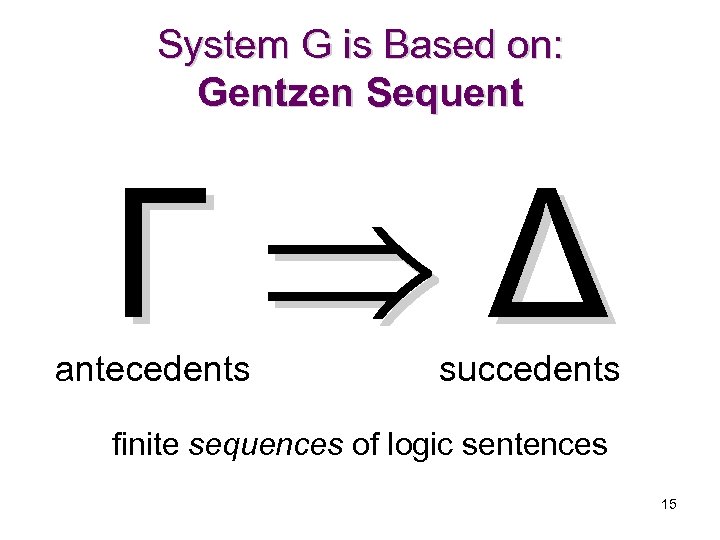
System G is Based on: Gentzen Sequent Γ Δ antecedents succedents finite sequences of logic sentences 15

Intuition Let Γ be A 1, …, An , Δ be B 1, …, Bm Γ Δ corresponds to ╞ ((A 1 … An) (B 1 … Bm)) 16

System G: Axioms • Γ Δ is an axiom if Γ Δ ≠ • QQ: Explain the choice of the axioms. • Hint: recall the intuition behind Γ Δ 17

System G: Inference Rules • Depend on the outermost connector of quantifier. • Conjunction (1): • A, B are arbitrary sentences • Γ, Δ, Λ are sequences of sentences • Read upwards: – replace an antecedent A B by two antecedents A and B 18

System G: Try It Yourself! • QQ: Prove (A B A) • Proof: 19

System G: : right • What if we need to prove A B? • We need to prove two statements: A and B Ø Replace one sequent by two: 20

System G: Try It Yourself! • QQ: Prove (A, B A B) • Proof: 21
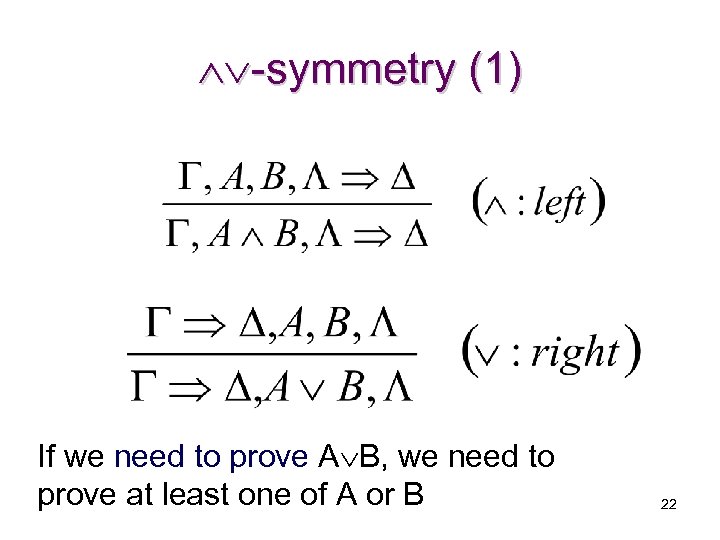
-symmetry (1) If we need to prove A B, we need to prove at least one of A or B 22

-symmetry (2) If we know A B, we either know A or we know B. 23

Negation 24

Implication: Try Yourself! Group A Group B Reminder: A B is equivalent to A B. 25

Implication: Group A Hence 26

Implication: Group B Hence 27
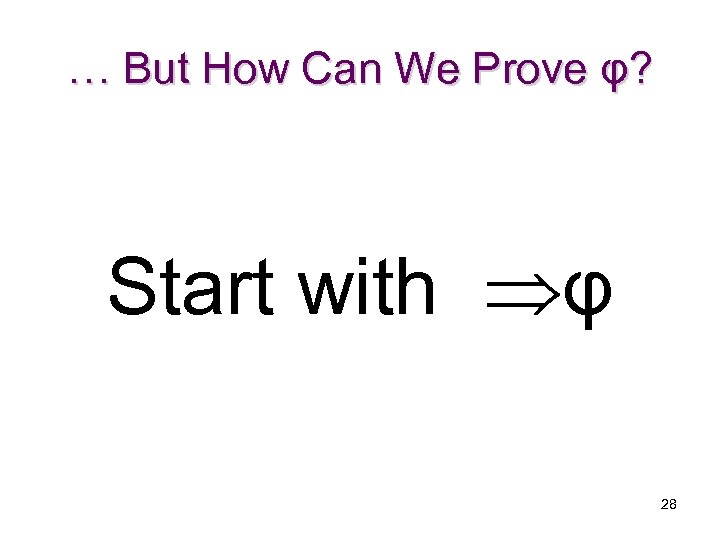
… But How Can We Prove φ? Start with φ 28
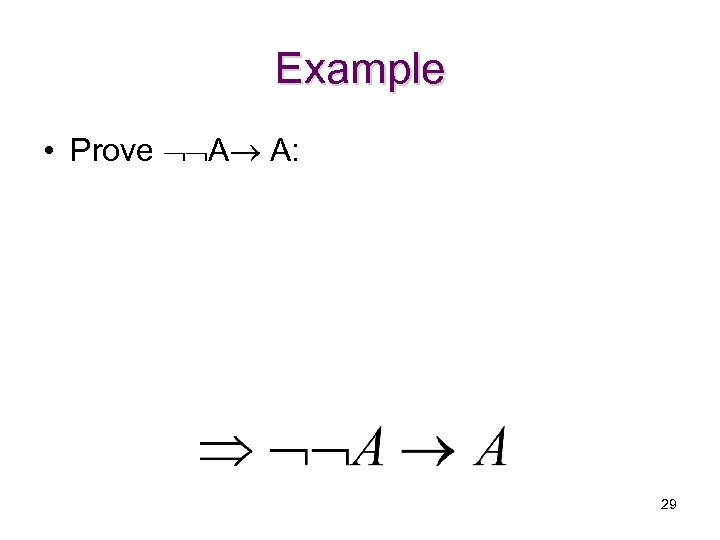
Example • Prove A A: 29

Summary So Far • System G: – based on the notion of a Gentzen sequent – sequent: Γ Δ • Axioms: Γ Δ is an axiom if Γ Δ ≠ • For propositional calculus: 8 inference rules ({ , , , } * {left, right}) • For First-Order Logics: 4 more to come. 30

G for Propositional Calculus • Sound and complete for propositional calculus. • There exists an algorithm that given a sequent: – always terminates – proves the sequent if and only if it is a tautology – based on the notion of a proof tree, i. e. , a tree with nodes labelled by sequents 31

Algorithm (1) algo search(Γ Δ) T : = one-node tree labeled with Γ Δ while exists a leaf of T that can be expanded Copy. T : = T for each leaf node of Copy. T if the node is not an axiom expand(node, T) if all leaves are axioms write(‘T is the proof of Γ Δ’) else write(‘Γ Δ is not a tautology’) 32

Algorithm (2) algo expand(node, T) let node be labeled A 1, … , An B 1, … , Bm S : = one-node tree labeled with A 1, … , An B 1, … , Bm for i=1 to n if nonatomic(Ai) then apply 2 all(Ai, left, S) for i=1 to m if nonatomic(Ai) then apply 2 all(Ai, right, S) replace node in T by S 33

Algorithm: Let Us Try It! Tree T Tree S 34

Algorithm: Let Us Try It! Tree T Tree S 35

Algorithm: Let Us Try It! Tree T Both leaves are axioms! Hence, T is the proof of 36

Algorithm: QQ • To prove that our algorithm terminates we have to find a certain value that decreases from a parent node to each one of the children nodes. • What is this value? 37

Towards FOL: : left • – if we know that x A(x) holds, then we can chose any term t (not containing x) and replace x by t. – A[t/x] denotes replacement of all x’s in A by t QQ: Why do we keep x A? 38

Towards FOL: : right • – if we need to prove that x A holds, we can take any term t (not containing x) and replace x A by A[t/x]. – if the proof of A[t/x] succeeds, then we have also proved x A – t is not necessarily unique, so we keep x A 39

But what if we know x A? • We still do not know for which x does A hold! How can we guess? • We do not need to guess! A new (unused) variable: let y be such that A[y/x] holds! 40

And If We Need to Prove x A? • The same idea works! • If A holds for a new unused variable y, then it holds for any value 41

QQ: Why Should y Be New? • Otherwise, we loose soundness! • Give an example. 42

Summary: System G for Quantifiers 43

QQ Group A: Prove x A A if A does not contain x. Group B: Prove A x A if A does not contain x. 44

System G for FOL • Sound and complete • There exists an algorithm that given a sequent: – proves the sequent if and only if it is a tautology – extends our previous algorithm • However, termination is no longer guaranteed 45
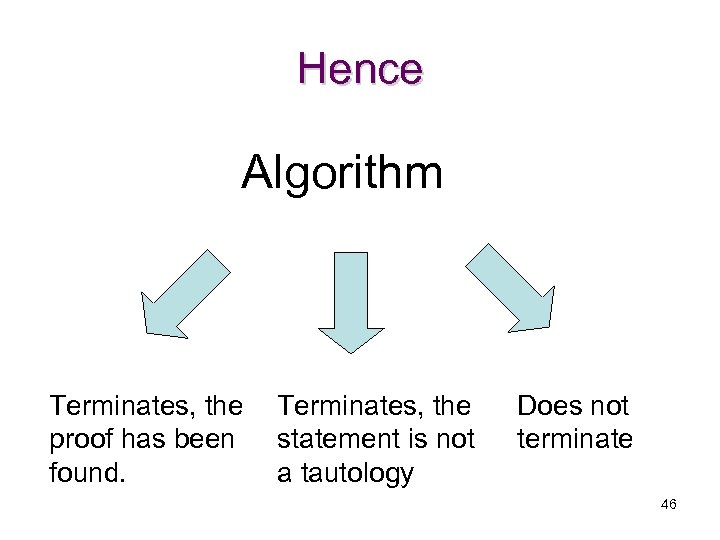
Hence Algorithm Terminates, the proof has been found. Terminates, the statement is not a tautology Does not terminate 46

Even more bad news • There exists no algorithm for FOL that – always terminates, and – proves the sequent if and only if it is a tautology. • In other words, the problem of deciding whether an FOL formula is a tautology is recursively enumerable, but not corecursively enumerable. 47

Reasons for Non-Termination (1) • Repetitive application of ( : left), ( : right). – it is useless to chose the same t twice for the same A. – for each term t keep a list of x. A and x. A such that t has been used for the replacement in ( : left) or ( : right). 48

Reasons for Non-Termination (2) • As we have function symbols we have infinitely many terms to choose from: {a, f(a), f(f(a)), f(f(f(a))), …} – either try all of them in some order – or leave the choice to a human 49

How Shall We Adapt the Algorithm? (1) • List of variables {x 0, x 1, …, xn} appearing in Γ Δ • List of variables for ( : right) and ( : left): {y 1, y 2, …} – disjoint from {x 0, x 1, …, xn} – a variable is removed from the list every time these rules are applied 50

How Shall We Adapt the Algorithm? (2) • Structure TERM of pairs <t, S> – S = a list of x. A and x. A such that t has been used for the replacement in ( : left) or ( : right). – initially: <c, nil>, where c is • a constant or a free variable appearing in Γ Δ, if exists • y 0, otherwise • List AVAIL of terms for ( : left) and ( : right): – AVAIL 0 - terms from free variables, constants (if exist) or y 0 (otherwise), and function symbols – AVAILi - terms containing yi constructed from free variables, constants, y 1, …, yi, and function symbols 51

How Shall We Adapt the Algorithm? (3) • ( : right) and ( : left): – Remove yi from {y 1, y 2, …} – Add yi to TERM – Remove yi from AVAILi • ( : left) and ( : right): – All terms from TERM are available – Add first element from AVAILi to TERM and remove it from AVAILi 52

Complete Algorithm? • See handouts 53

We Have FOL, But We Need More G= • We would like to compare terms, using = s y S S u o d n m e t n a c d p m o te le for any f for any P 54

System G=: QQ axiom 55

P Can Be =! 56

Example: Symmetry of = T: 57

Automation • For propositional calculus – complete – the user can make reasoning more efficient • choice of A 1, …, An B 1, …, Bm to apply an inference rule. • For FOL and FOL= – only partial automation possible: • choice of a term for the substitution. • choice of A 1, …, An B 1, …, Bm to apply an inference rule. 58

Summary (1) • Proving properties of programs is based on proving logic formulae. • To prove a formula one needs proof calculus. • Proof calculus should be sound and complete. • System G is based on the notion of a sequent. 59

Summary (2) • Sequent Γ Δ – Γ, Δ are finite sequences of sentences • System G for propositional calculus is sound and complete. – there is a proof algorithm that always terminates. • System G for FOL is sound and complete. – proof algorithm can go forever. • System G= for FOL= is sound and complete. – proof algorithm can go forever. 60

Next Lecture: PVS • Prototype Verification System – Developed at SRI International – Open Source (GPL) since 1993 – Runs on Linux/Solaris/Mac – Uses Emacs as Interface – Supports System G reasoning… – and much, much more! • We will use it, so install it at your laptops! 61
88dd927a49eab688f96d9fb1176c359e.ppt