The wandering photon a probabilistic model of wave

The wandering photon, a probabilistic model of wave propagation MASSIMO FRANCESCHETTI University of California at Berkeley

From a long view of the history of mankind — seen from, say ten thousand years from now — there can be little doubt that the most significant event of the 19 th century will be judged as Maxwell’s discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade. Richard Feynman The true logic of this world is in the calculus of probabilities. James Clerk Maxwell

Maxwell Equations in complex environments • No closed form solution • Use approximated numerical solvers

We need to characterize the channel • Power loss • Bandwidth • Correlations

Simplified theoretical model solved analytically Everything should be as simple as possible, but not simpler.

Simplified theoretical model solved analytically 2 parameters: h density g absorption

The photon’s stream

The wandering photon Walks straight for a random length Stops with probability g Turns in a random direction with probability (1 -g)

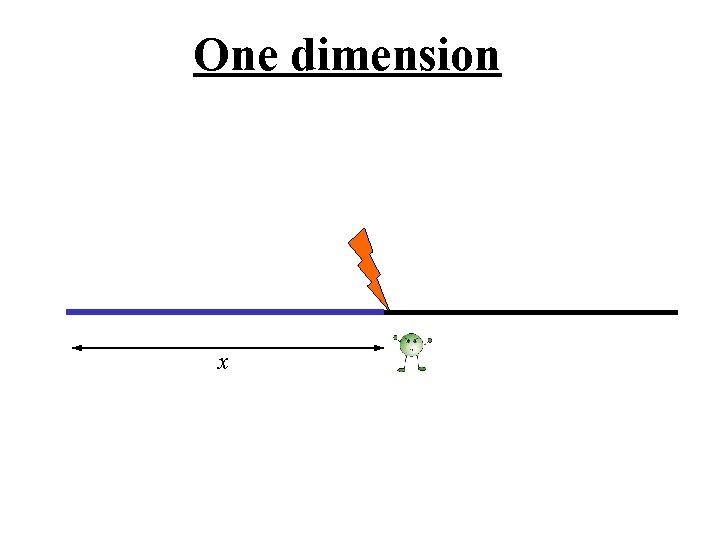
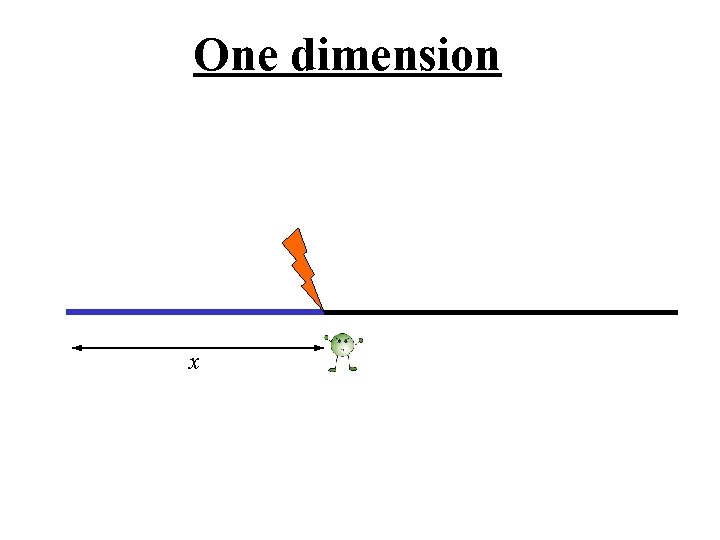
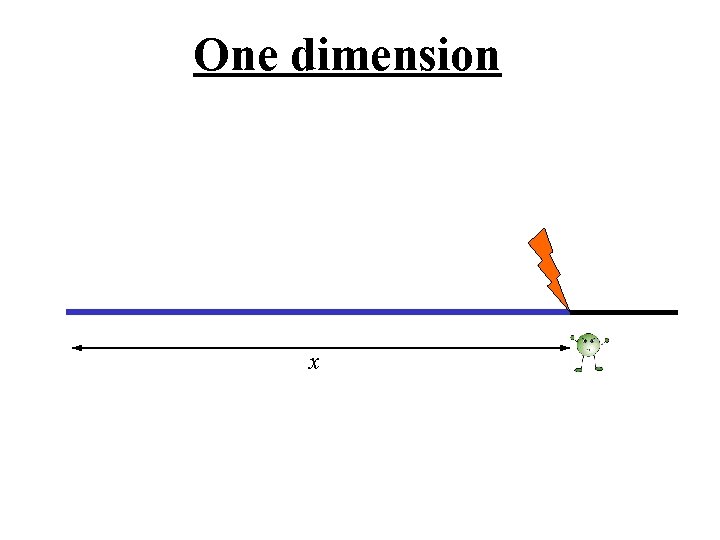
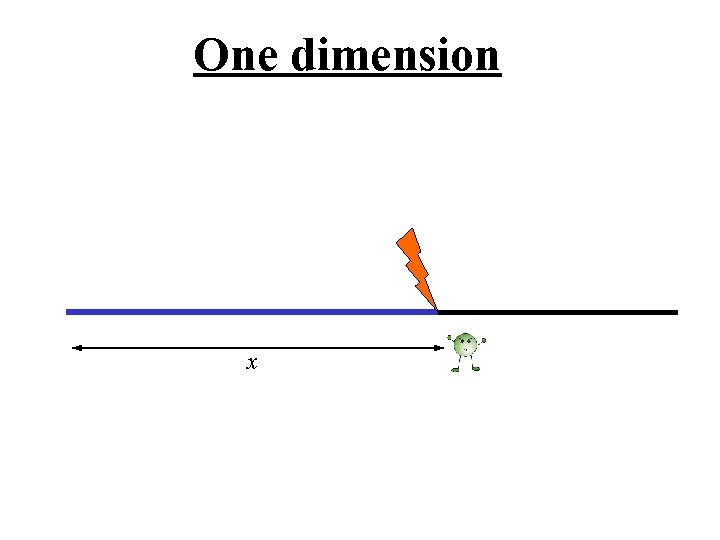
One dimension

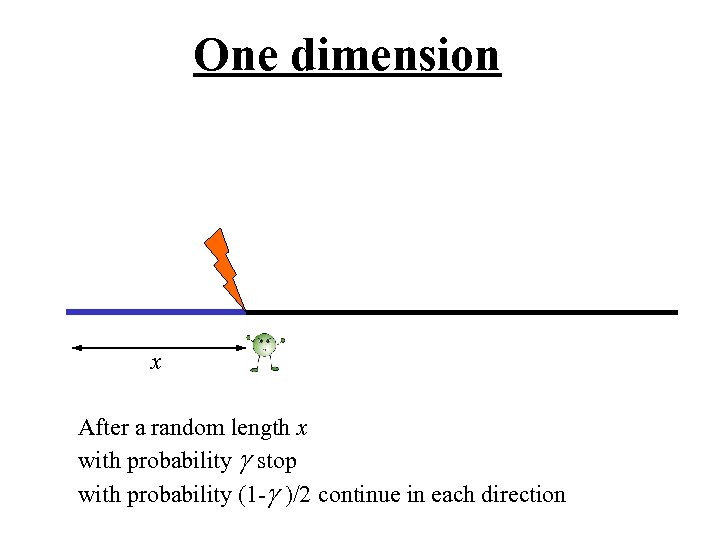
One dimension x After a random length x with probability g stop with probability (1 -g )/2 continue in each direction

One dimension x

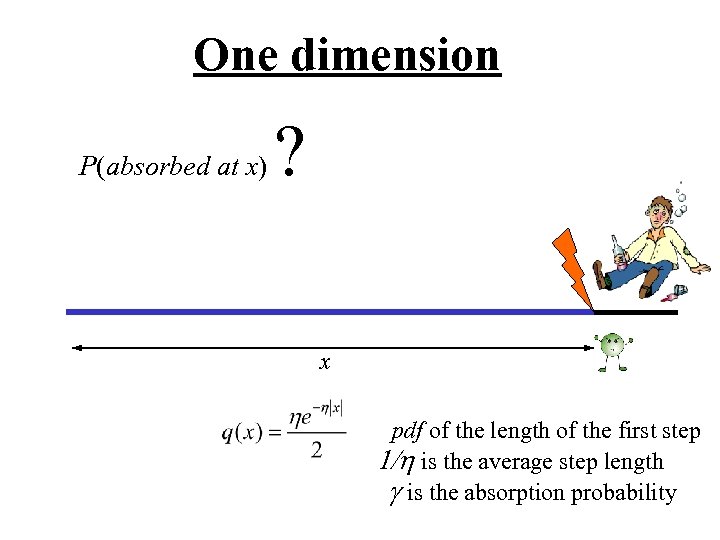
One dimension P(absorbed at x) ? x pdf of the length of the first step 1/h is the average step length g is the absorption probability

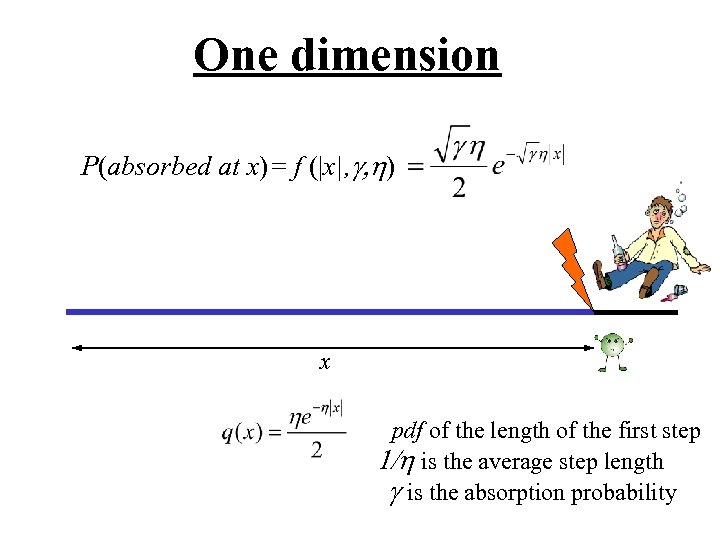
One dimension P(absorbed at x) = f (|x|, g, h) x pdf of the length of the first step 1/h is the average step length g is the absorption probability

The sleepy drunk in higher dimensions

The sleepy drunk in higher dimensions After a random length, with probability g stop with probability (1 -g ) pick a random direction

The sleepy drunk in higher dimensions

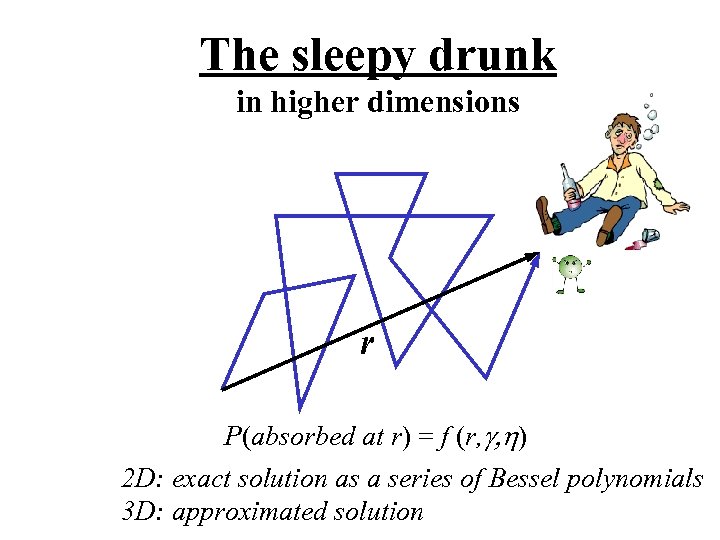
The sleepy drunk in higher dimensions r P(absorbed at r) = f (r, g, h) 2 D: exact solution as a series of Bessel polynomials 3 D: approximated solution

Derivation (2 D) pdf of hitting an obstacle at r in the first step pdf of being absorbed at r Stop first step Stop second step Stop third step

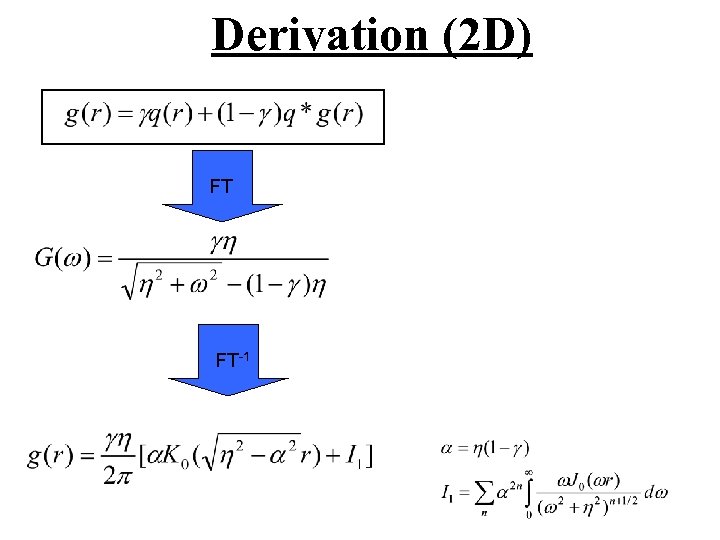
Derivation (2 D) FT FT-1

Derivation (2 D) The integrals in the series I 1 are Bessel Polynomials!

Derivation (2 D) Closed form approximation:

Relating f (r, g, h) to the power received each photon is a sleepy drunk, how many photons reach a given distance?

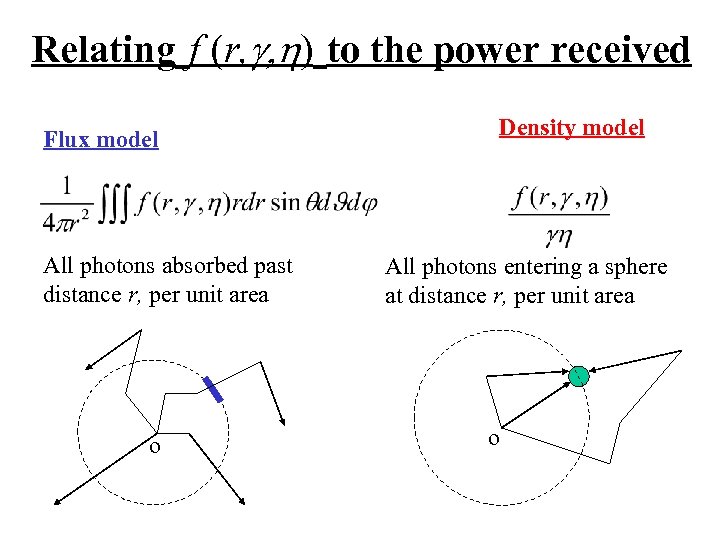
Relating f (r, g, h) to the power received Flux model All photons absorbed past distance r, per unit area o Density model All photons entering a sphere at distance r, per unit area o

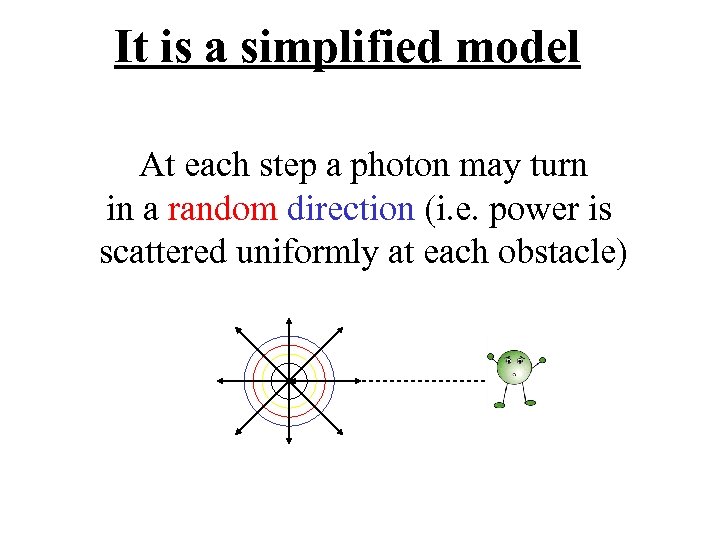
It is a simplified model At each step a photon may turn in a random direction (i. e. power is scattered uniformly at each obstacle)

Validation Random walks Classic approach wave propagation in random media relates Model with losses analytic solution comparison Experiments

Propagation in random media small scattering objects Transport theory Ishimaru A. , 1978. Wave propagation and scattering in random Media. Academic press. Chandrasekhar, S. , 1960, Radiative Transfer. Dover. Ulaby, F. T. and Elachi, C. (eds), 1990. Radar Polarimetry for Geoscience Applications. Artech House.

Isotropic source uniform scattering obstacles

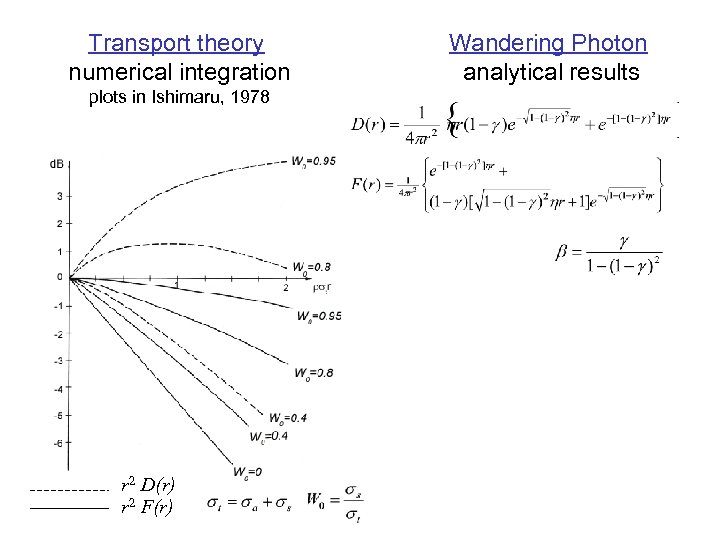
Transport theory numerical integration plots in Ishimaru, 1978 r 2 D(r) r 2 F(r) Wandering Photon analytical results

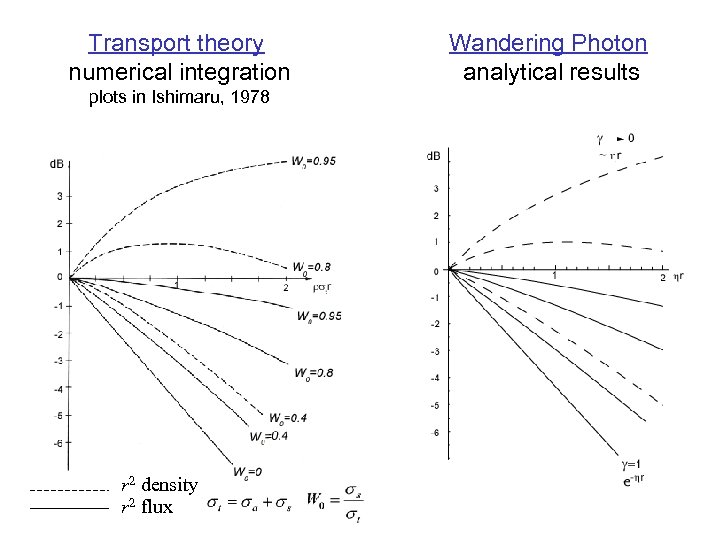
Transport theory numerical integration plots in Ishimaru, 1978 r 2 density r 2 flux Wandering Photon analytical results

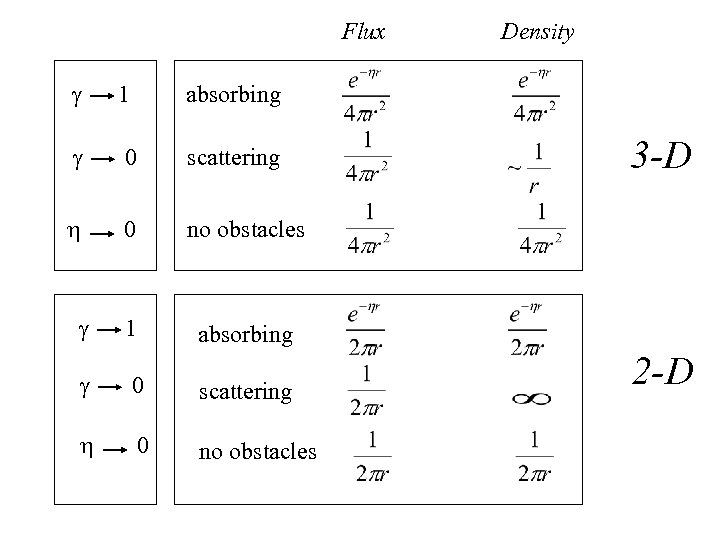
Flux g 1 absorbing g 0 scattering h 0 no obstacles Density 3 -D 2 -D

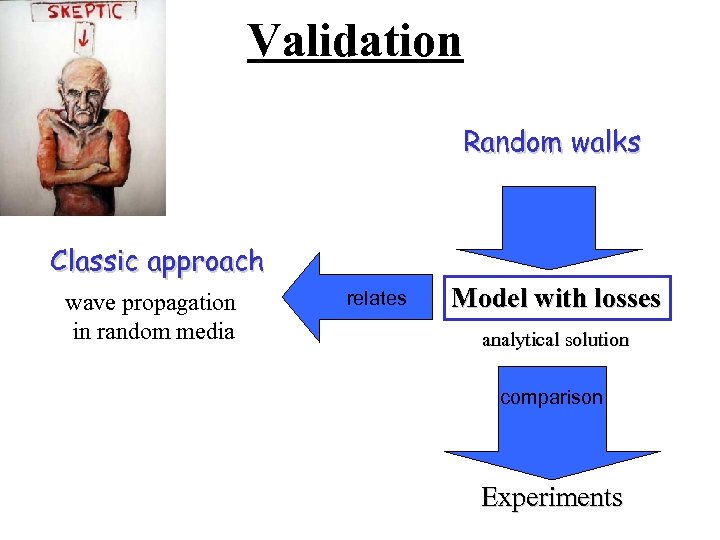
Validation Random walks Classic approach wave propagation in random media relates Model with losses analytical solution comparison Experiments

Urban microcells Collected in Rome, Italy, by Antenna height: 6 m Power transmitted: 6. 3 W Frequency: 900 MHZ Measured average received power over 50 measurements Along a path of 40 wavelengths (Lee method)

Data Collection location

Collected data

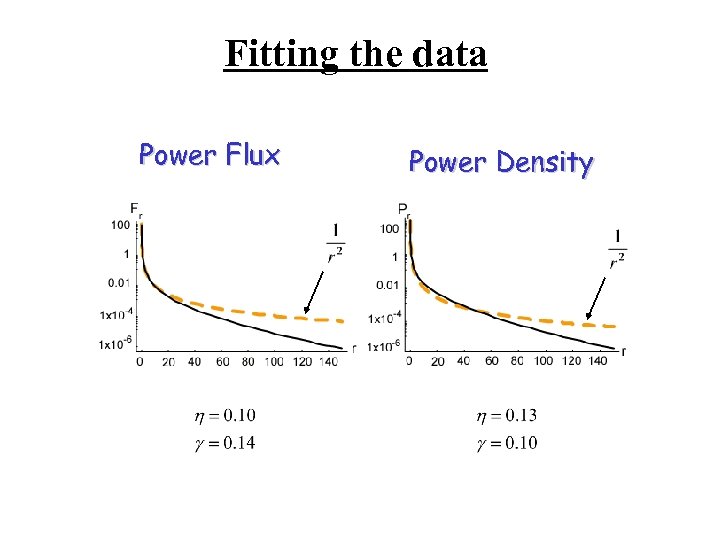
Fitting the data Power Flux Power Density

Simplified formula (d. B/m losses at large distances) based on theoretical, wandering photon model

Power Loss empirical formulas Cellular systems Hata (1980) Microcellular systems Double regression formulas Typical values:

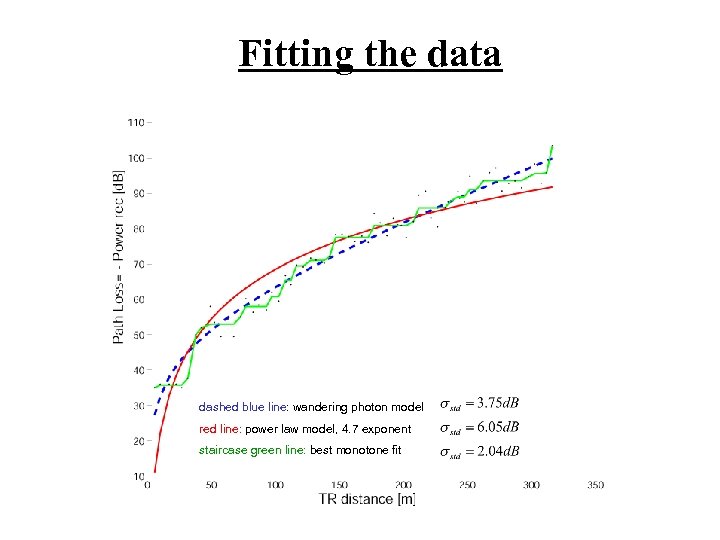
Fitting the data dashed blue line: wandering photon model red line: power law model, 4. 7 exponent staircase green line: best monotone fit

Simplified formula (d. B/m losses at large distances) based on theoretical, wandering photon model Transport capacity of an ad hoc wireless network L. Xie and P. R. Kumar “A network information theory for wireless Communication”

The wandering photon can do more

We need to characterize the channel • Power loss • Bandwidth • Correlations

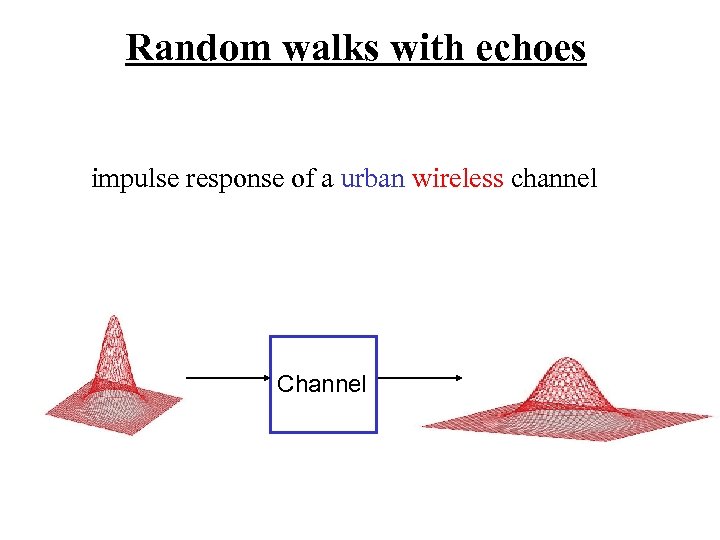
Random walks with echoes impulse response of a urban wireless channel Channel

Impulse response |r 4| R is total path length in n steps r is the final position after n steps r o |r 1| |r 3| |r 2|

Papers: Microcellular systems, random walks and wave propagation. M. Franceschetti J. Bruck and L. Shulman Short version in Proceedings IEEE AP-S ’ 02. A pulse sounding thought experiment M. Franceschetti, David Tse In preparation Download from: WWW. . . edu/~massimo Or send email to: massimof@EECS. berkeley. edu