5e3f091242b5cfa3bbb1b6caf5bff8b2.ppt
- Количество слайдов: 108

The Travelling Salesman Problem: A brief survey Martin Grötschel Vorausschau auf die Vorlesung Das Travelling-Salesman-Problem (ADM III) im WS 2013/14 14. Oktober 2013 Martin Grötschel § Institute of Mathematics, Technische Universität Berlin (TUB) § DFG-Research Center “Mathematics for key technologies” (MATHEON) § Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB) groetschel@zib. de http: //www. zib. de/groetschel

2 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

3 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

4 Combinatorial optimization Given a finite set E and a subset I of the power set of E (the set of feasible solutions). Given, moreover, a value (cost, length, …) c(e) for all elements e of E. Find, among all sets in I, a set I such that its total value c(I) (= sum of the values of all elements in I) is as small (or as large) as possible. The parameters of a combinatorial optimization problem are: (E, I, c). An important issue: How is I given? Martin Grötschel

5 Special „simple“ combinatorial optimization problems Finding a § minimum spanning tree in a graph § shortest path in a directed graph § maximum matching in a graph § minimum capacity cut separating two given nodes of a graph or digraph § cost-minimal flow through a network with capacities and costs on all edges § … These problems are solvable in polynomial time. Martin Grötschel

6 Special „hard“ combinatorial optimization problems § travelling salesman problem (the prototype problem) § location und routing § set-packing, partitioning, -covering § max-cut § linear ordering § scheduling (with a few exceptions) § node and edge colouring §… These problems are NP-hard (in the sense of complexity theory). Martin Grötschel

7 The travelling salesman problem Given n „cities“ and „distances“ between them. Find a tour (roundtrip) through all cities visiting every city exactly once such that the sum of all distances travelled is as small as possible. (TSP) The TSP is called symmetric (STSP) if, for every pair of cities i and j, the distance from i to j is the same as the one from j to i, otherwise the problem is called asymmetric (ATSP). Martin Grötschel

http: //www. tsp. gatech. edu/

9 THE TSP book suggested reading for everyone interested in the TSP Martin Grötschel

10 Martin Grötschel Another recommendation Bill Cook‘s new book

11 The travelling salesman problem Two mathematical formulations of the TSP Martin Grötschel § Does that help solve the TSP?

12 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

13 Usually quoted as the forerunner of the TSP Usually quoted as the origin of the TSP Martin Grötschel

about 100 years earlier

15 By a proper choice and scheduling of the tour one can gain so much time that we have to make some suggestions The most important aspect is to cover as many locations as possible without visiting a location twice Martin Grötschel

16 A TSP contest 1962: 10. 000 $ Prize Martin Grötschel

17 Ulysses roundtrip (an even older TSP ? ) The paper „The Optimized Odyssey“ by Martin Grötschel and Manfred Padberg is downloadable from http: //www. zib. de/groetschel/pubnew/paper/groetschelpadberg 2001 a. pdf Martin Grötschel
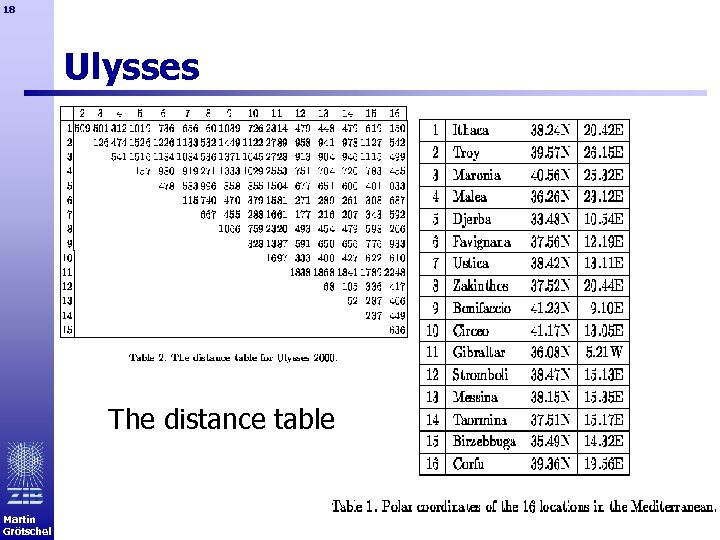
18 Ulysses The distance table Martin Grötschel
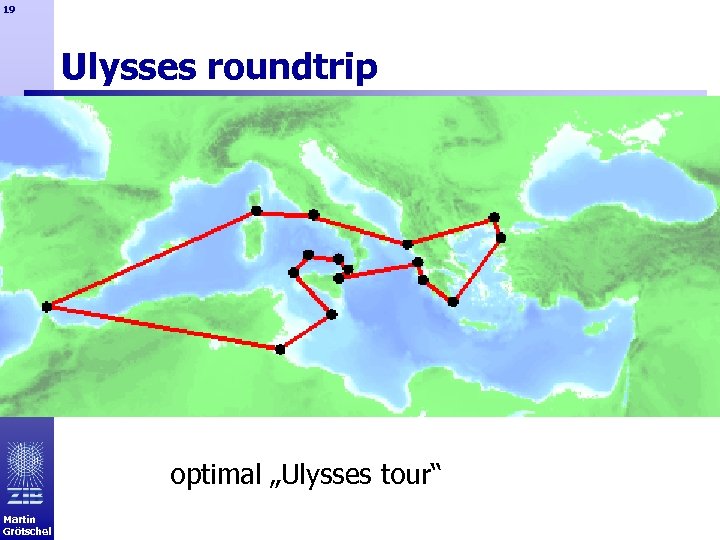
19 Ulysses roundtrip optimal „Ulysses tour“ Martin Grötschel

20 Malen nach Zahlen TSP in art ? § When was this invented? Martin Grötschel
21 Survey Books Literature: more than 1000 entries in Zentralblatt/Math Zbl 0562. 00014 Lawler, E. L. (ed. ); Lenstra, J. K. (ed. ); Rinnooy Kan, A. H. G. (ed. ); Shmoys, D. B. (ed. ) The traveling salesman problem. A guided tour of combinatorial optimization. Wiley-Interscience Series in Discrete Mathematics. A Wiley-Interscience publication. Chichester etc. : John Wiley & Sons. X, 465 p. (1985). MSC 2000: *00 Bxx 90 -06 Zbl 0996. 00026 Gutin, Gregory (ed. ); Punnen, Abraham P. (ed. ) The traveling salesman problem and its variations. Combinatorial Optimization. 12. Dordrecht: Kluwer Academic Publishers. xviii, 830 p. (2002). MSC 2000: *00 B 15 90 -06 90 Cxx Martin Grötschel

22 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

The Travelling Salesman Problem and Some of its Variants 23 The symmetric TSP The asymmetric TSP The TSP with precedences or time windows The online TSP The symmetric and asymmetric m-TSP The price collecting TSP The Chinese postman problem (undirected, mixed) § Bus, truck, vehicle routing § Edge/arc & node routing with capacities § Combinations of these and more § § § § Martin Grötschel

24 Martin Grötschel http: //www. densis. fee. unicamp. br/~ moscato/TSPBIB_home. html

25 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel
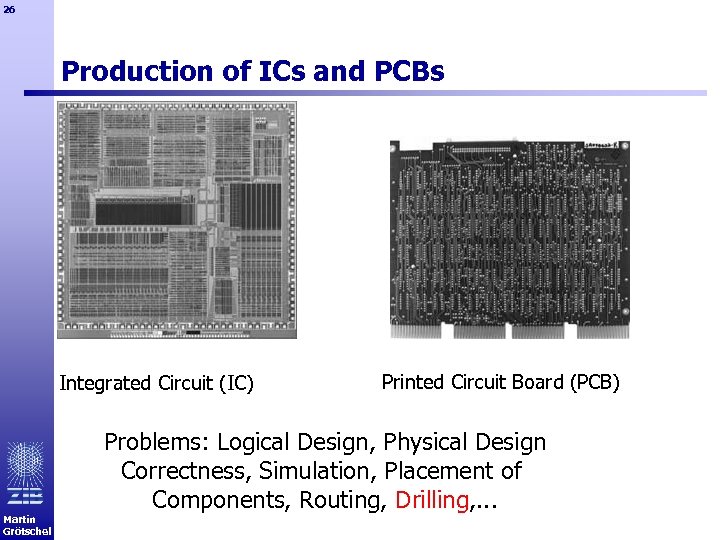
26 Production of ICs and PCBs Integrated Circuit (IC) Printed Circuit Board (PCB) Problems: Logical Design, Physical Design Correctness, Simulation, Placement of Components, Routing, Drilling, . . . Martin Grötschel

27 Correct modelling of a printed circuit board drilling problem length of a move of the drilling head: Euclidean norm, Max norm, Manhatten norm? 2103 holes to be drilled Martin Grötschel

28 Drilling 2103 holes into a PCB Significant Improvements via TSP (due to Padberg & Rinaldi) Martin Grötschel industry solution optimal solution

Siemens-Problem PCB da 4 Martin Grötschel, Michael Jünger, Gerhard Reinelt, Optimal Control of Plotting and Drilling Machines: A Case Study, Zeitschrift für Operations Research, 35: 1 (1991) 61 -84 http: //www. zib. de/groetschel/pubnew/paper/groetscheljuengerreinelt 1991. pdf before after

Siemens-Problem PCB da 1 Grötschel, Jünger, Reinelt before after
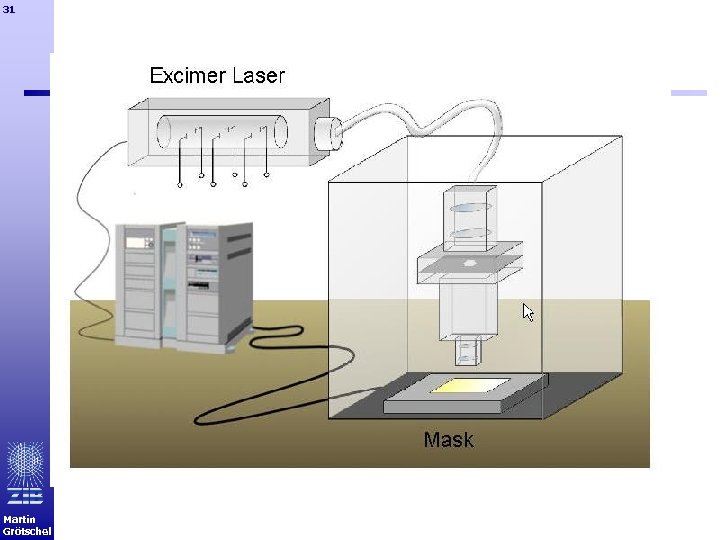
31 Martin Grötschel

32 Leiterplatten-Bohrmaschine Printed Circuit Board Drilling Machine Martin Grötschel

33 Martin Grötschel Foto einer Flachbaugruppe (Leiterplatte)

34 Martin Grötschel Foto einer Flachbaugruppe (Leiterplatte) - Rückseite

35 442 holes to be drilled Martin Grötschel

36 Typical PCB drilling problems at Siemens da 1 da 2 da 3 da 4 Number of holes 2457 423 2203 2104 Number of drills 7 7 6 10 3518728 1049956 1958161 4347902 Tour length Table 4 Martin Grötschel
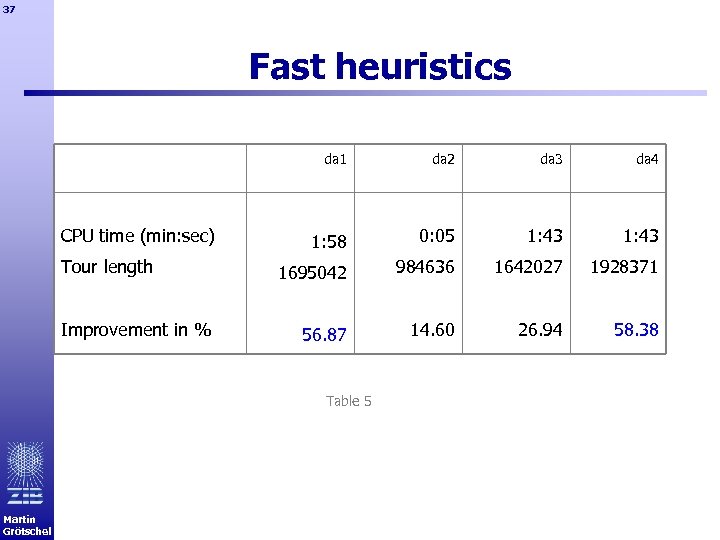
37 Fast heuristics da 1 CPU time (min: sec) Tour length Improvement in % da 2 da 3 da 4 1: 58 0: 05 1: 43 1695042 984636 1642027 1928371 56. 87 14. 60 26. 94 58. 38 Table 5 Martin Grötschel

38 Martin Grötschel Optimizing the stacker cranes of a Siemens-Nixdorf warehouse

39 Herlitz at Falkensee (Berlin) Martin Grötschel

40 Martin Grötschel Example: Control of the stacker cranes in a Herlitz warehouse
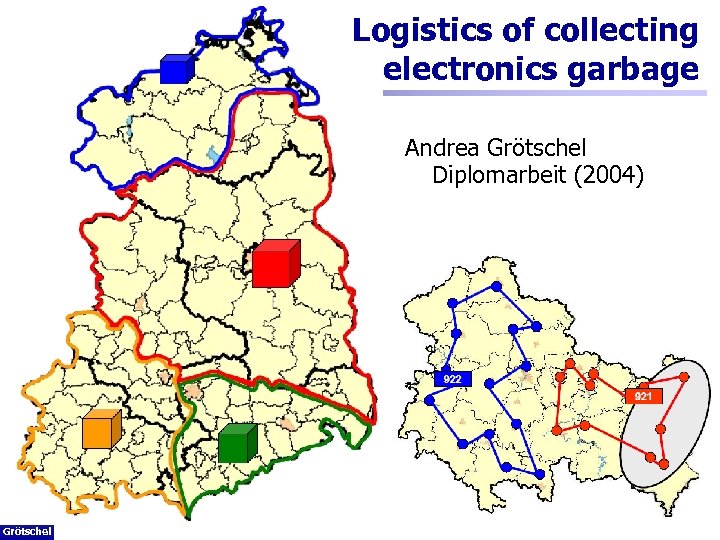
41 Logistics of collecting electronics garbage Andrea Grötschel Diplomarbeit (2004) Martin Grötschel

42 Location plus tour planning (m-TSP) Martin Grötschel

43 The Dispatching Problem at ADAC: an online m-TSP Dispatching Center (Pannenzentrale) Data Transm. „Gelber Engel“ Martin Grötschel Dispatcher
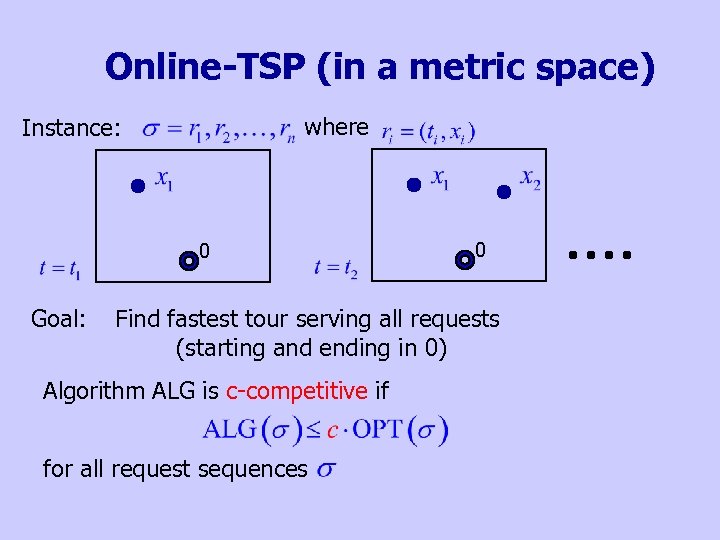
Online-TSP (in a metric space) where Instance: 0 Goal: 0 Find fastest tour serving all requests (starting and ending in 0) Algorithm ALG is c-competitive if for all request sequences

45 Implementation competitions Martin Grötschel

46 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

47 LP Cutting Plane Approach Even MODELLING is not easy! What is the „right“ LP relaxation? N. Ascheuer, M. Fischetti, M. Grötschel, „Solving the Asymmetric Travelling Salesman Problem with time windows by branch-and-cut“, Mathematical Programming A (2001), see http: //www. zib. de/groetschel/pubnew/paper/ascheuerfischettigroetschel 2001. pdf Martin Grötschel

48 IP formulation of the asymmetric TSP Martin Grötschel

49 Time Windows § This is a typical situation in delivery problems. § Customers must be served during a certain period of time, usually a time interval is given. § access to pedestrian areas § opening hours of a customer § delivery to assembly lines § just in time processes Martin Grötschel

50 Model 1 Martin Grötschel

51 Model 2 Martin Grötschel

52 Model 3 Martin Grötschel

Model 1, 2, 3

54 Cutting Planes Used for all Three Models (Separation Routines) § § § Martin Grötschel Subtour Elimination Constraints (SEC) 2 -Matching Constraints -Inequalities "Special“ Inequalities and PCB-Inequalities Dk-Inequalities Infeasible Path Elimination Constraints (IPEC) Strengthened -Inequalities Two-Job Cuts Pool Separation SD-Inequalities + various strengthenings/liftings

55 Further Implementation Details § Preprocessing § § Tightening Time Windows Release and Due Date Adjustment Construction of Precedences Elimination of Arcs Branching (only on x-variables) Enumeration Strategy (DFS, Best-FS) Pricing Frequency (every 5 th iteration) Tailing Off LP-exploitation Heuristics (after a new feasible LP solution is found), they outperform the other heuristics § § § Martin Grötschel

56 Results § Very uneven performance § Model 1 is really bad in general § Model 2 is best on the average (winner in 16 of 22 test cases) § Model 3 is better when few time windows are active (6 times winner, last in all other cases, severe numerical problems, very difficult LPs) Martin Grötschel How could you have guessed?
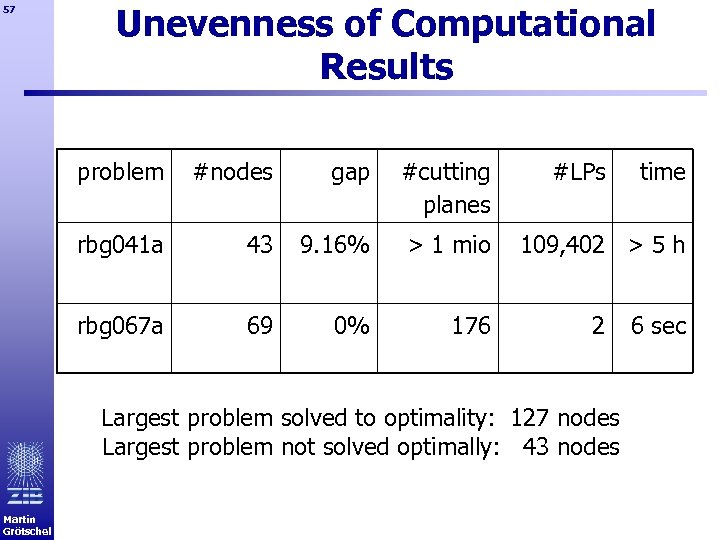
57 Unevenness of Computational Results problem #nodes gap #cutting planes rbg 041 a 43 9. 16% > 1 mio rbg 067 a 69 0% 176 #LPs 109, 402 > 5 h 2 Largest problem solved to optimality: 127 nodes Largest problem not solved optimally: 43 nodes Martin Grötschel time 6 sec

58 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

59 Need for Heuristics § Many real-world instances of hard combinatorial optimization problems are (still) too large for exact algorithms. § Or the time limit stipulated by the customer for the solution is too small. § Therefore, we need heuristics! § Exact algorithms usually also employ heuristics. § What is urgently needed is a decision guide: Which heuristic will most likely work well on what problem ? Martin Grötschel

60 Primal and Dual Heuristics § Primal Heuristic: Finds a (hopefully) good feasible solution. § Dual Heuristic: Finds a bound on the optimum solution value (e. g. , by finding a feasible solution of the LP-dual of an LPrelaxation of a combinatorial optimization problem). Minimization: dual heuristic value ≤ optimum value ≤ primal heuristic value quality guarantee in practice and theory Martin Grötschel

61 Heuristics: A Survey § Greedy Algorithms § Exchange & Insertion Algorithms § Neighborhood/Local Search § Variable Neighborhood Search, Iterated Local Search § Random sampling § Simulated Annealing § Taboo search § Great Deluge Algorithms § Simulated Tunneling § Neural Networks § Scatter Search Martin Grötschel § Greedy Randomized Adaptive Search Procedures

62 Heuristics: A Survey § Genetic, Evolutionary, and similar Methods § DNA-Technology § Ant and Swarm Systems § (Multi-) Agents § Population Heuristics § Memetic Algorithms (Meme are the “missing links” gens and mind) § Fuzzy Genetics-Based Machine Learning § Fast and Frugal Method (Psychology) § Method of Devine Intuition (Psychologist Thorndike) Martin Grötschel § …. .

63 The typical heuristics junk § Hyper-heuristics in Co-operative Search The interest in parallel co-operative approaches has risen considerably due to, not only the availability of co-operative environments at low cost, but also their success to provide novel ways to combine different (meta-)heuristics. Current research has shown that the parallel execution and co-operation of several (meta-)heuristics could improve the quality of the solutions that each of them would be able to find by itself working on a standalone basis. Moreover, parallel and distributed approaches can be used to provide more powerful and robust problem solving environments in a variety of problem domains. Hyper-heuristics, on the other hand, represent a set of search methodologies which are applicable to different problem domains. They aim to raise the level of generality, for example by choosing and/or generating new methodologies on demand during the search process. The goal of this study is to explore the cooperative search mechanisms within a hyper-heuristic framework. This exciting research area lies at the interface between operational research and computer science and involves understanding of (distributed) decision making mechanisms and learning, design, implementation and analysis of automated search methodologies. The application domains will be cross disciplinary. Martin Grötschel
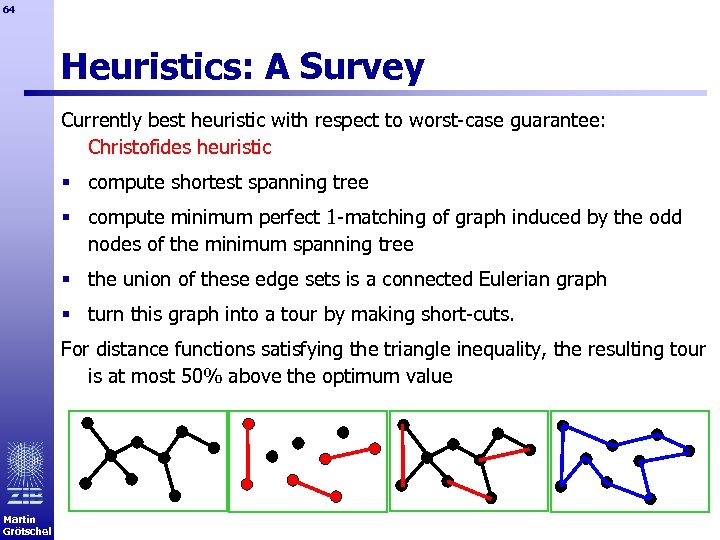
64 Heuristics: A Survey Currently best heuristic with respect to worst-case guarantee: Christofides heuristic § compute shortest spanning tree § compute minimum perfect 1 -matching of graph induced by the odd nodes of the minimum spanning tree § the union of these edge sets is a connected Eulerian graph § turn this graph into a tour by making short-cuts. For distance functions satisfying the triangle inequality, the resulting tour is at most 50% above the optimum value Martin Grötschel

65 Understanding Heuristics, Approximation Algorithms § worst case analysis § There is no polynomial time approx. algorithm for STSP/ATSP. § Christofides algorithm for the STSP with triangle inequality § average case analysis § Karp‘s analysis of the patching algorithm for the ATSP § probabilistic problem analysis § for Euclidean STSP in unit square, TSP constant 1. 714. . § polynomial time approximation schemes (PAS) § Arora‘s polynomial-time approximation schemes for Euclidean STSPs § fully-polynomial time approximation schemes (FPAS) § not for TSP/ATSP but, e. g. , for knapsack (Ibarra&Kim) § These concepts – unfortunately – often do not really help to guide practice. § experimental evaluation § Lin-Kernighan for STSP (DIMACS challenges)) Martin Grötschel

66 Contents 1. Introduction 2. The TSP and some of its history 3. The TSP and some of its variants 4. Some applications 5. Modeling issues 6. Heuristics 7. How combinatorial optimizers do it Martin Grötschel

67 Polyhedral Theory (of the TSP) STSP-, ATSP-, TSP-with-side-constraints- Polytope: = Convex hull of all incidence vectors of feasible tours To be investigated: § Dimension § Equation system defining the affine hull § Facets § Separation algorithms Martin Grötschel

68 The symmetric travelling salesman polytope § The LP relaxation is solvable in polynomial time Martin Grötschel

69 Relation between IP and LP-relaxation Open Problem: § If costs satisfy the triangle inequality, then IP-OPT <= 4/3 LP-SEC IP-OPT <= 3/2 LP-SEC (Wolsey) Martin Grötschel

70 General cutting plane theory: Gomory Mixed-Integer Cut § Given and § Rounding: Where define § Then § Disjunction: § Combining Martin Grötschel

71 clique trees § A clique tree is a connected graph C=(V, E), composed of cliques satisfying the following properties Martin Grötschel
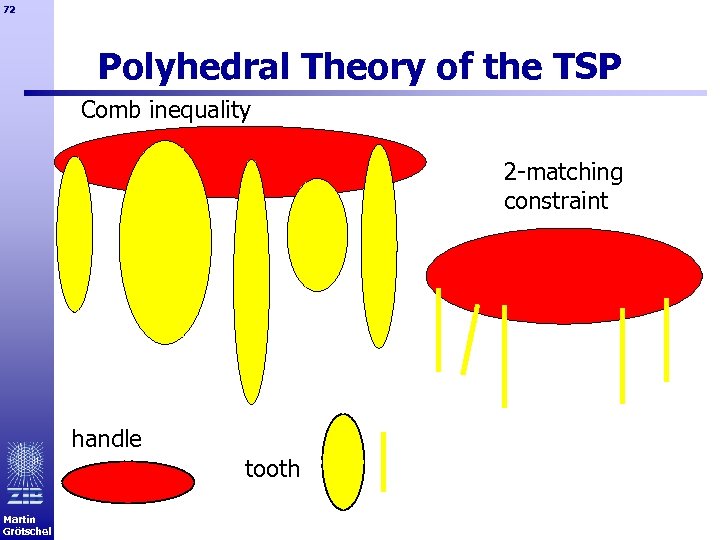
72 Polyhedral Theory of the TSP Comb inequality 2 -matching constraint handle tooth Martin Grötschel
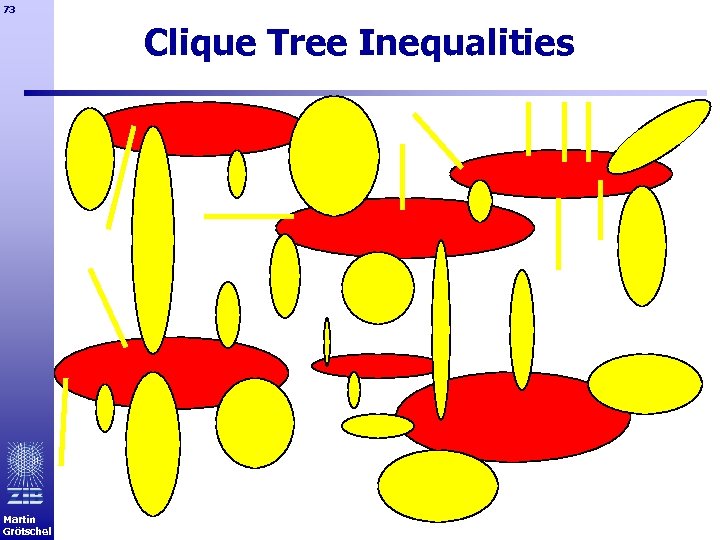
73 Clique Tree Inequalities Martin Grötschel
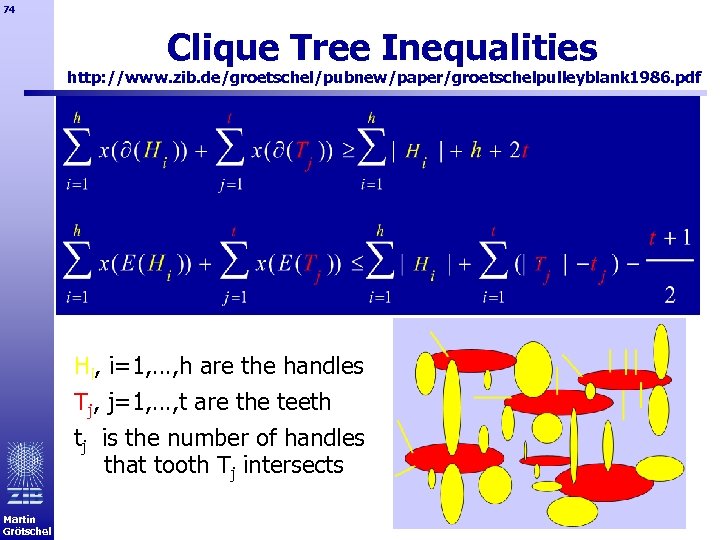
74 Clique Tree Inequalities http: //www. zib. de/groetschel/pubnew/paper/groetschelpulleyblank 1986. pdf Hi, i=1, …, h are the handles Tj, j=1, …, t are the teeth tj is the number of handles that tooth Tj intersects Martin Grötschel

75 Valid Inequalities for STSP § § § Martin Grötschel Trivial inequalities Degree constraints Subtour elimination constraints 2 -matching constraints, comb inequalities Clique tree inequalities (comb) Bipartition inequalities (clique tree) Path inequalities (comb) Star inequalities (path) Binested Inequalities (star, clique tree) Ladder inequalities (2 handles, even # of teeth) Domino inequalities Hypohamiltonian, hypotraceable inequalities § etc.
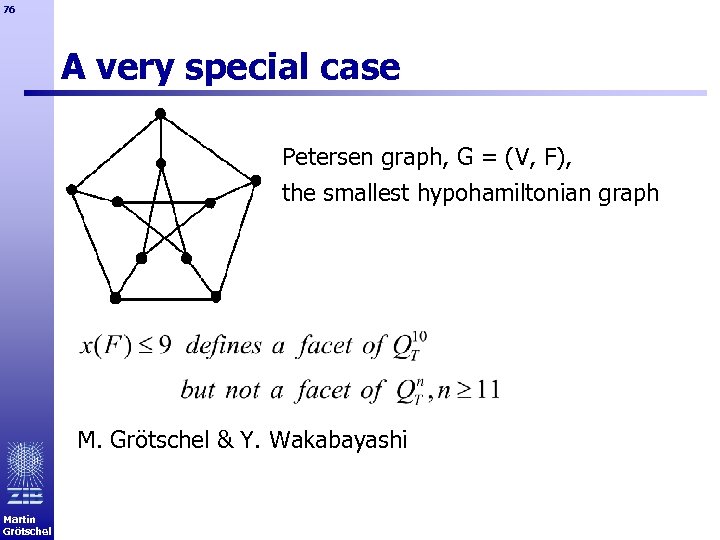
76 A very special case Petersen graph, G = (V, F), the smallest hypohamiltonian graph M. Grötschel & Y. Wakabayashi Martin Grötschel
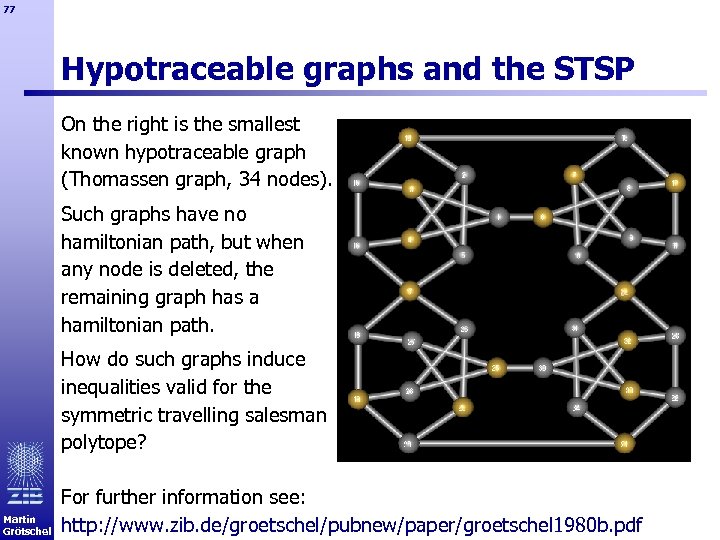
77 Hypotraceable graphs and the STSP On the right is the smallest known hypotraceable graph (Thomassen graph, 34 nodes). Such graphs have no hamiltonian path, but when any node is deleted, the remaining graph has a hamiltonian path. How do such graphs induce inequalities valid for the symmetric travelling salesman polytope? Martin Grötschel For further information see: http: //www. zib. de/groetschel/pubnew/paper/groetschel 1980 b. pdf

78 “Wild facets of the asymmetric travelling salesman polytope” § Hypohamiltonian and hypotraceable directed graphs also exist and induce facets of the polytopes associated with the asymmetric TSP. § Information “hypohamiltonian” and “hypotraceable” inequalities can be found in http: //www. zib. de/groetschel/pubnew/paper/groetschelwakabayashi 1981 a. pdf http: //www. zib. de/groetschel/pubnew/paper/groetschelwakabayashi 1981 b. pdf Martin Grötschel

79 Valid and facet defining inequalities for STSP: Survey articles § M. Grötschel, M. W. Padberg (1985 a, b) § M. Jünger, G. Reinelt, G. Rinaldi (1995) § D. Naddef (2002) § The TSP book (ABCC, 2006) Martin Grötschel
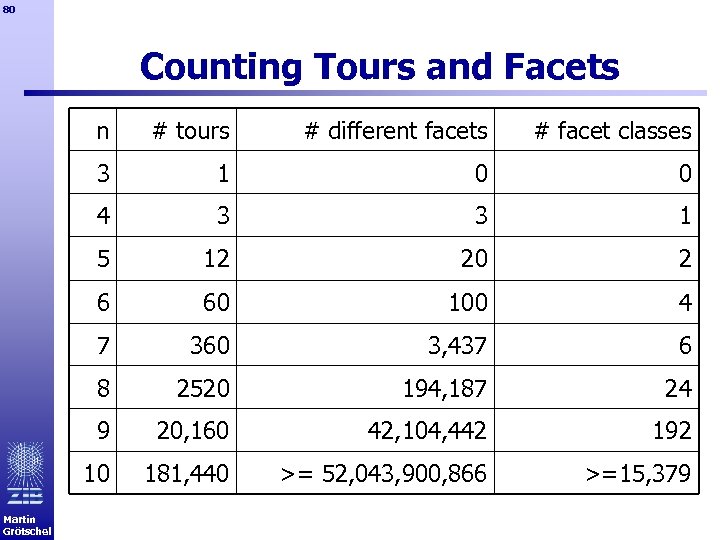
80 Counting Tours and Facets n # different facets # facet classes 3 1 0 0 4 3 3 1 5 12 20 2 6 60 100 4 7 360 3, 437 6 8 2520 194, 187 24 9 20, 160 42, 104, 442 192 10 Martin Grötschel # tours 181, 440 >= 52, 043, 900, 866 >=15, 379

81 Separation Algorithms § Given a system of valid inequalities (possibly of exponential size). § Is there a polynomial time algorithm (or a good heuristic) that, § given a point, § checks whether the point satisfies all inequalities of the system, and § if not, finds an inequality violated by the given point? Martin Grötschel
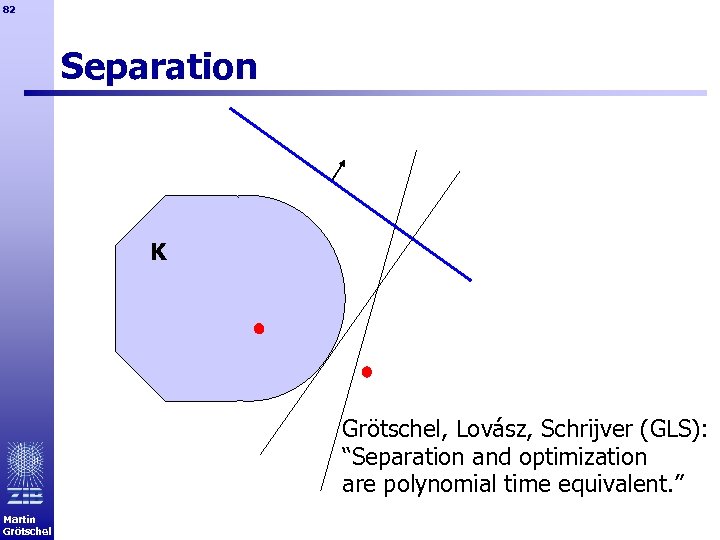
82 Separation K Grötschel, Lovász, Schrijver (GLS): “Separation and optimization are polynomial time equivalent. ” Martin Grötschel

83 Separation Algorithms § There has been great success in finding exact polynomial time separation algorithms, e. g. , § for subtour-elimination constraints § for 2 -matching constraints (Padberg&Rao, 1982) § or fast heuristic separation algorithms, e. g. , § for comb constraints § for clique tree inequalities § and these algorithms are practically efficient Martin Grötschel

84 Polyhedral Combinatorics § This line of research has resulted in powerful cutting plane algorithms for combinatorial optimization problems. § They are used in practice to solve exactly or approximately (including branch & bound) large-scale real-world instances. Martin Grötschel
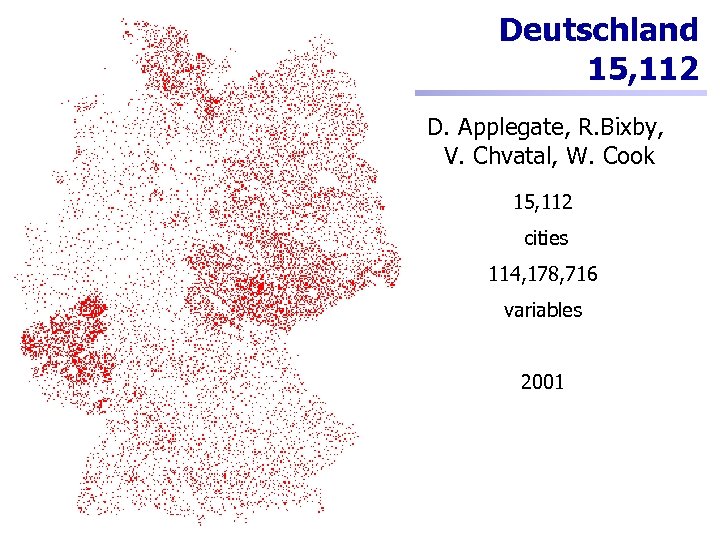
85 Deutschland 15, 112 D. Applegate, R. Bixby, V. Chvatal, W. Cook 15, 112 cities 114, 178, 716 variables 2001 Martin Grötschel

86 How do we solve a TSP like this? § Upper bound: Heuristic search § Chained Lin-Kernighan § Lower bound: § Linear programming § Divide-and-conquer § Polyhedral combinatorics § Parallel computation § Algorithms & data structures The LOWER BOUND is the mathematically and algorithmically hard part of the work Martin Grötschel

87 Work on LP relaxations of the symmetric travelling salesman polytope § Integer Programming Approach Martin Grötschel
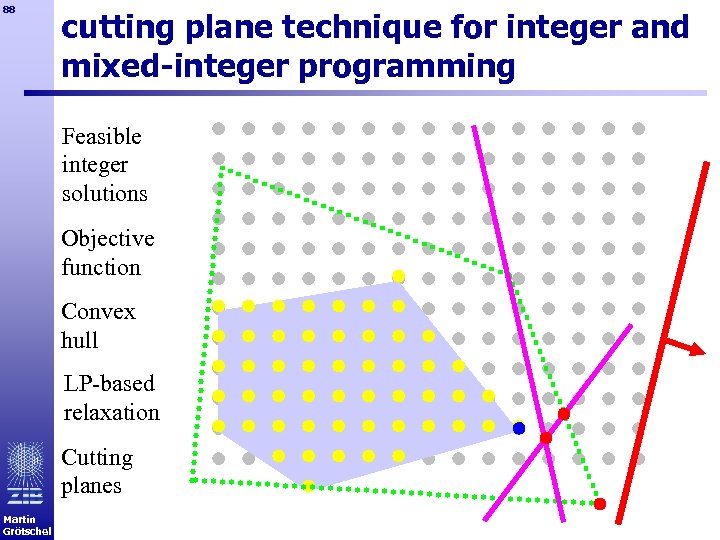
88 cutting plane technique for integer and mixed-integer programming Feasible integer solutions Objective function Convex hull LP-based relaxation Cutting planes Martin Grötschel
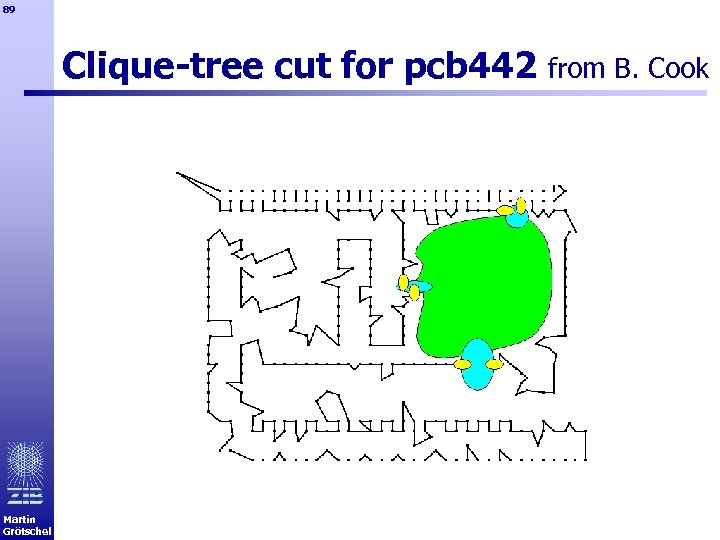
89 Clique-tree cut for pcb 442 Martin Grötschel from B. Cook
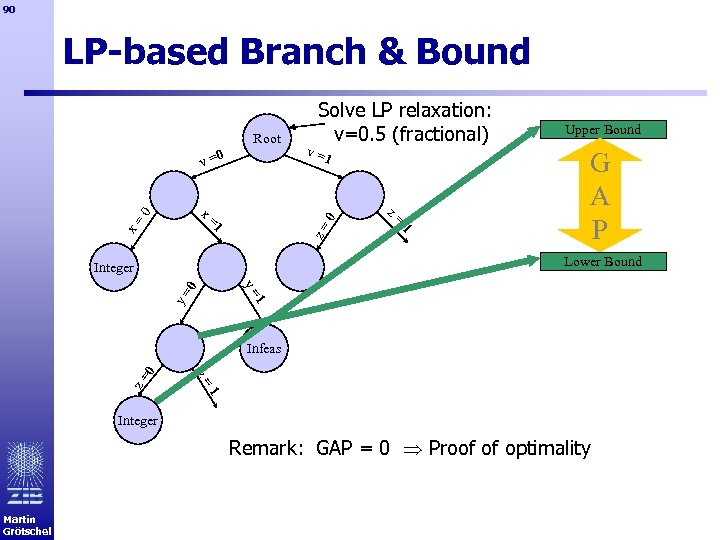
90 LP-based Branch & Bound Root v =0 0 z= 0 x= 1 =1 v =1 z= x Solve LP relaxation: v=0. 5 (fractional) Upper Bound G A P Lower Bound Integer 1 y= 0 y= z= z= 0 Infeas 1 Integer Remark: GAP = 0 Proof of optimality Martin Grötschel
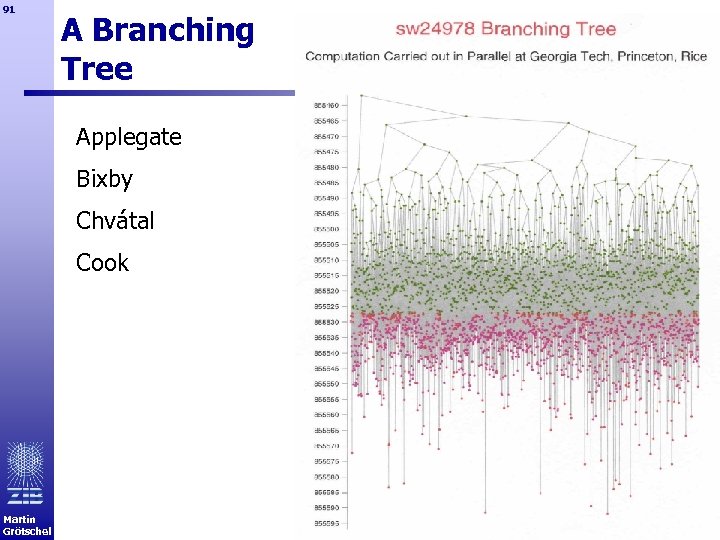
91 A Branching Tree Applegate Bixby Chvátal Cook Martin Grötschel
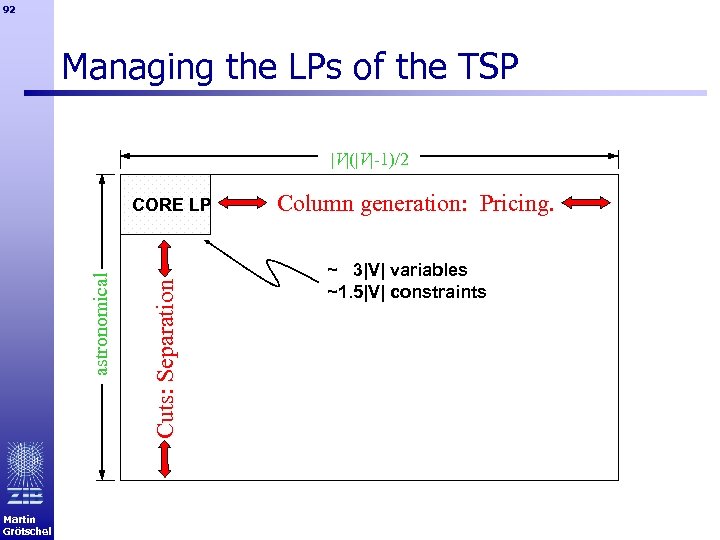
92 Managing the LPs of the TSP |V|(|V|-1)/2 Martin Grötschel Cuts: Separation astronomical CORE LP Column generation: Pricing. ~ 3|V| variables ~1. 5|V| constraints

93 Martin Grötschel A Pictorial History of Some TSP World Records
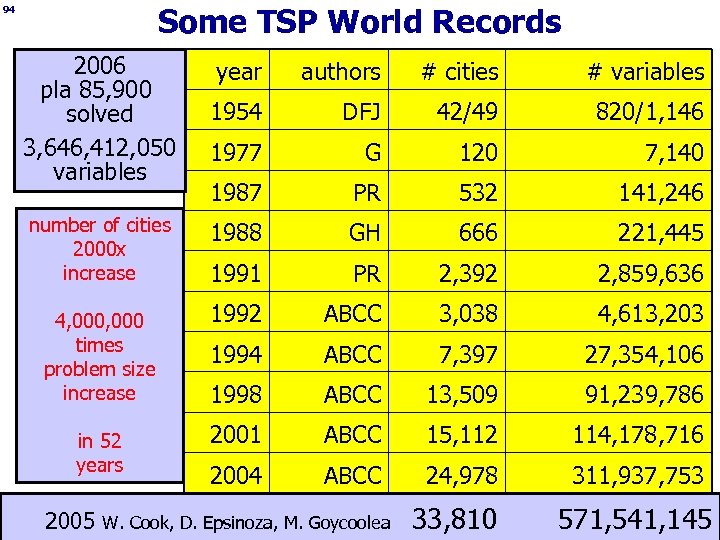
Some TSP World Records 94 2006 pla 85, 900 solved 3, 646, 412, 050 variables year authors # cities # variables 1954 DFJ 42/49 820/1, 146 1977 G 120 7, 140 1987 PR 532 141, 246 number of cities 2000 x increase 1988 GH 666 221, 445 1991 PR 2, 392 2, 859, 636 4, 000 times problem size increase 1992 ABCC 3, 038 4, 613, 203 1994 ABCC 7, 397 27, 354, 106 1998 ABCC 13, 509 91, 239, 786 in 52 years 2001 ABCC 15, 112 114, 178, 716 2004 ABCC 24, 978 311, 937, 753 2005 W. Cook, D. Epsinoza, M. Goycoolea 33, 810 571, 541, 145 Martin Grötschel

95 The current champions ABCC stands for D. Applegate, B. Bixby, W. Cook, V. Chvátal § almost 15 years of code development § presentation at ICM’ 98 in Berlin, see proceedings § have made their code CONCORDE available in the Internet Martin Grötschel
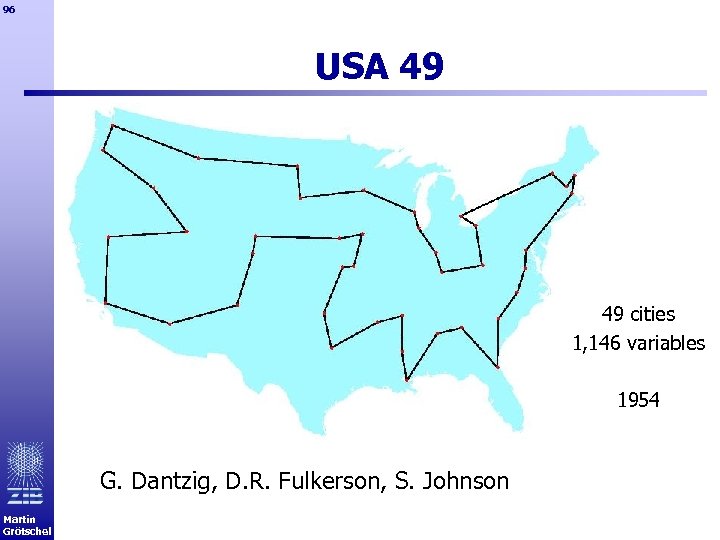
96 USA 49 49 cities 1, 146 variables 1954 G. Dantzig, D. R. Fulkerson, S. Johnson Martin Grötschel
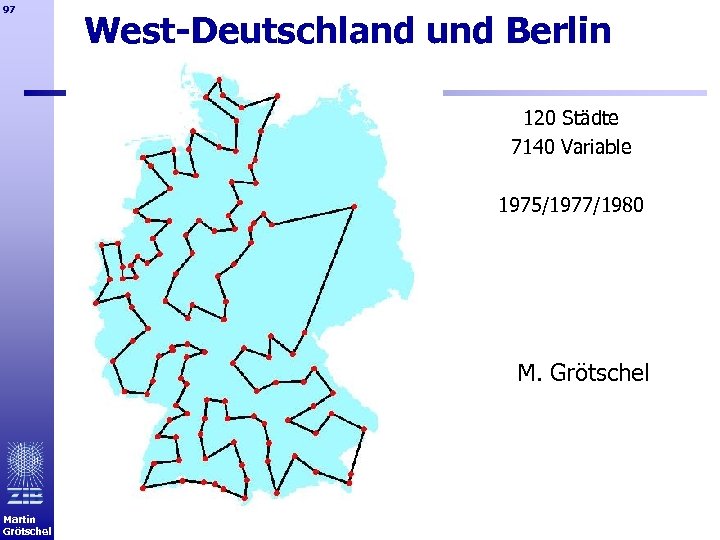
97 West-Deutschland und Berlin 120 Städte 7140 Variable 1975/1977/1980 M. Grötschel Martin Grötschel
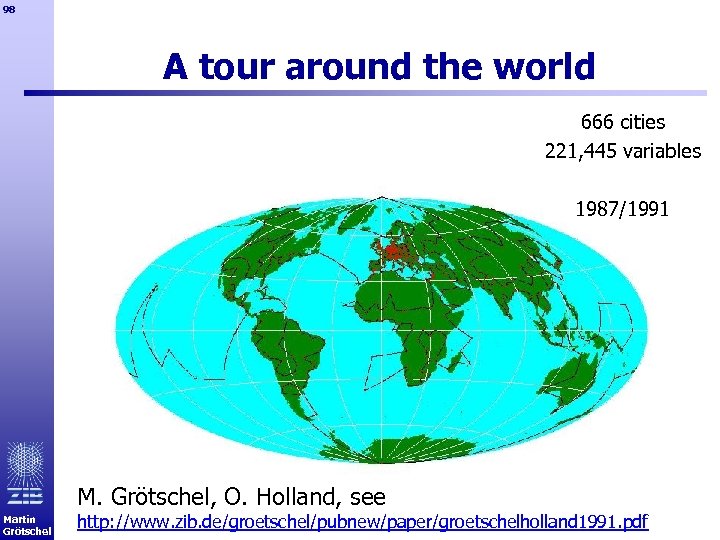
98 A tour around the world 666 cities 221, 445 variables 1987/1991 M. Grötschel, O. Holland, see Martin Grötschel http: //www. zib. de/groetschel/pubnew/paper/groetschelholland 1991. pdf
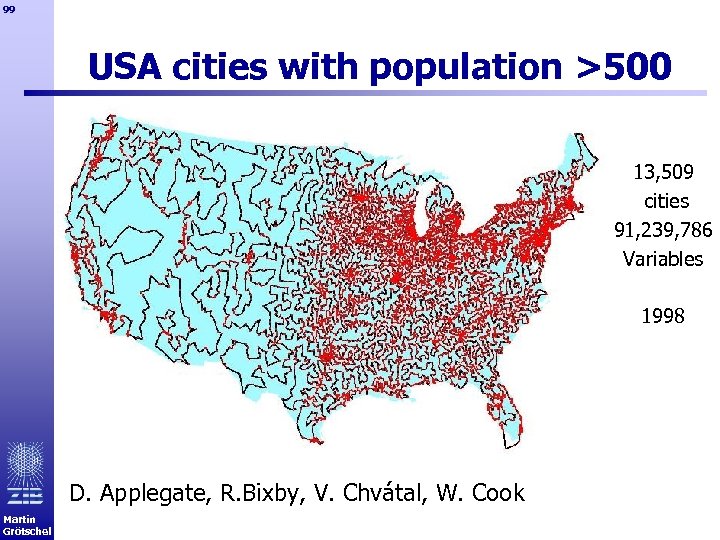
99 USA cities with population >500 13, 509 cities 91, 239, 786 Variables 1998 D. Applegate, R. Bixby, V. Chvátal, W. Cook Martin Grötschel
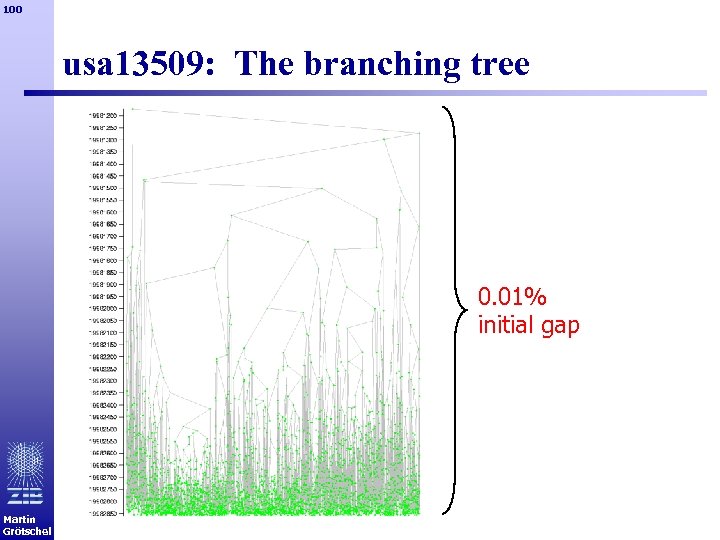
100 usa 13509: The branching tree 0. 01% initial gap Martin Grötschel

101 Summary: usa 13509 § 9539 nodes branching tree § 48 workstations (Digital Alphas, Intel Pentium IIs, Pentium Pros, Sun Untra. Sparcs) § Total CPU time: 4 Martin Grötschel cpu years
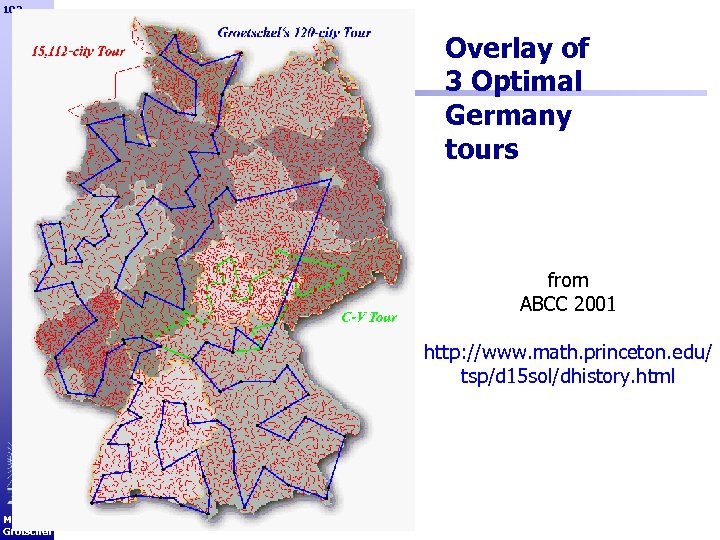
102 Overlay of 3 Optimal Germany tours from ABCC 2001 http: //www. math. princeton. edu/ tsp/d 15 sol/dhistory. html Martin Grötschel
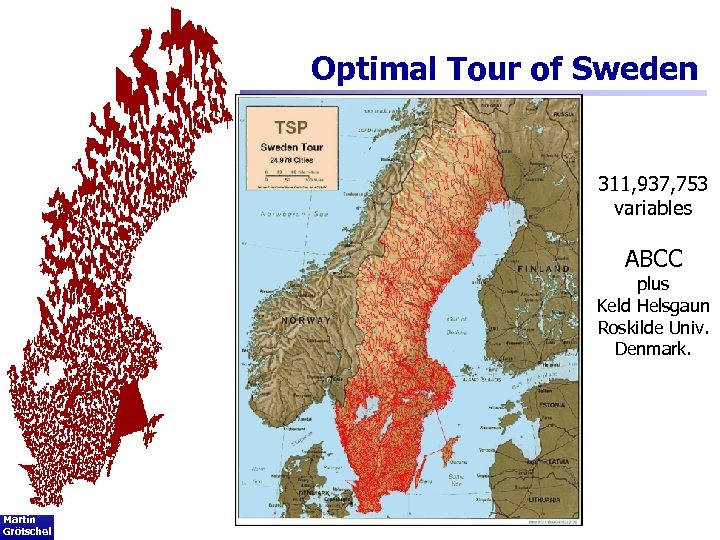
103 Optimal Tour of Sweden 311, 937, 753 variables ABCC plus Keld Helsgaun Roskilde Univ. Denmark. Martin Grötschel
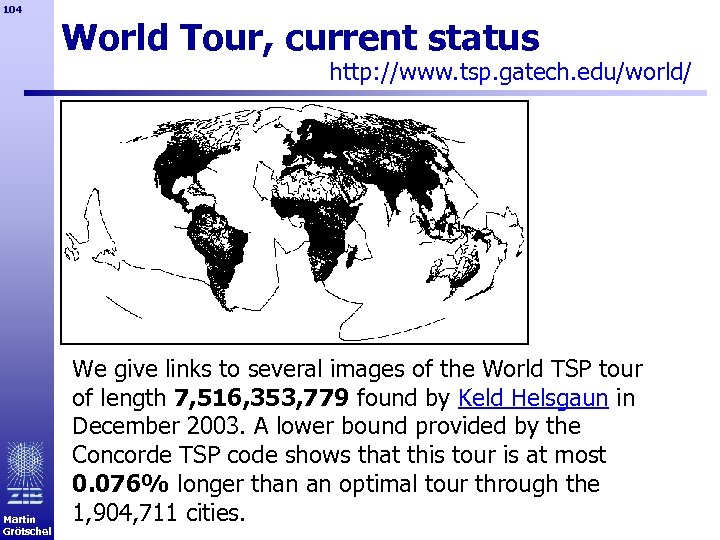
104 World Tour, current status http: //www. tsp. gatech. edu/world/ Martin Grötschel We give links to several images of the World TSP tour of length 7, 516, 353, 779 found by Keld Helsgaun in December 2003. A lower bound provided by the Concorde TSP code shows that this tour is at most 0. 076% longer than an optimal tour through the 1, 904, 711 cities.

105 Vorlesungsplan § Kapitel 1. Das Travelling-Salesman- und verwandte Probleme: ein Überblick und Anwendungen § 1. Vorlesung: ppt-Überblick über das TSP, alte Folien und Cook. Book, Archäologie, Dantzig, Fulkerson und Johnson § Kapitel 2. Hamiltonsche und hypohamiltonsche Graphen und Digraphen § 2. Vorlesung: Hamiltonsche Graphen aus Bondy und Murty § 3. Vorlesung: Hypohamiltonsche und Hypobegehbare Graphen (Thomassen-Paper und Paper mit Yoshiko) § Kapitel 3. Die „natürlichen“ IP-Formulierungen des TSP und des ATSP, Travelling Salesman-Polytope Subtour-Formulierungen, STSP und ATSP-Polytop Martin Grötschel § Kapitel 4. Kombinatorische Verwandte des TSP Das 1 -Baum-, 2 -Matching-, Zuordnungs-, 1 -Arboreszenz-Problem

106 Vorlesungsplan § Kapitel 5. Gütegarantien für Heuristiken, Eröffnungsheuristiken für das TSP (NN, Insert, Christofides, . . . ) § Kapitel 6. Verbesserungsheuristiken und ein polynomiales Approximationsschema (Exchange, LK, Helsgaun, Simulated Annealing, evolutionäre Algorithmen, . . . ) § Kapitel 7. Ein Branch&Bound-Verfahren für das ATSP Assignment-B&B § Kapitel 8. 1 -Bäume, Lagrange-Relaxierung und untere Schranken durch ein Subgradientenverfahren (Held&Karp) § Kapitel 9. Alternative IP-Modelle § Kapitel 10. Das symmetrische TSP-Polytop § Kapitel 11. Schnittebenenerkennung/Separationsalgorithmen Martin Grötschel

107 Vorlesungsplan § Kapitel 12. Zur praktischen Lösung großer TSPs § Kapitel 13. TSPs mit Nebenbedingungen (Reihenfolgebedingungen, Zeitfenster, Multi-Salesmen, . . . ) § Unterwegs einbauen: Malen nach Zahlen, TSP-Portraits (Gesichter), Knights-Problem im Schach, Routenplanung, . . . Martin Grötschel

The Travelling Salesman Problem a brief survey Martin Grötschel Vorausschau auf die Vorlesung Das Travelling-Salesman-Problem (ADM III) The END 14. Oktober 2013 Martin Grötschel § Institute of Mathematics, Technische Universität Berlin (TUB) § DFG-Research Center “Mathematics for key technologies” (MATHEON) § Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB) groetschel@zib. de http: //www. zib. de/groetschel
5e3f091242b5cfa3bbb1b6caf5bff8b2.ppt