THE TIME VALUE OF MONEY Lecture 4
Key Concepts and Skills • Be able to compute the future value of an investment made today • Be able to compute the present value of cash to be received at some future date • Be able to compute the return on an investment • Be able to compute the number of periods that equates a present value and a future value given an interest rate • Be able to use a financial calculator and a spreadsheet to solve time value of money problems
Time Value of Money q. Money has a time value because it can earn more money over time (earning power). q. Money has a time value because its purchasing power changes over time (inflation). q. Time value of money is measured in terms of interest rate. q. Interest is the cost of money—a cost to the borrower and an earning to the lender
What is Time Value? • We say that money has a time value because that money can be invested with the expectation of earning a positive rate of return • In other words, “a dollar received today is worth more than a dollar to be received tomorrow” • That is because today’s dollar can be invested so that we have more than one dollar tomorrow
Methods of Calculating Interest n n Simple interest: the practice of charging an interest rate only to an initial sum (principal amount). Compound interest: the practice of charging an interest rate to an initial sum and to any previously accumulated interest that has not been withdrawn.
The Terminology of Time Value • Present Value - An amount of money today, or the current value of a future cash flow • Future Value - An amount of money at some future time period • Period - A length of time (often a year, but can be a month, week, day, hour, etc. ) • Interest Rate - The compensation paid to a lender (or saver) for the use of funds expressed as a percentage for a period (normally expressed as an annual rate)
Abbreviations PV - Present value FV - Future value Pmt - Per period payment amount N - Either the total number of cash flows or the number of a specific period i - The interest rate period
Simple Interest Example: PV = $1, 000 i = 8% N = 3 years End of Year Beginning Balance Interest earned 0 Ending Balance $1, 000 1 $1, 000 $80 $1, 080 2 $1, 080 $1, 160 3 $1, 160 $80 $1, 240
Compound Interest Compound interest: the practice of charging an interest rate to an initial sum and to any previously accumulated interest that has not been withdrawn.
Compound Interest Example: PV= $1, 000 i = 8% N = 3 years End of Year Beginning Balance Interest earned 0 Ending Balance $1, 000 1 $1, 000 $80 $1, 080 2 $1, 080 $86. 40 $1, 166. 40 3 $1, 166. 40 $93. 31 $1, 259. 71
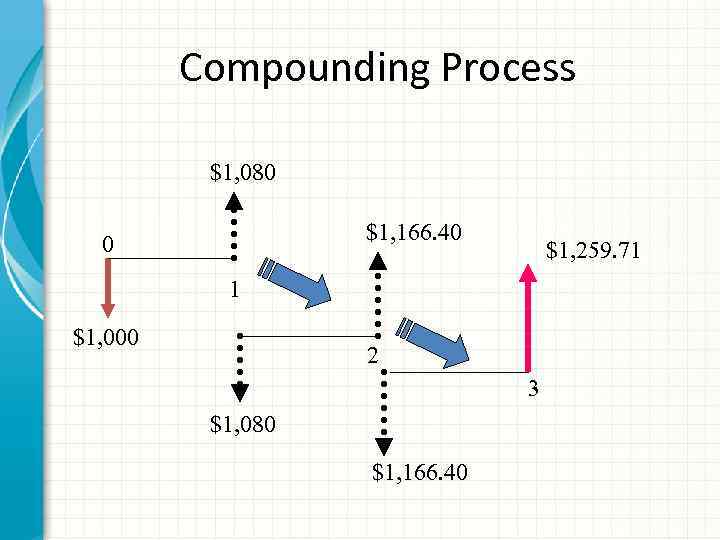Compounding Process $1, 080 $1, 166. 40 0 $1, 259. 71 1 $1, 000 2 3 $1, 080 $1, 166. 40
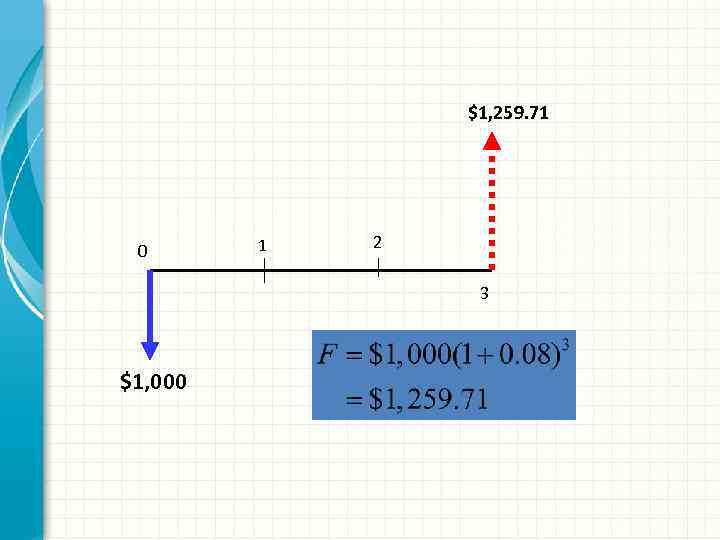$1, 259. 71 0 1 2 3 $1, 000
Compound Interest Formula
Some Fundamental Laws The Fundamental Law of Engineering Economy
Compound Interest “The greatest mathematical discovery of all time” Albert Einstein
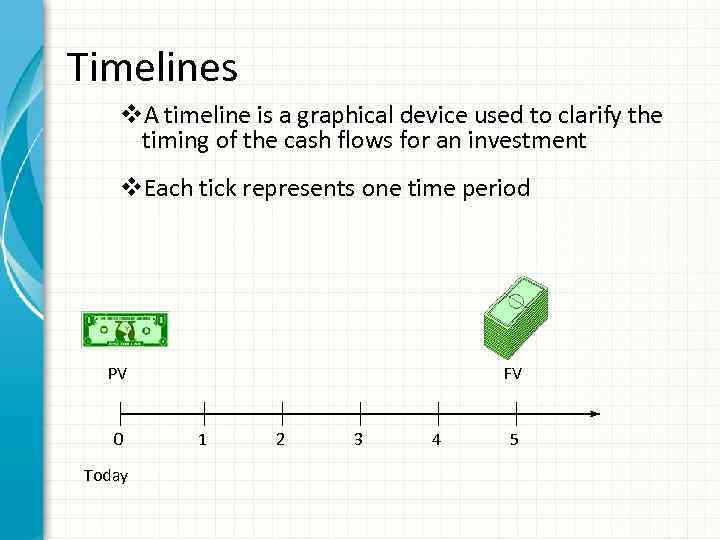Timelines v. A timeline is a graphical device used to clarify the timing of the cash flows for an investment v. Each tick represents one time period PV 0 Today FV 1 2 3 4 5
Calculating the Future Value • Suppose that you have an extra $100 today that you wish to invest for one year. If you can earn 10% per year on your investment, how much will you have in one year? -100 0 ? 1 2 3 4 5
Calculating the Future Value (cont. ) • Suppose that at the end of year 1 you decide to extend the investment for a second year. How much will you have accumulated at the end of year 2? -110 0 1 ? 2 3 4 5
Generalizing the Future Value • Recognizing the pattern that is developing, we can generalize the future value calculations as follows: v If you extended the investment for a third year, you would have:
Future Values: General Formula FV = PV(1 + i)N – – FV = future value PV = present value i = period interest rate, expressed as a decimal N = number of periods Future value interest factor = (1 + i)N
Compound Interest • Note from the example that the future value is increasing at an increasing rate • In other words, the amount of interest earned each year is increasing – Year 1: $10 – Year 2: $11 – Year 3: $12. 10 • The reason for the increase is that each year you are earning interest on the interest that was earned in previous years in addition to the interest on the original principle amount
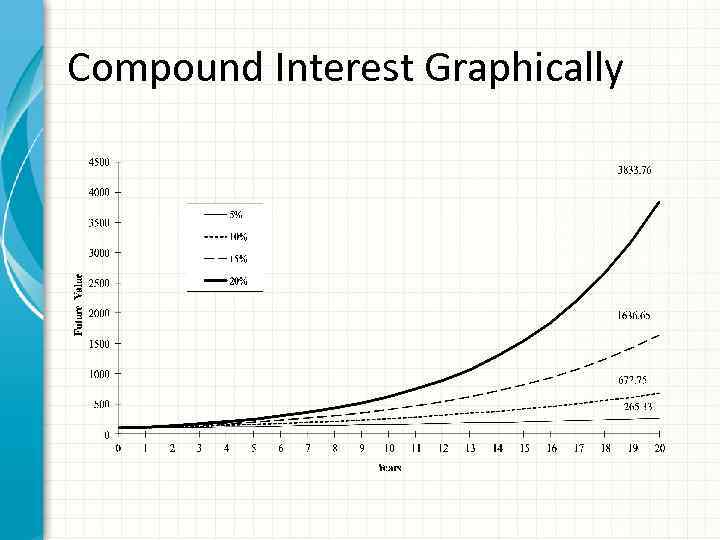Compound Interest Graphically
The Magic of Compounding • On Nov. 25, 1626 Peter Minuit, a Dutchman, reportedly purchased Manhattan from the Indians for $24 worth of beads and other trinkets. Was this a good deal for the Indians? • This happened about 371 years ago, so if they could earn 5% per year they would now (in 1997) have: v If they could have earned 10% per year, they would now have: That’s about 54, 563 Trillion dollars!
Future Values – Example 1 • Suppose you had a relative deposit $10 at 5. 5% interest 200 years ago. How much would the investment be worth today? • What is the effect of compounding? FV = 10(1. 055) = 10(44, 718. 9838) = 447, 189. 84 200 5 C-25
Calculating the Present Value • So far, we have seen how to calculate the future value of an investment • But we can turn this around to find the amount that needs to be invested to achieve some desired future value:
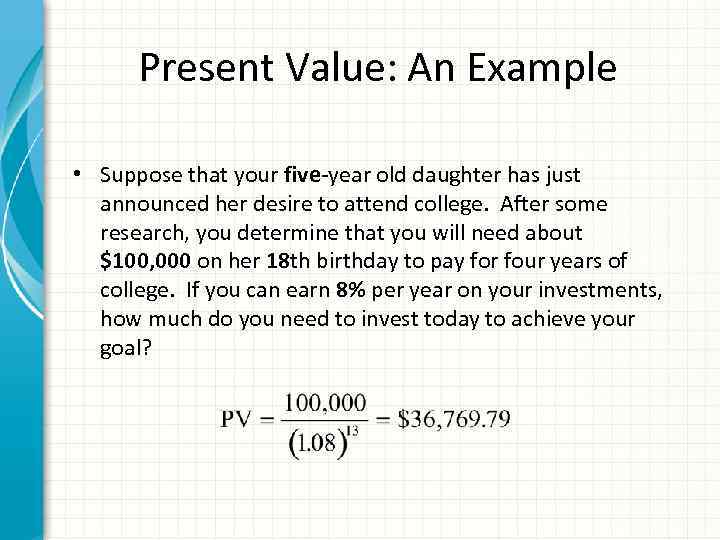Present Value: An Example • Suppose that your five-year old daughter has just announced her desire to attend college. After some research, you determine that you will need about $100, 000 on her 18 th birthday to pay for four years of college. If you can earn 8% per year on your investments, how much do you need to invest today to achieve your goal?
Annuities • An annuity is a series of nominally equal payments equally spaced in time • Annuities are very common: – – Rent Mortgage payments Car payment Pension income • The timeline shows an example of a 5 -year, $100 annuity 100 0 100 100 1 2 3 4 5
The Principle of Value Additivity • How do we find the value (PV or FV) of an annuity? • First, you must understand the principle of value additivity: – The value of any stream of cash flows is equal to the sum of the values of the components • In other words, if we can move the cash flows to the same time period we can simply add them all together to get the total value
Present Value of an Annuity • We can use the principle of value additivity to find the present value of an annuity, by simply summing the present values of each of the components:
Present Value of an Annuity (cont. ) • Using the example, and assuming a discount rate of 10% per year, we find that the present value is: 62. 09 68. 30 75. 13 82. 64 90. 91 100 379. 08 0 100 100 1 2 3 4 5
Present Value of an Annuity (cont. ) • Actually, there is no need to take the present value of each cash flow separately • We can use a closed-form of the PVA equation instead:
Present Value of an Annuity (cont. ) • We can use this equation to find the present value of our example annuity as follows: v This equation works for all regular annuities, regardless of the number of payments
The Future Value of an Annuity • We can also use the principle of value additivity to find the future value of an annuity, by simply summing the future values of each of the components:
The Future Value of an Annuity (cont. ) • Using the example, and assuming a discount rate of 10% per year, we find that the future value is: 146. 41 133. 10 121. 00 110. 00 100 100 100 1 2 3 4 5 } = 610. 51 at year 5
The Future Value of an Annuity (cont. ) • Just as we did for the PVA equation, we could instead use a closed-form of the FVA equation: v This equation works for all regular annuities, regardless of the number of payments
The Future Value of an Annuity (cont. ) • We can use this equation to find the future value of the example annuity:
Annuities Due • Thus far, the annuities that we have looked at begin their payments at the end of period 1; these are referred to as regular annuities • A annuity due is the same as a regular annuity, except that its cash flows occur at the beginning of the period rather than at the end 5 -period Annuity Due 5 -period Regular Annuity 100 0 100 100 100 1 2 3 4 5
Present Value of an Annuity Due • We can find the present value of an annuity due in the same way as we did for a regular annuity, with one exception • Note from the timeline that, if we ignore the first cash flow, the annuity due looks just like a four-period regular annuity • Therefore, we can value an annuity due with:
Present Value of an Annuity Due (cont. ) • Therefore, the present value of our example annuity due is: v Note that this is higher than the PV of the, otherwise equivalent, regular annuity
Future Value of an Annuity Due • To calculate the FV of an annuity due, we can treat it as regular annuity, and then take it one more period forward: Pmt Pmt Pmt 0 1 2 3 4 5
Future Value of an Annuity Due (cont. ) • The future value of our example annuity is: v Note that this is higher than the future value of the, otherwise equivalent, regular annuity
Deferred Annuities • A deferred annuity is the same as any other annuity, except that its payments do not begin until some later period • The timeline shows a five-period deferred annuity 100 0 1 2 100 100 3 4 5 6 7
PV of a Deferred Annuity • We can find the present value of a deferred annuity in the same way as any other annuity, with an extra step required • Before we can do this however, there is an important rule to understand: When using the PVA equation, the resulting PV is always one period before the first payment occurs
PV of a Deferred Annuity (cont. ) • To find the PV of a deferred annuity, we first find use the PVA equation, and then discount that result back to period 0 • Here we are using a 10% discount rate PV 2 = 379. 08 PV 0 = 313. 29 0 0 0 100 100 100 1 2 3 4 5 6 7
PV of a Deferred Annuity (cont. ) Step 1: Step 2:
FV of a Deferred Annuity • The future value of a deferred annuity is calculated in exactly the same way as any other annuity • There are no extra steps at all
Uneven Cash Flows • Very often an investment offers a stream of cash flows which are not either a lump sum or an annuity • We can find the present or future value of such a stream by using the principle of value additivity
Uneven Cash Flows: An Example (1) • Assume that an investment offers the following cash flows. If your required return is 7%, what is the maximum price that you would pay for this investment? 100 0 1 200 2 300 3 4 5
Uneven Cash Flows: An Example (2) • Suppose that you were to deposit the following amounts in an account paying 5% per year. What would the balance of the account be at the end of the third year? 300 0 1 500 2 700 3 4 5
Non-annual Compounding • So far we have assumed that the time period is equal to a year • However, there is no reason that a time period can’t be any other length of time • We could assume that interest is earned semi-annually, quarterly, monthly, daily, or any other length of time • The only change that must be made is to make sure that the rate of interest is adjusted to the period length
Non-annual Compounding (cont. ) • Suppose that you have $1, 000 available for investment. After investigating the local banks, you have compiled the following table for comparison. In which bank should you deposit your funds?
Non-annual Compounding (cont. ) • To solve this problem, you need to determine which bank will pay you the most interest • In other words, at which bank will you have the highest future value? • To find out, let’s change our basic FV equation slightly: In this version of the equation ‘m’ is the number of compounding periods per year
Non-annual Compounding (cont. ) • We can find the FV for each bank as follows: First National Bank: Second National Bank: Third National Bank: Obviously, you should choose the Third National Bank
Continuous Compounding • There is no reason why we need to stop increasing the compounding frequency at daily • We could compound every hour, minute, or second • We can also compound every instant (i. e. , continuously): v Here, F is the future value, P is the present value, r is the annual rate of interest, t is the total number of years, and e is a constant equal to about 2. 718
Continuous Compounding (cont. ) • Suppose that the Fourth National Bank is offering to pay 10% per year compounded continuously. What is the future value of your $1, 000 investment? v v This is even better than daily compounding The basic rule of compounding is: The more frequently interest is compounded, the higher the future value
Continuous Compounding (cont. ) • Suppose that the Fourth National Bank is offering to pay 10% per year compounded continuously. If you plan to leave the money in the account for 5 years, what is the future value of your $1, 000 investment?