The Theory of Supernova Remnants è Some comments

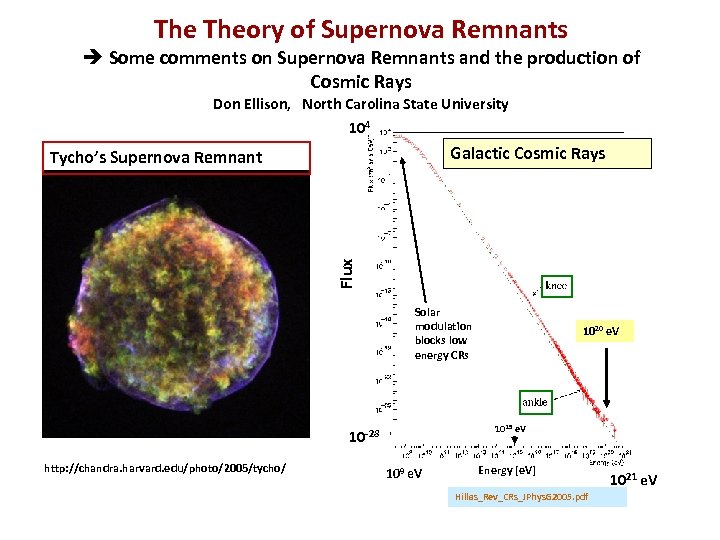The Theory of Supernova Remnants è Some comments on Supernova Remnants and the production of Cosmic Rays Don Ellison, North Carolina State University 104 Galactic Cosmic Rays Flux Tycho’s Supernova Remnant Solar modulation blocks low energy CRs 1015 e. V 10 -28 http: //chandra. harvard. edu/photo/2005/tycho/ 1020 e. V 109 e. V Energy [e. V] Hillas_Rev_CRs_JPhys. G 2005. pdf 1021 e. V

Consider efficient production of Cosmic Rays by Diffusive Shock Acceleration (DSA) in SNRs DSA is also called the first-order Fermi mechanism Particle acceleration in Collisionless Shocks Many 100’s of references. Some review papers: Axford 1981; Drury 1983; Blandford & Eichler 1987; Jones & Ellison 1991; Berezhko & Ellison 1999; Malkov & Drury 2001; Bykov 2004; Bykov et al 2011, 2012, 2013 Discovery papers for first-order Fermi mechanism in shocks: Krymskii (1976), Axford, Leer & Skadron (1977), Bell (1978), Blandford & Ostriker (1978) So called “Universal” test-particle power law for particles (in a strong shock) If particles are fully relativistic: Don Ellison, NCSU

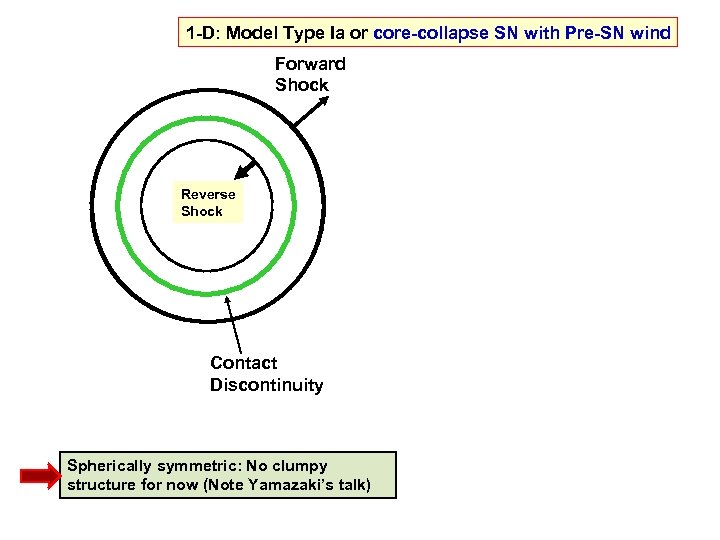1 -D: Model Type Ia or core-collapse SN with Pre-SN wind Forward Shock Reverse Shock Contact Discontinuity Spherically symmetric: No clumpy structure for now (Note Yamazaki’s talk)

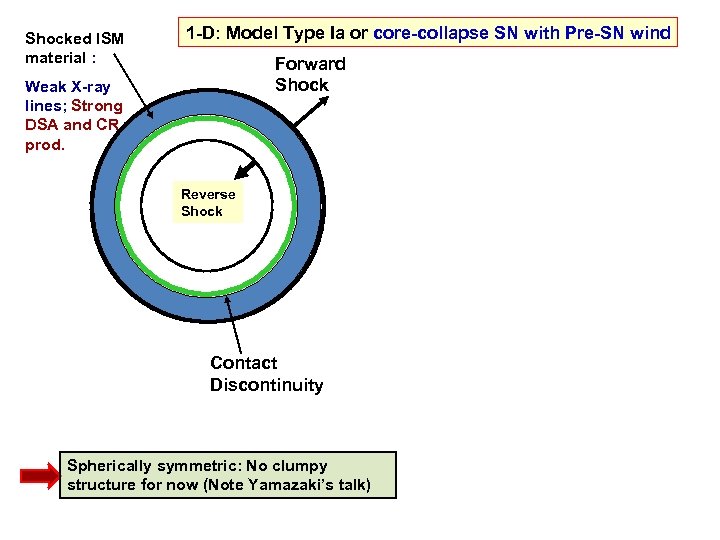Shocked ISM material : 1 -D: Model Type Ia or core-collapse SN with Pre-SN wind Forward Shock Weak X-ray lines; Strong DSA and CR prod. Reverse Shock Contact Discontinuity Spherically symmetric: No clumpy structure for now (Note Yamazaki’s talk)

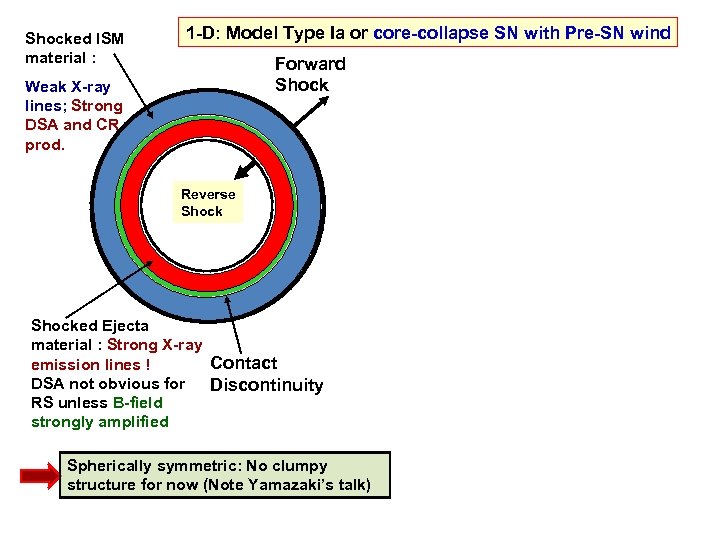Shocked ISM material : 1 -D: Model Type Ia or core-collapse SN with Pre-SN wind Forward Shock Weak X-ray lines; Strong DSA and CR prod. Reverse Shocked Ejecta material : Strong X-ray Contact emission lines ! DSA not obvious for Discontinuity RS unless B-field strongly amplified Spherically symmetric: No clumpy structure for now (Note Yamazaki’s talk)

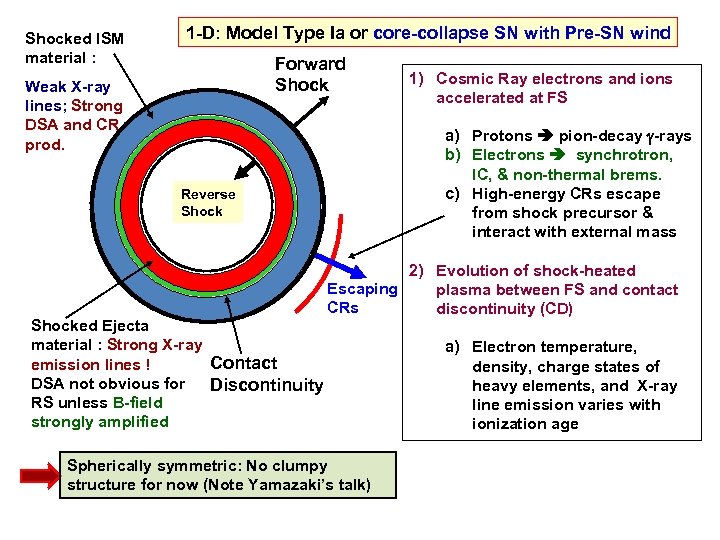Shocked ISM material : 1 -D: Model Type Ia or core-collapse SN with Pre-SN wind Forward Shock Weak X-ray lines; Strong DSA and CR prod. a) Protons pion-decay -rays b) Electrons synchrotron, IC, & non-thermal brems. c) High-energy CRs escape from shock precursor & interact with external mass Reverse Shocked Ejecta material : Strong X-ray Contact emission lines ! DSA not obvious for Discontinuity RS unless B-field strongly amplified 1) Cosmic Ray electrons and ions accelerated at FS 2) Evolution of shock-heated Escaping plasma between FS and contact CRs discontinuity (CD) Spherically symmetric: No clumpy structure for now (Note Yamazaki’s talk) a) Electron temperature, density, charge states of heavy elements, and X-ray line emission varies with ionization age

Main effects from DSA that influence SNR hydrodynamics : 1) Nonthermal particles (i. e. , swept-up ISM or ejecta) are turned into relativistic CRs by DSA. This lowers specific heat ratio (5/3 4/3) 2) Some of the highest energy CRs will escape upstream from the forward shock. This also lowers specific heat ratio (4/3 1) Effects (1) and (2) cause the shock compression ratio to increase above r = 4 (find typical values with efficient DSA : r ~ 5 - 10 ) 3) If DSA is efficient, to conserve energy, temperature of shocked gas MUST decrease below value expected without CR production SNR shocks that efficiently produce CRs will have large compression ratios and low shocked temperatures Production of CRs influences SNR hydrodynamics & thermal X -ray emission Don Ellison, NCSU

Test-particle power law hardens with increasing comp. ratio, r ► For strong shocks, “universal power law” diverges unless acceleration stopped by finite size or finite age. “Universal” power law diverges for r = 4 Diverges for strong shocks with compression ratio r 4 In strong shocks, CRs must modify the shock, and some of the highest energy CRs must escape if acceleration is efficient strong nonlinear effects

What happens to the test-particle prediction when nonlinear effects are taken into account? First: Collisionless plasmas :

Collisionless plasmas : NGC 2736: The Pencil Nebula We see “thin” structures in solar wind and ISM : e. g. , planetary bow shocks and SNR shocks The length scale of these structures must be many orders of magnitude smaller than the collisional mean-free-path Thin structures are possible because wave -particle interactions produce short mfp for particle isotropization Hydrogen emission SN 1006

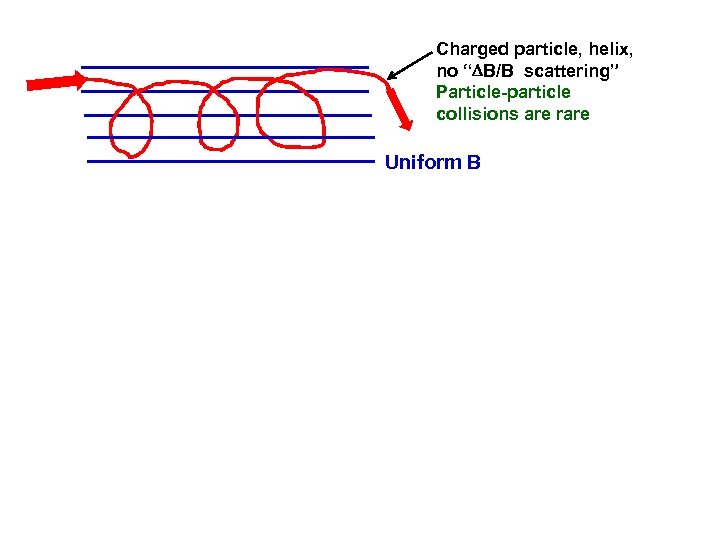Charged particle, helix, no “ B/B scattering” Particle-particle collisions are rare Uniform B

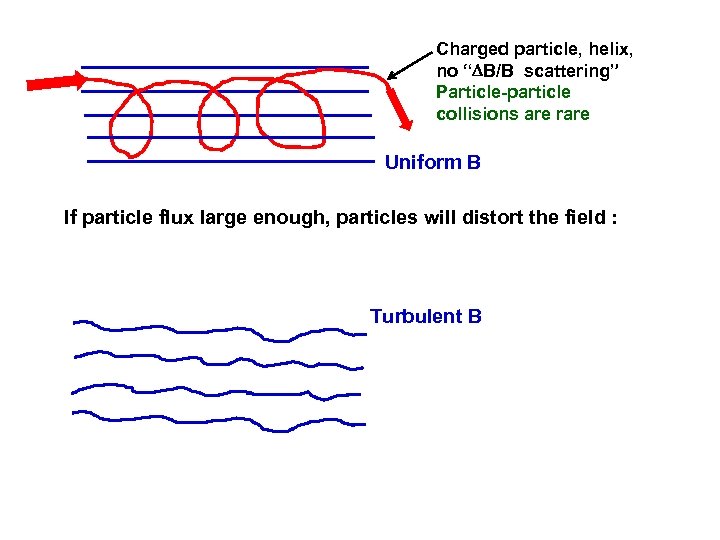Charged particle, helix, no “ B/B scattering” Particle-particle collisions are rare Uniform B If particle flux large enough, particles will distort the field : Turbulent B

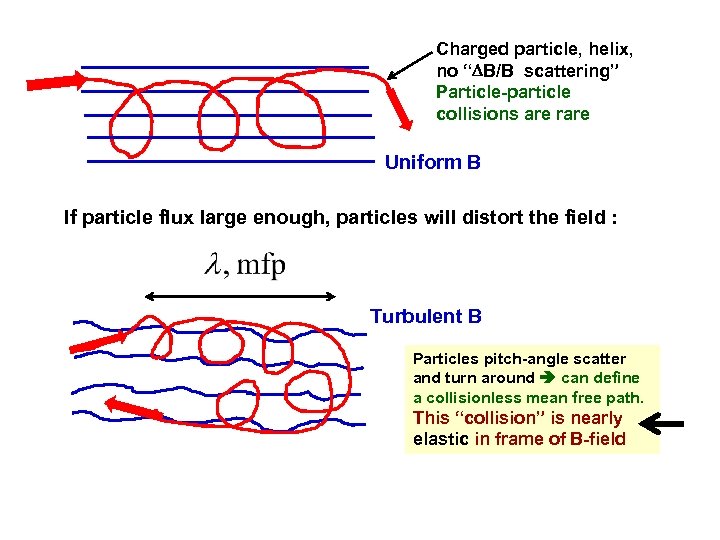Charged particle, helix, no “ B/B scattering” Particle-particle collisions are rare Uniform B If particle flux large enough, particles will distort the field : Turbulent B Particles pitch-angle scatter and turn around can define a collisionless mean free path. This “collision” is nearly elastic in frame of B-field

In collision-dominated plasmas, particle-particle collisions drive the plasma to thermal equilibrium. If an individual particle gets more energy than average, it will immediately transfer energy via collisions to slower particles scatterings are Inelastic In a collisionless plasma, particles interact with the background B-field one proton “scatters” off of ~ Avogadro’s number of particles tied together by nearly “frozen-in” turbulent B-field scatterings are nearly elastic An individual particle can gain, and keep for long times, much more energy than an average thermal particle B-fields are frozen-in because of high conductivity of diffuse plasmas. If the plasma moves, currents are generated to produce B-fields so magnetic flux remains unchanged. B-field moves with bulk plasma

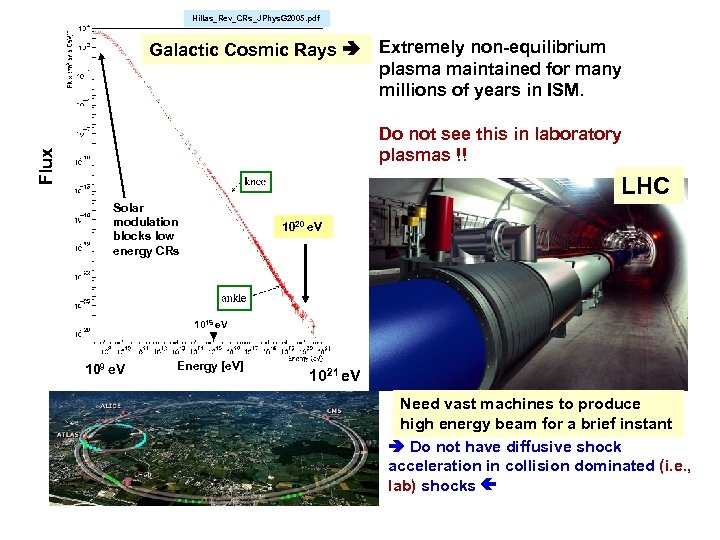Hillas_Rev_CRs_JPhys. G 2005. pdf Galactic Cosmic Rays Extremely non-equilibrium plasma maintained for many millions of years in ISM. Flux Do not see this in laboratory plasmas !! LHC Solar modulation blocks low energy CRs 1020 e. V 1015 e. V 109 e. V Energy [e. V] 1021 e. V Need vast machines to produce high energy beam for a brief instant Do not have diffusive shock acceleration in collision dominated (i. e. , lab) shocks

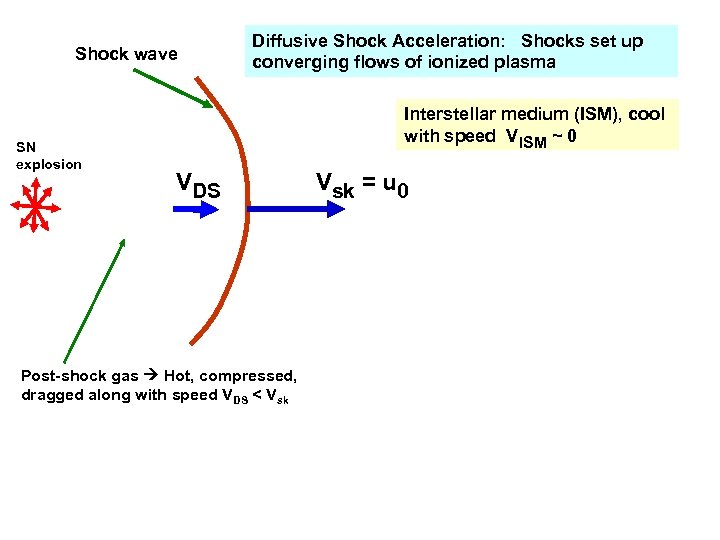Shock wave SN explosion Diffusive Shock Acceleration: Shocks set up converging flows of ionized plasma Interstellar medium (ISM), cool with speed VISM ~ 0 VDS Post-shock gas Hot, compressed, dragged along with speed VDS < Vsk = u 0

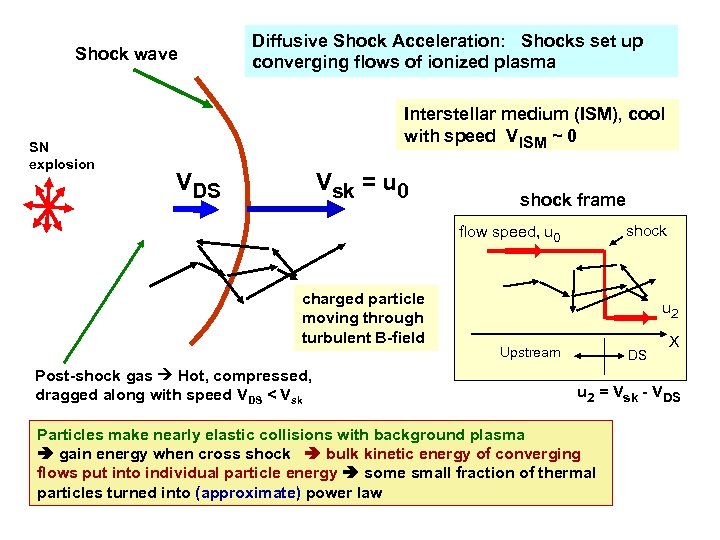Shock wave SN explosion Diffusive Shock Acceleration: Shocks set up converging flows of ionized plasma Interstellar medium (ISM), cool with speed VISM ~ 0 VDS Vsk = u 0 shock frame shock flow speed, u 0 charged particle moving through turbulent B-field Post-shock gas Hot, compressed, dragged along with speed VDS < Vsk u 2 Upstream DS X u 2 = Vsk - VDS Particles make nearly elastic collisions with background plasma gain energy when cross shock bulk kinetic energy of converging flows put into individual particle energy some small fraction of thermal particles turned into (approximate) power law

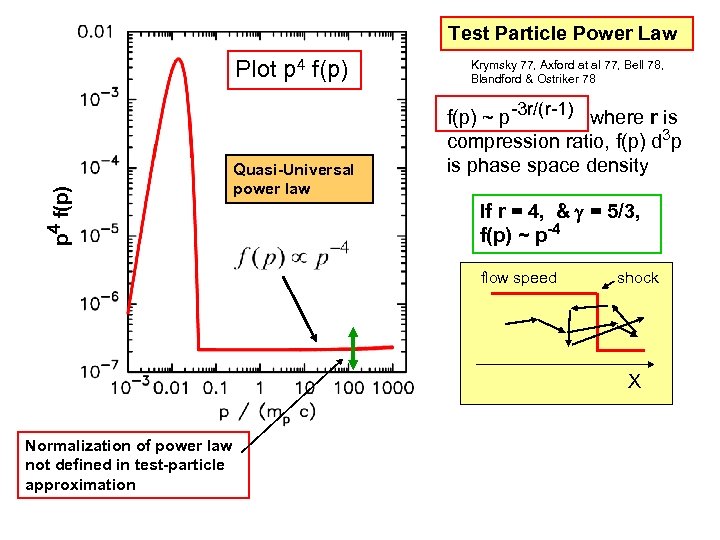Test Particle Power Law p 4 f(p) Plot p 4 f(p) Quasi-Universal power law Krymsky 77, Axford at al 77, Bell 78, Blandford & Ostriker 78 f(p) ~ p-3 r/(r-1) where r is compression ratio, f(p) d 3 p is phase space density If r = 4, & = 5/3, f(p) ~ p-4 flow speed shock X Normalization of power law not defined in test-particle approximation

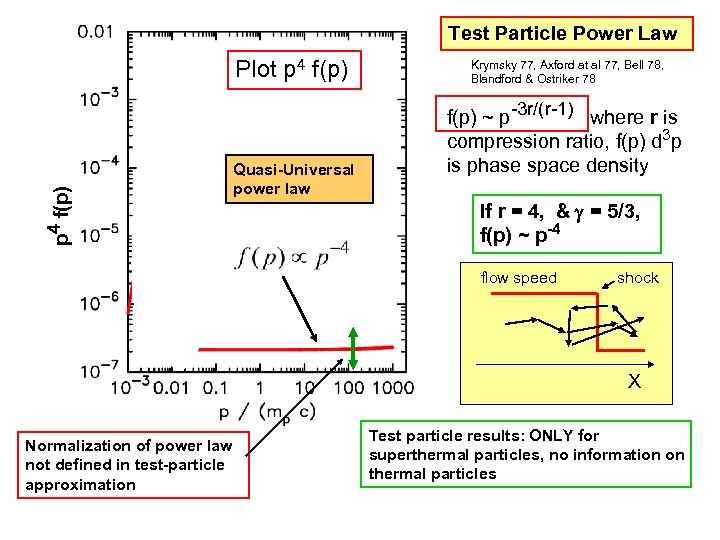Test Particle Power Law p 4 f(p) Plot p 4 f(p) Quasi-Universal power law Krymsky 77, Axford at al 77, Bell 78, Blandford & Ostriker 78 f(p) ~ p-3 r/(r-1) where r is compression ratio, f(p) d 3 p is phase space density If r = 4, & = 5/3, f(p) ~ p-4 flow speed shock X Normalization of power law not defined in test-particle approximation Test particle results: ONLY for superthermal particles, no information on thermal particles

p 4 f(p) [f(p) is phase space distr. ] Temperature p 4 f(p) If acceleration is efficient, shock becomes smooth from backpressure of CRs Flow speed test particle shock subshock X NL TP: f(p) p-4 ► Concave spectrum ► Compression ratio, rtot > 4 ► Low shocked temp. rsub < 4 B-field effects may reduce curvature In efficient acceleration, entire particle spectrum must be described consistently, including escaping particles much harder mathematically BUT, connects thermal emission to radio & Ge. V-Te. V emission

Efficient acceleration shock becomes smooth from CR backpressure Flow speed test particle shock subshock X Weak subshock, r < 4 lower shocked temperature Overall compression ratio > 4 higher shocked density Temperature and density determine non-equilibrium ionization state of shocked plasma SNR evolution & X-ray emission modified by efficient shock acceleration èCaution: while basic predictions are extremely robust – They only depend on particle diffusion length being increasing function of energy, è Size of nonlinear effects depend on acceleration efficiency.

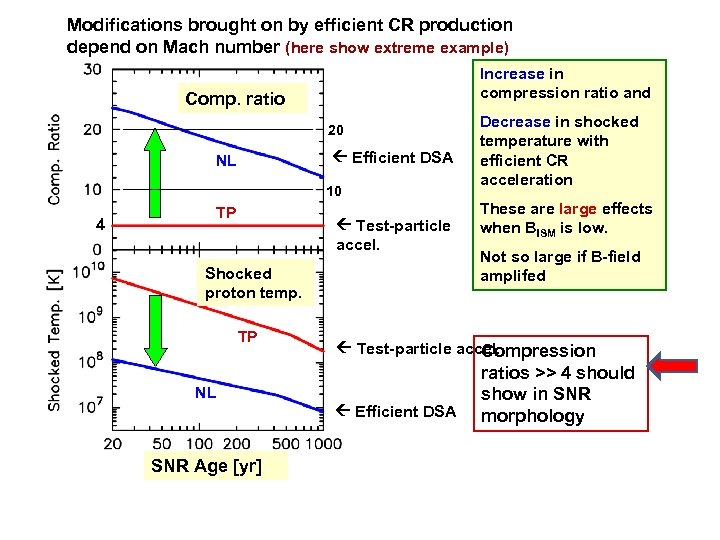Modifications brought on by efficient CR production depend on Mach number (here show extreme example) Increase in compression ratio and Comp. ratio 20 Efficient DSA NL 10 4 TP Test-particle accel. Shocked proton temp. TP These are large effects when BISM is low. Not so large if B-field amplifed Test-particle accel. Compression NL Efficient DSA SNR Age [yr] Decrease in shocked temperature with efficient CR acceleration ratios >> 4 should show in SNR morphology

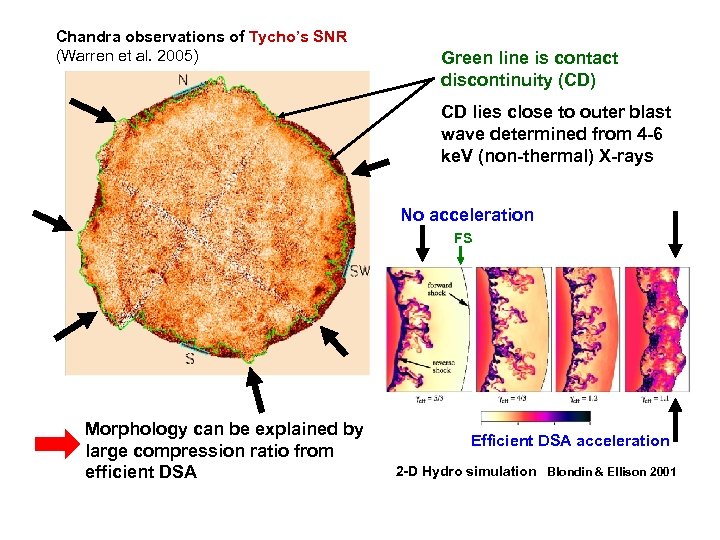Chandra observations of Tycho’s SNR (Warren et al. 2005) Green line is contact discontinuity (CD) CD lies close to outer blast wave determined from 4 -6 ke. V (non-thermal) X-rays No acceleration FS Morphology can be explained by large compression ratio from efficient DSA Efficient DSA acceleration 2 -D Hydro simulation Blondin & Ellison 2001

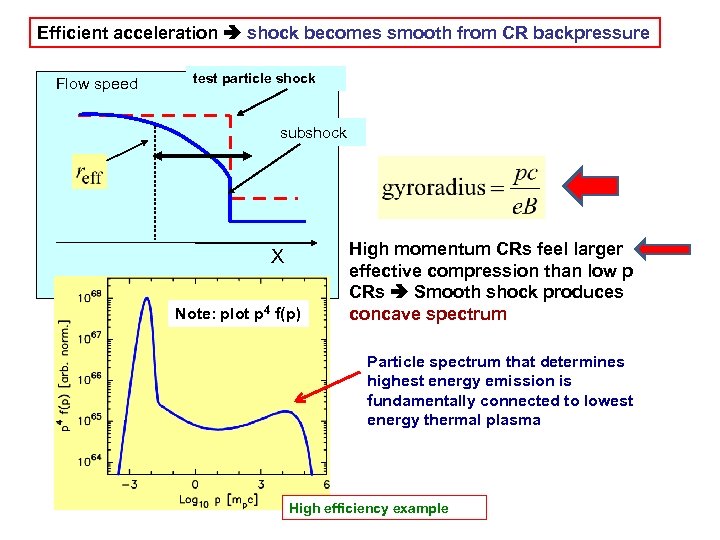Efficient acceleration shock becomes smooth from CR backpressure Flow speed test particle shock subshock X Note: plot p 4 f(p) High momentum CRs feel larger effective compression than low p CRs Smooth shock produces concave spectrum Particle spectrum that determines highest energy emission is fundamentally connected to lowest energy thermal plasma High efficiency example

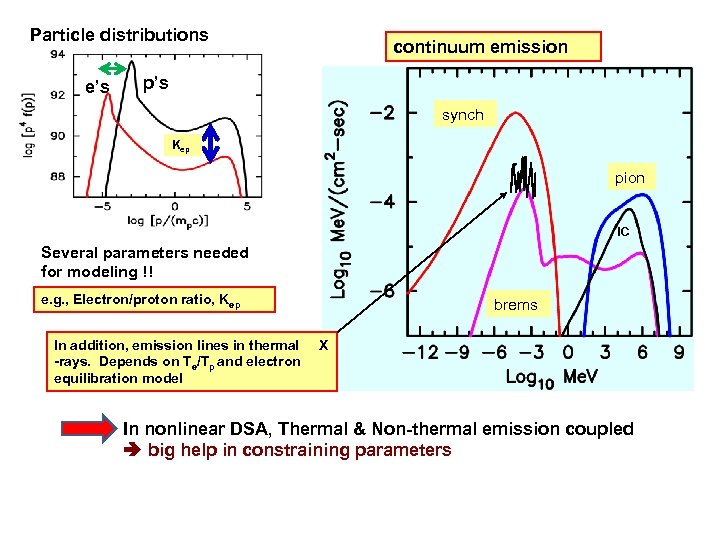Particle distributions e’s continuum emission p’s synch Kep pion IC Several parameters needed for modeling !! e. g. , Electron/proton ratio, Kep In addition, emission lines in thermal -rays. Depends on Te/Tp and electron equilibration model brems X In nonlinear DSA, Thermal & Non-thermal emission coupled big help in constraining parameters

Have developed a Composite SNR Model (CR-hydro-NEI code) SNR hydrodynamics, Nonlinear Shock Acceleration, Broadband continuum radiation, and X-ray emission line Collaborators: Andrei Bykov, Daniel Castro, Herman Lee, Hiro Nagataki, Dan Patnaude, & Pat Slane (early work with: Anne Decourchelle & Jean Ballet 2000, 2004) 1) VH-1 code for 1 -D hydrodynamics of evolving SNR (e. g. , J. Blondin) 2) Semi-analytic, nonlinear DSA model (from P. Blasi and co-workers) 3) Non-equilibrium ionization for X-ray line emission (D. Patnaude, J. Raymond) 4) NL shock acceleration coupled to SNR hydrodynamics (Herman Lee) 5) Magnetic field amplification (Blasi’s group & Andrei Bykov) 6) Electron and Ion distributions from thermal to relativistic energies (T. Kamae) 7) Continuum photon emission from radio to Te. V 8) Simple model of escaping CRs propagating beyond SNR Apply model to individual SNRs: RX J 1713, CTB 109, Vela Jr. , Tycho

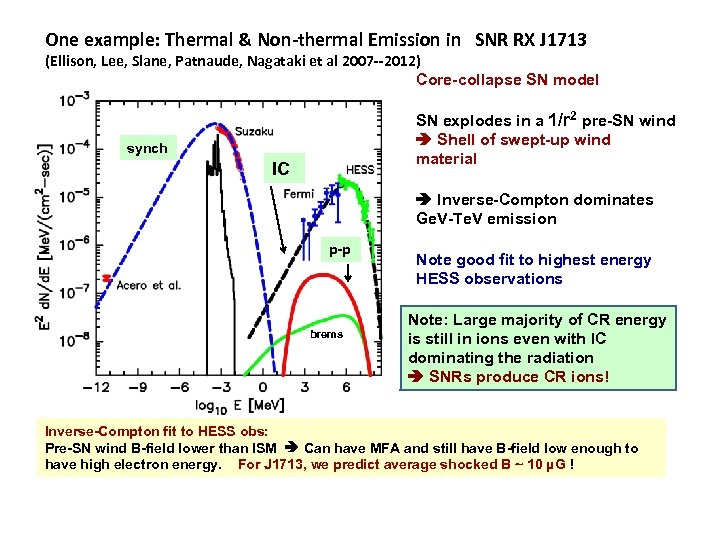One example: Thermal & Non-thermal Emission in SNR RX J 1713 (Ellison, Lee, Slane, Patnaude, Nagataki et al 2007 --2012) Core-collapse SN model SN explodes in a 1/r 2 pre-SN wind Shell of swept-up wind material synch IC Inverse-Compton dominates Ge. V-Te. V emission p-p brems Note good fit to highest energy HESS observations Note: Large majority of CR energy is still in ions even with IC dominating the radiation SNRs produce CR ions! Inverse-Compton fit to HESS obs: Pre-SN wind B-field lower than ISM Can have MFA and still have B-field low enough to have high electron energy. For J 1713, we predict average shocked B ~ 10 µG !

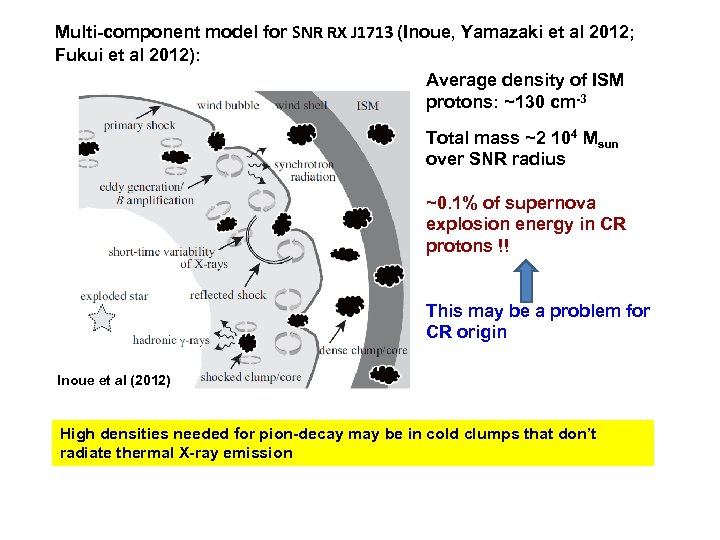Multi-component model for SNR RX J 1713 (Inoue, Yamazaki et al 2012; Fukui et al 2012): Average density of ISM protons: ~130 cm-3 Total mass ~2 104 Msun over SNR radius ~0. 1% of supernova explosion energy in CR protons !! This may be a problem for CR origin Inoue et al (2012) High densities needed for pion-decay may be in cold clumps that don’t radiate thermal X-ray emission

Warning: many parameters and uncertainties in CR-hydro-NEI model, but : For spherically symmetric model of SNR RX J 1713 & Vela Jr. : Inverse-Compton is best explanation for Ge. V-Te. V Other remnants can certainly be Hadronic or mixed, e. g. Tycho’s SNR and CTB 109. Important: For DSA most CR energy (~17% of ESN for J 1713) is in ions even with inverse-Compton dominating the radiation All nonlinear models show that SNRs produce CR ions !!! There is no fundamental difference between IC and pp dominated SNRs Besides question of CR origin: Careful modeling of SNRs can provide constraints on critical parameters for shock acceleration: a) Shape and normalization of CR ions from particular SNRs b) electron/proton injection ratio c) Acceleration efficiency d) Magnetic Field Amplification e) Properties of escaping CRs f) Geometry effects in SNRs such as SN 1006 What about CRs observed at Earth? CREAM Balloon flights

CREAM Balloon flights in Antarctica 40 million cubic foot balloon Float between ~38 and ~40 km Average atmospheric overburden of ~3. 9 g/cm 2 Total exposure for 5 flights ~156 days

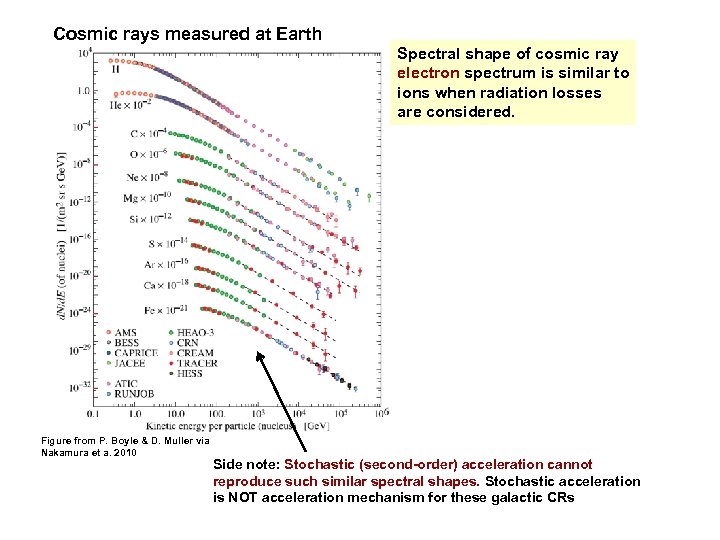Cosmic rays measured at Earth Spectral shape of cosmic ray electron spectrum is similar to ions when radiation losses are considered. Figure from P. Boyle & D. Muller via Nakamura et a. 2010 Side note: Stochastic (second-order) acceleration cannot reproduce such similar spectral shapes. Stochastic acceleration is NOT acceleration mechanism for these galactic CRs

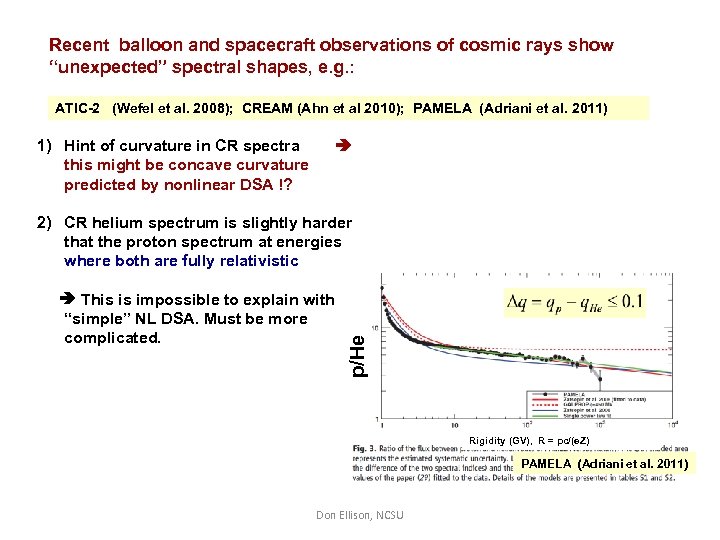Recent balloon and spacecraft observations of cosmic rays show “unexpected” spectral shapes, e. g. : ATIC-2 (Wefel et al. 2008); CREAM (Ahn et al 2010); PAMELA (Adriani et al. 2011) 1) Hint of curvature in CR spectra this might be concave curvature predicted by nonlinear DSA !? This is impossible to explain with “simple” NL DSA. Must be more complicated. p/He 2) CR helium spectrum is slightly harder that the proton spectrum at energies where both are fully relativistic Rigidity (GV), R = pc/(e. Z) PAMELA (Adriani et al. 2011) Don Ellison, NCSU

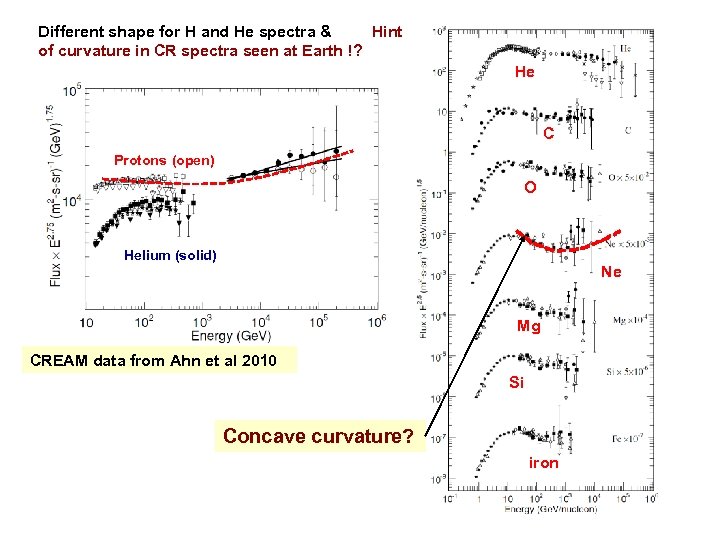Different shape for H and He spectra & Hint of curvature in CR spectra seen at Earth !? He C Protons (open) O Helium (solid) Ne Mg CREAM data from Ahn et al 2010 Si Concave curvature? iron

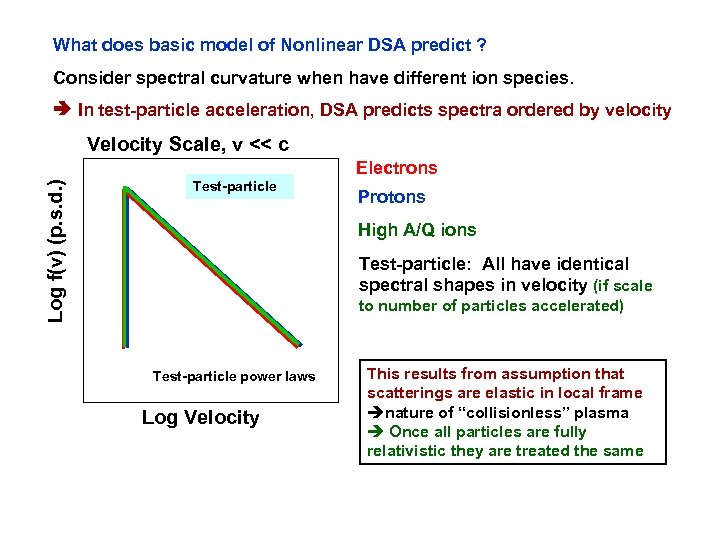What does basic model of Nonlinear DSA predict ? Consider spectral curvature when have different ion species. In test-particle acceleration, DSA predicts spectra ordered by velocity Velocity Scale, v << c Log f(v) (p. s. d. ) Electrons Test-particle Protons High A/Q ions Test-particle: All have identical spectral shapes in velocity (if scale to number of particles accelerated) Test-particle power laws Log Velocity This results from assumption that scatterings are elastic in local frame ènature of “collisionless” plasma è Once all particles are fully relativistic they are treated the same

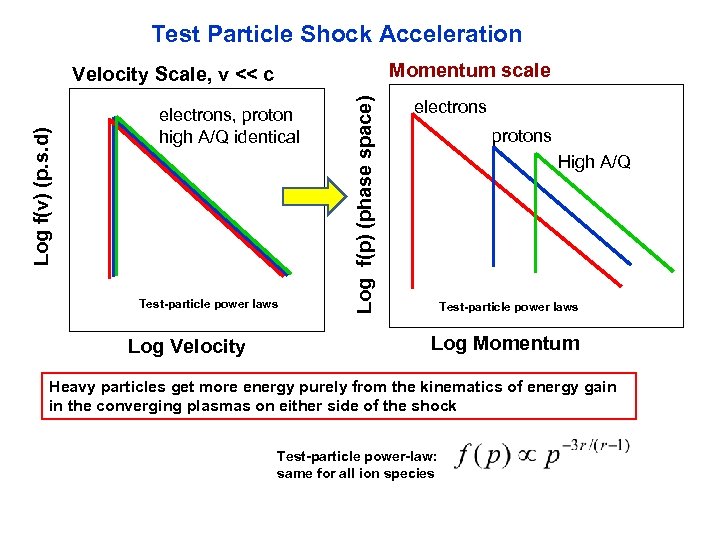Test Particle Shock Acceleration Momentum scale electrons, proton high A/Q identical Test-particle power laws Log Velocity Log f(p) (phase space) Log f(v) (p. s. d) Velocity Scale, v << c electrons protons High A/Q Test-particle power laws Log Momentum Heavy particles get more energy purely from the kinematics of energy gain in the converging plasmas on either side of the shock Test-particle power-law: same for all ion species

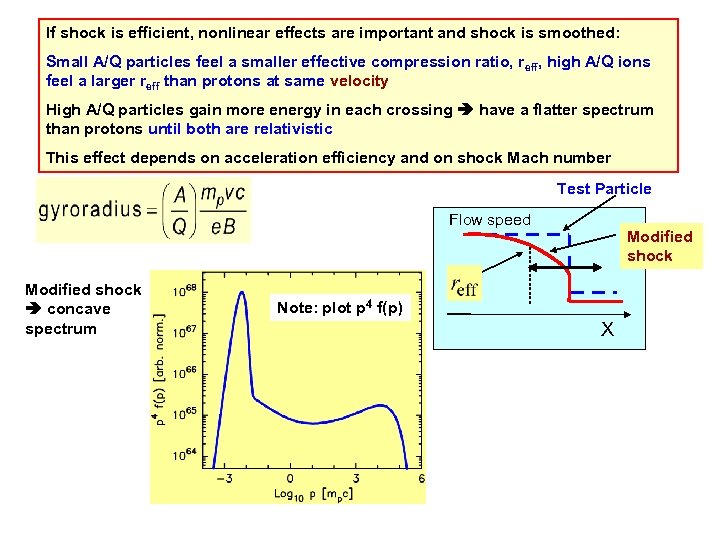If shock is efficient, nonlinear effects are important and shock is smoothed: Small A/Q particles feel a smaller effective compression ratio, reff, high A/Q ions feel a larger reff than protons at same velocity High A/Q particles gain more energy in each crossing have a flatter spectrum than protons until both are relativistic This effect depends on acceleration efficiency and on shock Mach number Test Particle Flow speed Modified shock concave spectrum Modified shock Note: plot p 4 f(p) X

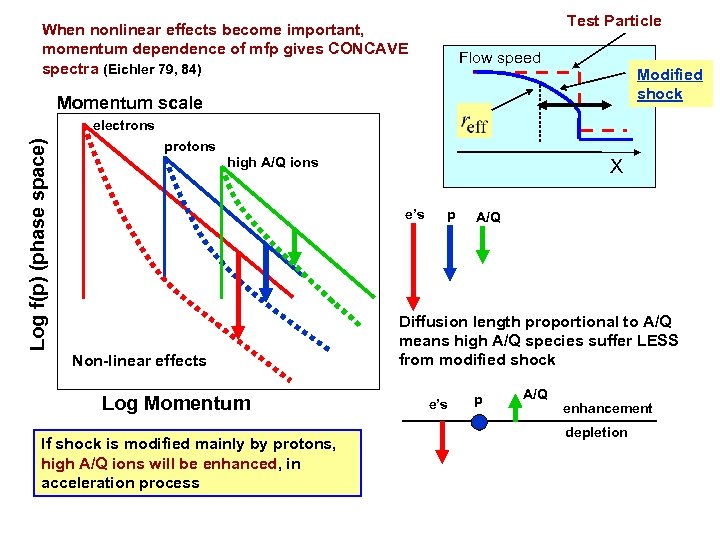Test Particle When nonlinear effects become important, momentum dependence of mfp gives CONCAVE spectra (Eichler 79, 84) Flow speed Modified shock Momentum scale Log f(p) (phase space) electrons protons high A/Q ions X e’s Non-linear effects Log Momentum If shock is modified mainly by protons, high A/Q ions will be enhanced, in acceleration process p A/Q Diffusion length proportional to A/Q means high A/Q species suffer LESS from modified shock e’s p A/Q enhancement depletion

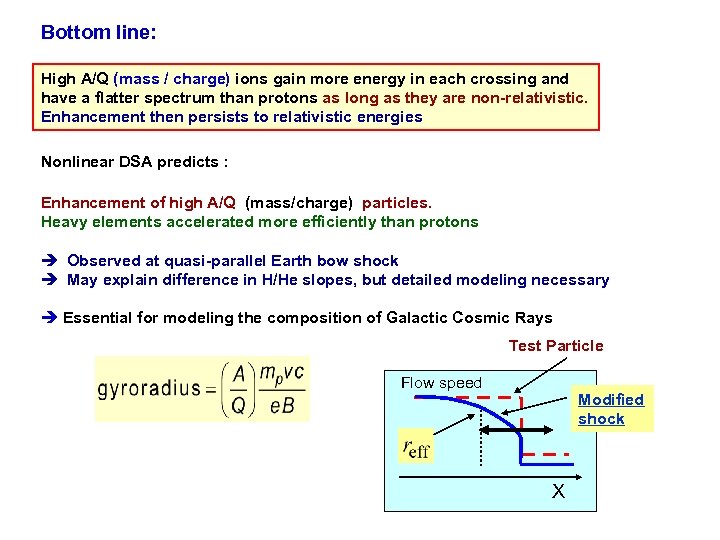Bottom line: High A/Q (mass / charge) ions gain more energy in each crossing and have a flatter spectrum than protons as long as they are non-relativistic. Enhancement then persists to relativistic energies Nonlinear DSA predicts : Enhancement of high A/Q (mass/charge) particles. Heavy elements accelerated more efficiently than protons è Observed at quasi-parallel Earth bow shock è May explain difference in H/He slopes, but detailed modeling necessary è Essential for modeling the composition of Galactic Cosmic Rays Test Particle Flow speed Modified shock X

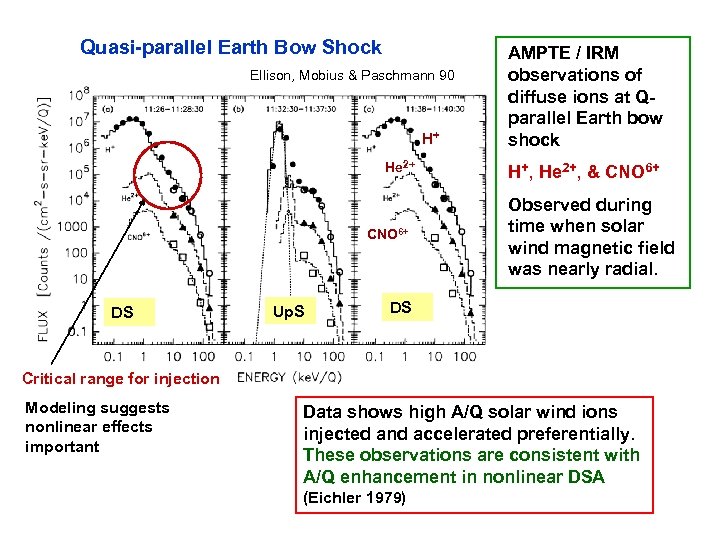Quasi-parallel Earth Bow Shock Ellison, Mobius & Paschmann 90 H+ He 2+ CNO 6+ DS Up. S AMPTE / IRM observations of diffuse ions at Qparallel Earth bow shock H+, He 2+, & CNO 6+ Observed during time when solar wind magnetic field was nearly radial. DS Critical range for injection Modeling suggests nonlinear effects important Data shows high A/Q solar wind ions injected and accelerated preferentially. These observations are consistent with A/Q enhancement in nonlinear DSA (Eichler 1979)

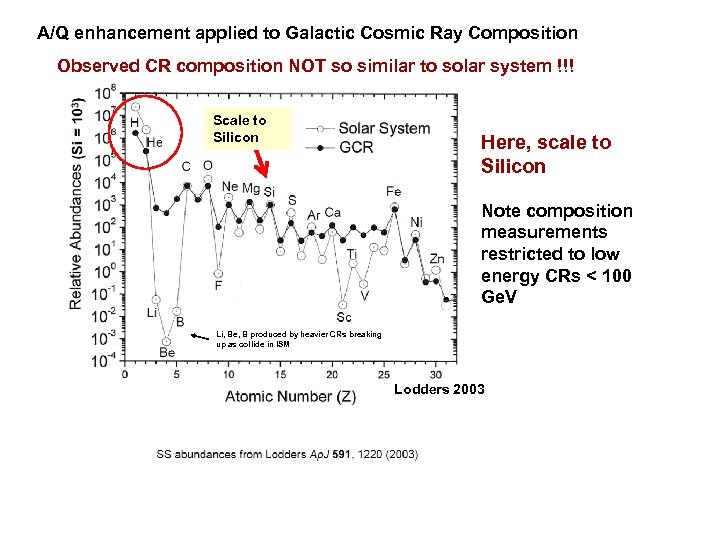A/Q enhancement applied to Galactic Cosmic Ray Composition Observed CR composition NOT so similar to solar system !!! Scale to Silicon Here, scale to Silicon Note composition measurements restricted to low energy CRs < 100 Ge. V Li, Be, B produced by heavier CRs breaking up as collide in ISM Lodders 2003

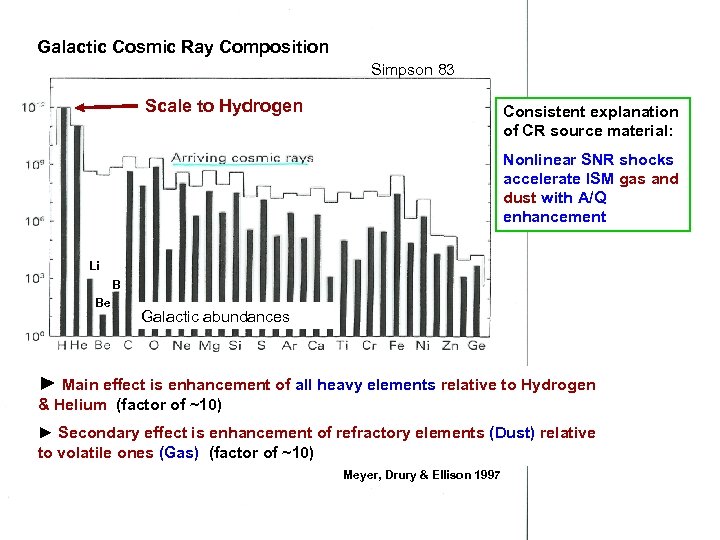Galactic Cosmic Ray Composition Simpson 83 Scale to Hydrogen Consistent explanation of CR source material: Nonlinear SNR shocks accelerate ISM gas and dust with A/Q enhancement Li B Be Galactic abundances ► Main effect is enhancement of all heavy elements relative to Hydrogen & Helium (factor of ~10) ► Secondary effect is enhancement of refractory elements (Dust) relative to volatile ones (Gas) (factor of ~10) Meyer, Drury & Ellison 1997

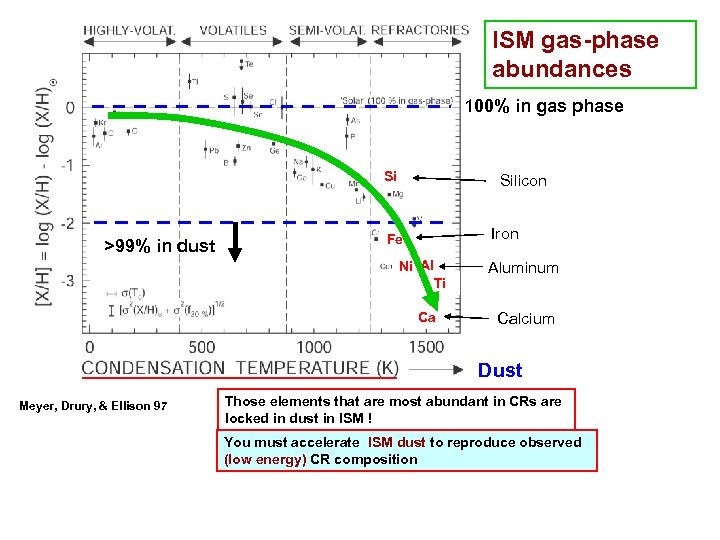ISM gas-phase abundances 100% in gas phase Si >99% in dust Silicon Iron Fe Ni Al Ti Ca Aluminum Calcium Dust Meyer, Drury, & Ellison 97 Those elements that are most abundant in CRs are locked in dust in ISM ! You must accelerate ISM dust to reproduce observed (low energy) CR composition

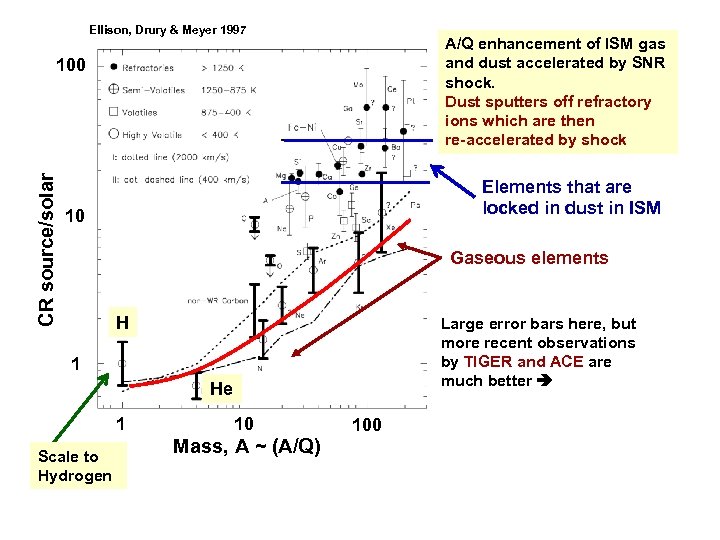Ellison, Drury & Meyer 1997 A/Q enhancement of ISM gas and dust accelerated by SNR shock. Dust sputters off refractory ions which are then re-accelerated by shock CR source/solar 100 Elements that are locked in dust in ISM 10 Gaseous elements H Large error bars here, but more recent observations by TIGER and ACE are much better 1 He 1 Scale to Hydrogen 10 Mass, A ~ (A/Q) 100

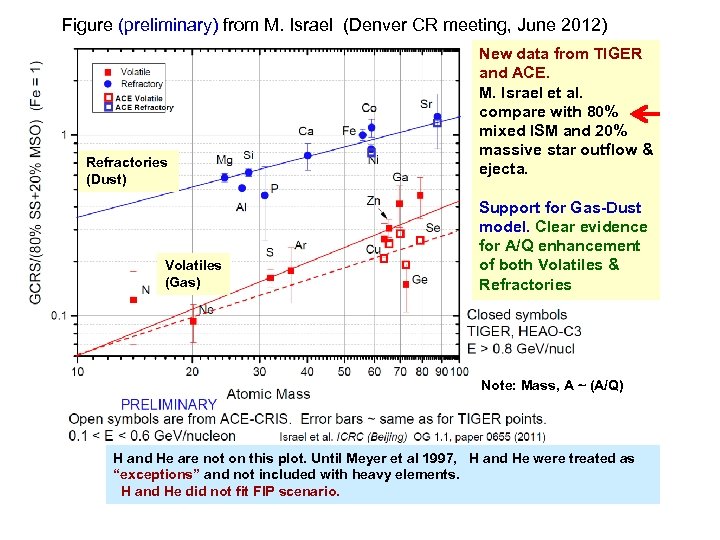Figure (preliminary) from M. Israel (Denver CR meeting, June 2012) Refractories (Dust) Volatiles (Gas) New data from TIGER and ACE. M. Israel et al. compare with 80% mixed ISM and 20% massive star outflow & ejecta. Support for Gas-Dust model. Clear evidence for A/Q enhancement of both Volatiles & Refractories Note: Mass, A ~ (A/Q) H and He are not on this plot. Until Meyer et al 1997, H and He were treated as “exceptions” and not included with heavy elements. H and He did not fit FIP scenario.

Magnetic Field Amplification (MFA): Particle acceleration requires magnetic turbulence to work. This turbulence must be far stronger than typical ISM B/B to produce CRs to high energy Shocks can, and do, produce their own turbulence. No independent, external source of turbulence is necessary for DSA to take place. When a supersonic plasma, even one with zero B-field, encounters a barrier : è currents will be generated by particles reflecting off barrier, è small-scale B-fields result (call this the Weibel instability if you like), è fresh, unshocked particles now gyrate in these fields and become randomized, è a shock quickly forms, è particles start to be accelerated by the shock and the streaming instability generates more magnetic field, etc….

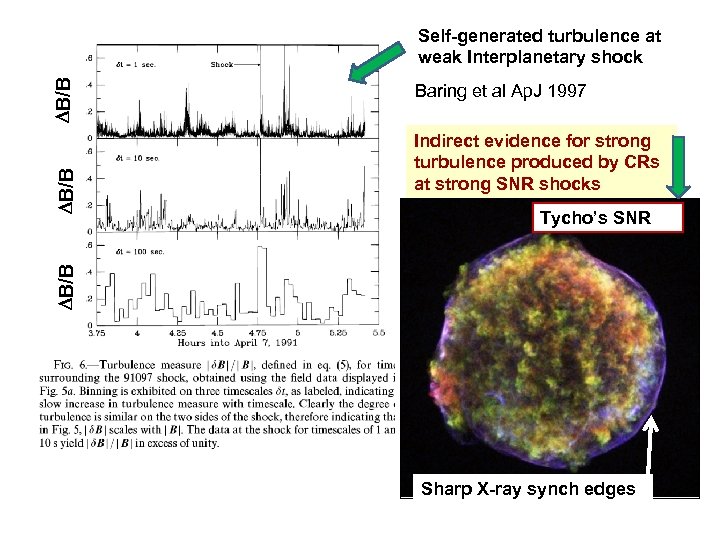Baring et al Ap. J 1997 Indirect evidence for strong turbulence produced by CRs at strong SNR shocks Tycho’s SNR B/B Self-generated turbulence at weak Interplanetary shock Sharp X-ray synch edges

How do you start with BISM 3 G and end up with B 300 G at the shock? Efficient diffusive shock acceleration (DSA) not only places a large fraction of shock energy into relativistic particles, but also amplifies magnetic field by large factors MFA is connected to efficient CR production, so nonlinear effects essential Bell & Lucek 2001 apply Q-linear theory when B/B >> 1; Bell 2004 non-resonant streaming instabilities Amato & Blasi 2006; Blasi, Amato & Caprioli 2006; Vladimirov, Ellison & Bykov 2006, 2008 } calculations coupled to nonlinear particle accel.

A lot of work by many people on nonlinear Diffusive Shock Acceleration (DSA) and Magnetic Field Amplification (MFA) Some current work (in no particular order): 1) 2) 3) 4) 5) 6) 7) 8) Amato, Blasi, Caprioli, Morlino, Vietri: Semi-analytic Bell: Semi-analytic and PIC simulations Berezhko, Volk, Ksenofontov: Semi-analytic Malkov: Semi-analytic Niemiec & Pohl: PIC Pelletier and co-workers: MHD, relativistic shocks Reville, Kirk & co-workers: MHD, PIC Spitkovsky and co-workers; Hoshino and co-workers; other PIC simulators: Particle-In-Cell simulations, so far, mainly rel. shocks 9) Caprioli & Spitkovsky; Giacalone et al. : hybrid simulations 10) Vladimirov, Ellison, Bykov: Monte Carlo 11) Zirakashvili & Ptuskin: Semi-analytic, MHD 12) Bykov et al 13) Apologies to people I missed …

Magnetic Field Amplification in DSA is a hard problem 1) Magnetic field generation intrinsic part of particle acceleration cannot treat DSA and MFA separately 2) Strong turbulence means Quasi-Linear Theory (QLT) not good approximation But QLT is our main analytic tool assumes B/B << 1) 3) Length and momentum scales are currently well beyond reach of 3 D particle-in-cell (PIC) simulations if wish to see full nonlinear effects Particularly true for non-relativistic shocks a) Problem difficult because Te. V protons influence injection of ke. V protons and electrons 4) To cover full dynamic range, must use approximate methods: e. g. , Monte Carlo, Semi-analytic, MHD simulations (QLT

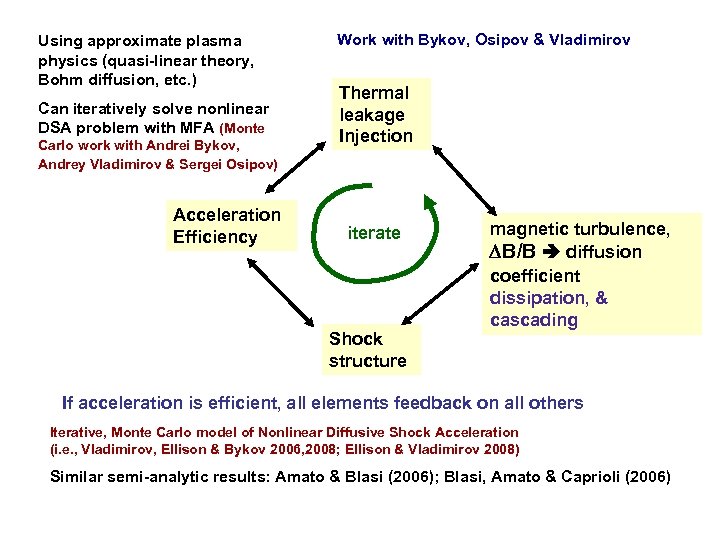Using approximate plasma physics (quasi-linear theory, Bohm diffusion, etc. ) Can iteratively solve nonlinear DSA problem with MFA (Monte Carlo work with Andrei Bykov, Andrey Vladimirov & Sergei Osipov) Acceleration Efficiency Work with Bykov, Osipov & Vladimirov Thermal leakage Injection iterate Shock structure magnetic turbulence, B/B diffusion coefficient dissipation, & cascading If acceleration is efficient, all elements feedback on all others Iterative, Monte Carlo model of Nonlinear Diffusive Shock Acceleration (i. e. , Vladimirov, Ellison & Bykov 2006, 2008; Ellison & Vladimirov 2008) Similar semi-analytic results: Amato & Blasi (2006); Blasi, Amato & Caprioli (2006)

Essential features of MFA in diffusive shock acceleration: 1) Production of turbulence, W(x, k) (assuming quasi-linear theory) a) Resonant (CR streaming instability) (e. g. , Skilling 75; Mc. Kenzie & Volk 82; Amato & Blasi 2006) b) Non-resonant current instabilities (e. g. , Bell 2004; Bykov et al. 2009; Reville et al 2007; Malkov & Diamond) i. ii. CR current produces waves with scales short compared to CR -radius CR current produces waves with scales long compared to CR radius gyro- 2) Calculation of D(x, p) once turbulence is known a) Resonant (QLT): Particles with gyro-radius ~ waves gives part ∝ p b) Non-resonant: Particles with gyro-radius >> waves gives part ∝ pσ 3) Production of turbulence and diffusion must be coupled to NL shock structure including injection of lowest energy particles and escape of highest energy All coupled (1) Thermal injection; (2) shock structure modified by back reaction of accelerated particles; (3) turbulence generation; (4) diffusion in self-generated turbulence; (5) escape of maximum energy particles All coupled

Conclusions: 1) The production of CRs in young SNRs is expected to be efficient and nonlinear: theory and observations support this in individual remnants 2) DSA is intrinsically efficient and difficult ! è Shock structure, CR production, B-field turbulence, Injection of thermal particles, all non-trivially connected 3) DSA is multi-scale (Intrinsic concave CR spectrum) Large fraction of total energy is in highest energy CRs with longest diffusion lengths To conserve energy, highest energy CRs must feedback on injection of lowest energy particles with shortest diffusion lengths 4) Injection of thermal particles, escape of high energy CRs, and self-generation of turbulence, all involve highly anisotropic distributions Quasi-linear theory not good approximation 5) Detailed plasma physics important for nonlinear effects, but : è Multi-scale nature currently beyond reach of PIC simulations 6) Need to know how NL DSA works to explain origin of CRs and to properly interpret broadband SNR observations (also radio jets, GRBs …. ) NL DSA influences the evolution and morphology of SNRs and thermal X-ray emission

Extra Slides

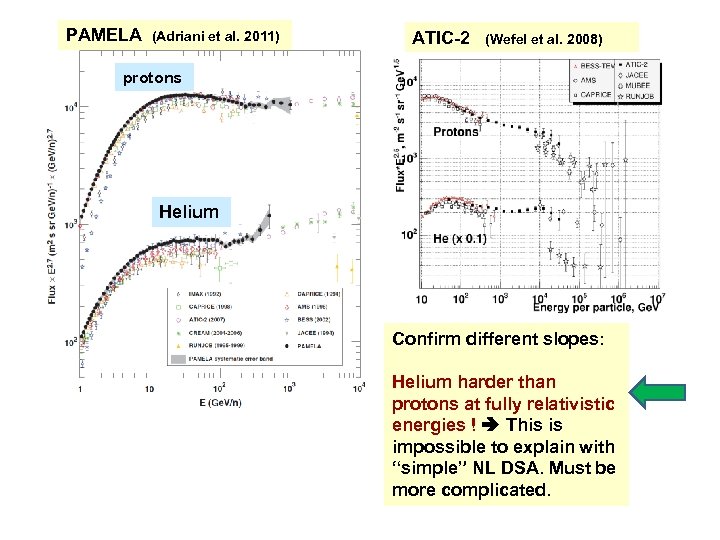PAMELA (Adriani et al. 2011) ATIC-2 (Wefel et al. 2008) protons Helium Confirm different slopes: Helium harder than protons at fully relativistic energies ! This is impossible to explain with “simple” NL DSA. Must be more complicated.

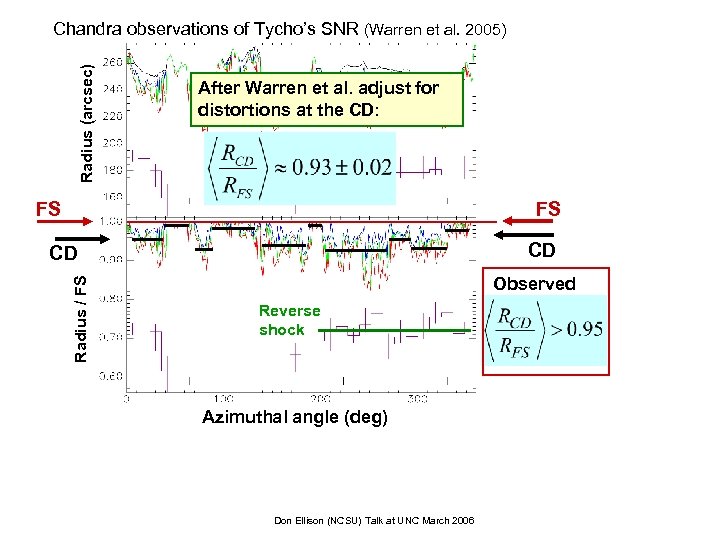Radius (arcsec) Chandra observations of Tycho’s SNR (Warren et al. 2005) After Warren et al. adjust for distortions at the CD: FS FS CD Radius / FS CD Observed Reverse shock Azimuthal angle (deg) Don Ellison (NCSU) Talk at UNC March 2006

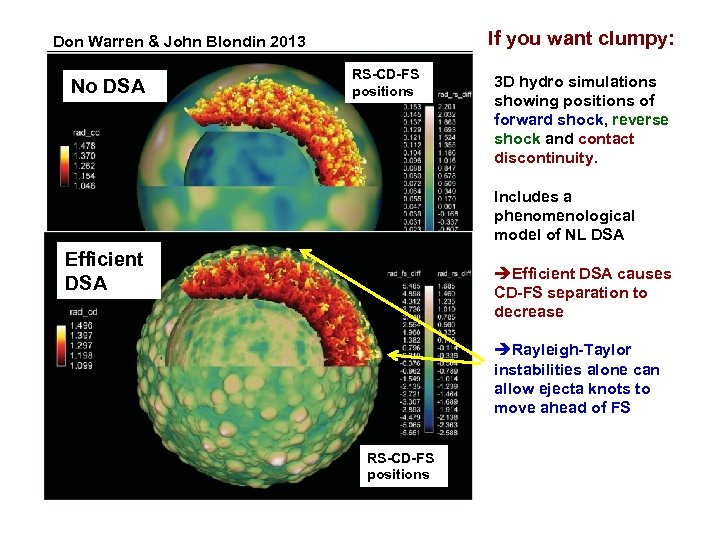If you want clumpy: Don Warren & John Blondin 2013 No DSA RS-CD-FS positions 3 D hydro simulations showing positions of forward shock, reverse shock and contact discontinuity. Includes a phenomenological model of NL DSA Efficient DSA èEfficient DSA causes CD-FS separation to decrease èRayleigh-Taylor instabilities alone can allow ejecta knots to move ahead of FS RS-CD-FS positions

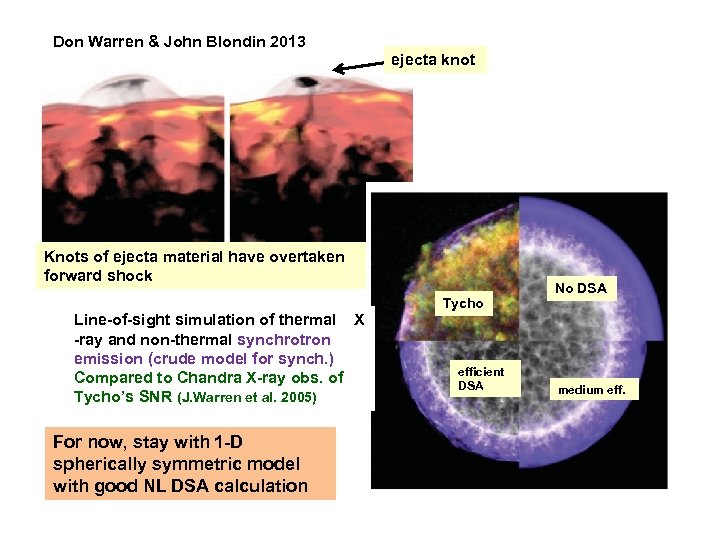Don Warren & John Blondin 2013 ejecta knot Knots of ejecta material have overtaken forward shock Line-of-sight simulation of thermal X -ray and non-thermal synchrotron emission (crude model for synch. ) Compared to Chandra X-ray obs. of Tycho’s SNR (J. Warren et al. 2005) For now, stay with 1 -D spherically symmetric model with good NL DSA calculation Tycho efficient DSA No DSA medium eff.

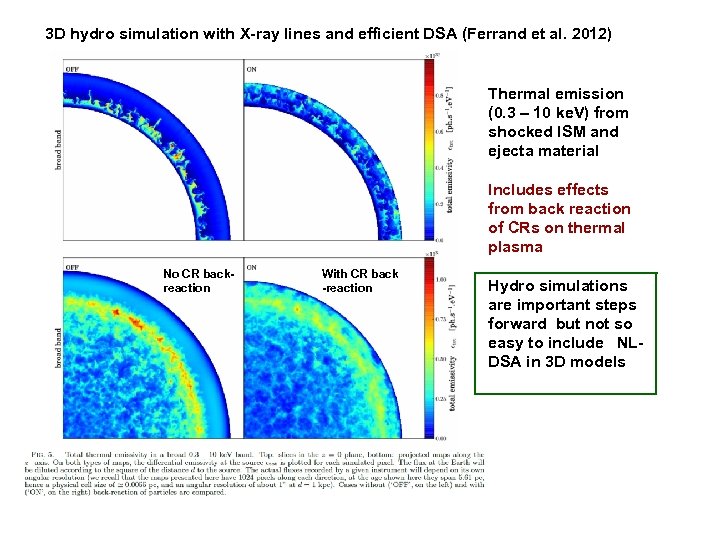3 D hydro simulation with X-ray lines and efficient DSA (Ferrand et al. 2012) Thermal emission (0. 3 – 10 ke. V) from shocked ISM and ejecta material Includes effects from back reaction of CRs on thermal plasma No CR backreaction With CR back -reaction Hydro simulations are important steps forward but not so easy to include NLDSA in 3 D models