The SLAM Project Debugging System Software via Static

The SLAM Project: Debugging System Software via Static Analysis Thomas Ball Sriram K. Rajamani Microsoft Research http: //research. microsoft. com/slam/ 1

2

Thanks To n n n Sagar Chaki (CMU) Satyaki Das (Stanford) Rupak Majumdar (UC Berkeley) Todd Millstein (U. Washington) Robby (KSU) Westley Weimer (UC Berkeley) n Andreas Podelski (MPI) Stefan Schwoon (U. Edinburgh) n Software Productivity Tools Research group at MSR n 3

SLAM Agenda n Overview n Demo n Termination (of SLAM) n Termination (of talk) 4

Specifying and Checking Properties of Programs n Goals n ¨ defect detection ¨ partial validation n ¨automated deduction ¨program analysis ¨type checking ¨model checking Properties safety ¨ temporal safety ¨ security ¨… Many (mature) techniques ¨ memory n Many projects ¨Bandera, ESC-Java, Fea. Ver, JPF, LClint, OSQ, Poly. Scope, PREfix, rccjava, TVLA, Verisoft, Vault, xgcc, … 5

API Usage Rules Programming Testing Code 6

Windows Device Drivers n Kernel presents a very complex interface to driver ¨ stack of drivers ¨ NT kernel multi-threaded ¨ IRP completion, IRQL, plug-n-play, power management, … n Correct API usage described by finite state protocols n Automatically check that clients respect these protocols 7

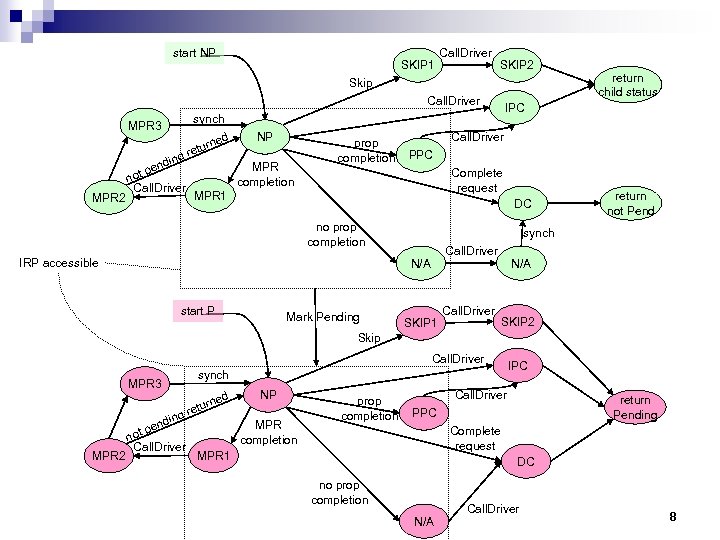
start NP SKIP 1 Call. Driver SKIP 2 Skip Call. Driver d rne tu g re n di pen MPR 2 IPC synch MPR 3 not Call. Driver NP MPR completion prop completion Call. Driver PPC Complete request MPR 1 DC no prop completion IRP accessible Mark Pending return not Pend synch Call. Driver N/A start P return child status SKIP 1 Call. Driver N/A SKIP 2 Skip Call. Driver synch MPR 3 ed ing MPR 2 end ot p n Call. Driver rn retu NP MPR completion prop completion IPC Call. Driver return Pending PPC Complete request MPR 1 DC no prop completion N/A Call. Driver 8

The SLAM Thesis n We can soundly and precisely check a program without annotations against API rules by creating a program abstraction ¨ exploring the abstraction’s state space ¨ refining the abstraction ¨ n We can scale such an approach to many 100 kloc via modular analysis ¨ model checking ¨ 9

SLAM n Input ¨ API usage rules ¨ client C source code n “as is” Analysis ¨ create, explore and refine boolean program abstractions n Output ¨ Error traces (minimize noise) ¨ Verification (soundness) 10

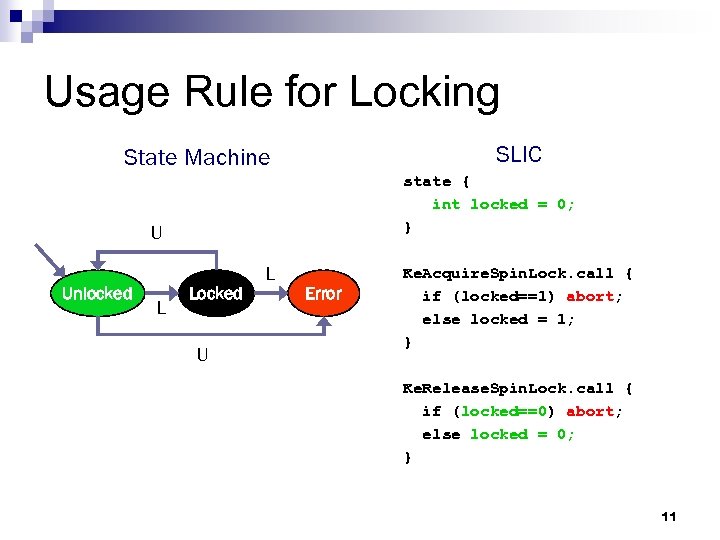
Usage Rule for Locking SLIC State Machine state { int locked = 0; } U Unlocked L Locked U L Error Ke. Acquire. Spin. Lock. call { if (locked==1) abort; else locked = 1; } Ke. Release. Spin. Lock. call { if (locked==0) abort; else locked = 0; } 11

Example do { //get the write lock Ke. Acquire. Spin. Lock(&dev. Ext->write. List. Lock); n. Packets. Old = n. Packets; request = dev. Ext->WLHead. Va; if (request){ Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); . . . n. Packets++; } } while (n. Packets != n. Packets. Old); Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); Loop Invariant: n. Packets = n. Packets. Old IFF lock is held 12

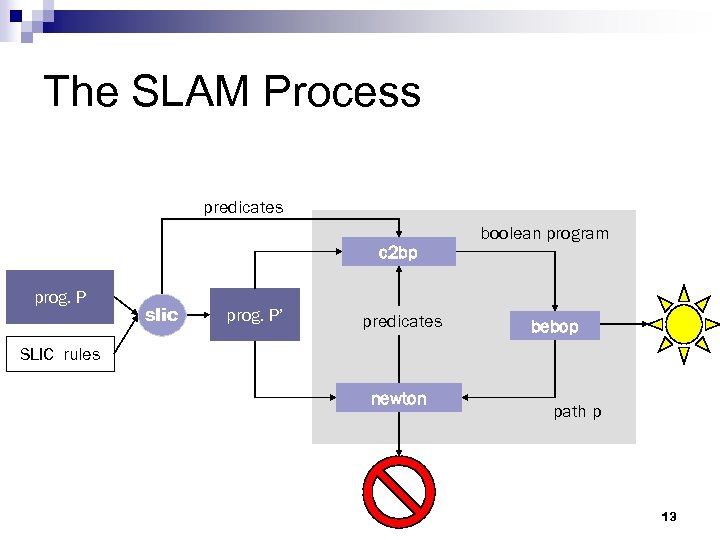
The SLAM Process predicates c 2 bp prog. P slic prog. P’ predicates boolean program bebop SLIC rules newton path p 13

$Instrumented Code do { //get the write lock SLIC_Ke. Acquire. Spin. Lock_call(); Ke. Acquire.$

Instrumented Code do { //get the write lock SLIC_Ke. Acquire. Spin. Lock_call(); Ke. Acquire. Spin. Lock(&dev. Ext->write. List. Lock); n. Packets. Old = n. Packets; request = dev. Ext->WLHead. Va; if (request){ SLIC_Ke. Release. Spin. Lock_call(); Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); . . . n. Packets++; } } while (n. Packets != n. Packets. Old); SLIC_Ke. Release. Spin. Lock_call(); Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); 14

Predicate Abstraction of C (c 2 bp) n Input: a C program P and set of predicates E ¨ predicate n Output: a boolean program bp(P, E) that is ¨a ¨a n = pure C boolean expression sound abstraction of P precise (boolean) abstraction of P Results ¨ separate compilation (predicate abstraction) in presence of procedures and pointers 15

Skeletal Boolean Program do Predicates: //get the write lock SLIC_Ke. Acquire. Spin. Lock_call(); (locked==0) (locked==1) if (*) then SLIC_Ke. Release. Spin. Lock_call(); fi while (*); SLIC_Ke. Release. Spin. Lock_call(); 16

Reachability in Boolean Programs (bebop) n Symbolic interprocedural data flow analysis ¨ Based on CFL-reachability [Reps-Horwitz-Sagiv 95] ¨ Explicit representation of CFG ¨ Implicit representation of reachable states via n BDDs Worst-case complexity is O( P (GL)3 ) ¨ ¨ ¨ P = program size G = number of global states in state machine L = max. number of local states over all procedures 17

Shortest Error Path (Acquire 2 x) Predicates: do //get the write lock SLIC_Ke. Acquire. Spin. Lock_call(); (locked==0) (locked==1) if (*) then SLIC_Ke. Release. Spin. Lock_call(); fi while (*); SLIC_Ke. Release. Spin. Lock_call(); 18

Counterexample-driven Refinement (newton) n Symbolically execute path in C program n Check for path infeasibility at each conditional ¨ Simplify n theorem prover If path is infeasible, generate new predicates to rule out infeasible path ¨ heuristics to generate “weak” explanation 19

Error Path in C code do { //get the write lock Ke. Acquire. Spin. Lock(&dev. Ext->write. List. Lock); n. Packets. Old = n. Packets; request = dev. Ext->WLHead. Va; if (request){ Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); . . . n. Packets++; } } while (n. Packets != n. Packets. Old); Ke. Release. Spin. Lock(&dev. Ext->write. List. Lock); 20

Newton: Path Simulation Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); Conditions: 21

Newton Store: n. Packets = n. Packets. Old; (1) n. Packets. Old: request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); Conditions: 22

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; (1) n. Packets. Old: (2) n. Packets: (1) assume(!request); assume(n. Packets != n. Packets. Old); Conditions: 23

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: assume(!request); assume(n. Packets != n. Packets. Old); Conditions: 24

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: (4) ->WLHead. Va: (3) Conditions: 25

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: (4) ->WLHead. Va: (3) (5) request: (3, 4) Conditions: 26

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: (4) ->WLHead. Va: (3) (5) request: (3, 4) Conditions: ! (5) 27

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: (4) ->WLHead. Va: (3) (5) request: (3, 4) Conditions: ! != (5) (1, 2) 28

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; assume(!request); assume(n. Packets != n. Packets. Old); (1) n. Packets. Old: (2) n. Packets: (1) (3) dev. Ext: (4) ->WLHead. Va: (3) (5) request: (3, 4) Conditions: != (1, 2) 29

Newton Store: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; (1) n. Packets. Old: (2) n. Packets: (1) assume(!request); assume(n. Packets != n. Packets. Old); Conditions: != (1, 2) 30

Newton Predicates: n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; (n. Packets. Old == (n. Packets == ) ) ( != ) assume(!request); assume(n. Packets != n. Packets. Old); 31

Newton n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; Predicates: (n. Packets. Old != n. Packets) assume(!request); assume(n. Packets != n. Packets. Old); 32

Newton n. Packets = n. Packets. Old; request = dev. Ext->WLHead. Va; Predicates: (n. Packets. Old == n. Packets) assume(!request); assume(n. Packets != n. Packets. Old); 33

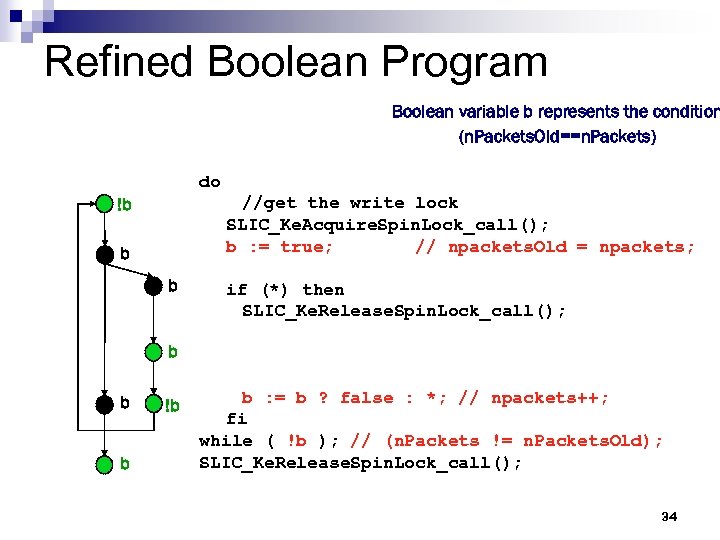
Refined Boolean Program Boolean variable b represents the condition (n. Packets. Old==n. Packets) do //get the write lock SLIC_Ke. Acquire. Spin. Lock_call(); b : = true; // npackets. Old = npackets; !b b b if (*) then SLIC_Ke. Release. Spin. Lock_call(); b b b !b b : = b ? false : *; // npackets++; fi while ( !b ); // (n. Packets != n. Packets. Old); SLIC_Ke. Release. Spin. Lock_call(); 34

Results on Drivers (so far) n Handful of drivers analyzed so far ¨ 2 k-30 k of C code each n Each driver has yielded bugs n SLAM process has always terminated ¨ minutes n to ½ hour Process optimizations have huge effects 35

Demo n Lock example ¨ validation n Lock example with bug ¨ error n trace SLAM’s first bug ¨ floppy device driver 36

Termination of SLAM n [Cousot-Cousot, PLILP’ 92] ¨ widening + abstract interpretation with infinite lattices (WAIL) is more powerful than a (single) finite abstraction n [Ball-Podelski-Rajamani, TACAS’ 02] ¨ finite abstractions plus iterative refinement (FAIR) is more powerful than WAIL 37

Termination and Widening n Widening is used to achieve termination by enlarging the set of states (to reach a fixpoint) ¨ 5 x 10 widened to 5 x n Of course, widening may lose precision n Every fixpoint algorithm that loses precision (in order to terminate) uses widening (implicitly) 38

Fixpoint X : = init; while X S do X’ : = X F(X) if X’ X then break X : = X’ od return X S Fixpoint + Widening (WAIL) X : = init; while X S do X’ : = X F(X) if X’ X then break i : = oracle’s guess X : = W(i, X’) od return X S 39

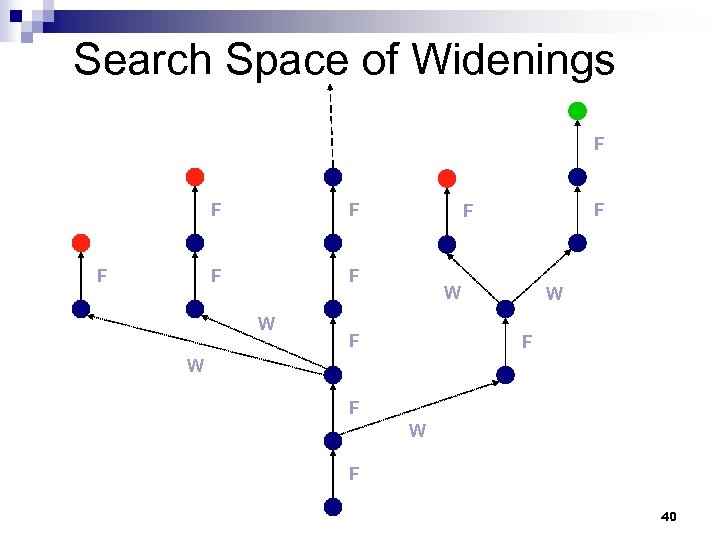
Search Space of Widenings F F F W F W F 40

Finite Abstraction + Iterative Refinement X : = init; while true do P : = atoms(X); X# : = lfp(F#P, init) if X# S then break X : = X F(X) od return X# S n If WAIL succeeds in N iterations then FAIR will succeed in N iterations n But, FAIR can succeed earlier, due to use of interior (abstract) fixpoint 41

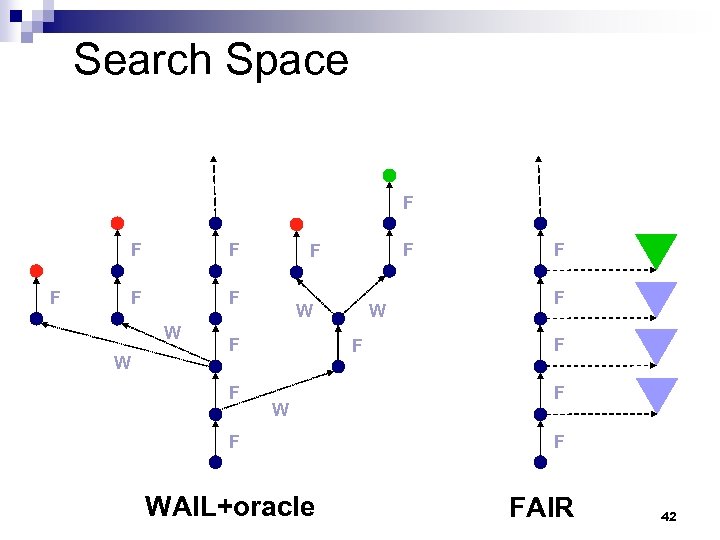
Search Space F F F W W W F F W F WAIL+oracle F F FAIR 42

Searching for Solutions n Once upon a time, only a human could play a great game of chess… ¨… but then smart brute force won the day (Deep Blue vs. Kasparov) n Once upon a time, only a human could design a great abstraction… 43

Termination of Talk n SLAM automatically discovers inductive invariants via ¨ predicate abstraction of C programs ¨ model checking of boolean programs ¨ counterexample-driven refinement n Implemented and starting to yield results on NT device drivers 44

SLAMming on the shoulders of … n Model checking n ¨ predicate abstraction ¨ counterexample-driven refinement ¨ BDDs and symbolic model checking n Program analysis ¨ abstract interpretation ¨ points-to analysis ¨ dataflow via CFL- Automated deduction ¨ weakest ¨ theorem n preconditions proving Software ¨ AST toolkit ¨ Das’s Golf ¨ CU and CMU BDD ¨ Simplify, Vampyre ¨ OCAML reachability 45

SLAM Future Work n More impact ¨ Static n Driver Verifier (internal, external) More features ¨ Heap abstractions ¨ Concurrency n More languages ¨ C# n and CIL More users ¨ 2002 public release of SLAM toolkit 46

Predictions n The holy grail of full program verification has been abandoned n New checking tools will emerge and be widely used n Tools will ¨ exploit ideas from various analysis disciplines ¨ alleviate the “chicken-and-egg” problem of specifications 47

Challenges / SLAM Reading List n Specifications ¨ Mining n specifications Abstractions ¨ Predicate n abstraction for software verification Annotations ¨ Types as models: ¨ Role analysis n Soundness ¨ Ccured: n model checking MP programs type-safe retrofitting of legacy code Scaling ¨ Lazy abstraction 48

The End 49