0725180fe38b6c578a78e4c01ddcfb35.ppt
- Количество слайдов: 55

The Seventh International Conference on Vibration Problems Dynamics of Networks with Bistable Links Andrej Cherkaev, Elena Cherkaev Department of Mathematics, University of Utah, USA and Leonid Slepyan Department of Solid Mechanics, Materials and Structures, Tel Aviv University, Israel IPME, s. Pb, November 2007

Acknowledgements The talk is partly based on the joint results obtained in collaboration with the fellows of Department of Mathematics, University of Utah Professor Alexander Balk, Ph. D student Seubpong Leelavanishkul, Assistant Research Professor Alexander Vinogradov, Assistant Research Professor Toshio Yoshikawa, Assistant Research Professor Liya Zhornitzkaya. The project is supported by ARO and NSF IPME, s. Pb, November 2007

Motivation: Find a structure that can withstand a dynamic impact IPME, s. Pb, November 2007

Outline • • • Waiting links and structures from them Waves of damage Smart structures from bistable links Dynamics of invertible phase transition Spontaneous waves Dynamic homogenization IPME, s. Pb, November 2007

Situation: A relatively slow and massive projectile collides with the structure. (“slow” compared to the speed of sound in the material, appox. 3000 m/sec for steel) Observe that The material itself can absorb he energy and resist until it melts Failure is caused by stress localization: Most of the material stays undamaged after the structure fails! Aim: delocalize the stress and stabilize the failure IPME, s. Pb, November 2007

Tao of Damage Tao -- the process of nature by which all things change and which is to be followed for a life of harmony. Webster o Damage happens! o Dispersed damage absorbs energy; concentrated damage destroys. o Design is the Art of Damage Scattering IPME, s. Pb, November 2007

Means of Delocalization The propagation of “partial damage” can be achieved by using chains and lattices from locally unstable cells --waiting links -- with reserved capacity to resistance (Ch, Slepyan, 1998) The waiting links structures excite waves of partial damage that effectively dissipate and radiate the energy of an impact IPME, s. Pb, November 2007

Elastic-brittle material (limited strength) • The force-versus-elongation relation in a monotonically elongated bar from elastic-brittle material is • Accounting for the prehistory, we obtain the relation c(x, t) is the damage parameter IPME, s. Pb, November 2007

Waiting links • • • Consists of two “parallel” rods; one is slightly longer. The second (slack) rod starts to resist when the elongation is large enough. Waiting links allow for inner instability and increase the interval of nondestuctive (nonfatal) deformations. c is the damage parameter IPME, s. Pb, November 2007

Chain of rods • Several elements form a chain What happens when the chain is elongated? Multiple breakings occur and “Partial damage” propagates along the rod. IPME, s. Pb, November 2007

Quasistatic state and the energy Force Elongation Breaks of basic links Final break The chain behaves as a superplastic material. The absorbed energy Ew is proportional to the number of “partially damaged” links; The chain absorbs more energy before total breakage than a single rod of the combined thickness; IPME, s. Pb, November 2007

Waves in waiting-link structures Why study them? • Breakages transform the energy of a slow impact to energy of intensive waves. • Waves radiate and dissipate the energy and carry it away from the zone of contact. • At the other hand, waves localize the energy that may damage or destroy the link. After: L. Slepyan, A. Cherkaev, E. Cherkaev. JPMS 2004. Part 1 IPME, s. Pb, November 2007

Effectiveness of waiting links IPME, s. Pb, November 2007

Simulation A large slow-moving mass (7% of the speed of sound) is attached to one end of the chain, the other end is fixed. During the simulation, the mass of the projectile M was increased until the chain was broken. Constitutive relation in links a is the fraction of material used in the forerun “basic” link IPME, s. Pb, November 2007

Results Efficiency: 750/150=5 a=1 (no waiting links) M = 150 M=375, a=0. 25 IPME, s. Pb, November 2007 M=700 a=. 25 Small dissipation M=750 a=. 25 Small dissipation

Effectiveness of structure resistance To measure the effectiveness, we use • the ratio R of the momentum of the projectile after and before the impact. This parameter is independent of the type of structural damage. Collision R • propagation 1 rejection absorption -1 v(0) v(T) 0 The minimal mass M that breaks the chain moving with a fixed speed. Both parameters are proportional to the volume of a chain with waiting links, not to its crossection. IPME, s. Pb, November 2007

Theory: Wave of transition in infinite chains Analytic description and the speed of propagation. L. Slepyan, A. Cherkaev, E. Cherkaev. JPMS 2004 Part 11 IPME, s. Pb, November 2007

Use of a linear theory for description of nonlinear chains The force in the nonlinear link is viewed as a linear response to the elongation plus an additional external pair of forces, applied in the proper time when the elongation reaches the critical value. Trick (Slepyan and Troyankina, 1988): Model the jump in resistance by an action of an external pair of forces Force Elongation Before damage (transition) IPME, s. Pb, November 2007 After damage (transition)

Equations of chain dynamics Dynamics is described by an infinite system of nonlinear equations with coefficients that are discontinuous trigger-type functions of the solution Can we integrate it? Yes (in some cases)! IPME, s. Pb, November 2007

Generally, the approach is as follows: A nonlinear system of DE of the type where L is a linear diff. operator, H is the Heaviside function is equivalently replaced by a system of linear inhomogeneous DE where the instances are defined from an additional nonlinear algebraic conditions (turn-on – turn-off conditions) IPME, s. Pb, November 2007

Wave motion: Ansatz • • • Boundary conditions: constant speed at the infinitely distant left end, constant pressure at the infinitely distant right end. The wave propagates with a constant but unknown speed v Therefore, the introduced “pairs of forces” are applied at equally-distanced instances. Motion of masses is self-similar The ansatz reduces the problem to a problem about a wave in a linear chain caused by running pairs of forces applied to its links. IPME, s. Pb, November 2007

Scheme of solution 1. The equation for the zero-numbered mass is 2. The Fourier transform of it is where 3. Return to originals, 4. Find the unknown speed from the closing nonlinear eq: IPME, s. Pb, November 2007

Additional considerations 1. One needs to separate waves originated by breakage from other possible waves in the linear system. For this, we use the “causality principle” (Slepyan) of the viscous solution technique. 2. The solution is more complicated when the elastic properties are switched after the transition. In this case, the Wiener-Hopf technique is applied. 3. In finite networks, the reflection of the wave is critical since the magnitude doubles. IPME, s. Pb, November 2007
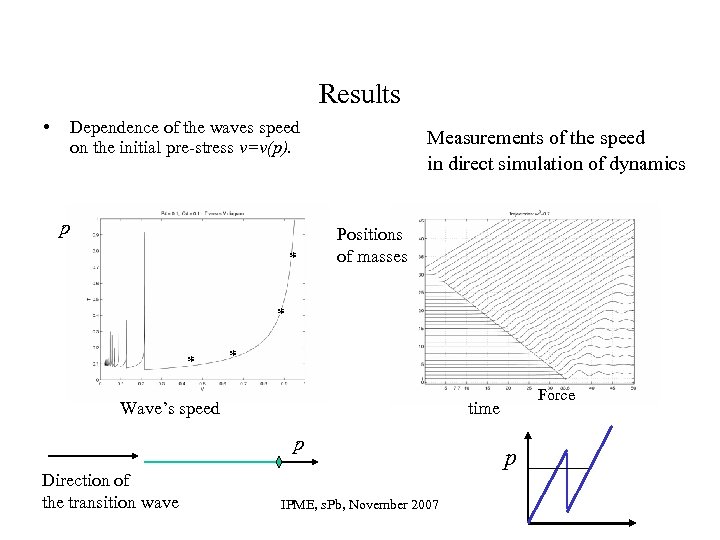
Results • Dependence of the waves speed on the initial pre-stress v=v(p). p * Measurements of the speed in direct simulation of dynamics Positions of masses * * * Wave’s speed time p Direction of the transition wave Force IPME, s. Pb, November 2007 p

Discussion • The domino problem: Will the wave of transiton propagate? The propagation of the wave is contingent on its accidental initiation. • 2 D model: Similarity between crack propagation and the plane waves of transition (Slepyan IMPS, 2003) • Homogenization: The speed of the wave can be found from atomistic model, as a function of stress. IPME, s. Pb, November 2007

Spread of damage as phase transition Chain model allows to find (i) Condition for wave initiation (ii) Speed of phase transition (iii) Magnitude: max{u(x, t)} The right-hand side of is a bistable function; equilibrium is nonunique. IPME, s. Pb, November 2007

Lattices with waiting links Smart structures from bistable elements IPME, s. Pb, November 2007

Green’s function for a damaged lattice: Statics The lattice with waiting links is described in the same manner. The damage in a link is mimicked by an applied pair of forces F(k, m, Green’s function: Influence of one damaged link: N’ N IPME, s. Pb, November 2007 N, N’)
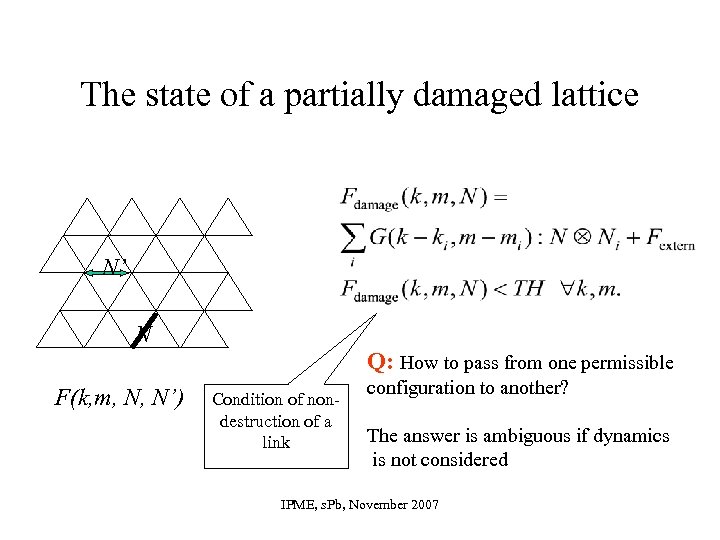
The state of a partially damaged lattice N’ N Q: How to pass from one permissible F(k, m, N, N’) Condition of nondestruction of a link configuration to another? The answer is ambiguous if dynamics is not considered IPME, s. Pb, November 2007

Unstrained damaged configurations • Generally, damage propagates like a crack due to local stress concentration. • The expanded configurations are not unique. • There are exceptional unstrained configurations which are the attraction points of the damage dynamics and the null-space of F. IPME, s. Pb, November 2007

Set of unstrained configurations • The geometrical problem of description of all possible unstrained configuration is still unsolved. • Some sophisticated configurations can be found. • Because of nonuniqueness, the growth of damage problem requires dynamic consideration. Random lattices: Nothing known IPME, s. Pb, November 2007
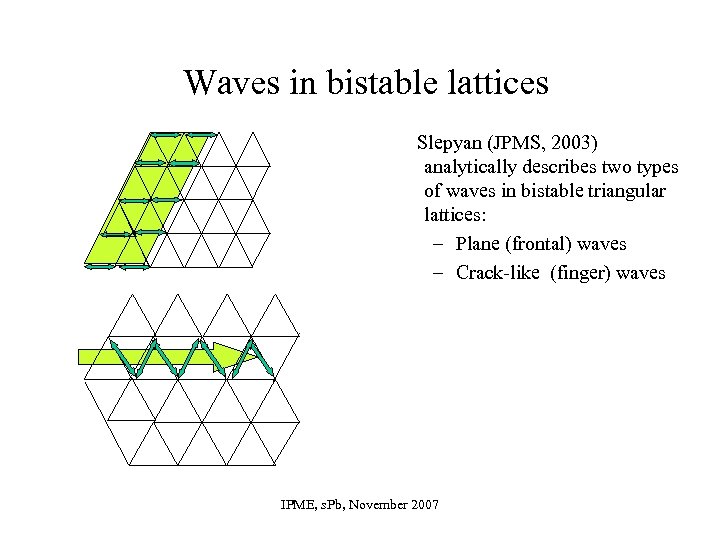
Waves in bistable lattices Slepyan (JPMS, 2003) analytically describes two types of waves in bistable triangular lattices: – Plane (frontal) waves – Crack-like (finger) waves IPME, s. Pb, November 2007

Conservative bistable system IPME, s. Pb, November 2007
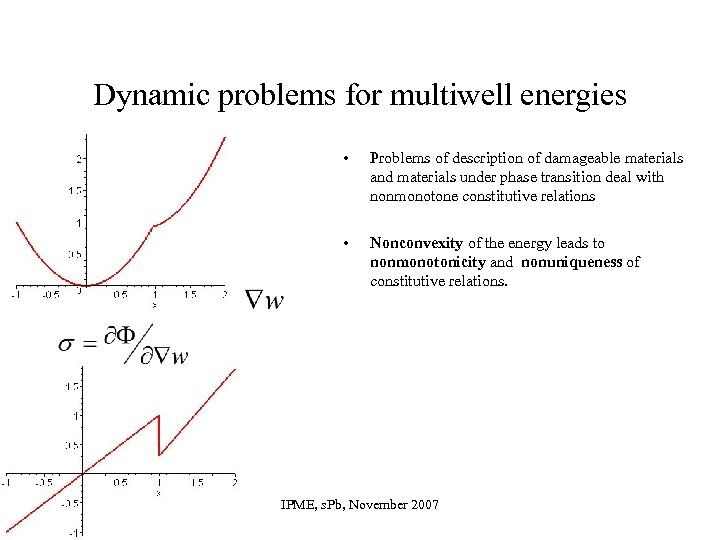
Dynamic problems for multiwell energies • Problems of description of damageable materials and materials under phase transition deal with nonmonotone constitutive relations • Nonconvexity of the energy leads to nonmonotonicity and nonuniqueness of constitutive relations. IPME, s. Pb, November 2007
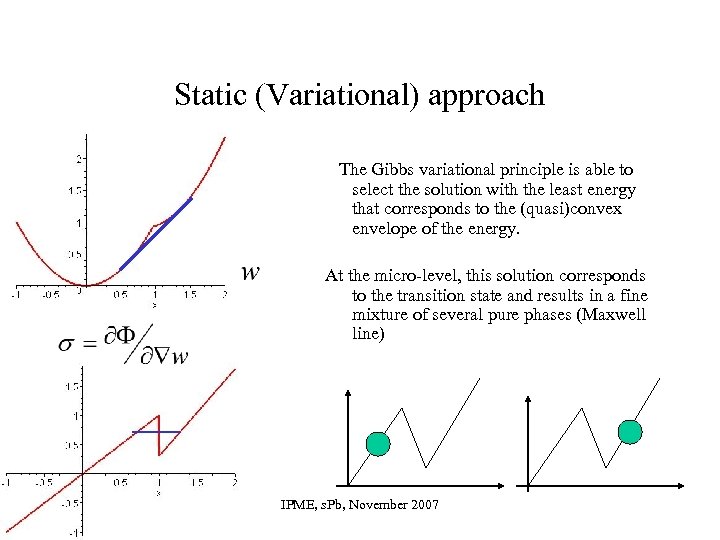
Static (Variational) approach The Gibbs variational principle is able to select the solution with the least energy that corresponds to the (quasi)convex envelope of the energy. At the micro-level, this solution corresponds to the transition state and results in a fine mixture of several pure phases (Maxwell line) IPME, s. Pb, November 2007

Dynamic problems for multiwell energies • Formulation: Lagrangian for a continuous medium If W is (quasi)convex • If W is not quasiconvex • Radiation and other losses Questions: – – – Dynamic There are many local minima; each corresponds to an equilibrium. homogenization How to distinguish them? The realization of a particular local minimum depends on the existence of a path to it. What are initial conditions that lead to a particular local minimum? How to account for dissipation and radiation? IPME, s. Pb, November 2007

Paradoxes of relaxation of an energy by a (quasi)convex envelope. • To move along the surface of minimal energy, the particles must: – Sensor the proper instance of jump over the barrier – Borrow somewhere an additional energy, store it, and use it to jump over the barrier – Get to rest at the new position, and return the energy I suddenly feel that now it is the time to leave my locally stable position! Thanks for the energy! I needed it to get over the barrier. What a roller coaster! Energy bank IPME, s. Pb, November 2007 Stop right here! Break! Here is your energy. Take it back. Energy bank
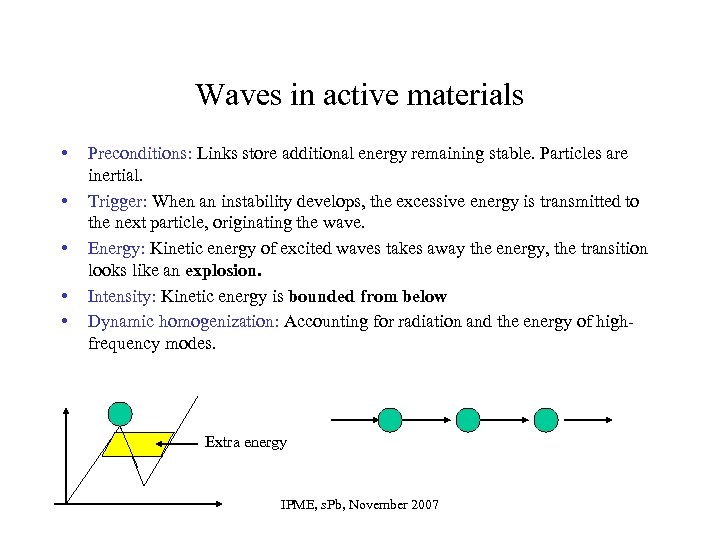
Waves in active materials • • • Preconditions: Links store additional energy remaining stable. Particles are inertial. Trigger: When an instability develops, the excessive energy is transmitted to the next particle, originating the wave. Energy: Kinetic energy of excited waves takes away the energy, the transition looks like an explosion. Intensity: Kinetic energy is bounded from below Dynamic homogenization: Accounting for radiation and the energy of highfrequency modes. Extra energy IPME, s. Pb, November 2007

Dynamics of chains from bi-stable elements (exciters) with Alexander Balk, Leonid Slepyan, and Toshio Yoshikawa A. Balk, A. Cherkaev, L. Slepyan 2000. IJPMS T. Yoshikawa, 2002, submitted IPME, s. Pb, November 2007

Unstable reversible links Force • • • Each link consists of two parallel elastic rods, one of which is longer. Initially, only the longer road resists the load. If the load is larger than a critical (buckling)value: Elongation ü The longer bar looses stability (buckling), and ü the shorter bar assumes the load. The process is reversible. H is the Heaviside function No parameters! IPME, s. Pb, November 2007

Chain dynamics. Generation of a spontaneous transition wave x 0 f(z) Initial position: z linear regime (N=0), but close to the critical point of transition IPME, s. Pb, November 2007

Observed spontaneous waves in a chain “Twinkling” phase “Chaotic” phase Under a smooth excitation, the chain develops intensive oscillations and waves. Sonic wave Wave of phase transition IPME, s. Pb, November 2007

“Twinkling” phase and Wave of phase transition (Small time scale) After the wave of transition, the chain transit to a new twinkling (or headed) state. We find global (homogenized) parameters of transition: ü ü Speed of the wave of phase transition “Swelling” parameter Period Phase shift IPME, s. Pb, November 2007

Periodic waves: Analytic integration Approach, after Slepyan and Troyankina Nonlinearities are replaced by a periodic external forces; period is unknown Self-similarity Periodicity System (*) can be integrated by means of Fourier series. A single nonlinear algebraic equation defines the instance q. IPME, s. Pb, November 2007

1. Stationary waves Use of the piece-wise linearity of the system of ODE and the above assumptions The system is integrated as a linear system (using the Fourier transform), then the nonlinear algebraic equation for the unknown instances q of the application/release of the applied forces is solved. Result: The dispersion relation IPME, s. Pb, November 2007

2. Waves excited by a point source For the wave of phase transition we assume that k-th mass enters the twinkling phase after k periods The self-similarity assumption is weakened. Asymptotic periodicity is requested. IPME, s. Pb, November 2007

Large time range description with Toshio Yoshikawa IPME, s. Pb, November 2007

Problem of homogenization of a dynamic system Consider a chain, fixed at the lower end and is attached by a “heavy” mass M=3, 000 m at the top. T >> 1/M, M >>m Problem: Approximate the motion of the mass M by a single differential equation Find IPME, s. Pb, November 2007
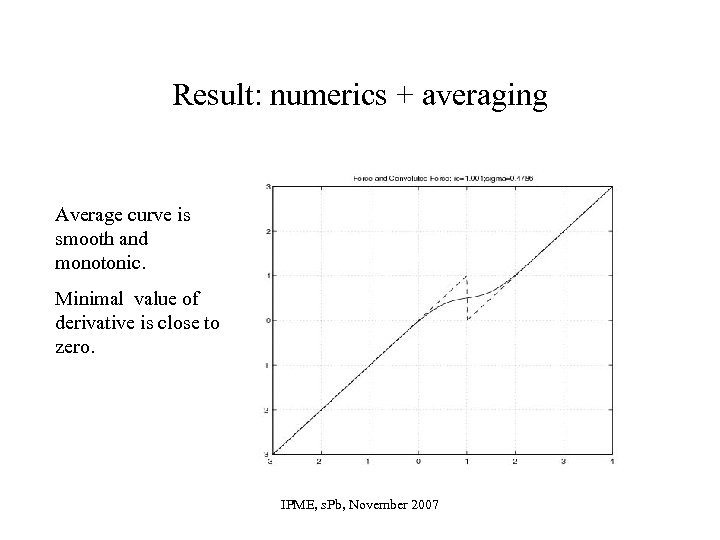
Result: numerics + averaging Average curve is smooth and monotonic. Minimal value of derivative is close to zero. IPME, s. Pb, November 2007

Homogenized constitutive relation (probabilistic approach) f Coordinate of the “large mass” is the sum of elongations of many nonconvex springs that (as we have checked by numerical experiments) are almost uncorrelated, (the correlation decays exponentially, ) while the time average of the force is the same in all springs: The dispersion is of the order of the hollow in the nonconvex constitutive relation. IPME, s. Pb, November 2007

Add a small dissipation: Continuous limit is very different: The force becomes The system demonstrates a strong hysteresis. IPME, s. Pb, November 2007

Homogenized model (with dissipation) Broken barrier • v • Tension bed Small magnitude: Linear elastic material Larger magnitude: Highly dissipative nonlinear material. IPME, s. Pb, November 2007 Initiation of vibration is modeled by the break of a barrier each time when the unstable zone is entered. Dissipation is modeled by tension in the unstable zone.

Energy path Initial energy The magnitude of the high-frequency mode is bounded from below Energy of High-frequency high-frequency vibrations: Slow motion Dissipation IPME, s. Pb, November 2007

Method of dynamic homogenization • We are investigating mass-spring chains and lattices, which allows to – account for concentrated events as breakage – describe the basic mechanics of transition – compute the speed of phase transition. • The atomic system is strongly nonlinear but can be piece-wise linear. • To obtain the macro-level description, we – analyze the solutions of this nonlinear system at micro-level – homogenize these solutions, – derive the consistent equations for a homogenized system. IPME, s. Pb, November 2007

Thank you for your attention IPME, s. Pb, November 2007
0725180fe38b6c578a78e4c01ddcfb35.ppt