The Rule of 72 The most important and

The Rule of 72 The most important and simple rule to financial success. © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

Simply put 72 Is a Magical Number © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona 1. 14. 3. G 1

What is the rule of 72? It can tell you: 1) 2) 3) 4) 1. 14. 3. G 1 How many years it will take an investment to double at a given interest rate using compounding interest. How long it will take debt to double if no payments are made. The interest rate an investment must earn to double within a specific time period. How many times money (or debt) will double in a specific time period. © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 1) How long will it take for our investment to double p When 72 is divided by the interest rate, the answer is the number of years it will take the investment to double. EXAMPLE: We know our interest rate is 10% on our investment. TO FIGURE THIS: 72 ÷ 10 = 7. 2 YEARS TO DOUBLE © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 ANOTHER EXAMPLE: Compound Interest is 8% p How long will it take for the investment to double? p 72 divided by 8% = 9 years At the end of nine years, the initial savings of $100 will have increased to $200 — which is double the amount of initial savings © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 How long it will take debt to double if no payments are made p You borrow $1, 000 from a friend, who is charging 6% interest. If you do NOT make ANY payments, how long will it take for your debt to double? 72 ÷ 6 = 12 YEARS FOR DEBT TO DOUBLE © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 The interest rate an investment must earn to double within a specific time period p If a person would like his/her investment to double in 4 years, you would calculate it like this – 72 ÷ 4 = 18% interest rate is required on the investment ANOTHER EXAMPLE: Would like investment to double in 6 years Need 12% interest rate investment to double in 6 years for © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

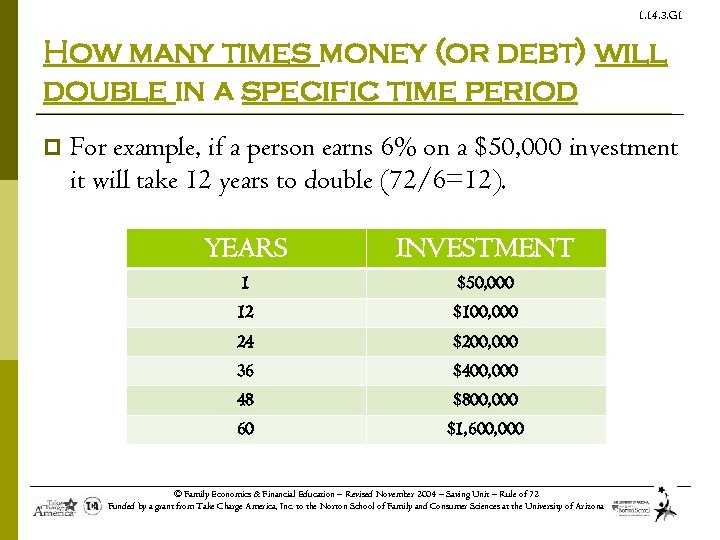1. 14. 3. G 1 How many times money (or debt) will double in a specific time period p For example, if a person earns 6% on a $50, 000 investment it will take 12 years to double (72/6=12). YEARS INVESTMENT 1 $50, 000 12 $100, 000 24 $200, 000 36 $400, 000 48 $800, 000 60 $1, 600, 000 © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 You must remember a few things about the “Rule of 72” The “Rule of 72” p Is only an approximation p The interest rate must remain constant p The equation does not allow for additional payments to be made to the original amount p Interest earned is reinvested p Tax deductions are not included within the equation © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 ? ? ? ? ? ? ? Where did the Rule of 72 come from? © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Albert Einstein Credited for discovering the mathematical equation for compounding interest, thus the “Rule of 72” T=P(I+I/N)YN “It is the greatest mathematical discovery of all time. ” *(Notes below) © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Albert Einstein discovered this simple equation for compounding interest that allows people to easily understand the time value of money. Time Value of Money is a calculation that adjusts for the fact that dollars to be received or paid out in the future are not equivalent to those received or paid out today because of compounding interest. © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 REVIEW OF RULE OF 72 © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 WHAT IS COMPOUNDING INTEREST Compounding interest is Interest earning interest on interest! © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

Nathan’s Certificate of Deposit 1. 14. 3. G 1 Nathan invested $2, 500 into a Certificate of Deposit earning a 6. 5% interest rate. How long will it take Nathan’s investment to double? p Invested $2, 500 p Interest Rate is 6. 5% 72 = 11 years to double investment 6. 5% © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Another Example The average stock market return since 1926 has been 11% 72 11% = 6. 5 years to double investment Therefore, every 6. 5 years an individual’s investment in the stock market has doubled © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Jessica’s Credit Card Debt Jessica has a $2, 200 balance on her credit card with an 18% interest rate. If Jessica chooses to not make any payments and does not receive late charges, how long will it take for her balance to double? $2, 200 balance on credit card p 18% interest rate p 72 18% = 4 years to double debt © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

Another Example: How long will it take for debt to double? $6, 000 balance on credit card p 22% interest rate p 72 22% = 3. 3 years to double debt © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona 1. 14. 3. G 1

1. 14. 3. G 1 Jacob’s Car Jacob currently has $5, 000 to invest in a car after graduation in 4 years. What interest rate is required for him to double his investment? p $5, 000 to invest p Wants investment to double in 4 years 72 4 years = 18% interest rate © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Another Example $3, 000 to invest p Wants investment to double in 10 years p 72 10 years = 7. 2% interest rate © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Rhonda’s Treasury Note Rhonda is 22 years old and would like to invest $2, 500 into a U. S. Treasury Note earning 7. 5% interest. How many times will Rhonda’s investment double before she withdraws it at age 70? Age 22 31. 6 41. 2 72 = 9. 6 years 7. 5% to double investment Investment $2, 500 $5, 000 $10, 000 50. 8 60. 4 70 $20, 000 $40, 000 $80, 000 © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

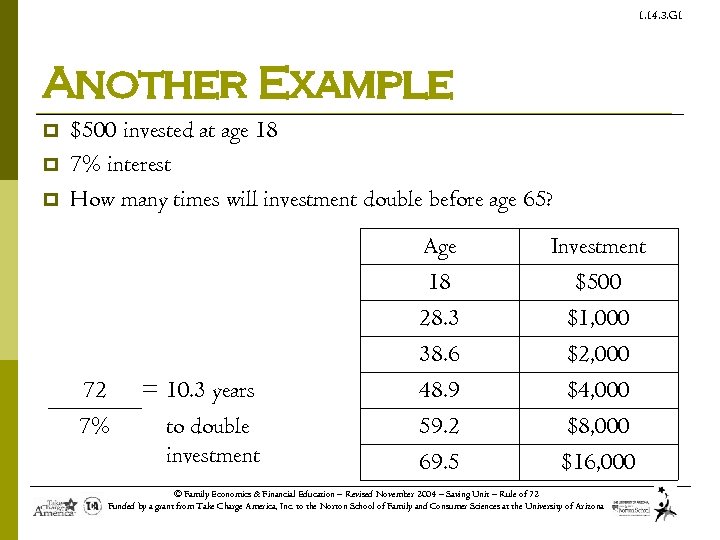1. 14. 3. G 1 Another Example p p p $500 invested at age 18 7% interest How many times will investment double before age 65? Age 18 28. 3 38. 6 72 7% = 10. 3 years to double investment Investment $500 $1, 000 $2, 000 48. 9 59. 2 69. 5 $4, 000 $8, 000 $16, 000 © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 THE END © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Taxes A person can choose to invest into two types of accounts: p Taxable Account – taxes charged to earned interest p Tax Deferred Account – taxes are not paid until the individual withdraws the money from the investment © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Taxes Example George is in the 33% tax bracket. He would like to invest $100, 000. George is comparing two accounts that have a 6% interest rate. The first is a taxable account charging interest earned. The second account is tax deferred until he withdraws the money. Which account should George invest his money into? © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

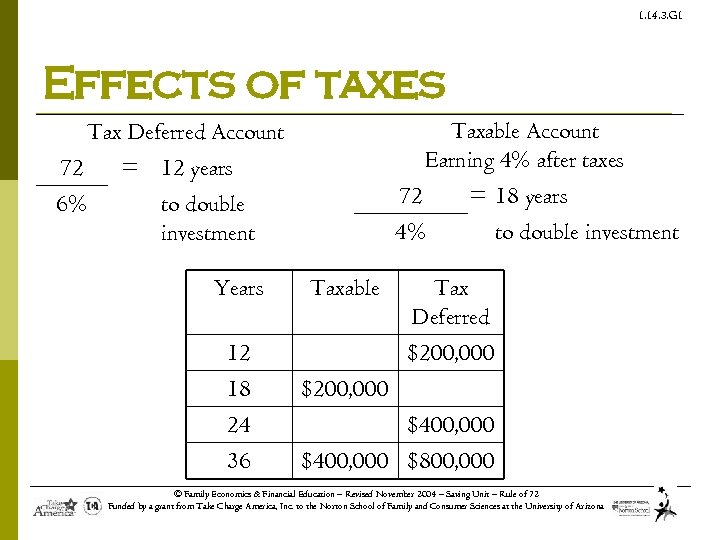1. 14. 3. G 1 Effects of taxes Taxable Account Earning 4% after taxes Tax Deferred Account 72 = 12 years 6% to double investment Years 12 18 24 36 72 = 18 years 4% Taxable to double investment Tax Deferred $200, 000 $400, 000 $800, 000 © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Conclusion p The Rule of 72 can tell a person: n n How many years it will take an investment to double at a given interest rate using compounding interest; How long it will take debt to double if no payments are made; The interest rate an investment must earn to double within a specific time period; How many times money (or debt) will double in a specific time period. © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 Conclusion continued p Things individuals must remember about the Rule of 72 include: n n n Is only an approximation The interest rate must remain constant The equation does not allow for additional payments to be made to the original amount Interest earned is reinvested Tax deductions are not included within the equation © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona

1. 14. 3. G 1 ASSIGNMENT - Rule of 72 Worksheet (1. 14. 3. A 1) Rule of 72 Math (front & back) Compounding Interest Quarterly © Family Economics & Financial Education – Revised November 2004 – Saving Unit – Rule of 72 Funded by a grant from Take Charge America, Inc. to the Norton School of Family and Consumer Sciences at the University of Arizona