The role of probability in statistics In statistical

The role of probability in statistics In statistical inference, we want to make general statements about the population based on measurements taken from a sample. How will all suspension systems produced with the new composite behave? How will the radar navigation system perform in all aircraft? What speed improvements will we obtain for all roofing applications using the new product? To answer these questions, we ______ from the population and hope to generalize the results. 1 ETM 620 - 09 U

Probability See chapter 1 of Hines et al. for more The probability of an event, A is the likelihood of that event given the entire sample space of possible events. 0 ≤ P(A) ≤ 1 P(ø) = 0 P(S) = 1 For mutually exclusive events, P(A 1 U A 2 U … U Ak) = P(A 1) + P(A 2) + … P(Ak) 2 ETM 620 - 09 U

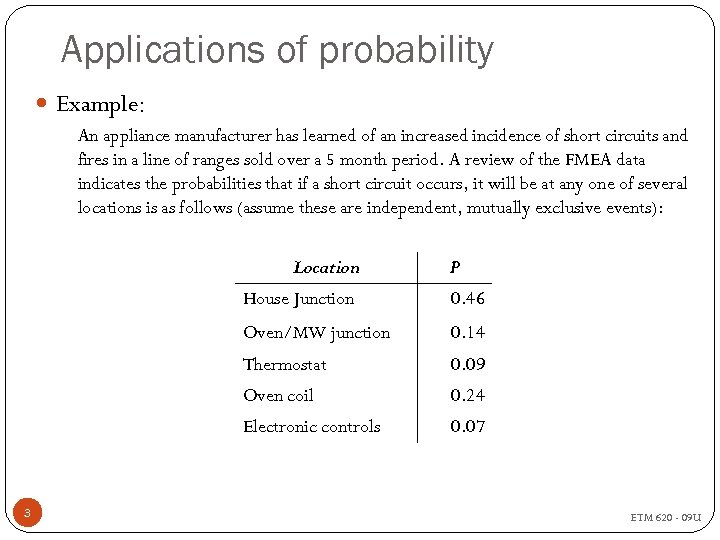
Applications of probability Example: An appliance manufacturer has learned of an increased incidence of short circuits and fires in a line of ranges sold over a 5 month period. A review of the FMEA data indicates the probabilities that if a short circuit occurs, it will be at any one of several locations is as follows (assume these are independent, mutually exclusive events): Location P House Junction Oven/MW junction 0. 14 Thermostat 0. 09 Oven coil 0. 24 Electronic controls 3 0. 46 0. 07 ETM 620 - 09 U

Applications of probability The probability that the short circuit does not occur at the house junction is … The probability that the short circuit occurs at either the Oven/MW junction or the oven coil is … The probability that both the electronic controls and thermostat short circuit simultaneously is … 4 ETM 620 - 09 U

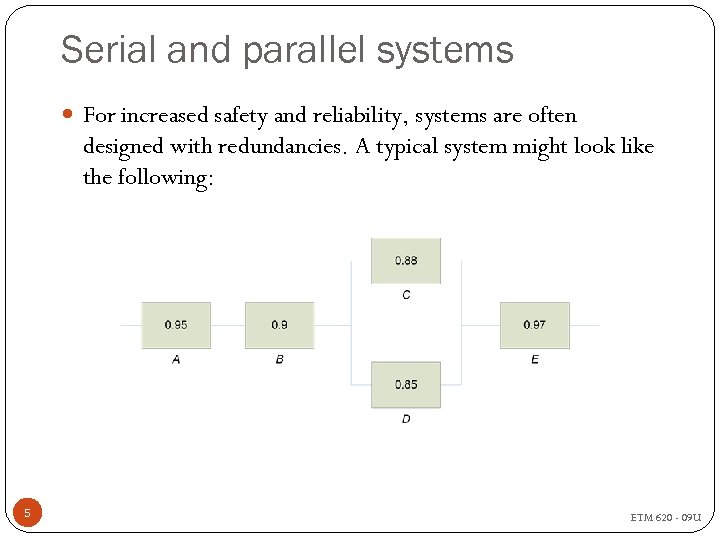
Serial and parallel systems For increased safety and reliability, systems are often designed with redundancies. A typical system might look like the following: 5 ETM 620 - 09 U

Serial and parallel systems What is the probability that: Segment 1 works? 1 2 Segment 2 works? The entire system works? 6 ETM 620 - 09 U

Conditional probability If segment 2 works, what is the probability that component C does not work? 7 ETM 620 - 09 U

Conditional probability If the system works, what is the probability that component D does not work? 8 ETM 620 - 09 U

Defining probabilities: Random variables To learn more, refer to chapter 2 of Hines et al. Examples: Out of 100 heart catheterization procedures performed at a local hospital each year, the probability that more than five of them will result in complications is _____ Drywall anchors are sold in packs of 50 at the local hardware store. The probability that no more than 3 will be defective is _____ In general, ______ 9 ETM 620 - 09 U

Functions of random variables Chapter 3 of Hines et al. Example: Probability of X, the number of cars passing through a car wash in one hour on a sunny Friday afternoon, is given by x P(X = x) 4 5 1/12 6 7 8 9 1/4 1/6 Let g(X) = 2 X -1 represent the amount of money paid to the attendant by the manager. What can the attendant expect to earn during this hour on any given sunny Friday afternoon? E[g(X)] = Σ g(x) f(x) = __________ 10 = ________________ ETM 620 - 09 U

Mathematical expectation Example: Repair costs for a particular machine are represented by the following probability distribution: x $50 200 350 P(X = x) 0. 3 0. 2 0. 5 What is the expected value of the repairs? – That is, over time what do we expect repairs to cost on average? 11 ETM 620 - 09 U

Expected value μ = E(X) μ = mean of the probability distribution For discrete variables, μ = E(X) = ∑ x f(x) So, for our example, E(X) = ____________ 12 ETM 620 - 09 U

Your turn … By investing in a particular stock, a person can take a profit in a given year of $4000 with a probability of 0. 3 or take a loss of $1000 with a probability of 0. 7. What is the investor’s expected gain on the stock? 13 ETM 620 - 09 U

Variability Recall our example: Repair costs for a particular machine are represented by the following probability distribution: x $50 200 350 P(X = x) 0. 3 0. 2 0. 5 What is the variance in the repair cost? – That is, how might we define the spread of costs? 14 ETM 620 - 09 U

Variance Remember § μ = E(X) = $230 Then, for discrete variables, σ2 = E [(X - μ)2] = ∑ (x - μ)2 f(x) = E (X 2) - μ 2 So, for our example, σ2 = ____________ 15 ETM 620 - 09 U

Your turn … By investing in a particular stock, a person can take a profit in a given year of $4000 with a probability of 0. 3 or take a loss of $1000 with a probability of 0. 7. What are the variance and standard deviation of the investor’s gain on the stock? 16 ETM 620 - 09 U

Known probability distributions Engineers frequently work with data that can be modeled as one of several known probability distributions. Being able to model the data allows us to: model real systems design predict results Key discrete probability distributions (Chapter 5) include: binomial negative binomial (incl. Pascal) hypergeometric Poisson 17 ETM 620 - 09 U

Bernoulli trials Examples: Inspect tires coming off the production line. Classify each as defective or not defective. Define “success” as defective. If historical data shows that 95% of all tires are defect-free, then P(“success”) = 0. 05. Signals picked up at a communications site are either incoming speech signals or “noise. ” Define “success” as the presence of speech. P(“success”) = P(“speech”) Administer a test drug to a group of patients with a specific condition. P(“success”) = ______ Bernoulli Process n repeated trials the outcome may be classified as “success” or “failure” the probability of success (p) is constant from trial to trial repeated trials are independent. 18 ETM 620 - 09 U

Binomial distribution Example: Historical data indicates that 10% of all bits transmitted through a digital transmission channel are received in error. Let X = the number of bits in error in the next 4 bits transmitted. Assume that the transmission trials are independent. What is the probability that Exactly 2 of the bits are in error? At most 2 of the 4 bits are in error? more than 2 of the 4 bits are in error? The number of successes, X, in n Bernoulli trials is called a binomial random variable. 19 ETM 620 - 09 U

Binomial distribution The probability distribution is called the binomial distribution. b(x; n, p) = where , x = 0, 1, 2, …, n p = _________ q = _________ For our example, b(x; n, p) = _________ 20 ETM 620 - 09 U

For our example … What is the probability that exactly 2 of the bits are in error? At most 2 of the 4 bits are in error? 21 ETM 620 - 09 U

Your turn … What is the probability that more than 2 of the 4 bits are in error? 22 ETM 620 - 09 U

Expectations of the binomial distribution The mean and variance of the binomial distribution are given by µ = np σ 2 = npq Suppose, in our example, we check the next 20 bits. What are the expected number of bits in error? What is the standard deviation? μ = ______ σ 2 = _____ , σ = _____ 23 ETM 620 - 09 U

Another example A worn machine tool produces 1% defective parts. If we assume that parts produced are independent, what is the mean number of defective parts that would be expected if we inspect 25 parts? What is the expected variance of the 25 parts? 24 ETM 620 - 09 U

Helpful hints … Sometimes it helps to draw a picture. Suppose we inspect the next 5 parts … P(at least 3) P(2 ≤ X ≤ 4) P(less than 4) In Excel, the function =binomdist(number_s, trials, probability_s, cumulative) gives the cumulative distribution function (when cumulative = “true” or 1) and the probability mass function (when cumulative = “false” or 0). 25 ETM 620 - 09 U

Multinomial experiments What if there are more than 2 possible outcomes? (e. g. , acceptable, scrap, rework) That is, suppose we have: n independent trials k outcomes that are mutually exclusive (e. g. , ♠, ♣, ♥, ♦) exhaustive (i. e. , ∑all k pi = 1) Then f(x 1, x 2, …, xk; p 1, p 2, …, pk, n) = 26 ETM 620 - 09 U

Example According to genetic theory, a certain cross of guinea pig will result in red, black, and white offspring in the ratio 8: 4: 4. What is the probability that among 8 offspring, 5 will be red, 2 black, and 1 white? x 1 = _______ p 1 = _______ x 2 = _______ p 2 = _______ x 3 = _______ p 3 = _______ n = _____ f( __, __; ___, __) =_________ = _________________ 27 ETM 620 - 09 U

Hypergeometric distribution Example*: Automobiles arrive in a dealership in lots of 10. Five out of each 10 are inspected. For one lot, it is know that 2 out of 10 do not meet prescribed safety standards. What is probability that at least 1 out of the 5 tested from that lot will be found not meeting safety standards? *from Complete Business Statistics, 4 th ed (Mc. Graw-Hill) 28 ETM 620 - 09 U

This example follows a hypergeometric distribution: A random sample of size n is selected without replacement from N items. k of the N items may be classified as “successes” and N-k are “failures. ” The probability associated with getting x successes in the sample (given k successes in the lot. ) Where, k = number of “successes” = 2 N = the lot size = 10 29 n = number in sample = 5 x = number found = 1 or 2 ETM 620 - 09 U

Hypergeometric distribution In our example, = _______________ 30 ETM 620 - 09 U

Expectations of the hypergeometric The mean and variance of the hypergeometric distribution are given by What are the expected number of cars that fail inspection in our example? What is the standard deviation? μ = ______ σ2 = _____ , σ = _____ 31 ETM 620 - 09 U

Your turn … A worn machine tool produced defective parts for a period of time before the problem was discovered. Normal sampling of each lot of 20 parts involves testing 6 parts and rejecting the lot if 2 or more are defective. If a lot from the worn tool contains 3 defective parts: 1. What is the expected number of defective parts in a sample of six from the lot? 2. What is the expected variance? 3. What is the probability that the lot will be rejected? 32 ETM 620 - 09 U

Binomial approximation Note, if N >> n, then we can approximate this with the binomial distribution. For example: Automobiles arrive in a dealership in lots of 100. 5 out of each 100 are inspected. 2 /10 (p=0. 2) are indeed below safety standards. What is probability that at least 1 out of 5 will be found not meeting safety standards? Recall: P(X ≥ 1) = 1 – P(X < 1) = 1 – P(X = 0) Hypergeometric distribution 33 Binomial distribution ETM 620 - 09 U

Negative binomial (Pascal) distribution Example: Historical data indicates that 30% of all bits transmitted through a digital transmission channel are received in error. An engineer is running an experiment to try to classify these errors, and will start by gathering data on the first 10 errors encountered. What is the probability that the 10 th error will occur on the 25 th trial? 34 ETM 620 - 09 U

This example follows a negative binomial distribution: Repeated independent trials. Probability of success = p and probability of failure = q = 1 -p. Random variable, X, is the number of the trial on which the rth success occurs. Note: when r is an integer value this is referred to as a Pascal distribution. The probability associated with the rth success occurring on trial x is given by, Where, r = “success number” = 10 x = trial number on which r occurs = 25 p = probability of success (error) = 0. 3 q = 1 – p = 0. 7 35 ETM 620 - 09 U

Negative Binomial Distribution In our example, = _______________ ETM 620 - 09 U 36

Poisson process The number of occurrences in a given interval or region with the following properties: “memoryless” P(occurrence) during a very short interval or small region is proportional to the size of the interval and doesn’t depend on number occurring outside the region or interval. P(X>1) in a very short interval is negligible Examples: Number of bits transmitted per minute. Number of calls to customer service in an hour. Number of bacteria in a given sample. Number of hurricanes per year in a given region. 37 ETM 620 - 09 U

Poisson Process Example An average of 2. 7 service calls per minute are received at a particular maintenance center. The calls correspond to a Poisson process. To determine personnel and equipment needs to maintain a desired level of service, the plant manager needs to be able to determine the probabilities associated with numbers of service calls. What is the probability that fewer than 2 calls will be received in any given minute? 38 ETM 620 - 09 U

Poisson Distribution The probability associated with the number of occurrences in a given period of time is given by, Where, λ = average number of outcomes per unit time or region = 2. 7 t = time interval or region = 1 minute 39 ETM 620 - 09 U

Our example The probability that fewer than 2 calls will be received in any given minute is … P(X < 2) = P(X = 0) + P(X = 1) = _____________ The mean and variance are both λt, so μ = ___________ Note: Table I, pp. 598 -600, gives Σt p(x; λt) In Excel, the function =POISSON(x, mean, cumulative) gives the cumulative distribution function (when cumulative = “true” or 1) and the probability mass function (when cumulative = “false” or 0). 40 ETM 620 - 09 U

Poisson distribution If more than 6 calls are received in a 3 -minute period, an extra service technician will be needed to maintain the desired level of service. What is the probability of that happening? μ = λt = ___________ P(X > 6) = 1 – P(X < 6) = ___________ 41 ETM 620 - 09 U

Poisson distribution 42 ETM 620 - 09 U

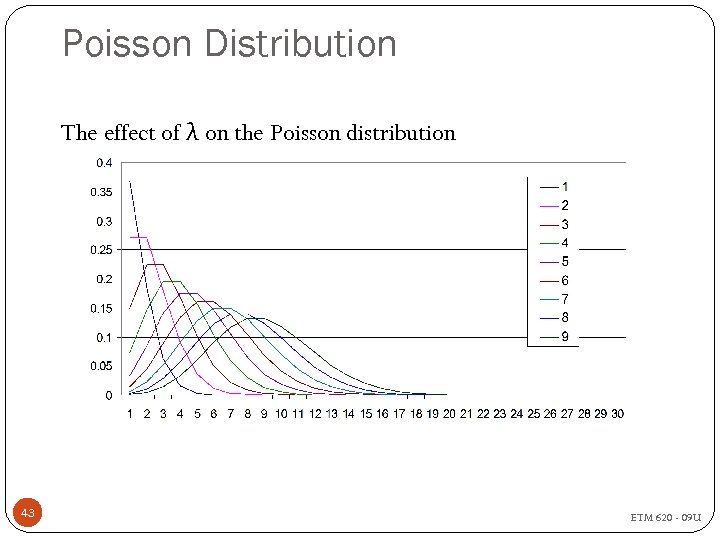
Poisson Distribution The effect of λ on the Poisson distribution 43 ETM 620 - 09 U