9056c1ac6e488a343516add5f7488aa9.ppt
- Количество слайдов: 19
 The Rôle of Price Expectations in the U. K. Housing Market
The Rôle of Price Expectations in the U. K. Housing Market
 Introduction 1. Forward-looking expectations play a crucial ‘lead’ in the determination of house prices for builders, buyers, sellers, etc. 2. The majority of housing studies include only the expectations of the general price level, if they deal with expectations at all. 3. It is suggested in theoretical literature that there is a strong link between housing expectations and the state of the economy. A factor in the latest recession. For example, expectations of falling house prices can reduce consumer spending. 4. The paper explains theoretically the formation of expectations and applies that to RICS survey data of house price expectations over the next three months, or more, in conjunction with both the Nationwide and Halifax actual house price indices. 1
Introduction 1. Forward-looking expectations play a crucial ‘lead’ in the determination of house prices for builders, buyers, sellers, etc. 2. The majority of housing studies include only the expectations of the general price level, if they deal with expectations at all. 3. It is suggested in theoretical literature that there is a strong link between housing expectations and the state of the economy. A factor in the latest recession. For example, expectations of falling house prices can reduce consumer spending. 4. The paper explains theoretically the formation of expectations and applies that to RICS survey data of house price expectations over the next three months, or more, in conjunction with both the Nationwide and Halifax actual house price indices. 1
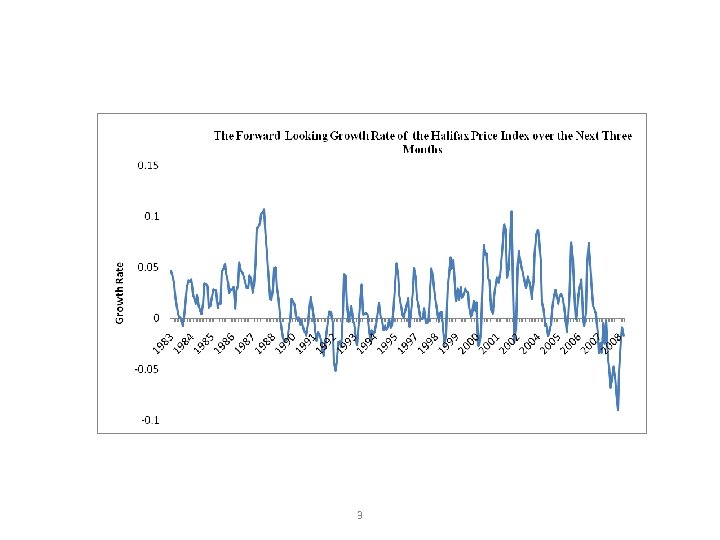
 The Data 1. There are several sources of actual data on house prices: the Halifax, the Nationwide, the Land Registry and the Financial Times indices. 2. The mortgage lenders’ series provide the longest run of monthly, non-seasonal statistics, and therefore, are adopted in this empirical investigation. Also, the Land Registry series is ‘behind the times’ because it lags actual transactions; the lenders’ series by contrast, lead transactions. 3. The Figure on the next slide shows the fluctuations in the logarithmic growth rate of Halifax prices over the next three months, that is the logarithm at time (T+4) minus the logarithm at time (T+1). The Nationwide index would give similar results. 2
The Data 1. There are several sources of actual data on house prices: the Halifax, the Nationwide, the Land Registry and the Financial Times indices. 2. The mortgage lenders’ series provide the longest run of monthly, non-seasonal statistics, and therefore, are adopted in this empirical investigation. Also, the Land Registry series is ‘behind the times’ because it lags actual transactions; the lenders’ series by contrast, lead transactions. 3. The Figure on the next slide shows the fluctuations in the logarithmic growth rate of Halifax prices over the next three months, that is the logarithm at time (T+4) minus the logarithm at time (T+1). The Nationwide index would give similar results. 2
 3
3
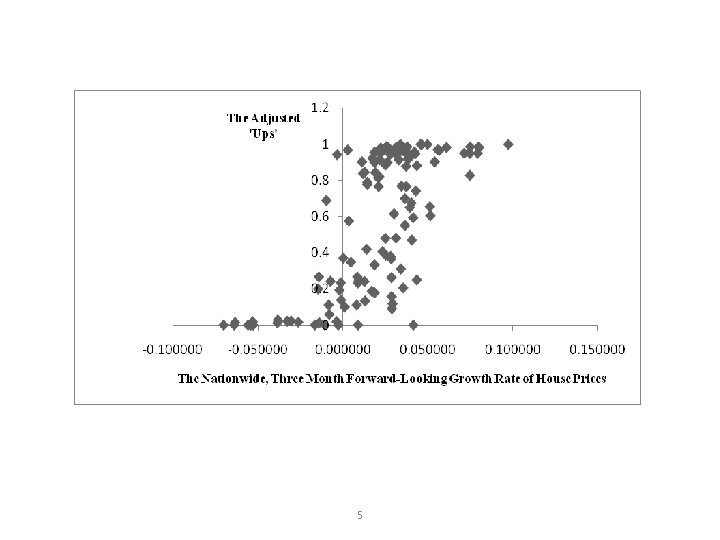
 The Theoretical Model 1. The formation of forward-looking expectations can be modelled on the basis of bounded rationality and the interdependence of agents, described as a process of diffusion. 2. Those agents with the resources to form accurate expectations cheaply are a small number of chartered surveyors who possess the knowledge of the market and are part of an Institution that publishes the expectations in the form of either ‘up’, ‘same’ or ‘down’. 3. This group is small relative to the majority, which means that the distribution of expectations will be initially slow, followed by a sudden increase as the majority of agents adapt to the change in predictions. 4. This sequence implies a non–linear process of diffusion, which can be captured by the logistic function, represented by a S-shaped curve, shown in the next slide. 4
The Theoretical Model 1. The formation of forward-looking expectations can be modelled on the basis of bounded rationality and the interdependence of agents, described as a process of diffusion. 2. Those agents with the resources to form accurate expectations cheaply are a small number of chartered surveyors who possess the knowledge of the market and are part of an Institution that publishes the expectations in the form of either ‘up’, ‘same’ or ‘down’. 3. This group is small relative to the majority, which means that the distribution of expectations will be initially slow, followed by a sudden increase as the majority of agents adapt to the change in predictions. 4. This sequence implies a non–linear process of diffusion, which can be captured by the logistic function, represented by a S-shaped curve, shown in the next slide. 4
 5
5
 The Empirical Estimation of the Diffusion Model 1. A logistic model of expectation diffusion is estimated using the RICS data on future price trends. Given that the ‘sames’ have changed considerably over the time period, it is necessary to normalise the data. 2. The ‘ups’ and ‘downs’ can be normalised so they sum to one (or hundred), by calculating adjusted variables. Then, either one of normalised ‘ups’ or normalised ‘downs’ can be used because they give perfectly symmetric results. 3. A technical difficulty, however, is that the normalised ‘ups’ contain some zeros, and it was not possible to calculate the logarithms for them. To overcome this problem, the zeros were adjusted to 0. 005 and the “ones” reduced to 0. 995 so that the logistic variable could be derived. 6
The Empirical Estimation of the Diffusion Model 1. A logistic model of expectation diffusion is estimated using the RICS data on future price trends. Given that the ‘sames’ have changed considerably over the time period, it is necessary to normalise the data. 2. The ‘ups’ and ‘downs’ can be normalised so they sum to one (or hundred), by calculating adjusted variables. Then, either one of normalised ‘ups’ or normalised ‘downs’ can be used because they give perfectly symmetric results. 3. A technical difficulty, however, is that the normalised ‘ups’ contain some zeros, and it was not possible to calculate the logarithms for them. To overcome this problem, the zeros were adjusted to 0. 005 and the “ones” reduced to 0. 995 so that the logistic variable could be derived. 6
 More on Empirical Estimation 4. The statistical analysis, which explains the logistic diffusion variable derived from the RICS survey using the adjusted ‘ups’, employed the Hendry methodology of general-to-specific analysis together with price data from the Halifax database over the period of 1999 M: 10 to 2009 M: 9. This is followed with the substitute data set, the Nationwide, over the same period. 5. The significant variables in the equations are explained on the next slides. 6. Both empirical models are similar. 7
More on Empirical Estimation 4. The statistical analysis, which explains the logistic diffusion variable derived from the RICS survey using the adjusted ‘ups’, employed the Hendry methodology of general-to-specific analysis together with price data from the Halifax database over the period of 1999 M: 10 to 2009 M: 9. This is followed with the substitute data set, the Nationwide, over the same period. 5. The significant variables in the equations are explained on the next slides. 6. Both empirical models are similar. 7
 Halifax Model explaining RICS • The dependent variable is the change in the log(au/(1 -au)) from the RICS survey; • Explained by the forward-looking growth in the Halifax price index, logarithm T+4 minus logarithm T+1; • The dependent variable lagged 1, 5, 9 and 15 months; • The Halifax growth lagged 16, 21 and 22 months; • One dummy variable for September in 2004; • The dynamics here are quite complicated, suggesting some form of error correction. 8
Halifax Model explaining RICS • The dependent variable is the change in the log(au/(1 -au)) from the RICS survey; • Explained by the forward-looking growth in the Halifax price index, logarithm T+4 minus logarithm T+1; • The dependent variable lagged 1, 5, 9 and 15 months; • The Halifax growth lagged 16, 21 and 22 months; • One dummy variable for September in 2004; • The dynamics here are quite complicated, suggesting some form of error correction. 8
 Nationwide Model explaining RICS • The dependent variable is the change in log(au/(1 -au)) from the RICS survey; • Explained by the forward-looking growth in the Nationwide price index, logarithm T+4 minus logarithm T+1, lagged one month; • The dependent variable lagged 5 and 12 months; • The Nationwide growth lagged 14 and 24 months; • Two dummy variables for September 2004 and December 2008. 9
Nationwide Model explaining RICS • The dependent variable is the change in log(au/(1 -au)) from the RICS survey; • Explained by the forward-looking growth in the Nationwide price index, logarithm T+4 minus logarithm T+1, lagged one month; • The dependent variable lagged 5 and 12 months; • The Nationwide growth lagged 14 and 24 months; • Two dummy variables for September 2004 and December 2008. 9
 Econometric Estimation of the Forecasting Models 1. The forecasting of future growth in house prices is causally quite different to the explanation of expectations. Simple reversal of a regression equation in these circumstances is not possible. 2. Given the earlier models, the dependent variable investigated was the change in the logarithms of the house price index data over the next three months, explained by relevant previous price changes and logistic survey variables over the period of 2000 M: 10 to 2009 M: 10. 3. The list of variables with the Halifax series is followed by the alternative observations, the Nationwide, on the next two slides. 4. When comparing the two models, the Nationwide one seems slightly superior statistically, explaining ninety-four per cent of the variation. 10
Econometric Estimation of the Forecasting Models 1. The forecasting of future growth in house prices is causally quite different to the explanation of expectations. Simple reversal of a regression equation in these circumstances is not possible. 2. Given the earlier models, the dependent variable investigated was the change in the logarithms of the house price index data over the next three months, explained by relevant previous price changes and logistic survey variables over the period of 2000 M: 10 to 2009 M: 10. 3. The list of variables with the Halifax series is followed by the alternative observations, the Nationwide, on the next two slides. 4. When comparing the two models, the Nationwide one seems slightly superior statistically, explaining ninety-four per cent of the variation. 10
 Halifax Forecasting Model • The dependent variable is the three months forward-looking growth rate using the Halifax price index; • Explained by the RICS survey diffusion variable, log(au/(1 -au)) and the lagged values of it at 11, 13, 22, and 24 months; • The forward-looking growth rate lagged 1, 3, 4, 6, 7, 9, 10, 12 and 13 months. 11
Halifax Forecasting Model • The dependent variable is the three months forward-looking growth rate using the Halifax price index; • Explained by the RICS survey diffusion variable, log(au/(1 -au)) and the lagged values of it at 11, 13, 22, and 24 months; • The forward-looking growth rate lagged 1, 3, 4, 6, 7, 9, 10, 12 and 13 months. 11
 Nationwide Forecasting Model • The dependent variable is the three months forward-looking growth rate using the Nationwide price index; • Explained by the RICS survey diffusion variable log(au/(1 -au)) lagged 10, 14, 20, 21, 22, 23 and 24 months; • The dependent variable lagged 1, 3, 4, 6, 7, 9, 11, 12, 17, 22 and 24 months. 12
Nationwide Forecasting Model • The dependent variable is the three months forward-looking growth rate using the Nationwide price index; • Explained by the RICS survey diffusion variable log(au/(1 -au)) lagged 10, 14, 20, 21, 22, 23 and 24 months; • The dependent variable lagged 1, 3, 4, 6, 7, 9, 11, 12, 17, 22 and 24 months. 12
 Comparison with an Alternative Form • The logistic forecasting model of the Nationwide was compared with the Pesaran/Thomas (PT) procedure for generating price expectations. The PT procedure involves analysis using the backward-looking survey adjusted ‘ups’ with the inclusion of lagged residuals to explain backward-looking price growth. The coefficients from that analysis are then used in conjunction with forward-looking adjusted ‘ups’ and residuals to generate the expected forward-looking change in house prices. • The root mean squared forecast error (RMSFE) was used to compare three months models. The equation with the logistic function led to lower RMSFE. Results of these tests for the Nationwide model are shown in the paper. • Given the complexity of the dependent variable that developed from Hendry methodology with further restrictions imposed on the model compared with the previous slide, it was decided to experiment with a lag length beyond 3 months. When the lag length was put to 12 months ahead, the equation next was derived. 13
Comparison with an Alternative Form • The logistic forecasting model of the Nationwide was compared with the Pesaran/Thomas (PT) procedure for generating price expectations. The PT procedure involves analysis using the backward-looking survey adjusted ‘ups’ with the inclusion of lagged residuals to explain backward-looking price growth. The coefficients from that analysis are then used in conjunction with forward-looking adjusted ‘ups’ and residuals to generate the expected forward-looking change in house prices. • The root mean squared forecast error (RMSFE) was used to compare three months models. The equation with the logistic function led to lower RMSFE. Results of these tests for the Nationwide model are shown in the paper. • Given the complexity of the dependent variable that developed from Hendry methodology with further restrictions imposed on the model compared with the previous slide, it was decided to experiment with a lag length beyond 3 months. When the lag length was put to 12 months ahead, the equation next was derived. 13
 The Nationwide Forecasting model: Twelve Months Ahead • The dependent variable is the log change of forward-looking growth rate using the Nationwide price index over the next twelve months; • Explained by the RICS survey diffusion variable log(au/(1 -au)) lagged 1, 2, 6, 12, 13, 15 and 23; • The dependent variable lagged 1, 6, 10, 11, 12, 22 and 23 months; • One dummy variable for December 2007; • The statistical model suggests that the Survey data contains more than just three months of information, and could well contain a yearly sequence of events. The answering practices of the surveyors require investigation. 14
The Nationwide Forecasting model: Twelve Months Ahead • The dependent variable is the log change of forward-looking growth rate using the Nationwide price index over the next twelve months; • Explained by the RICS survey diffusion variable log(au/(1 -au)) lagged 1, 2, 6, 12, 13, 15 and 23; • The dependent variable lagged 1, 6, 10, 11, 12, 22 and 23 months; • One dummy variable for December 2007; • The statistical model suggests that the Survey data contains more than just three months of information, and could well contain a yearly sequence of events. The answering practices of the surveyors require investigation. 14
 Forecasts based on the Yearly Model of the Nationwide Price Index • • The study updated the dataset to May 2010, when the Nationwide index was 337. 4603; The previous equation was revised; • The analysis made a forecast for June, then updated the data, and forecast for July, and revised the data again. This process continued until the forecast for December; • • The forecasts are as follows: June - 334. 2268, July – 332. 6814, August – 326. 6403, September – 327. 0887, October – 309. 9837, November – 297. 3425, December – 292. 5050. • The model is forecasting a general decline in the price index with the June value representing a turning-point in the data set. 15
Forecasts based on the Yearly Model of the Nationwide Price Index • • The study updated the dataset to May 2010, when the Nationwide index was 337. 4603; The previous equation was revised; • The analysis made a forecast for June, then updated the data, and forecast for July, and revised the data again. This process continued until the forecast for December; • • The forecasts are as follows: June - 334. 2268, July – 332. 6814, August – 326. 6403, September – 327. 0887, October – 309. 9837, November – 297. 3425, December – 292. 5050. • The model is forecasting a general decline in the price index with the June value representing a turning-point in the data set. 15
 The Policy Implications of The Work 1. The work shows precisely how the RICS survey can be used to forecast the Halifax and Nationwide house price indices. 2. Expectations of future house prices are important for buyers (will prices go up after purchase? ), sellers (could more be derived by selling later? ), builders (will the house started fetch a profit on completion? ) and should be important for the Government and the Bank of England (for example, what will the effect on consumer spending be? ). 3. Expectations influence mortgage lenders. If expectations are for falling prices, they are reluctant to lend and tend to ration credit because of the greater probability of default. If expectations are for rising prices, lenders tend to make loans to a greater range of borrowers because of the rising value of collateral. 16
The Policy Implications of The Work 1. The work shows precisely how the RICS survey can be used to forecast the Halifax and Nationwide house price indices. 2. Expectations of future house prices are important for buyers (will prices go up after purchase? ), sellers (could more be derived by selling later? ), builders (will the house started fetch a profit on completion? ) and should be important for the Government and the Bank of England (for example, what will the effect on consumer spending be? ). 3. Expectations influence mortgage lenders. If expectations are for falling prices, they are reluctant to lend and tend to ration credit because of the greater probability of default. If expectations are for rising prices, lenders tend to make loans to a greater range of borrowers because of the rising value of collateral. 16
 Government’s Housing Policy 1. It would be useful to supplement this study with a co-integration VAR analysis incorporating the RICS survey data, to investigate the housing market ‘fundamentals’ which affect house price expectations most, in both the short and long runs. 2. This would be a useful study because the Government can only realistically affect market expectations indirectly, through market ‘fundamentals’. 3. The first target of policy historically has tended to be housing finance; interest rates and mortgage lender regulation. 4. The second target historically has tended to be housing supply, using local authorities and planning approval. 17
Government’s Housing Policy 1. It would be useful to supplement this study with a co-integration VAR analysis incorporating the RICS survey data, to investigate the housing market ‘fundamentals’ which affect house price expectations most, in both the short and long runs. 2. This would be a useful study because the Government can only realistically affect market expectations indirectly, through market ‘fundamentals’. 3. The first target of policy historically has tended to be housing finance; interest rates and mortgage lender regulation. 4. The second target historically has tended to be housing supply, using local authorities and planning approval. 17
 Conclusions/Summary • The study has focused on the process of the formation of expectations of house prices underlying the RICS Survey; • The empirical investigation suggests that there is a diffusion process, captured by the logistic model. This is in line with models of bounded rationality, where decision-making is uncertain, self-fulfilling, complex and costly; • The majority of agents in the market follow the few, the alphas of the pack, namely the Chartered Surveyors. 18
Conclusions/Summary • The study has focused on the process of the formation of expectations of house prices underlying the RICS Survey; • The empirical investigation suggests that there is a diffusion process, captured by the logistic model. This is in line with models of bounded rationality, where decision-making is uncertain, self-fulfilling, complex and costly; • The majority of agents in the market follow the few, the alphas of the pack, namely the Chartered Surveyors. 18
