14022015лаб.pptx
- Количество слайдов: 44

The problem – условие задачи Task solution- решение задачи Believe – считать Therefore – следовательно Reciprocating-возвратно-поступательный there are two cases – возможны два случая the answer to the problem - ответ задачи

• Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия. • Основная задача динамики - для данного тела по известной силе найти его ускорение и, наоборот, по известному ускорению найти результирующую силу, действующую на тело.

• Масса m - физическая величина, характеризующая количество вещества, инертность, гравитационные свойства и энергию материального тела. Массу тела, определяющую его инертные свойства, называют инертной массой. • Импульс p (количество движения) - физическая величина, опи-сывающая свойства движущихся тел, равная произведению массы на скорость.

II закон Ньютона -основной в динамике, при описании движения тел под действием приложенных к ним сил II закон Ньютона имеет другую формулировку И через импульс

связь изменения импульса тела и времени действия силы: это импульс силы. Сила тяжести. Эта сила направлена вертикально вниз, ее модуль:

На любое тело массы m вблизи поверхности Земли действует гравитационная сила Сила трения скольжения: сила нормального давления, прижимающая друг к другу трущиеся поверхности тел. Сила трения, всегда направлена противоположно вектору скорости тела, на которое она действует.

Сила упругости: величина упругой деформации тела. Минус в правой части выражения означает, что сила упругости направлена противоположно деформации. the force of elasticity

Сила трения лодки массой m о воду прямо пропорциональна квадрату ее скорости (коэффициент пропорциональности k). Лодка двигалась со скоростью v 0. Найти время, в течение которого скорость лодки уменьшится в два раза.

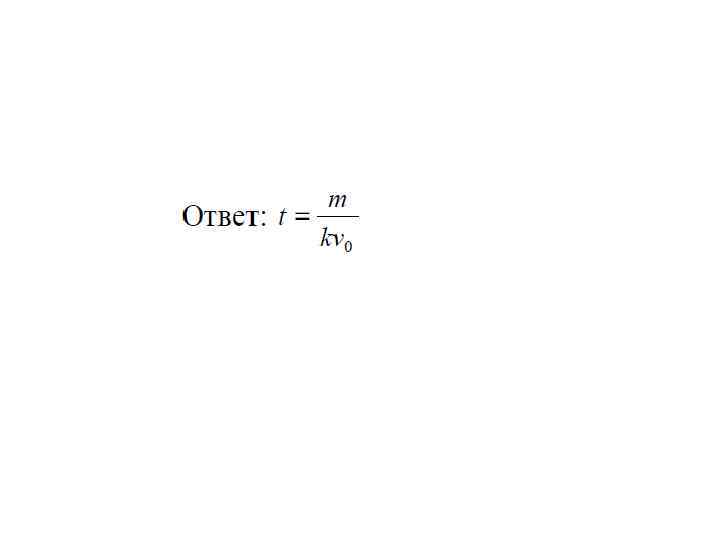

• Энергия - количественная величина и качественная характеристика движения и взаимодействия материи ( matter) во всех ее превращениях. Энергия есть функция состояния ( status) системы и характеризует способности системы совершить работу. • Изменение энергии при переходе системы из одного состояния в другое равно работе, совершаемой системой в процессе перехода:

• Диссипация (рассеяние) энергии механических систем - процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления). • Диссипативные системы - системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.

• Механическая энергия - физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи. • Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения.

Кинетическая энергия системы - сумма кинетических энергий отдельных тел (материальных точек) этой системы: Связь между кинетической энергией тела (системы) и его импульсом:

• Потенциальная энергия - физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в систе-ме. • Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком: d. W= -d. A

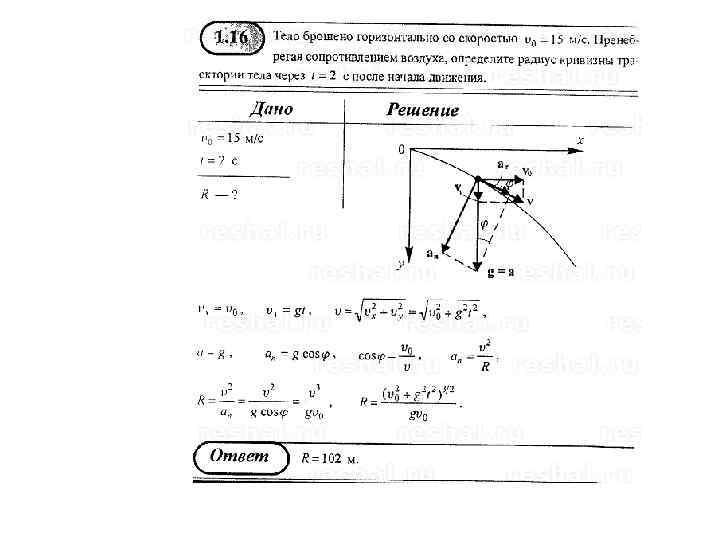
Движение материальной точки задано радиус -вектором: Определить промежуток времени Δt, по истечении которого точка вернется в исходную позицию и путь s, который она при этом пройдет.

• Задачки из группы в VK. COM • Раздел документы • Файл «задачник ч-в. djvu»


• Колебания, это процессы, точно или приблизительно повторяющиеся во времени. • - изменение координаты шарика, подвешенного на нити и отклоненного от вертикали; • - изменение силы тока в электрической цепи;

• Осциллятор – физическая система, совершающая колебания. Система, у которой величины, описывающие ее, периодически меняются с течением времени. • Гармонический осциллятор – механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины которой изменяются по гармоническому закону (закону синуса или косинуса).

Физическое тело или совокупность тел, которые при выведении их из состояния устойчивого равновесия совершают колебания, называются колебательной системой. При колебаниях значения физических величин, характеризующих колебательную систему, повторяются через определенные промежутки времени.

Наименьший промежуток времени, через который колебательная система возвращается в первоначальное состояние, называется периодом колебаний Т. За период Т система совершает одно полное колебание.

Колебания характеризуются также частотой ν и циклической частотой ω. Частотой колебаний ν называется величина обратная периоду и численно равная числу полных колебаний, совершаемых системой в единицу времени

• Циклической или круговой частотой ω называется величина равная

Если изменения во времени колеблющейся величины происходят по закону синуса или косинуса, то такие колебания называются гармоническими. Они описываются уравнением типа:

Величина x называется смещением. Смещение – это координата колеблющейся точки, которую отсчитывают от положения равновесия. • oscillation, vibration • displacement, shift, redshift

Фаза колебаний – это аргумент, функцией которого является состояние колебательной системы в каждый момент времени. Фаза измеряется в угловых единицах – радианах (долях π).

• Значение фазы в момент 0=t называется начальной фазой колебаний. Выбор начального момента совершенно произволен. Можно выбрать этот момент так, что начальная фаза будет равна нулю. • ТОГДА:
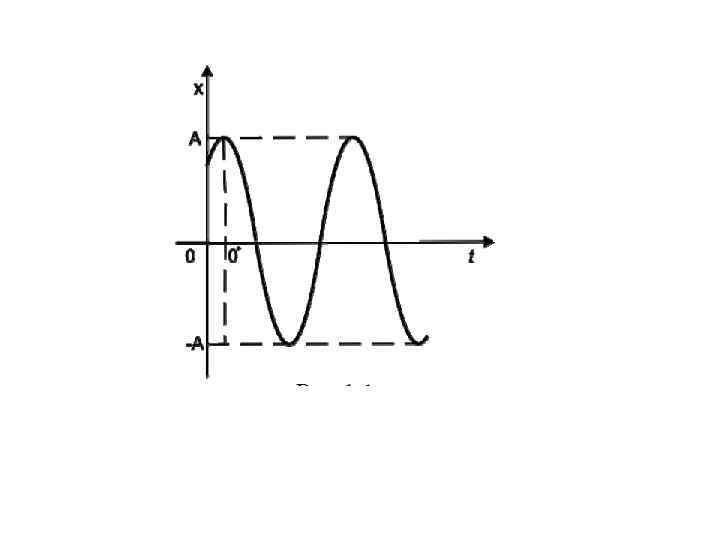

Поскольку функция косинус изменяется в пределах от -1 до +1, то смещение х может принимать значения. Максимальная величина смещения называется амплитудой Ax=max. скорость колеблющейся точки

Погрешности измерений погрешность измерения – measurement accuracy погрешность измерений – measurement uncertainty • • Погрешность является неотъемлемой частью любого измерения. Погрешность – количественная характеристика неопределенности, или неоднозначности, результата измерения. Ее оценивают, исходя из всей информации, накопленной при подготовке и выполнении измерений. Эту информацию обрабатывают для совместного одновременного определения окончательного результата измерения и его погрешности. Окончательный результат нельзя расценивать как “истинное значение” измеряемой физической величины, так как в этом нет смысла из-за наличия погрешности. Погрешность может быть выражена в единицах измеряемой величины x, – в таком случае она обозначается Dx и носит название абсолютной погрешности. Однако абсолютная погрешность зачастую не отражает качества измерений. Действительно, абсолютная погрешность 1 метр при измерении расстояния от Земли до Луны свидетельствует о высоком качестве измерения, та же погрешность совершенно неприемлема при измерении роста человека. Критерием качества измерения является отношение абсолютной погрешности к окончательному результату измерения Это отношение безразмерно, а dx называют относительной погрешностью и используют как в абсолютном, так и в процентном выражении. Высокой точности измерения соответствует малое значение относительной погрешности. Наоборот, существенная относительная погрешность характеризует малую точность. Рассмотрим основные типы погрешностей, проявляющихся в лабораторных физических экспериментах.

• Промахи или грубые погрешности. • Такие погрешности возникают вследствие неисправности измерительных приборов или ошибок в эксперименте, сделанных по невнимательности. Естественно стремление избегать промахи, но если стало понятно, что они все-таки допущены, соответствующие им результаты измерений просто отбрасывают. Представим следующую ситуацию: с помощью цифрового измерительного прибора проводят исследования электрического тока в цепи. Один из разрядов индикатора используемого прибора неисправен и постоянно воспроизводит ноль. Если этот разряд приходится на первую или вторую цифру результата измерения, то промах неизбежен. • • В процессе непосредственного проведения измерений бывает сложно определить, содержит ли полученный результат промах. Количественный критерий, позволяющий отсеивать такие результаты, рассмотрен ниже.

• • Систематические погрешности. Приборная погрешность. Систематическая погрешность, присутствующая в результатах измерений, выполненных с помощью любого измерительного прибора, как правило, неизвестна и не может быть учтена. Ее можно оценить только путем сравнения показаний прибора с показаниями другого, более точного. Иногда результаты специально проведенного сравнения приводят в паспорте прибора, однако чаще указывают максимально возможную погрешность для приборов данного типа. Модельная погрешность. В основу любого экспериментального исследования, сопряженного с измерениями, заложена модель. Модель содержит наиболее полное физическое описание исследуемого объекта или процесса, которое позволяет составить его математическое описание, а именно, набор математических соотношений, включающих в себя физические величины. Они выступают в роли переменных и параметров, которыми могут быть величины, непосредственно измеряемые в ходе эксперимента, и величины, значения которых требуется определить, исходя из всей совокупности экспериментальных данных. В итоге модель представляет собой математическую конструкцию, базирующуюся на физических представлениях. Только на основании эксперимента можно сделать обоснованное заключение о приемлемости описания полученных данных с помощью использованной теоретической модели. Зафиксированные несоответствия построенной модели, фактически – теории, и эксперимента, служат важнейшим стимулом развития науки, требуя уточнять представления о природе окружающего физического мира. В свое время именно отчетливо зарегистрированные несоответствия привели к созданию теории равновесного теплового излучения, квантовой механики, теории относительности. С другой стороны, неверно построенная модель, в которой не нашли отражения какие-то важные процессы или факторы, влияющие на результат измерений, также приводит к несоответствиям. Как следствие, измеряемые в эксперименте величины, вычисляемые по полученным из модели рабочим формулам, содержат погрешности, которые носят название модельных погрешностей. В эксперименте лабораторную установку стараются поместить в такие условия, которые были бы максимально близки к требованиям модели. Однако полностью исключить несоответствие модели и экспериментальной ситуации удается далеко не всегда.

• • • В качестве модельной погрешности, например, можно рассматривать неучтенное изменение напряжения на исследуемом с применением вольтметра участке электрической цепи. Оно возникает из-за шунтирования цепи внутренним сопротивлением вольтметра. Отклонение результатов измерений можно компенсировать введением поправок к показаниям вольтметра, но существеннее другое – при наличии в цепи вольтметра, как следствие, изменяются электрические процессы в ней. Значит, первоначальная модель процессов в этой цепи, не рассматривающая включение вольтметра, может оказаться неточной. К разряду модельных может быть отнесена погрешность взвешивания на рычажных весах. Согласно закону Архимеда вес тела и гирь уменьшается изза действия выталкивающей силы воздуха. Напомним, что 1 куб. м. воздуха весит примерно 10 Н. Для того, чтобы правильно найти массу взвешиваемого тела, опять же, нужно ввести поправки на потерю веса гирями и самим телом. Вместе с тем, как и при любых измерениях, здесь необходим разумный подход. Например, при работе с грубыми техническими весами бессмысленно вводить поправку на Архимедову силу, так как она окажется много меньше погрешностей, вносимых в результат измерения гирями и самими весами. Следует особо отметить, что модельные погрешности являются наиболее сложными для анализа и учета.

• Случайные погрешности. • Из самого названия следует, что при повторных измерениях погрешности этого типа демонстрируют свою случайную природу. Возникают они вследствие множества причин, совместное воздействие которых на каждое отдельное измерение невозможно учесть или заранее установить. Такими причинами могут оказаться, к примеру, незначительные колебания температуры различных деталей и узлов установки, скачки напряжения, вибрации, турбулентные движения воздуха, трение в механизмах, ошибки считывания показаний приборов и т. п. Единственно возможный способ объективного учета случайных погрешностей состоит в определении их статистических закономерностей, проявляющихся в результатах многократных измерений. Рассчитанные статистические оценки вносят в окончательный результат измерения. • случайная погрешность -random error

• Контрольные вопросы 1. Что такое погрешность измерения ? 2. Чем абсолютная погрешность отличается от относительной ? 3. Чем характеризуют качество измерения ? 4. Каковы причины появления промахов ? 5. Что такое систематическая погрешность ? 6. Какова роль модельных несоответствий в развитии науки ? 7. Что такое случайная погрешность и какие причины приводят к ее появлению ?

• • • Основным типом погрешностей, изучению которых посвящено последующее изложение, являются случайные погрешности. Они поддаются строгому математическому описанию, что позволяет делать выводы о качестве измерений, в которых они присутствуют. Погрешности других типов более сложны для анализа, их выявляют и анализируют только в условиях конкретного эксперимента. Чтобы знать, как надлежит работать со случайными погрешностями, прежде всего рассмотрим приемы статистического описания случайных величин. • Получение распределения случайной величины и его описание Рассмотрение начнем с предполагаемого эксперимента, в котором выполняют многократные прямые измерения какой-то случайной физической величины, проводимые без изменения условий эксперимента. Закономерности в поведении величины видны из гистограммы. Гистограмма – ступенчатая диаграмма, показывающая как часто при измерениях появляются результаты, попадающие в тот или иной интервал Dx между наименьшим xmin и наибольшим xmax из измеренных значений величины x. Гистограмму строят в следующих координатах: по оси абсцисс откладывают измеряемую величину x, по оси ординат – Dn/n. Dx (рис. 3. 1). Здесь n – полное количество проведенных измерений, Dn – количество результатов, попавших в интервал [x, x+Dx]. •

• • • Отношение Dn/n есть доля результатов, оказавшихся в указанном интервале. Оно имеет смысл вероятности попадания результата отдельного измерения в данный интервал. Выражение Dn/(n. Dx), получаемое после деления Dn/n на ширину интервала Dx, приобретает смысл плотности вероятности. При очень большом количестве измерений (n) весь диапазон изменения величины x можно разбить на бесконечно малые интервалы dx , как это делается в математике, и найти количество результатов dn в каждом из них. В этом случае гистограмма превратится в плавную кривую – график функции Такую функцию называют плотностью вероятности, или распределением вероятности, иногда – просто распределением величины x. • Распределение выступает в роли исчерпывающей характеристики случайной величины. Закон распределения можно задать в виде функционального выражения, графика, таблицы или каким-то другим способом. При любом варианте задания устанавливается связь между вероятностью того, что результат однократного измерения случайной величины попадет в заданный интервал возможных значений, и шириной этого интервала. • Распределение содержит наиболее полную информацию о случайной величине, однако пользоваться им не всегда удобно. Оперируя результатами проведенного эксперимента, вместо функции распределения лучше иметь привычные числовые величины – ими являются среднее значение и дисперсия. • Среднее значение измеряемой величины x указывает центр распределения, около которого группируются результаты отдельных измерений

Дисперсию (variance) вводят как средний квадрат отклонения (deviation) отдельных результатов от среднего значения случайной величины Среднее квадратичное отклонение , называемое также стандартным, определяют как квадратный корень из дисперсии случайная величина - random variable

эта величина характеризует разброс результатов отдельных измерений вокруг среднего значения, получаемого после обработки всех данных многократного измерения. Нормальное распределение Если, помимо характерных для распределения значений величин и s, известен функциональный вид распределения случайной величины, то можно получить полную информацию о вероятности реализации случайной величины в любом заданном интервале значений. Рассмотрим это на примере нормального распределения (normal distribution), или распределения Гаусса. Оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия целого ряда причин, каждая из которых дает малый вклад в погрешность. Причем совершенно неважно, по какому закону распределен каждый из вкладов в отдельности.

• • • Нормально распределенная случайная величина имеет следующие свойства: 1. Она может принимать непрерывный ряд значений от – ? до + ? . 2. Центр распределения случайной величины одновременно является центром симметрии, т. е. одинаковые отклонения результатов измерения в меньшую и в большую стороны от центра встречаются одинаково часто. 3. Малые отклонения встречаются чаще больших, другими словами, реализуются с большей вероятностью. Соответствующее функциональное выражение для распределения задает формула Гаусса выражение exp(y) = e y – экспонента, в которой e = 2, 71828 – основание натуральных логарифмов.
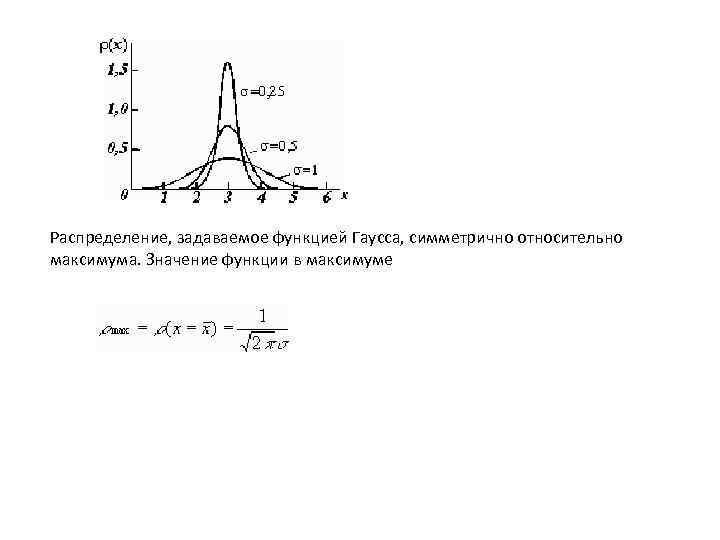
Распределение, задаваемое функцией Гаусса, симметрично относительно максимума. Значение функции в максимуме

• Контрольные вопросы 1. Что такое гистограмма случайной величины и как ее строят ? 2. При каких условиях гистограмма переходит в распределение плотности вероятности ? 3. Что характеризуют средним значением и средним квадратичным отклонением ? Как эти величины оценивают исходя из экспериментальных результатов ? 4. Почему нормальное распределение чаще других встречается вэксперименте ? 5. Какова математическая форма записи нормального распределения с помощью функции Гаусса ?
14022015лаб.pptx