a0e4c9b3c7612fbb471cd78e24a9ccb2.ppt
- Количество слайдов: 157
 The Principle of Direct Syntactic Encoding: All grammatical relation changes are lexical
The Principle of Direct Syntactic Encoding: All grammatical relation changes are lexical
 Two kinds of movement in transformational grammar:
Two kinds of movement in transformational grammar:
 Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]]
Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]]
 Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren
Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren
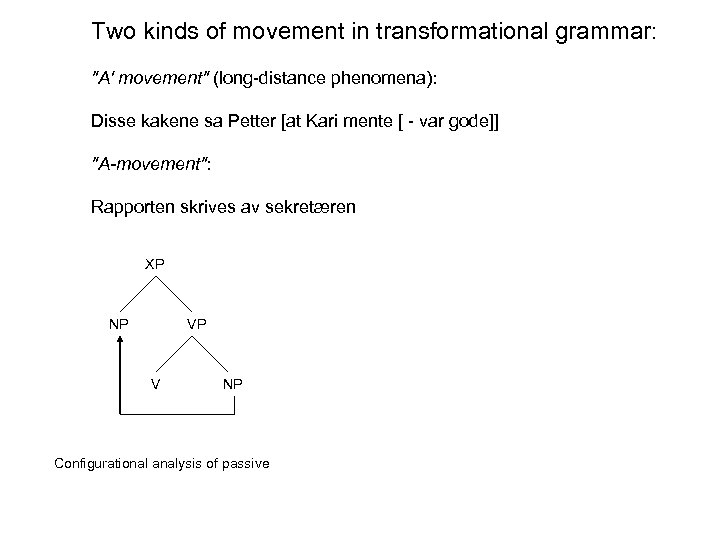 Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren XP NP VP V NP Configurational analysis of passive
Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren XP NP VP V NP Configurational analysis of passive
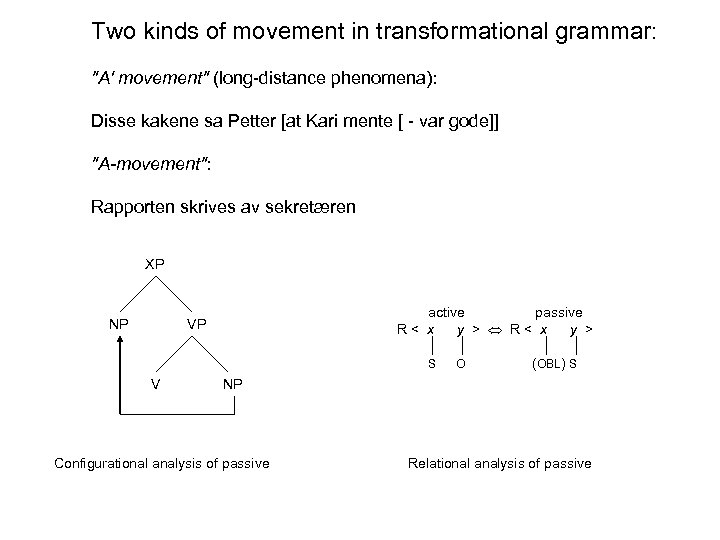 Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren XP NP active passive R< x y > R < x y > VP S V O (OBL) S NP Configurational analysis of passive Relational analysis of passive
Two kinds of movement in transformational grammar: "A' movement" (long-distance phenomena): Disse kakene sa Petter [at Kari mente [ - var gode]] "A-movement": Rapporten skrives av sekretæren XP NP active passive R< x y > R < x y > VP S V O (OBL) S NP Configurational analysis of passive Relational analysis of passive
 The seeming movement under passivization in English is simply a consequence of the configurational assignment of GFs in that language: XP VP V ( SUBJ) NP ( CF) NP CF = non-discourse argument functions
The seeming movement under passivization in English is simply a consequence of the configurational assignment of GFs in that language: XP VP V ( SUBJ) NP ( CF) NP CF = non-discourse argument functions
 In a non-configurational language like Malayalam there is no seeming movement under passivization:
In a non-configurational language like Malayalam there is no seeming movement under passivization:
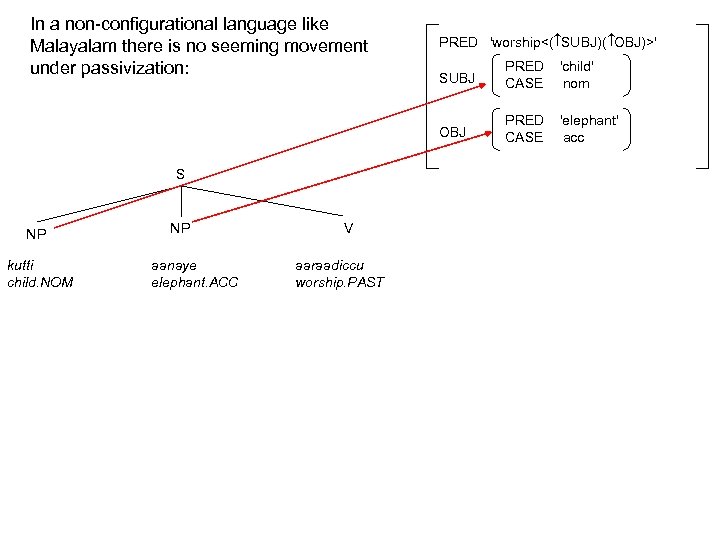 In a non-configurational language like Malayalam there is no seeming movement under passivization: PRED 'worship<( SUBJ)( OBJ)>' NP kutti child. NOM NP aanaye elephant. ACC V aaraadiccu worship. PAST PRED CASE 'child' nom OBJ S SUBJ PRED CASE 'elephant' acc
In a non-configurational language like Malayalam there is no seeming movement under passivization: PRED 'worship<( SUBJ)( OBJ)>' NP kutti child. NOM NP aanaye elephant. ACC V aaraadiccu worship. PAST PRED CASE 'child' nom OBJ S SUBJ PRED CASE 'elephant' acc
 In a non-configurational language like Malayalam there is no seeming movement under passivization: PRED 'worship<( SUBJ)( OBJ)>' SUBJ PRED CASE 'child' nom OBJ PRED CASE 'elephant' acc S kutti child. NOM NP aanaye elephant. ACC V aaraadiccu worship. PAST NP PRED 'worship<( OBLag)( SUBJ)>' OBLag NP kuttiyaal child. INSTR NP aana elephant. NOM V aaraadhikkappettu worship. PASS. PAST 'child' instr SUBJ S PRED CASE 'elephant' nom
In a non-configurational language like Malayalam there is no seeming movement under passivization: PRED 'worship<( SUBJ)( OBJ)>' SUBJ PRED CASE 'child' nom OBJ PRED CASE 'elephant' acc S kutti child. NOM NP aanaye elephant. ACC V aaraadiccu worship. PAST NP PRED 'worship<( OBLag)( SUBJ)>' OBLag NP kuttiyaal child. INSTR NP aana elephant. NOM V aaraadhikkappettu worship. PASS. PAST 'child' instr SUBJ S PRED CASE 'elephant' nom
 The classical LFG passive analysis: A lexical redundancy rule A pattern in the lexicon writes written write < SUBJ OBJ > write < OBLag/ SUBJ > eats eaten eat < SUBJ OBJ > eat < OBLag/ SUBJ > buys bought buy < SUBJ OBJ > buy < OBLag/ SUBJ > . . .
The classical LFG passive analysis: A lexical redundancy rule A pattern in the lexicon writes written write < SUBJ OBJ > write < OBLag/ SUBJ > eats eaten eat < SUBJ OBJ > eat < OBLag/ SUBJ > buys bought buy < SUBJ OBJ > buy < OBLag/ SUBJ > . . .
 The classical LFG passive analysis: A lexical redundancy rule A pattern in the lexicon writes written write < SUBJ OBJ > write < OBLag/ SUBJ > eats eaten eat < SUBJ OBJ > eat < OBLag/ SUBJ > buys bought buy < SUBJ OBJ > buy < OBLag/ SUBJ > . . . Abstracted as a lexical rule: OBJ ⇒ SUBJ ⇒ OBLag SUBJ ⇒
The classical LFG passive analysis: A lexical redundancy rule A pattern in the lexicon writes written write < SUBJ OBJ > write < OBLag/ SUBJ > eats eaten eat < SUBJ OBJ > eat < OBLag/ SUBJ > buys bought buy < SUBJ OBJ > buy < OBLag/ SUBJ > . . . Abstracted as a lexical rule: OBJ ⇒ SUBJ ⇒ OBLag SUBJ ⇒
 Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }.
Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }.
 Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }. Template invocation in a lexical entry P: P V @(PASS [(↑PRED)='P<(↑SUBJ)(↑OBJ)>'. . . ])
Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }. Template invocation in a lexical entry P: P V @(PASS [(↑PRED)='P<(↑SUBJ)(↑OBJ)>'. . . ])
 Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }. Template invocation in a lexical entry P: P V @(PASS [(↑PRED)='P<(↑SUBJ)(↑OBJ)>'. . . ]) http: //iness. uib. no/xle-web
Part of the passive template in a Norwegian computational LFG grammar: PASS (SCHEMATA) = { SCHEMATA ~(↑PASSIVE)=+ | SCHEMATA (↑PASSIVE)=c + { (↑OBJ) --> (↑SUBJ) | (↑OBL-TH) --> (↑SUBJ) | (↑OBJ-BEN) --> (↑SUBJ) | (↑COMP) --> (↑SUBJ) | (↑XCOMP) --> (↑SUBJ) } { (↑SUBJ) --> (↑OBL-AG) | (↑SUBJ) --> NULL } }. Template invocation in a lexical entry P: P V @(PASS [(↑PRED)='P<(↑SUBJ)(↑OBJ)>'. . . ]) http: //iness. uib. no/xle-web
 Grammatical Functions TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
Grammatical Functions TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
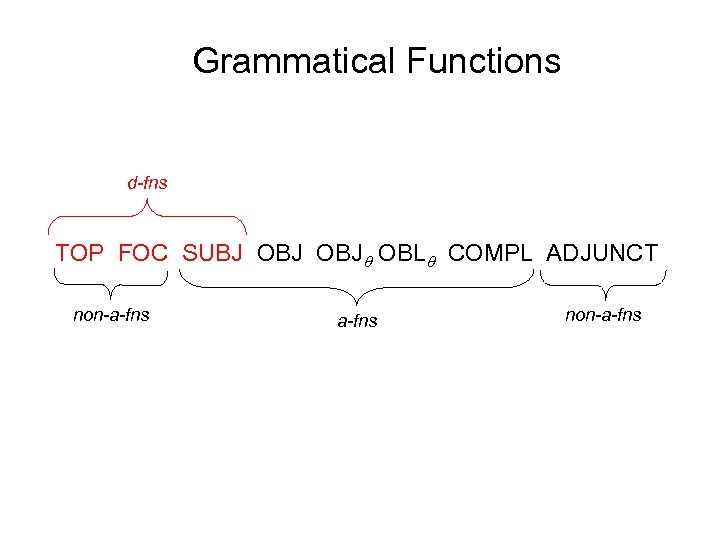 Grammatical Functions d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
Grammatical Functions d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
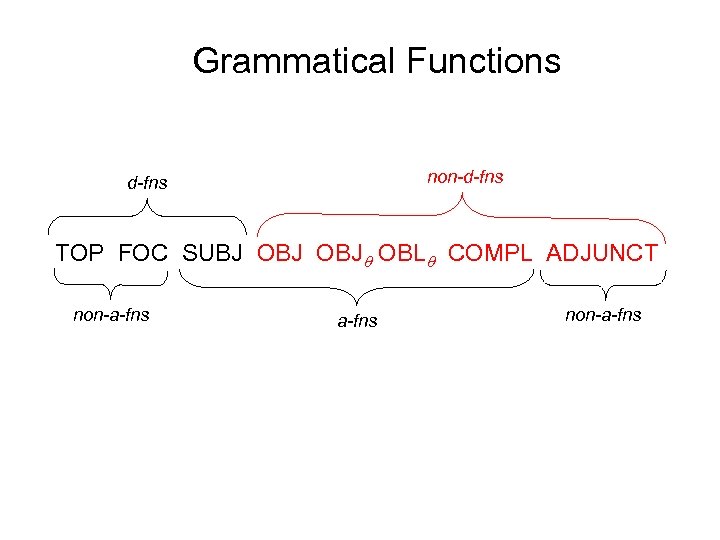 Grammatical Functions non-d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
Grammatical Functions non-d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
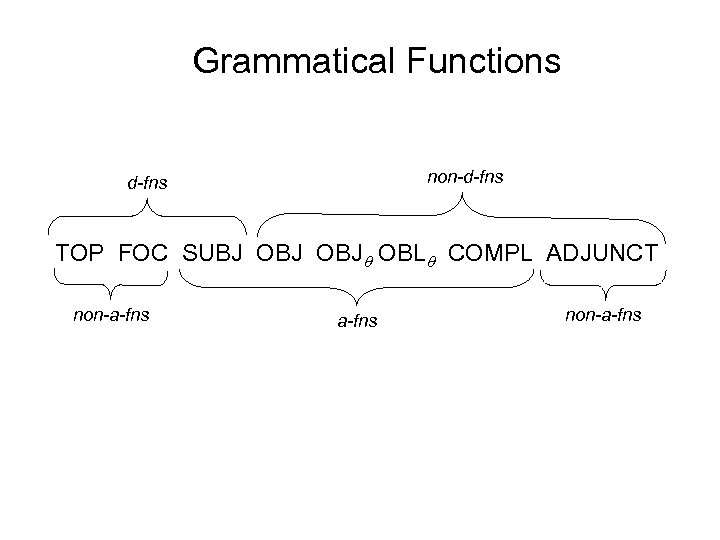 Grammatical Functions non-d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
Grammatical Functions non-d-fns TOP FOC SUBJ OBJ OBL COMPL ADJUNCT non-a-fns
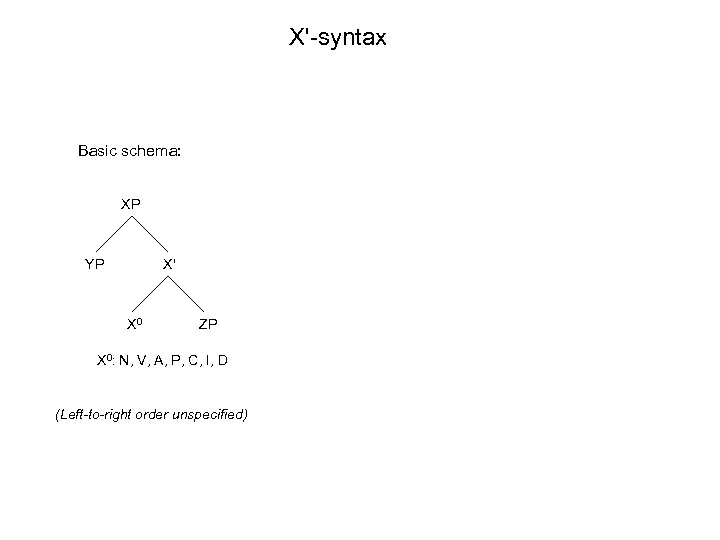 X'-syntax Basic schema: XP YP X' X 0 ZP X 0: N, V, A, P, C, I, D (Left-to-right order unspecified)
X'-syntax Basic schema: XP YP X' X 0 ZP X 0: N, V, A, P, C, I, D (Left-to-right order unspecified)
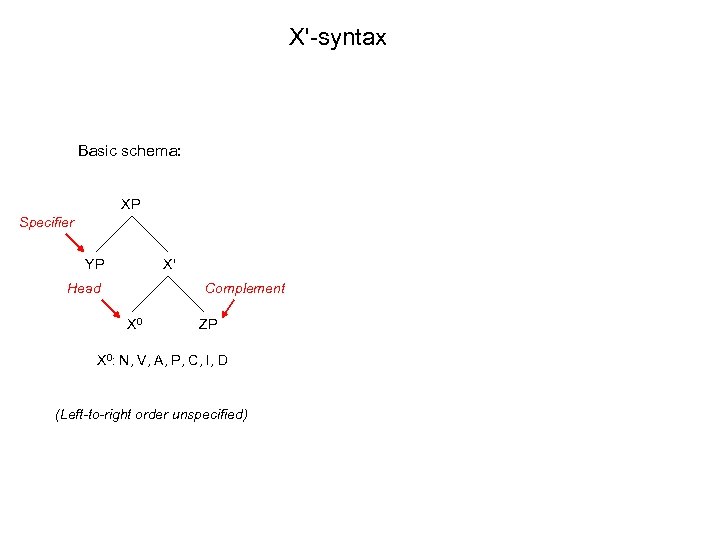 X'-syntax Basic schema: XP Specifier YP X' Head Complement X 0 ZP X 0: N, V, A, P, C, I, D (Left-to-right order unspecified)
X'-syntax Basic schema: XP Specifier YP X' Head Complement X 0 ZP X 0: N, V, A, P, C, I, D (Left-to-right order unspecified)
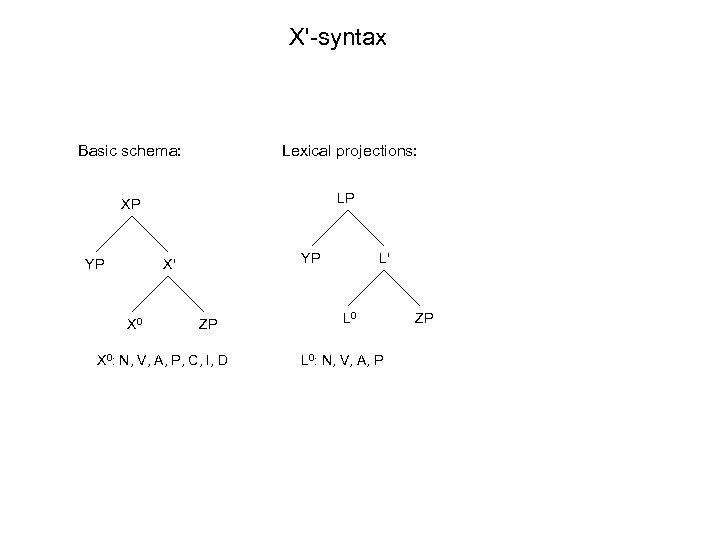 X'-syntax Basic schema: Lexical projections: XP LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P ZP
X'-syntax Basic schema: Lexical projections: XP LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P ZP
 X'-syntax Basic schema: Lexical projections: XP NP YP YP X' N' Cæsar's X 0 ZP X 0: N, V, A, P, C, I, D N 0 conquest L 0: N, V, A, P ZP of Gallia
X'-syntax Basic schema: Lexical projections: XP NP YP YP X' N' Cæsar's X 0 ZP X 0: N, V, A, P, C, I, D N 0 conquest L 0: N, V, A, P ZP of Gallia
 X'-syntax Basic schema: Lexical projections: XP VP YP YP X' V' Cæsar X 0 ZP X 0: N, V, A, P, C, I, D V 0 ZP conquered Gallia L 0: N, V, A, P
X'-syntax Basic schema: Lexical projections: XP VP YP YP X' V' Cæsar X 0 ZP X 0: N, V, A, P, C, I, D V 0 ZP conquered Gallia L 0: N, V, A, P
 X'-syntax Basic schema: Lexical projections: XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D V 0 ZP conquered Gallia L 0: N, V, A, P
X'-syntax Basic schema: Lexical projections: XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D V 0 ZP conquered Gallia L 0: N, V, A, P
 X'-syntax Basic schema: Lexical projections: XP YP AP X' X 0 ZP X 0: N, V, A, P, C, I, D A 0 afraid L 0: N, V, A, P ZP of dogs
X'-syntax Basic schema: Lexical projections: XP YP AP X' X 0 ZP X 0: N, V, A, P, C, I, D A 0 afraid L 0: N, V, A, P ZP of dogs
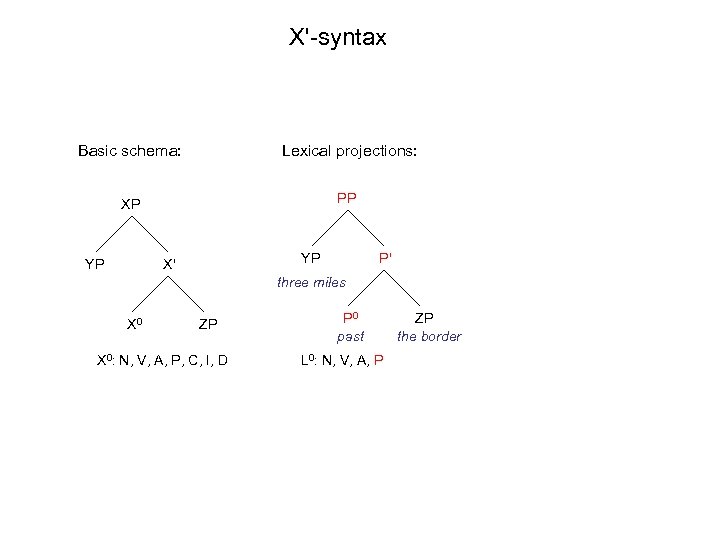 X'-syntax Basic schema: Lexical projections: XP PP YP YP X' P' three miles X 0 ZP X 0: N, V, A, P, C, I, D P 0 past L 0: N, V, A, P ZP the border
X'-syntax Basic schema: Lexical projections: XP PP YP YP X' P' three miles X 0 ZP X 0: N, V, A, P, C, I, D P 0 past L 0: N, V, A, P ZP the border
 X'-syntax Basic schema: Lexical projections: XP YP PP X' X 0 ZP X 0: N, V, A, P, C, I, D P 0 on L 0: N, V, A, P ZP the table
X'-syntax Basic schema: Lexical projections: XP YP PP X' X 0 ZP X 0: N, V, A, P, C, I, D P 0 on L 0: N, V, A, P ZP the table
 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D ZP
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D ZP
 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P CP ZP C 0 that F 0: C, I, D ZP Mary left
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P CP ZP C 0 that F 0: C, I, D ZP Mary left
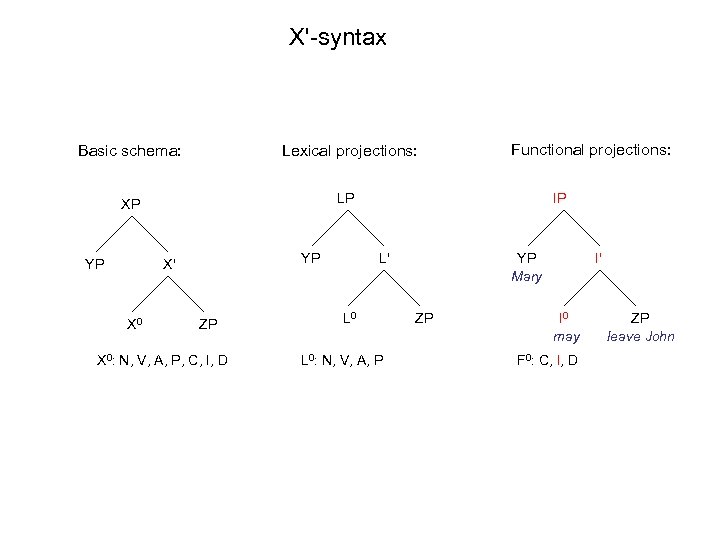 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D IP L' L 0: N, V, A, P YP Mary ZP I' I 0 may F 0: C, I, D ZP leave John
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D IP L' L 0: N, V, A, P YP Mary ZP I' I 0 may F 0: C, I, D ZP leave John
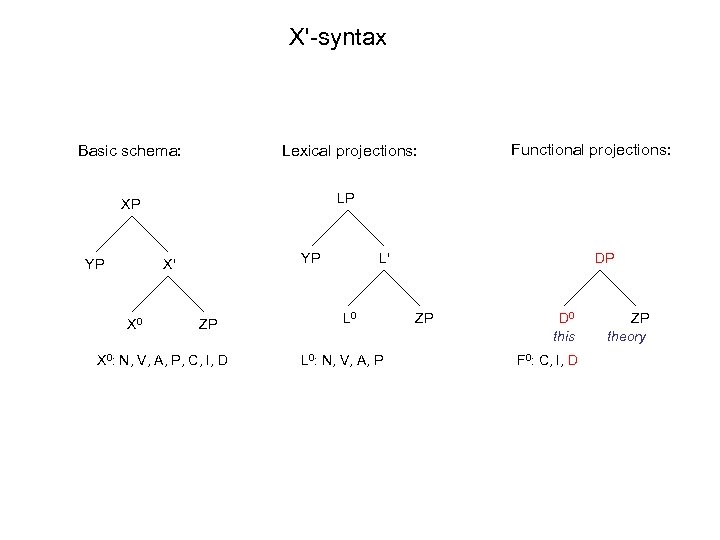 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P DP ZP D 0 this F 0: C, I, D ZP theory
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D L' L 0: N, V, A, P DP ZP D 0 this F 0: C, I, D ZP theory
 X'-syntax Adjunction: XP WP Lexical projections: LP XP YP YP X' X 0 Functional projections: ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D ZP
X'-syntax Adjunction: XP WP Lexical projections: LP XP YP YP X' X 0 Functional projections: ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D ZP
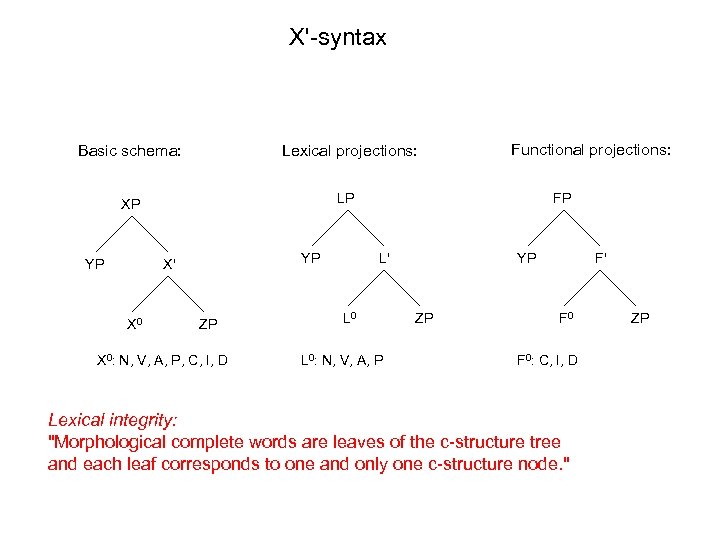 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D Lexical integrity: "Morphological complete words are leaves of the c-structure tree and each leaf corresponds to one and only one c-structure node. " ZP
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D Lexical integrity: "Morphological complete words are leaves of the c-structure tree and each leaf corresponds to one and only one c-structure node. " ZP
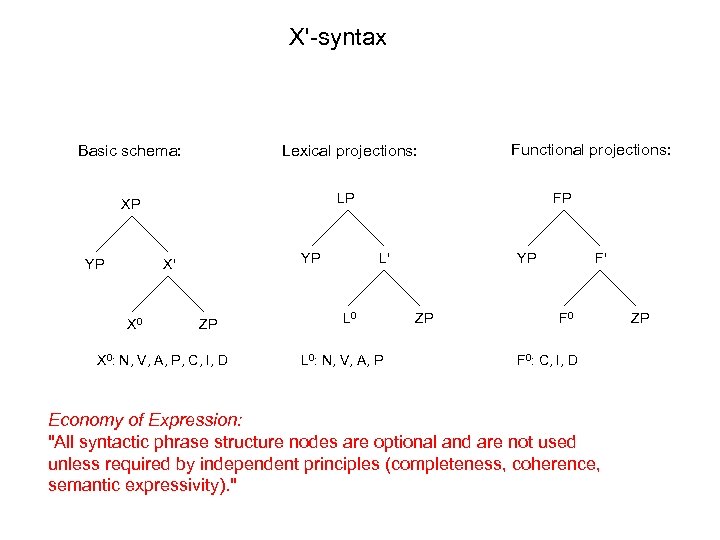 X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
X'-syntax Basic schema: Lexical projections: XP Functional projections: LP YP YP X' X 0 ZP X 0: N, V, A, P, C, I, D FP L' L 0: N, V, A, P YP ZP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
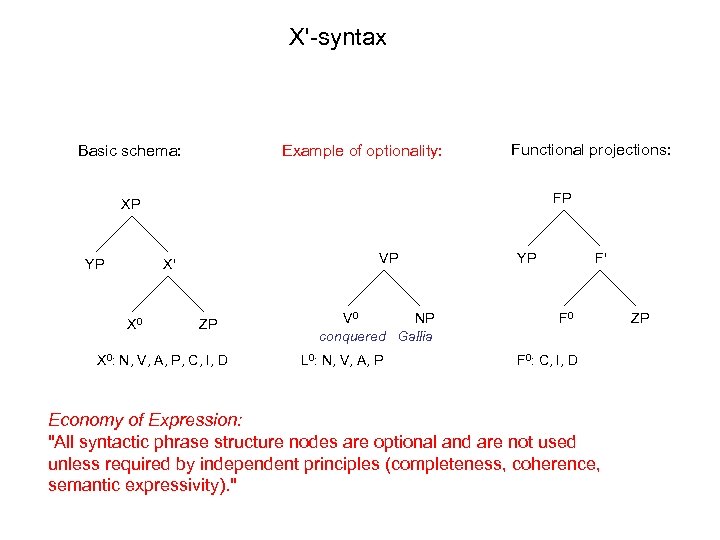 X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D V 0 NP conquered Gallia L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D V 0 NP conquered Gallia L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
 X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 NP Gallia ZP X 0: N, V, A, P, C, I, D L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 NP Gallia ZP X 0: N, V, A, P, C, I, D L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
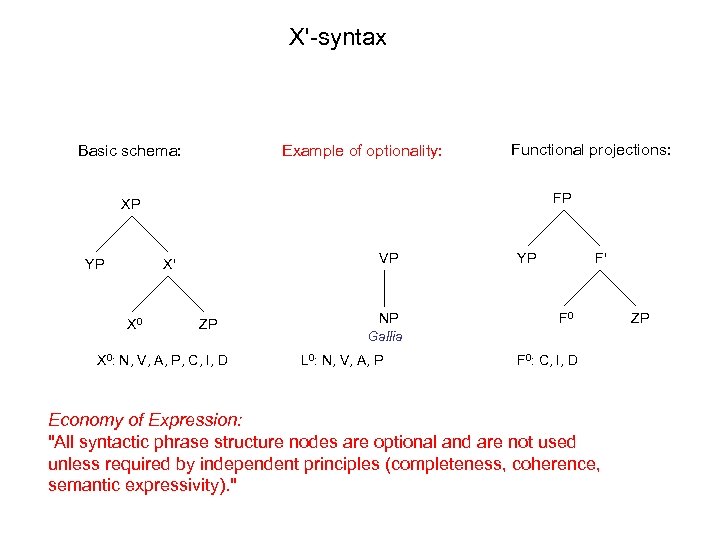 X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D NP Gallia L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
X'-syntax Basic schema: Example of optionality: Functional projections: FP XP YP VP X' X 0 ZP X 0: N, V, A, P, C, I, D NP Gallia L 0: N, V, A, P YP F' F 0: C, I, D Economy of Expression: "All syntactic phrase structure nodes are optional and are not used unless required by independent principles (completeness, coherence, semantic expressivity). " ZP
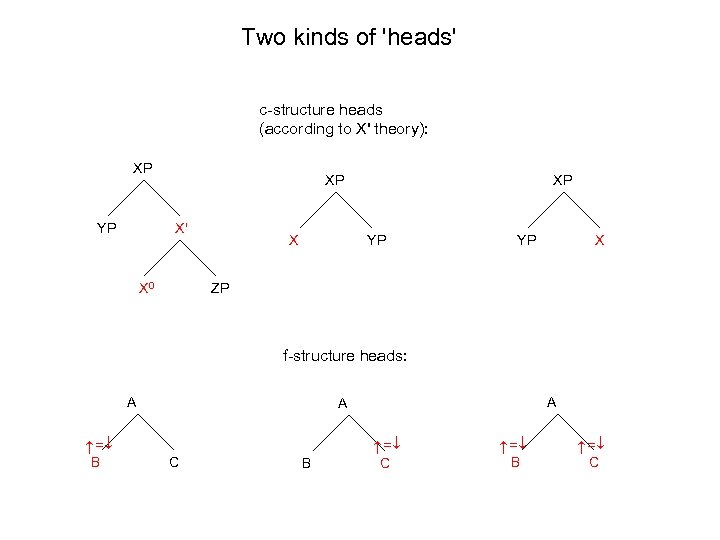 Two kinds of 'heads' c-structure heads (according to X' theory): XP YP XP X' X 0 X XP YP YP X ZP f-structure heads: C C B B A A B A C
Two kinds of 'heads' c-structure heads (according to X' theory): XP YP XP X' X 0 X XP YP YP X ZP f-structure heads: C C B B A A B A C
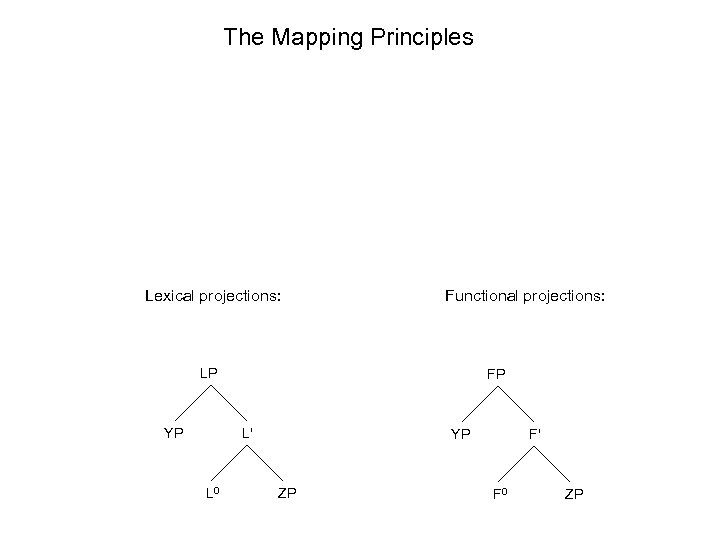 The Mapping Principles Lexical projections: Functional projections: LP YP FP L' L 0 YP ZP F' F 0 ZP
The Mapping Principles Lexical projections: Functional projections: LP YP FP L' L 0 YP ZP F' F 0 ZP
 The Mapping Principles C-structure heads are f-structure heads. Lexical projections: Functional projections: LP FP L 0 L' YP F 0 F' YP a. ZP ZP
The Mapping Principles C-structure heads are f-structure heads. Lexical projections: Functional projections: LP FP L 0 L' YP F 0 F' YP a. ZP ZP
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Lexical projections: Functional projections: LP FP ( DF) YP F 0 F' L 0 L' YP a. b. ZP ZP
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Lexical projections: Functional projections: LP FP ( DF) YP F 0 F' L 0 L' YP a. b. ZP ZP
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Example ([SPEC, IP] as SUBJ): Lexical projections: Functional projections: LP IP L' YP ( SUBJ) NP I' Mary L 0 a. b. ZP I 0 may VP leave John
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Example ([SPEC, IP] as SUBJ): Lexical projections: Functional projections: LP IP L' YP ( SUBJ) NP I' Mary L 0 a. b. ZP I 0 may VP leave John
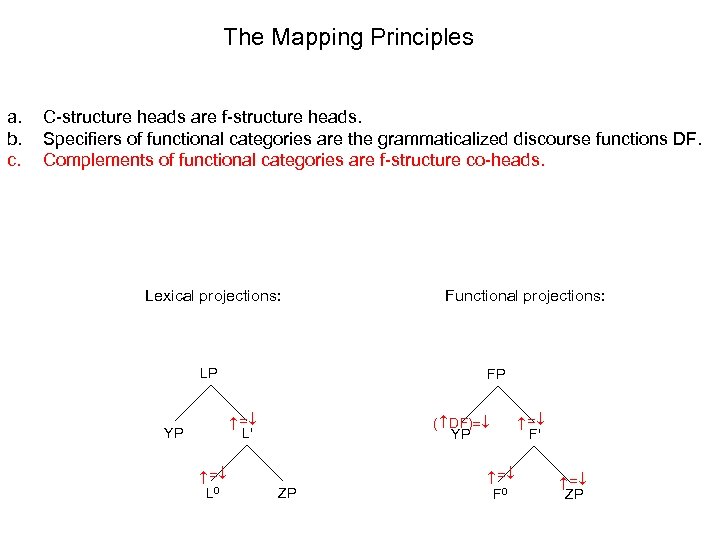 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Lexical projections: Functional projections: LP FP ( DF) YP F 0 ZP F' ZP L 0 L' YP a. b. c.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Lexical projections: Functional projections: LP FP ( DF) YP F 0 ZP F' ZP L 0 L' YP a. b. c.
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Example 1 (VP as co-head with I): Lexical projections: Functional projections: LP IP L' YP ( SUBJ) NP I' Mary L 0 ZP I 0 may VP leave John a. b. c.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Example 1 (VP as co-head with I): Lexical projections: Functional projections: LP IP L' YP ( SUBJ) NP I' Mary L 0 ZP I 0 may VP leave John a. b. c.
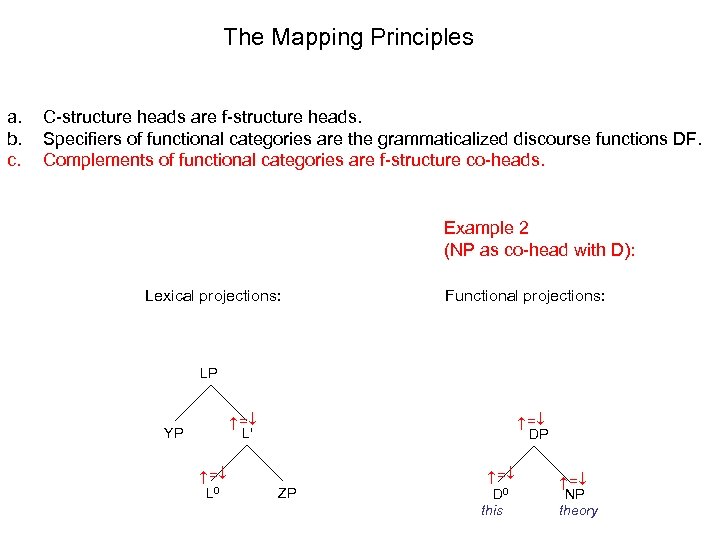 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Example 2 (NP as co-head with D): Lexical projections: Functional projections: LP D 0 this L 0 L' ZP DP NP theory YP a. b. c.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Example 2 (NP as co-head with D): Lexical projections: Functional projections: LP D 0 this L 0 L' ZP DP NP theory YP a. b. c.
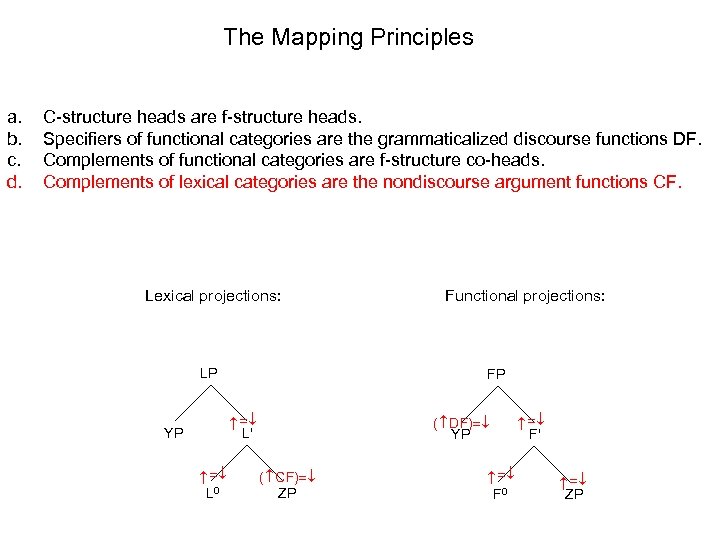 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Lexical projections: Functional projections: LP FP ( DF) YP F 0 ( CF) ZP F' ZP L 0 L' YP a. b. c. d.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Lexical projections: Functional projections: LP FP ( DF) YP F 0 ( CF) ZP F' ZP L 0 L' YP a. b. c. d.
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Example 1 (DP as OBJ of P): Lexical projections: Functional projections: PP ( DF) YP F 0 ( OBJ) DP the border F' ZP P 0 past P' YP three miles FP a. b. c. d.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Example 1 (DP as OBJ of P): Lexical projections: Functional projections: PP ( DF) YP F 0 ( OBJ) DP the border F' ZP P 0 past P' YP three miles FP a. b. c. d.
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Example 2 (CP as COMP of V): Lexical projections: Functional projections: FP F 0 ( COMP) CP that John left F' ZP ( DF) YP VP V 0 said a. b. c. d.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Example 2 (CP as COMP of V): Lexical projections: Functional projections: FP F 0 ( COMP) CP that John left F' ZP ( DF) YP VP V 0 said a. b. c. d.
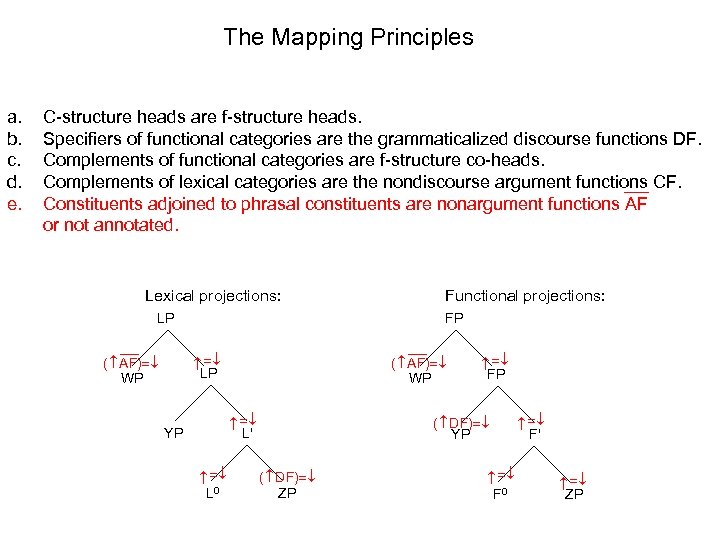 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Lexical projections: Functional projections: FP LP ( AF) WP ( DF) YP ( DF) ZP F 0 L 0 L' YP FP ( AF) WP F' ZP LP a. b. c. d. e.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Lexical projections: Functional projections: FP LP ( AF) WP ( DF) YP ( DF) ZP F 0 L 0 L' YP FP ( AF) WP F' ZP LP a. b. c. d. e.
 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 1 (preposed adjunct): Lexical projections: Functional projections: IP ( SUBJ) NP Mary L 0 L' YP IP ( DF) ZP ( ADJUNCT) AP unfortunately I 0 will I' VP leave John LP ( AF) WP LP a. b. c. d. e.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 1 (preposed adjunct): Lexical projections: Functional projections: IP ( SUBJ) NP Mary L 0 L' YP IP ( DF) ZP ( ADJUNCT) AP unfortunately I 0 will I' VP leave John LP ( AF) WP LP a. b. c. d. e.
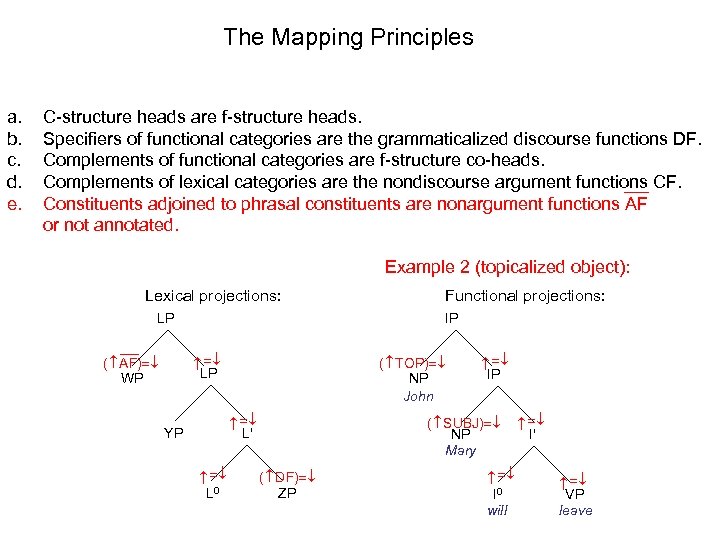 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 2 (topicalized object): Lexical projections: Functional projections: IP ( SUBJ) NP Mary L 0 L' YP IP ( DF) ZP ( TOP) NP John I 0 will I' VP leave LP ( AF) WP LP a. b. c. d. e.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 2 (topicalized object): Lexical projections: Functional projections: IP ( SUBJ) NP Mary L 0 L' YP IP ( DF) ZP ( TOP) NP John I 0 will I' VP leave LP ( AF) WP LP a. b. c. d. e.
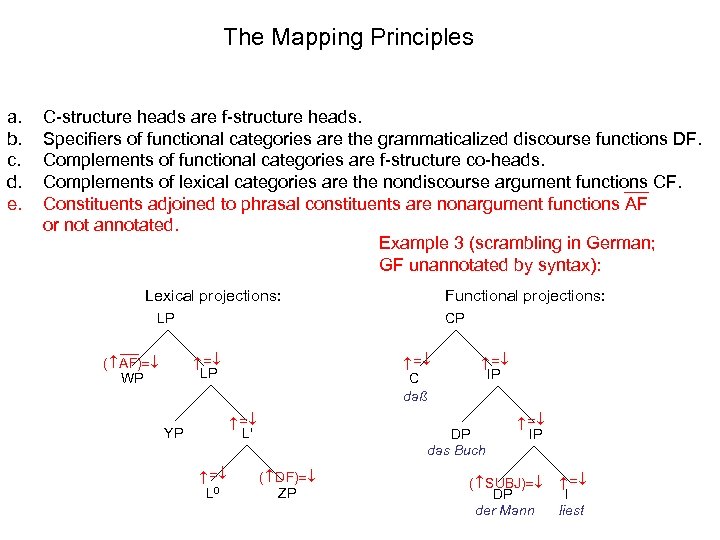 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 3 (scrambling in German; GF unannotated by syntax): Lexical projections: Functional projections: CP C daß DP das Buch L 0 L' ( DF) ZP YP IP ( SUBJ) DP der Mann I liest LP ( AF) WP LP a. b. c. d. e.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 3 (scrambling in German; GF unannotated by syntax): Lexical projections: Functional projections: CP C daß DP das Buch L 0 L' ( DF) ZP YP IP ( SUBJ) DP der Mann I liest LP ( AF) WP LP a. b. c. d. e.
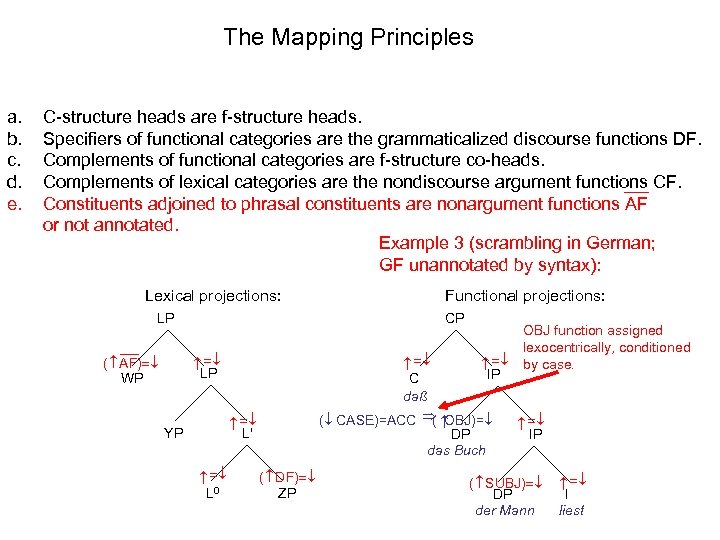 The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 3 (scrambling in German; GF unannotated by syntax): Functional projections: CP LP C daß ( CASE)=ACC ( OBJ)= DP das Buch L' L 0 YP IP ( DF) ZP ( AF) WP OBJ function assigned lexocentrically, conditioned by case. IP ( SUBJ) DP der Mann I liest LP Lexical projections: a. b. c. d. e.
The Mapping Principles C-structure heads are f-structure heads. Specifiers of functional categories are the grammaticalized discourse functions DF. Complements of functional categories are f-structure co-heads. Complements of lexical categories are the nondiscourse argument functions CF. Constituents adjoined to phrasal constituents are nonargument functions AF or not annotated. Example 3 (scrambling in German; GF unannotated by syntax): Functional projections: CP LP C daß ( CASE)=ACC ( OBJ)= DP das Buch L' L 0 YP IP ( DF) ZP ( AF) WP OBJ function assigned lexocentrically, conditioned by case. IP ( SUBJ) DP der Mann I liest LP Lexical projections: a. b. c. d. e.
 Example: Annotations constrained by the mapping principles. IP VP V believe ( COMP) CP I' VP I will V leave ( SUBJ) NP Mary C that ( SUBJ) NP I ( ADJUNCT) AP unfortunately ( OBJ) NP John
Example: Annotations constrained by the mapping principles. IP VP V believe ( COMP) CP I' VP I will V leave ( SUBJ) NP Mary C that ( SUBJ) NP I ( ADJUNCT) AP unfortunately ( OBJ) NP John
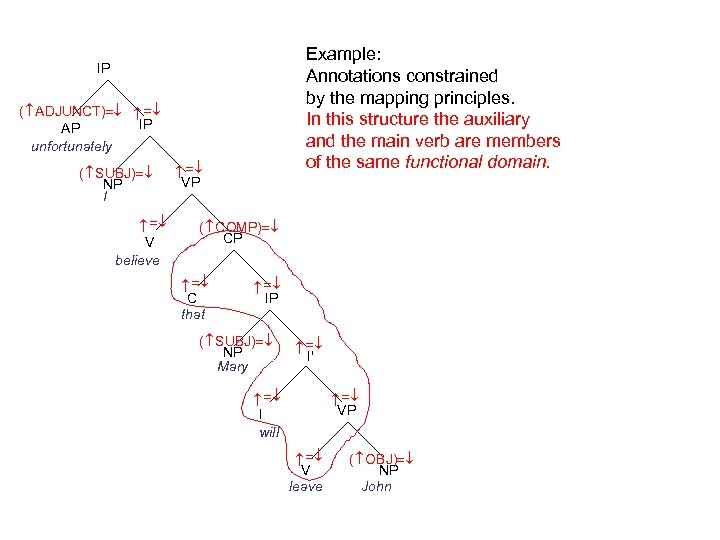 Example: Annotations constrained by the mapping principles. In this structure the auxiliary and the main verb are members of the same functional domain. IP VP V believe ( COMP) CP I' VP I will V leave ( SUBJ) NP Mary C that ( SUBJ) NP I ( ADJUNCT) AP unfortunately ( OBJ) NP John
Example: Annotations constrained by the mapping principles. In this structure the auxiliary and the main verb are members of the same functional domain. IP VP V believe ( COMP) CP I' VP I will V leave ( SUBJ) NP Mary C that ( SUBJ) NP I ( ADJUNCT) AP unfortunately ( OBJ) NP John
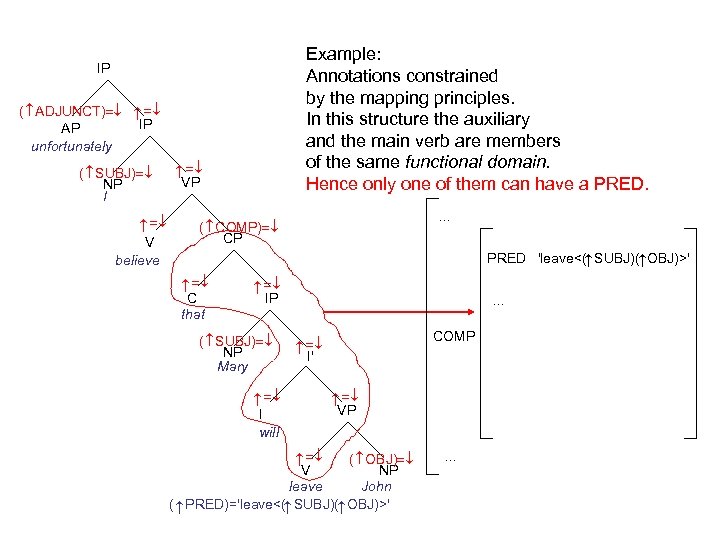 Example: Annotations constrained by the mapping principles. In this structure the auxiliary and the main verb are members of the same functional domain. Hence only one of them can have a PRED. IP VP V believe . . . ( COMP) CP PRED 'leave<( SUBJ)( OBJ)>' C that IP . . . ( SUBJ) NP Mary COMP I' VP I will ( OBJ) V NP leave John ( PRED)='leave<( SUBJ)( OBJ)>' . . . ( SUBJ) NP I ( ADJUNCT) AP unfortunately
Example: Annotations constrained by the mapping principles. In this structure the auxiliary and the main verb are members of the same functional domain. Hence only one of them can have a PRED. IP VP V believe . . . ( COMP) CP PRED 'leave<( SUBJ)( OBJ)>' C that IP . . . ( SUBJ) NP Mary COMP I' VP I will ( OBJ) V NP leave John ( PRED)='leave<( SUBJ)( OBJ)>' . . . ( SUBJ) NP I ( ADJUNCT) AP unfortunately
 In English, auxiliaries are in I, and main verbs always in V IP I' VP I will V leave ( SUBJ) NP Mary ( OBJ) NP John
In English, auxiliaries are in I, and main verbs always in V IP I' VP I will V leave ( SUBJ) NP Mary ( OBJ) NP John
 In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – IP I' VP V leave VP I will ( ADJUNCT) ADV not ( SUBJ) NP Mary ( OBJ) NP John
In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – IP I' VP V leave VP I will ( ADJUNCT) ADV not ( SUBJ) NP Mary ( OBJ) NP John
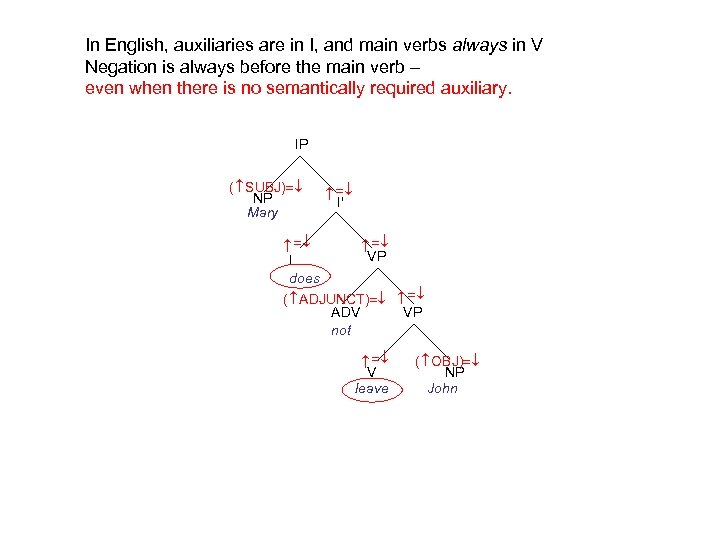 In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – even when there is no semantically required auxiliary. IP I' VP V leave VP I does ( ADJUNCT) ADV not ( SUBJ) NP Mary ( OBJ) NP John
In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – even when there is no semantically required auxiliary. IP I' VP V leave VP I does ( ADJUNCT) ADV not ( SUBJ) NP Mary ( OBJ) NP John
 In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – even when there is no semantically required auxiliary. Hence there is no need to assume that finite main verbs are outside VP. IP V leaves VP ( SUBJ) NP Mary ( OBJ) NP John
In English, auxiliaries are in I, and main verbs always in V Negation is always before the main verb – even when there is no semantically required auxiliary. Hence there is no need to assume that finite main verbs are outside VP. IP V leaves VP ( SUBJ) NP Mary ( OBJ) NP John
 Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I
Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I
 Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I • No specifier of IP, which dominates I and its complement directly.
Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I • No specifier of IP, which dominates I and its complement directly.
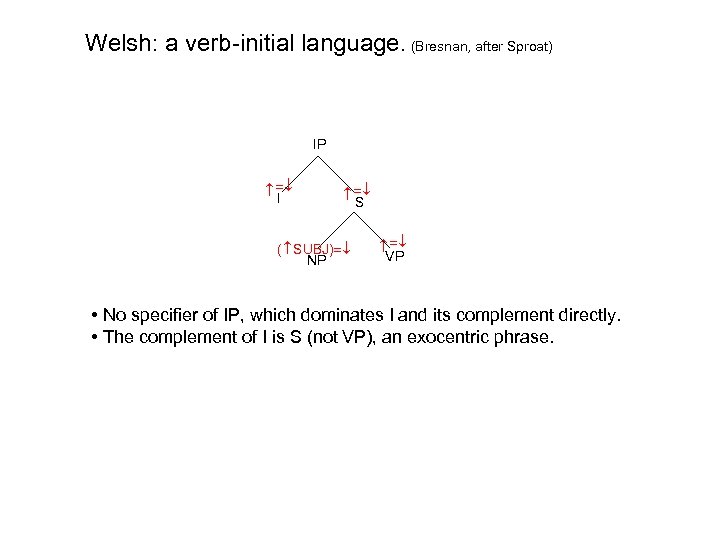 Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I • No specifier of IP, which dominates I and its complement directly. • The complement of I is S (not VP), an exocentric phrase.
Welsh: a verb-initial language. (Bresnan, after Sproat) IP ( SUBJ) NP S VP I • No specifier of IP, which dominates I and its complement directly. • The complement of I is S (not VP), an exocentric phrase.
 Welsh: a verb-initial language. (Bresnan, after Sproat) Auxiliary or main verb may be in I. S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon'
Welsh: a verb-initial language. (Bresnan, after Sproat) Auxiliary or main verb may be in I. S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon'
 Welsh: a verb-initial language. (Bresnan, after Sproat) S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Auxiliary or main verb may be in I. In the latter case, the VP doesn't dominate any V head.
Welsh: a verb-initial language. (Bresnan, after Sproat) S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Auxiliary or main verb may be in I. In the latter case, the VP doesn't dominate any V head.
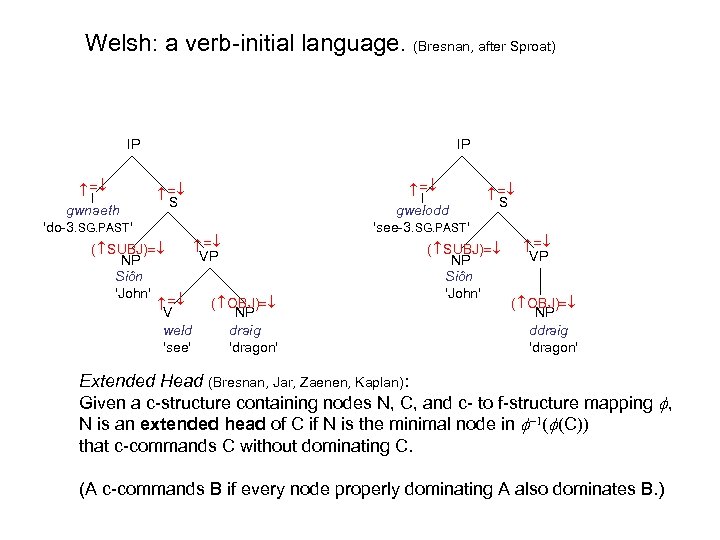 Welsh: a verb-initial language. (Bresnan, after Sproat) S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
Welsh: a verb-initial language. (Bresnan, after Sproat) S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
 Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
 Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
 Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
Welsh: a verb-initial language. (Bresnan, after Sproat) VP S ( SUBJ) NP Siôn 'John' VP ( SUBJ) VP NP Siôn 'John' ( OBJ) V NP weld draig 'see' 'dragon' S I gwelodd 'see-3. SG. PAST' I gwnaeth 'do-3. SG. PAST' IP ( OBJ) NP ddraig 'dragon' Extended Head (Bresnan, Jar, Zaenen, Kaplan): Given a c-structure containing nodes N, C, and c- to f-structure mapping , N is an extended head of C if N is the minimal node in C that c-commands C without dominating C. (A c-commands B if every node properly dominating A also dominates B. )
 Norwegian: a V 2 language.
Norwegian: a V 2 language.
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære • There is a position before the finite verb (unlike Welsh). syntaks
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære • There is a position before the finite verb (unlike Welsh). syntaks
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English).
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English).
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English).
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English).
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English).
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English).
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary.
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary.
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb.
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb.
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb. • Hence the finite verb is always adjacent to its complements: subordinate clauses are not V 2.
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb. • Hence the finite verb is always adjacent to its complements: subordinate clauses are not V 2.
 Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb. • Hence the finite verb is always adjacent to its complements: subordinate clauses are not V 2. Furthermore: • Auxiliaries are fully-fledged, complement taking verbs (unlike English modals).
Norwegian: a V 2 language. Main declarative clauses: Deltagerne ville Heldigvis ville Syntaks ville Deltagerne lærer deltagerne ikke lære syntaks • There is a position before the finite verb (unlike Welsh). • There is only one position before the finite verb: No adjunction of adverbs or topics (unlike English). • There is a subject position after the finite verb (unlike English). • The finite verb – main or auxiliary – is always in the leftmost verbal position, before negation (unlike English). Subordinate clauses: at at deltagerne ikke ville lærer lære syntaks • Negation and other sentence adverbs occur before the finite verb – main or auxiliary. • The subject can only occur before the finite verb. • Hence the finite verb is always adjacent to its complements: subordinate clauses are not V 2. Furthermore: • Auxiliaries are fully-fledged, complement taking verbs (unlike English modals).
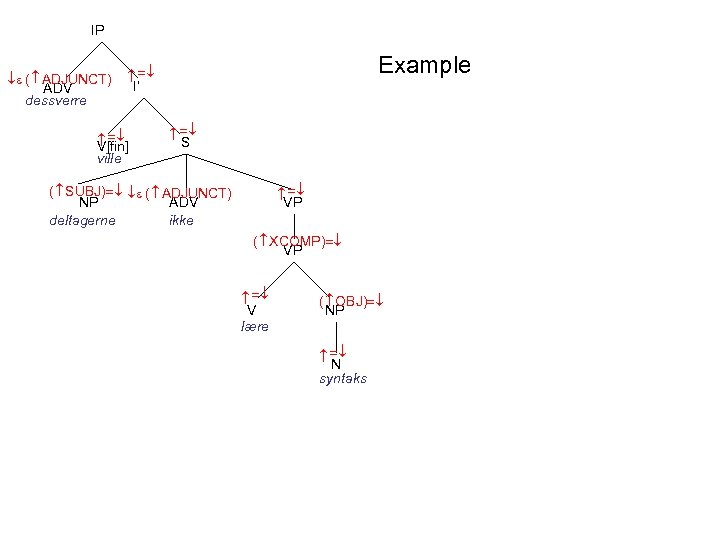 IP Example I’ S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( ADJUNCT) ADV dessverre
IP Example I’ S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( ADJUNCT) ADV dessverre
![IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT)](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-83.jpg) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP
IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP
![IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT)](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-84.jpg) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP
IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP
![IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT)](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-85.jpg) IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP.
IP I’ ( ADJUNCT) ADV dessverre V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP.
![IP SUBJ 1 I’ V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)( IP SUBJ 1 I’ V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)(](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-86.jpg) IP SUBJ 1 I’ V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære PRED ( OBJ) NP N syntaks 'dessverre' PRED 'ikke' ADJUNCT • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP.
IP SUBJ 1 I’ V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære PRED ( OBJ) NP N syntaks 'dessverre' PRED 'ikke' ADJUNCT • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP.
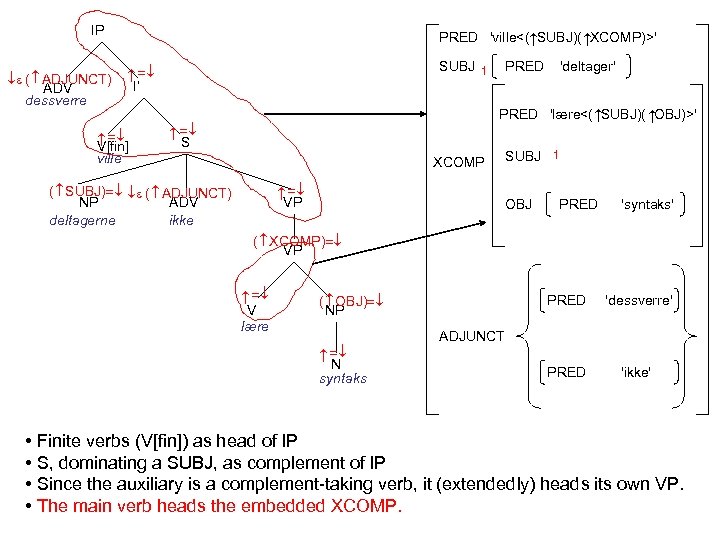 IP SUBJ 1 I’ 'deltager' PRED 'lære<( SUBJ)( OBJ)>' S XCOMP VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)( XCOMP)>' SUBJ 1 OBJ PRED 'syntaks' ( XCOMP) VP V lære PRED ( OBJ) NP N syntaks 'dessverre' PRED 'ikke' ADJUNCT • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP. • The main verb heads the embedded XCOMP.
IP SUBJ 1 I’ 'deltager' PRED 'lære<( SUBJ)( OBJ)>' S XCOMP VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke V[fin] ville PRED ( ADJUNCT) ADV dessverre PRED 'ville<( SUBJ)( XCOMP)>' SUBJ 1 OBJ PRED 'syntaks' ( XCOMP) VP V lære PRED ( OBJ) NP N syntaks 'dessverre' PRED 'ikke' ADJUNCT • Finite verbs (V[fin]) as head of IP • S, dominating a SUBJ, as complement of IP • Since the auxiliary is a complement-taking verb, it (extendedly) heads its own VP. • The main verb heads the embedded XCOMP.
![IP V[fin] ville VP N syntaks ( XCOMP) VP V lære ( OBJ) NP IP V[fin] ville VP N syntaks ( XCOMP) VP V lære ( OBJ) NP](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-88.jpg) IP V[fin] ville VP N syntaks ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
IP V[fin] ville VP N syntaks ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
![IP V[fin] ville VP N syntaks • SPEC of IP can also host the IP V[fin] ville VP N syntaks • SPEC of IP can also host the](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-89.jpg) IP V[fin] ville VP N syntaks • SPEC of IP can also host the subject. ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
IP V[fin] ville VP N syntaks • SPEC of IP can also host the subject. ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
![IP V[fin] ville VP N syntaks • SPEC of IP can also host the IP V[fin] ville VP N syntaks • SPEC of IP can also host the](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-90.jpg) IP V[fin] ville VP N syntaks • SPEC of IP can also host the subject. • Hence two rules in the same functional domain introduce subjects: ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
IP V[fin] ville VP N syntaks • SPEC of IP can also host the subject. • Hence two rules in the same functional domain introduce subjects: ( XCOMP) VP V lære ( OBJ) NP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S ( OBJ) NP N syntaks S I’ V[fin] ville ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP
![IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-91.jpg) IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks subject. IP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville I’ ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP ( OBJ) NP XP ( SUBJ) I' ( ADJUNCT). . . XP ADV* VP' ( SUBJ) ( ADJUNCT) S • SPEC of IP can also host the • Hence two rules in the same functional domain introduce subjects: N syntaks
IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks subject. IP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville I’ ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP ( OBJ) NP XP ( SUBJ) I' ( ADJUNCT). . . XP ADV* VP' ( SUBJ) ( ADJUNCT) S • SPEC of IP can also host the • Hence two rules in the same functional domain introduce subjects: N syntaks
![IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-92.jpg) IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks subject. IP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville I’ ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP ( OBJ) NP XP ( SUBJ) I' ( ADJUNCT). . . XP ADV* VP' ( SUBJ) ( ADJUNCT) S • SPEC of IP can also host the • Hence two rules in the same functional domain introduce subjects: • Functional uniqueness prevents the occurrence of subjects in both positions at once. N syntaks
IP S V[fin] ville VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks subject. IP V lære VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville I’ ( SUBJ) NP deltagerne I’ ( ADJUNCT) ADV dessverre IP ( OBJ) NP XP ( SUBJ) I' ( ADJUNCT). . . XP ADV* VP' ( SUBJ) ( ADJUNCT) S • SPEC of IP can also host the • Hence two rules in the same functional domain introduce subjects: • Functional uniqueness prevents the occurrence of subjects in both positions at once. N syntaks
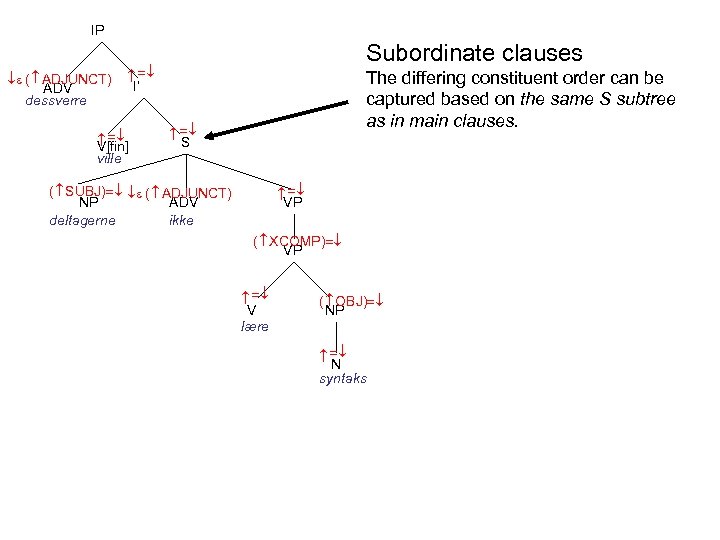 IP I’ S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville The differing constituent order can be captured based on the same S subtree as in main clauses. ( ADJUNCT) ADV dessverre Subordinate clauses
IP I’ S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville The differing constituent order can be captured based on the same S subtree as in main clauses. ( ADJUNCT) ADV dessverre Subordinate clauses
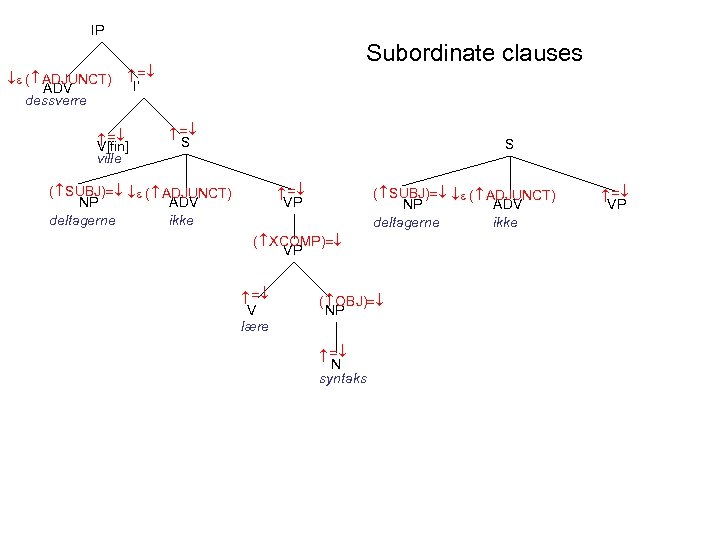 IP I’ S S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP ( OBJ) NP N syntaks V lære ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke V[fin] ville VP ( ADJUNCT) ADV dessverre Subordinate clauses
IP I’ S S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP ( OBJ) NP N syntaks V lære ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke V[fin] ville VP ( ADJUNCT) ADV dessverre Subordinate clauses
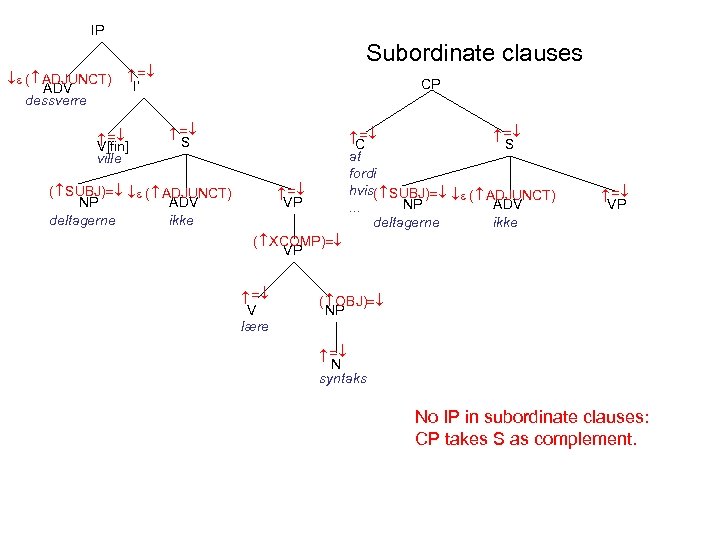 IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke VP V lære ( OBJ) NP N syntaks ( XCOMP) VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement.
IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke VP V lære ( OBJ) NP N syntaks ( XCOMP) VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement.
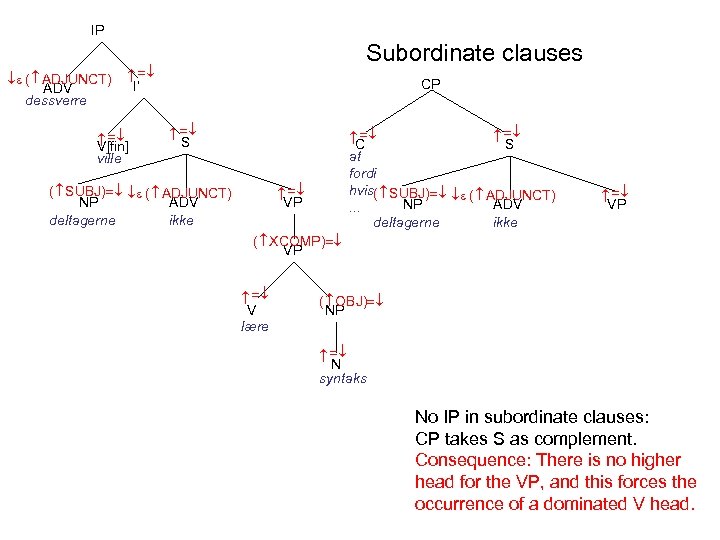 IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke VP V lære ( OBJ) NP N syntaks ( XCOMP) VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement. Consequence: There is no higher head for the VP, and this forces the occurrence of a dominated V head.
IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke VP V lære ( OBJ) NP N syntaks ( XCOMP) VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement. Consequence: There is no higher head for the VP, and this forces the occurrence of a dominated V head.
 IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( OBJ) NP V lære ( XCOMP) VP VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement. Consequence: There is no higher head for the VP, and this forces the occurrence of a dominated V head.
IP I’ CP C S at fordi hvis( SUBJ) ( ADJUNCT) NP ADV. . . deltagerne ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( OBJ) NP V lære ( XCOMP) VP VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke S V[fin] ville ( ADJUNCT) ADV dessverre Subordinate clauses No IP in subordinate clauses: CP takes S as complement. Consequence: There is no higher head for the VP, and this forces the occurrence of a dominated V head.
 S in main and subordinate clauses have similar scrambling possibilities: Main: Dessverre vil [S deltagerne ikke [VP lære syntaks]]] Dessverre vil [S ikke deltagerne [VP lære syntaks]]] Subordinate: hvis [S deltagerne ikke [VP vil [VP lære syntaks]]] hvis [S ikke deltagerne [VP vil [VP lære syntaks]]]
S in main and subordinate clauses have similar scrambling possibilities: Main: Dessverre vil [S deltagerne ikke [VP lære syntaks]]] Dessverre vil [S ikke deltagerne [VP lære syntaks]]] Subordinate: hvis [S deltagerne ikke [VP vil [VP lære syntaks]]] hvis [S ikke deltagerne [VP vil [VP lære syntaks]]]
 Main clause word order is also possible in subordinate clauses: Kari sa at hun var ikke syk
Main clause word order is also possible in subordinate clauses: Kari sa at hun var ikke syk
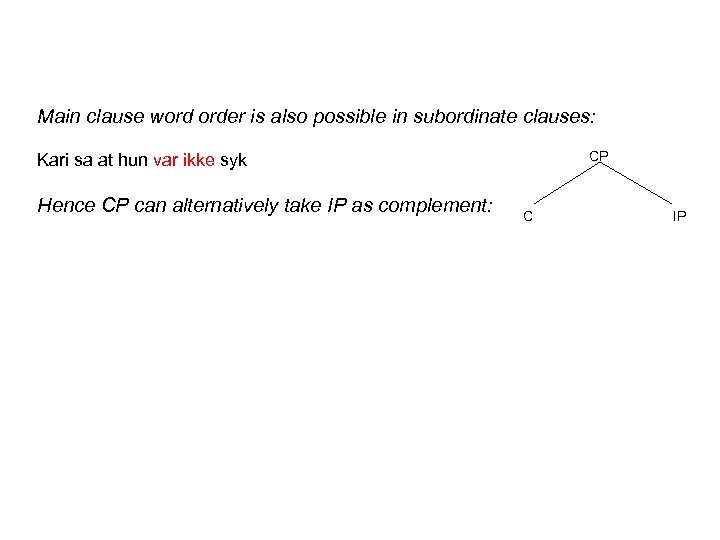 Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C IP
Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C IP
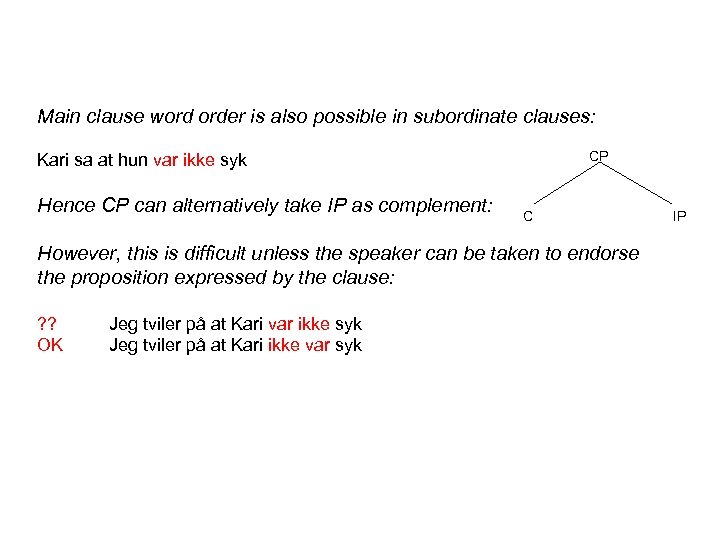 Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C However, this is difficult unless the speaker can be taken to endorse the proposition expressed by the clause: ? ? OK Jeg tviler på at Kari var ikke syk Jeg tviler på at Kari ikke var syk IP
Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C However, this is difficult unless the speaker can be taken to endorse the proposition expressed by the clause: ? ? OK Jeg tviler på at Kari var ikke syk Jeg tviler på at Kari ikke var syk IP
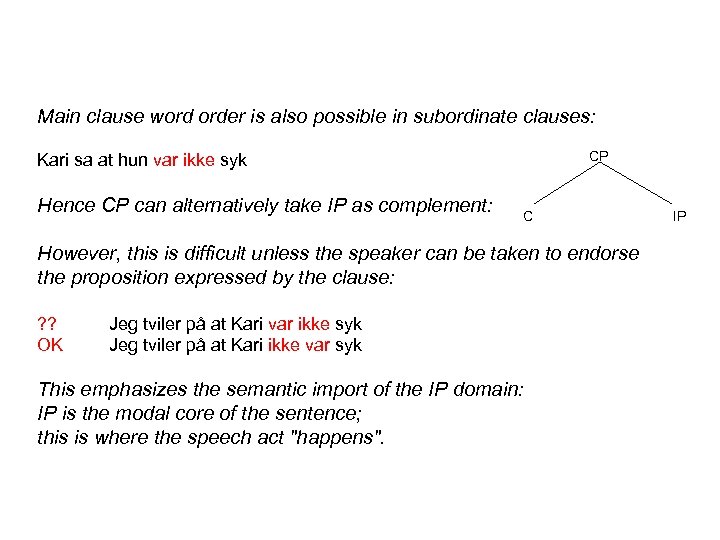 Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C However, this is difficult unless the speaker can be taken to endorse the proposition expressed by the clause: ? ? OK Jeg tviler på at Kari var ikke syk Jeg tviler på at Kari ikke var syk This emphasizes the semantic import of the IP domain: IP is the modal core of the sentence; this is where the speech act "happens". IP
Main clause word order is also possible in subordinate clauses: CP Kari sa at hun var ikke syk Hence CP can alternatively take IP as complement: C However, this is difficult unless the speaker can be taken to endorse the proposition expressed by the clause: ? ? OK Jeg tviler på at Kari var ikke syk Jeg tviler på at Kari ikke var syk This emphasizes the semantic import of the IP domain: IP is the modal core of the sentence; this is where the speech act "happens". IP
 Long-distance dependencies and Functional Uncertainty
Long-distance dependencies and Functional Uncertainty
![Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-104.jpg) Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( SUBJ) NP deltagerne
Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( SUBJ) NP deltagerne
![Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-105.jpg) Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( SUBJ) NP deltagerne
Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville ( SUBJ) NP deltagerne
![Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-106.jpg) Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. IP I’ NP syntaks V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. IP I’ NP syntaks V[fin] ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
![Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-107.jpg) Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. Will these equations do? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization The annotation ( SUBJ) on [SPEC, IP] should be replaced with a set of alternatives to handle topicalization. Let us topicalize the object as illustration. Will these equations do? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
 Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
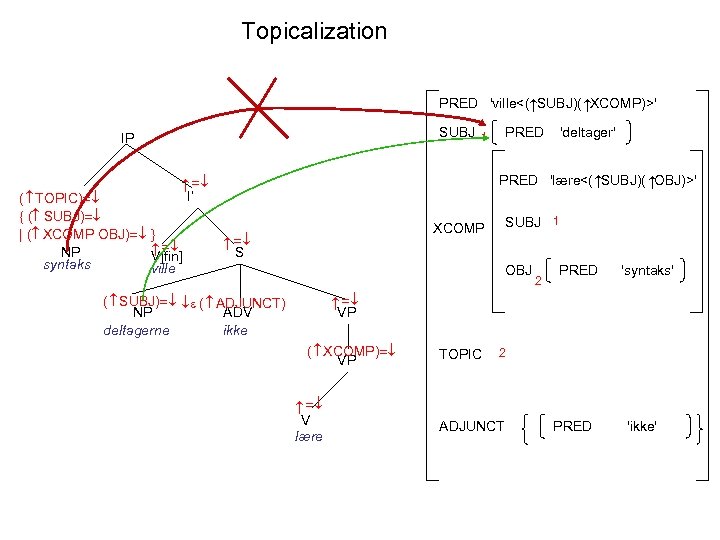 Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
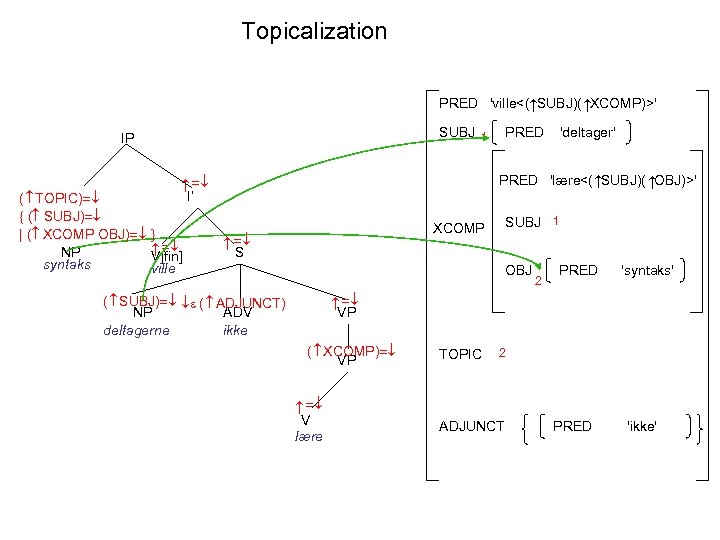 Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
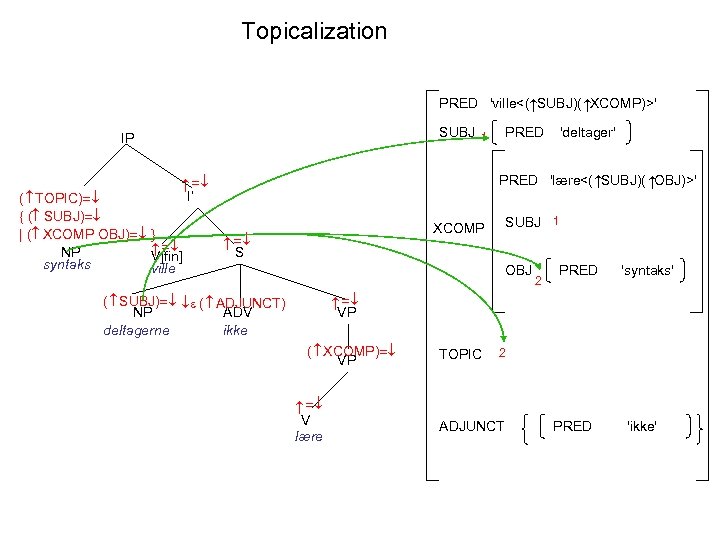 Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
Topicalization PRED 'ville<( SUBJ)( XCOMP)>' 'deltager' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 ADJUNCT PRED 'ikke'
 Topicalization PRED 'ville<( SUBJ)( XCOMP)>' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 The equations work for this sentence. But what about the following? 'deltager' ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP ADJUNCT PRED 'ikke'
Topicalization PRED 'ville<( SUBJ)( XCOMP)>' PRED 'lære<( SUBJ)( OBJ)>' I’ SUBJ 1 XCOMP S OBJ 2 PRED 'syntaks' VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære TOPIC 2 The equations work for this sentence. But what about the following? 'deltager' ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville PRED SUBJ 1 IP ADJUNCT PRED 'ikke'
![[Syntaks lærte deltagerne] [Syntaks sa Kari [at deltagerne ikke lærte]] [Syntaks ville deltagerne [prøve [Syntaks lærte deltagerne] [Syntaks sa Kari [at deltagerne ikke lærte]] [Syntaks ville deltagerne [prøve](https://present5.com/presentation/a0e4c9b3c7612fbb471cd78e24a9ccb2/image-113.jpg) [Syntaks lærte deltagerne] [Syntaks sa Kari [at deltagerne ikke lærte]] [Syntaks ville deltagerne [prøve [å lære]]] [Syntaks må da deltagerne [ha [kunnet [ville lære]]]] [Syntaks vil Kari [ha [sagt [at deltagerne ikke kan [ha [villet lære]]]]]] http: //iness. uib. no/xle-web
[Syntaks lærte deltagerne] [Syntaks sa Kari [at deltagerne ikke lærte]] [Syntaks ville deltagerne [prøve [å lære]]] [Syntaks må da deltagerne [ha [kunnet [ville lære]]]] [Syntaks vil Kari [ha [sagt [at deltagerne ikke kan [ha [villet lære]]]]]] http: //iness. uib. no/xle-web
 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
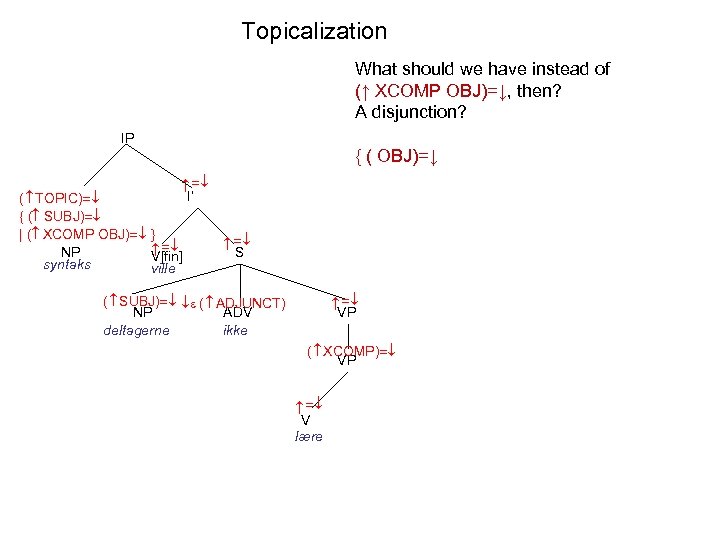 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
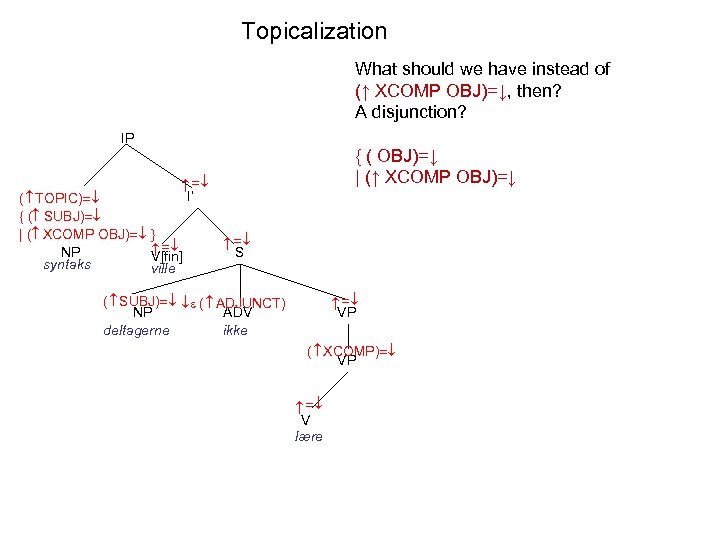 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
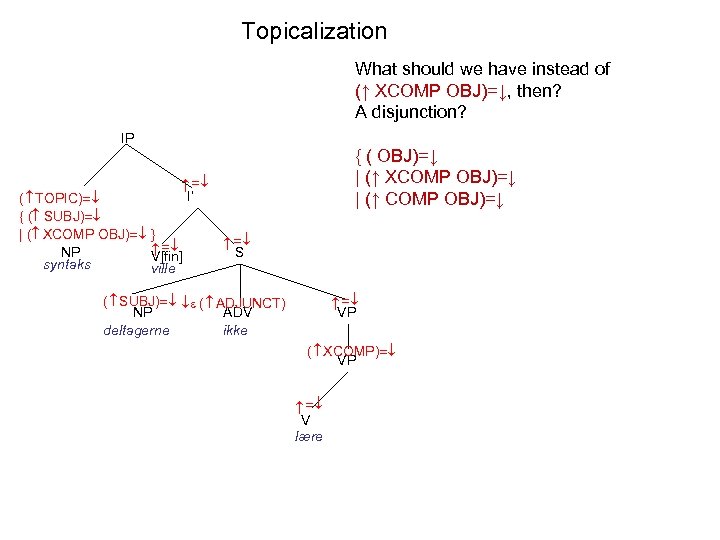 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
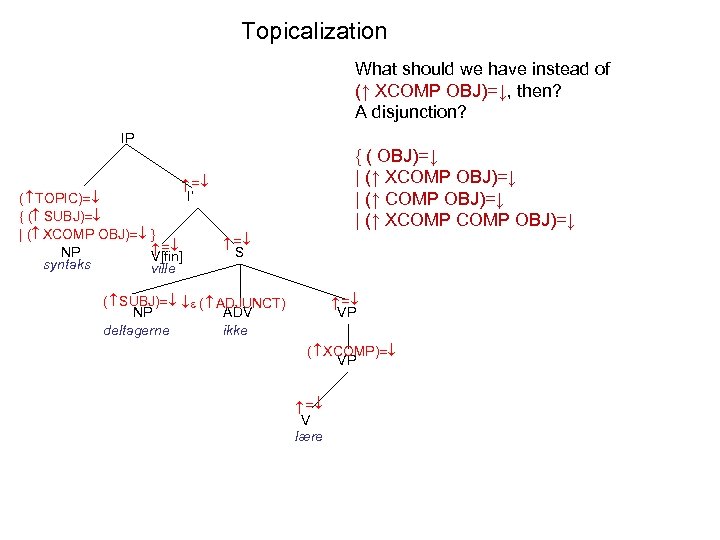
 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP XCOMP OBJ)=↓ I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
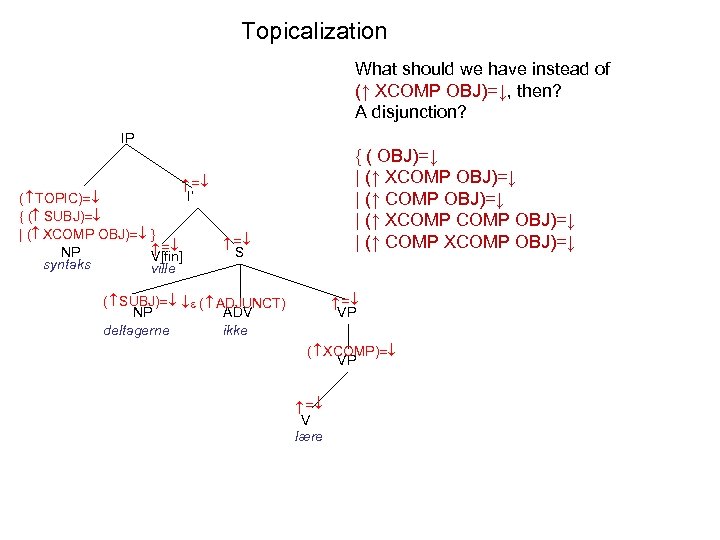
 Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP XCOMP OBJ)=↓ | (↑ XCOMP OBJ)=↓ |. . . } VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
Topicalization What should we have instead of (↑ XCOMP OBJ)=↓, then? A disjunction? IP I’ ( TOPIC) { ( SUBJ) | ( XCOMP OBJ) NP V[fin] syntaks ville S { ( OBJ)=↓ | (↑ XCOMP OBJ)=↓ | (↑ COMP XCOMP OBJ)=↓ | (↑ XCOMP OBJ)=↓ |. . . } VP ( SUBJ) ( ADJUNCT) NP ADV deltagerne ikke ( XCOMP) VP V lære
 We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . .
We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . .
 We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . . SUBJ XCOMP SUBJ COMP XCOMP SUBJ XCOMP SUBJ. . .
We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . . SUBJ XCOMP SUBJ COMP XCOMP SUBJ XCOMP SUBJ. . .
 We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . . SUBJ XCOMP SUBJ COMP XCOMP SUBJ XCOMP SUBJ. . . In other words, we are faced with a language
We are faced with an infinite number of alternative strings; OBJ XCOMP OBJ COMP XCOMP OBJ XCOMP OBJ. . . SUBJ XCOMP SUBJ COMP XCOMP SUBJ XCOMP SUBJ. . . In other words, we are faced with a language
 This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. .
This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. .
 This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ }.
This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ }.
 This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently.
This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently.
 This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently. Allowing regular expressions in constraint equations, enables them to specify sets of attribute paths rather than single paths: (↑{ COMP | XCOMP }* {SUBJ | OBJ }) =↓
This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently. Allowing regular expressions in constraint equations, enables them to specify sets of attribute paths rather than single paths: (↑{ COMP | XCOMP }* {SUBJ | OBJ }) =↓
 This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently. Allowing regular expressions in constraint equations, enables them to specify sets of attribute paths rather than single paths: (↑{ COMP | XCOMP }* {SUBJ | OBJ }) =↓ This constraint equation is satisfied if there is at least one path in the set which maks it true.
This language is very simple: it consists of all strings that begin with any number og COMPs and XCOMPs (including zero) in any order, and ends with either SUBJ or OBJ. It can be captured by a Regular Expression: { COMP | XCOMP }* {SUBJ | OBJ } This means that it is a Finite State Language, which can be parsed very efficiently. Allowing regular expressions in constraint equations, enables them to specify sets of attribute paths rather than single paths: (↑{ COMP | XCOMP }* {SUBJ | OBJ }) =↓ This constraint equation is satisfied if there is at least one path in the set which maks it true.
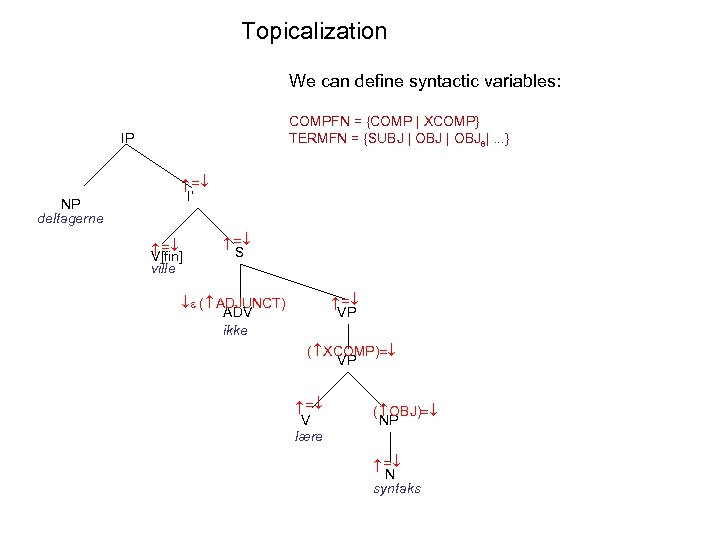 Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville NP deltagerne
Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville NP deltagerne
 Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville NP deltagerne
Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP I’ S VP ( ADJUNCT) ADV ikke ( XCOMP) VP V lære ( OBJ) NP N syntaks V[fin] ville NP deltagerne
 Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP This simplifies the equations I’ ( TOP) ( COMPFN* TERMFN) NP deltagerne V[fin] ville S VP ( ADJUNCT) ADV ikke ( XCOMP) VP ( OBJ) NP N syntaks V lære COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . }
Topicalization We can define syntactic variables: COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . } IP This simplifies the equations I’ ( TOP) ( COMPFN* TERMFN) NP deltagerne V[fin] ville S VP ( ADJUNCT) ADV ikke ( XCOMP) VP ( OBJ) NP N syntaks V lære COMPFN = {COMP | XCOMP} TERMFN = {SUBJ | OBJ |. . . }
 F-structures and Dependency Structures
F-structures and Dependency Structures
 From the PROIEL Project: A sentence from the Gothic Bible (Mark 1. 8):
From the PROIEL Project: A sentence from the Gothic Bible (Mark 1. 8):
 From the PROIEL Project: A sentence from the Gothic Bible (Mark 1. 8): Norwegian translation: For jeg døper dere i vann, men han døper dere i hellig ånd.
From the PROIEL Project: A sentence from the Gothic Bible (Mark 1. 8): Norwegian translation: For jeg døper dere i vann, men han døper dere i hellig ånd.
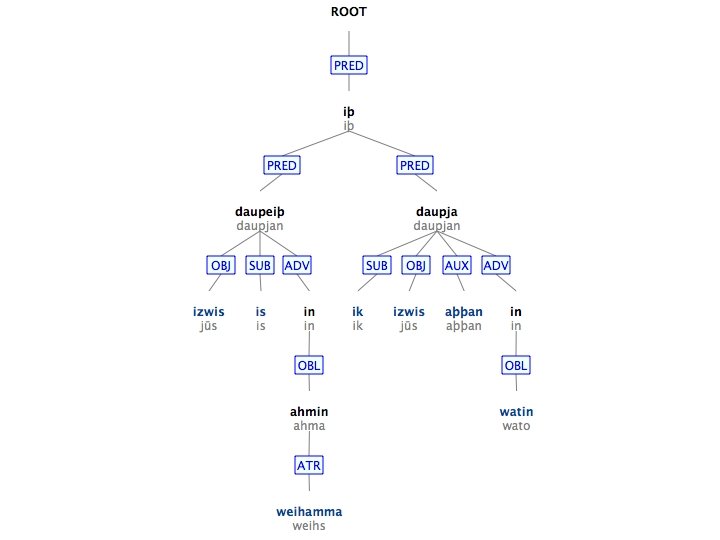
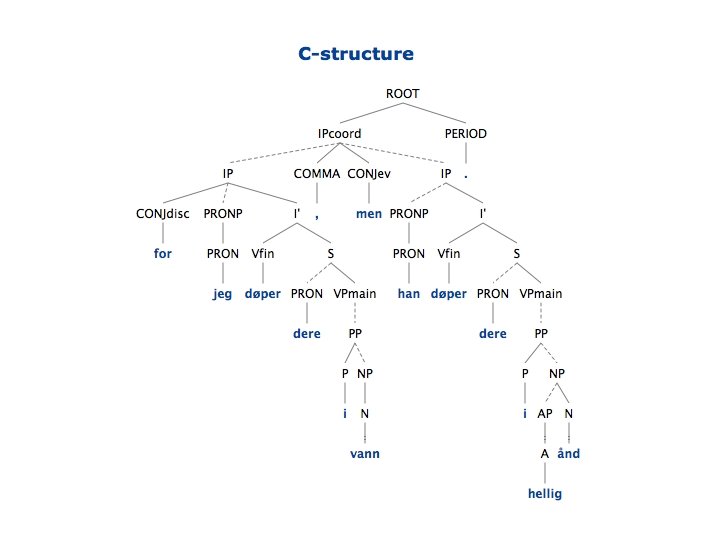

 ‘PREDs only’ version:
‘PREDs only’ version:
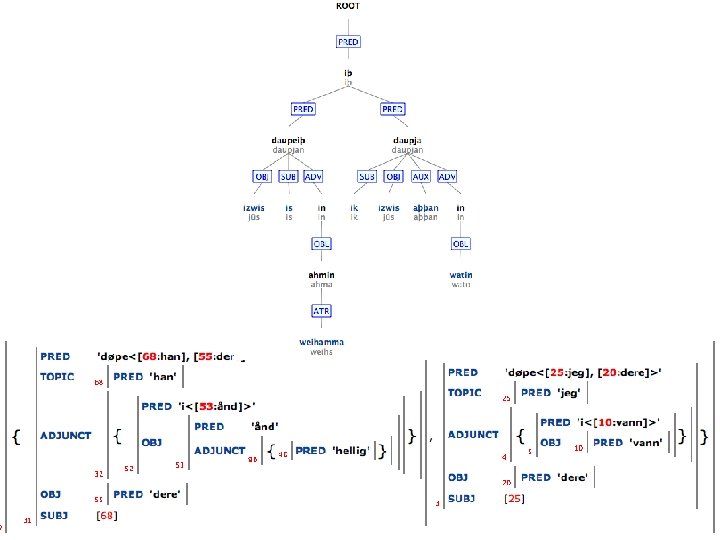
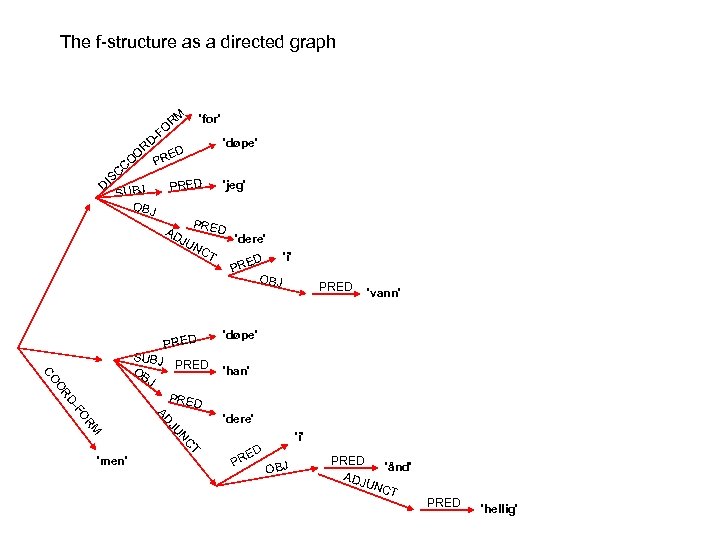 The f-structure as a directed graph RM O F DR O ED O PR C SC DI UBJ S OBJ 'for' 'døpe' PRED AD PRED JU D OR CO SUBJ OB J 'jeg' NC T PRED 'dere' 'i' ED PR OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
The f-structure as a directed graph RM O F DR O ED O PR C SC DI UBJ S OBJ 'for' 'døpe' PRED AD PRED JU D OR CO SUBJ OB J 'jeg' NC T PRED 'dere' 'i' ED PR OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
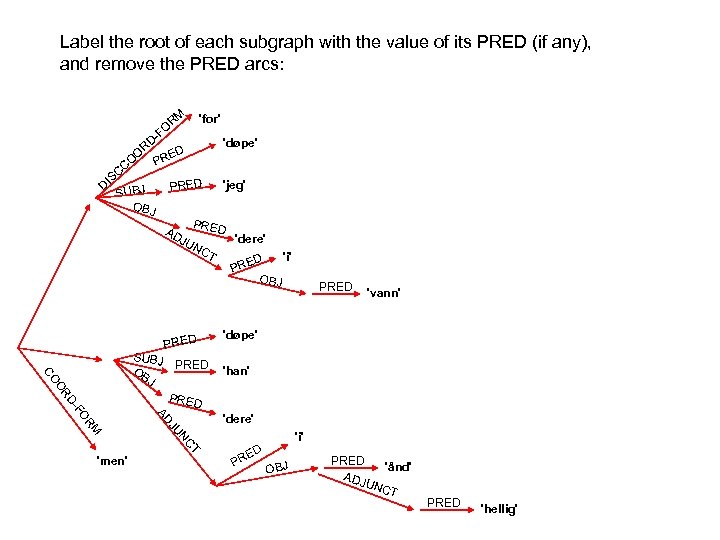 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O ED O PR C SC DI UBJ S OBJ 'for' 'døpe' PRED AD PRED JU D OR CO SUBJ OB J 'jeg' NC T PRED 'dere' 'i' ED PR OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O ED O PR C SC DI UBJ S OBJ 'for' 'døpe' PRED AD PRED JU D OR CO SUBJ OB J 'jeg' NC T PRED 'dere' 'i' ED PR OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
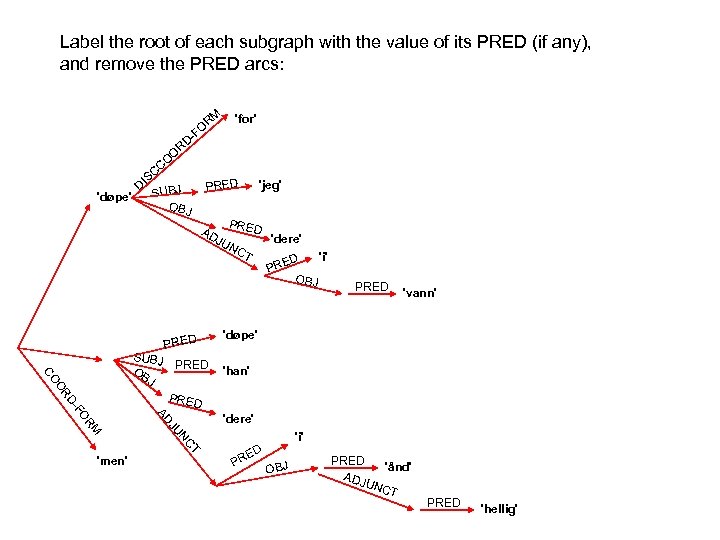 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' PRED AD PRED JU D OR CO SUBJ OB J PRED 'jeg' NC T 'dere' D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' PRED AD PRED JU D OR CO SUBJ OB J PRED 'jeg' NC T 'dere' D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
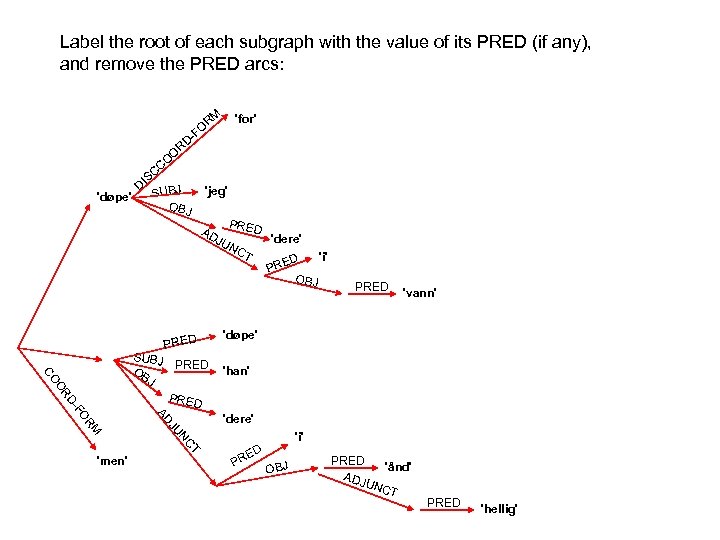 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD JU PRED D OR CO SUBJ OB J PRED NC T 'dere' D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD JU PRED D OR CO SUBJ OB J PRED NC T 'dere' D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T D OR CO SUBJ OB J PRED D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T D OR CO SUBJ OB J PRED D E PR OBJ 'i' PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
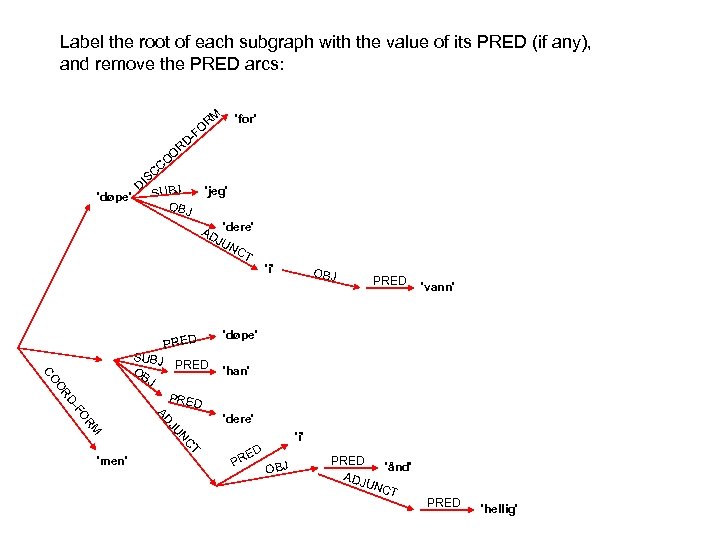 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' D OR CO SUBJ OB J PRED OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' D OR CO SUBJ OB J PRED OBJ PRED 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' D OR CO SUBJ OB J PRED OBJ 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' D OR CO SUBJ OB J PRED OBJ 'vann' 'døpe' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
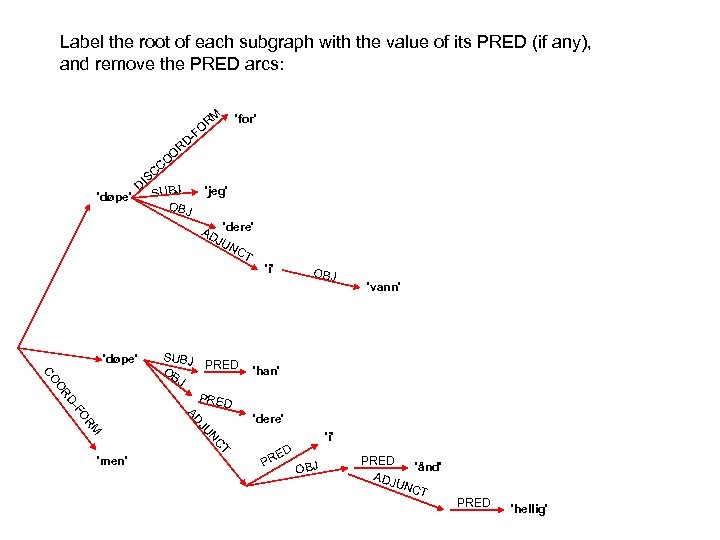 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OB J PRED OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OB J PRED OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
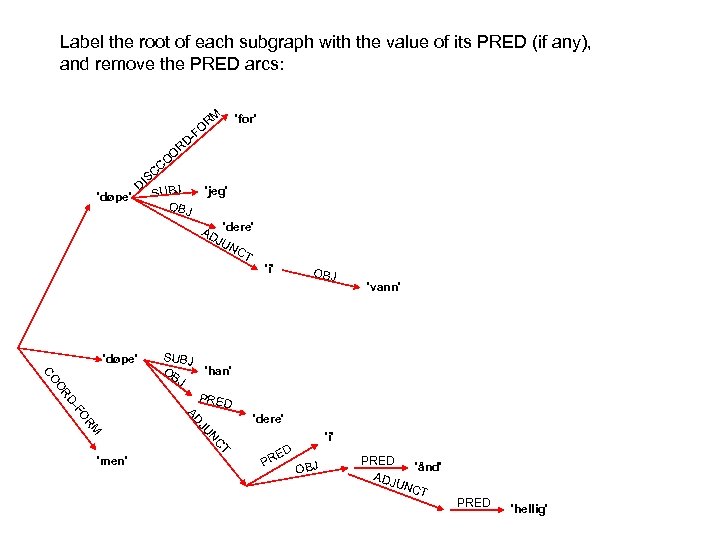 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F PRED 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
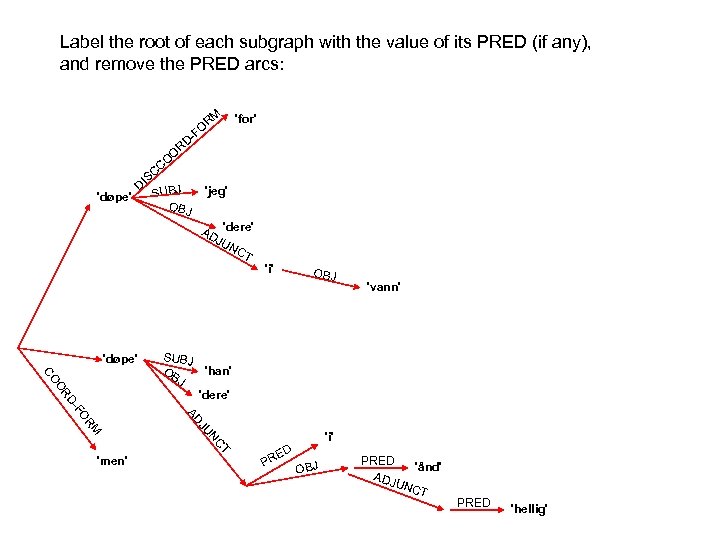 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' 'i' PR ED OBJ PRED ADJ U 'ånd' NCT PRED 'hellig'
 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' PRED ADJ U 'ånd' NCT PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' PRED ADJ U 'ånd' NCT PRED 'hellig'
 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T PRED 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T PRED 'hellig'
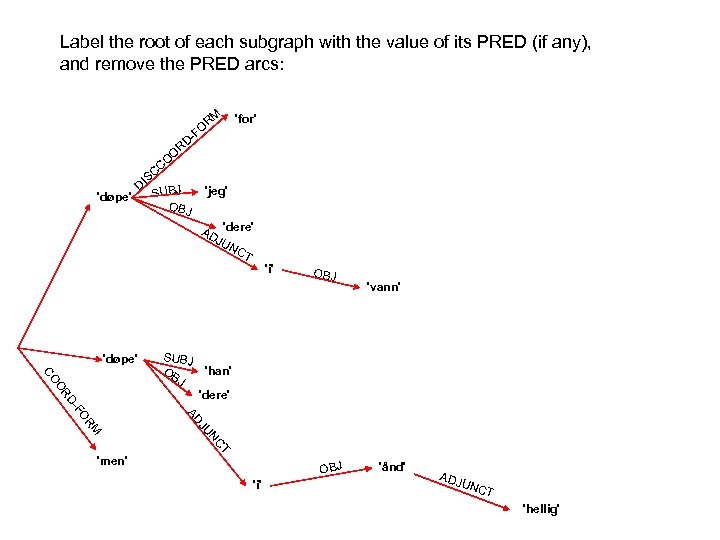 Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T 'hellig'
Label the root of each subgraph with the value of its PRED (if any), and remove the PRED arcs: RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T 'hellig'
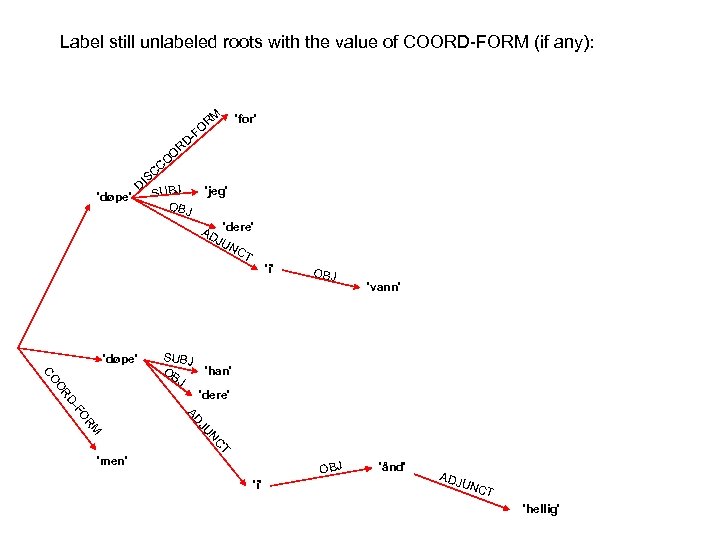 Label still unlabeled roots with the value of COORD-FORM (if any): RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T 'hellig'
Label still unlabeled roots with the value of COORD-FORM (if any): RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'døpe' D OR CO SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD RM O -F 'men' OBJ 'i' 'ånd' ADJ UNC T 'hellig'
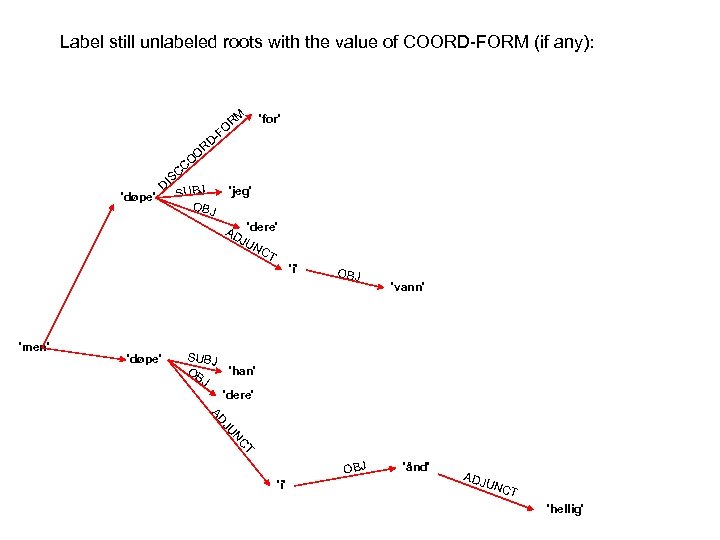 Label still unlabeled roots with the value of COORD-FORM (if any): RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'men' 'døpe' SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD OBJ 'i' 'ånd' ADJ UNC T 'hellig'
Label still unlabeled roots with the value of COORD-FORM (if any): RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'men' 'døpe' SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD OBJ 'i' 'ånd' ADJ UNC T 'hellig'
 Turn it 90 degrees. . . RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'men' 'døpe' SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD OBJ 'i' 'ånd' ADJ UNC T 'hellig'
Turn it 90 degrees. . . RM O F DR O O CC S DI UBJ S 'døpe' OBJ 'for' 'jeg' AD 'dere' JU NC T 'i' 'men' 'døpe' SUBJ OBJ 'vann' 'han' 'dere' CT UN J AD OBJ 'i' 'ånd' ADJ UNC T 'hellig'
 Turn it 90 degrees. . .
Turn it 90 degrees. . .
 and compare:
and compare:


