a8d89783312f5f06d2a16f0458a9d44c.ppt
- Количество слайдов: 67
 The pricing of forward and futures contracts
The pricing of forward and futures contracts
 Outline • Spot and futures prices for non-dividend paying investment assets • Spot and futures prices for investment assets paying a known income • Spot and futures prices for investment assets paying a known yield/return • Spot and futures prices for commodities with storage costs • Spot and futures prices for consumption commodities with storage costs • The cost of carry • The valuation of forward contracts
Outline • Spot and futures prices for non-dividend paying investment assets • Spot and futures prices for investment assets paying a known income • Spot and futures prices for investment assets paying a known yield/return • Spot and futures prices for commodities with storage costs • Spot and futures prices for consumption commodities with storage costs • The cost of carry • The valuation of forward contracts
 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
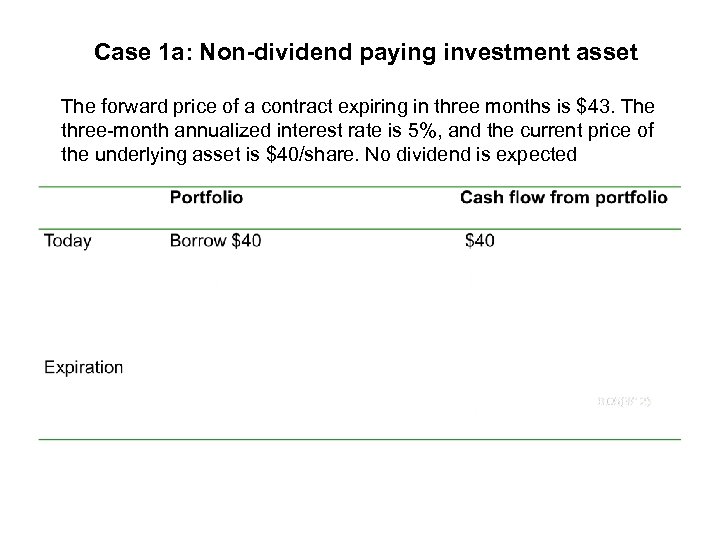 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
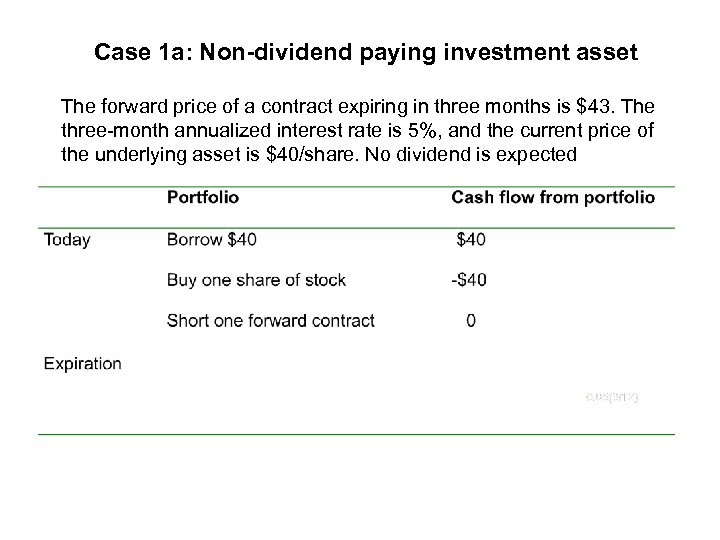 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
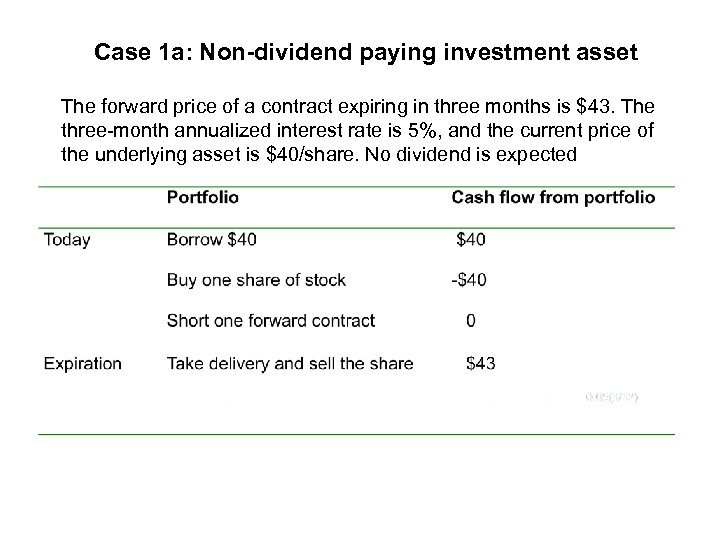 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
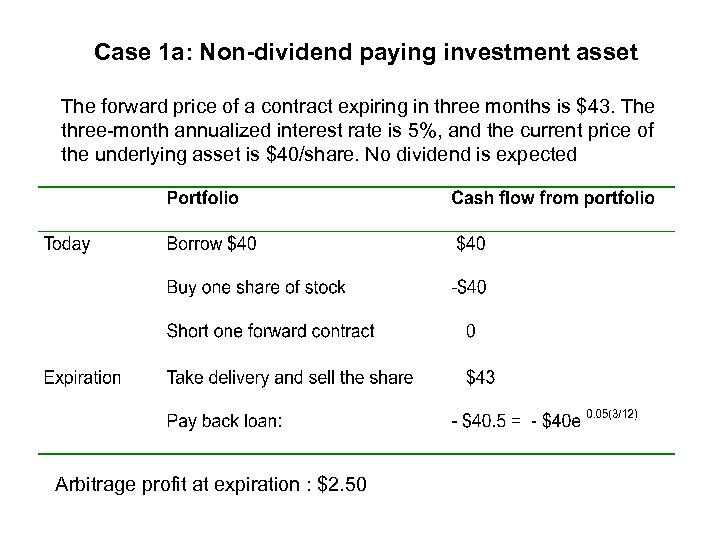 Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected Arbitrage profit at expiration : $2. 50
Case 1 a: Non-dividend paying investment asset The forward price of a contract expiring in three months is $43. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected Arbitrage profit at expiration : $2. 50
 Case 1 a: Implications Eventually, investors would bid up the stock price, and drive down the forward price
Case 1 a: Implications Eventually, investors would bid up the stock price, and drive down the forward price
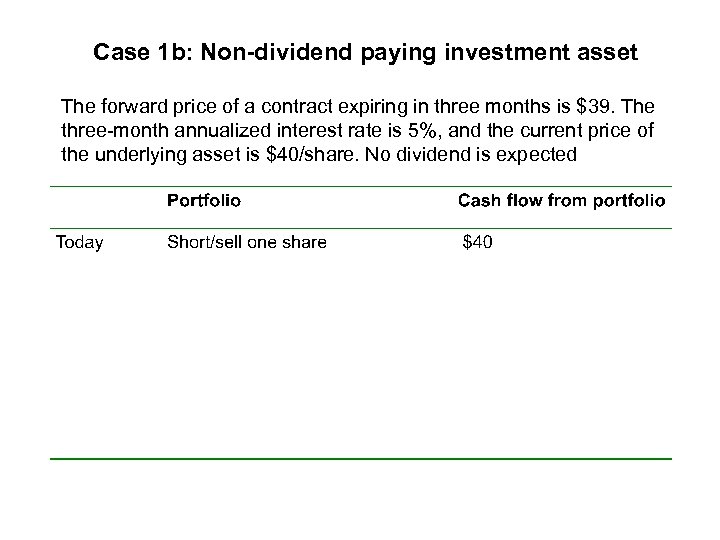 Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
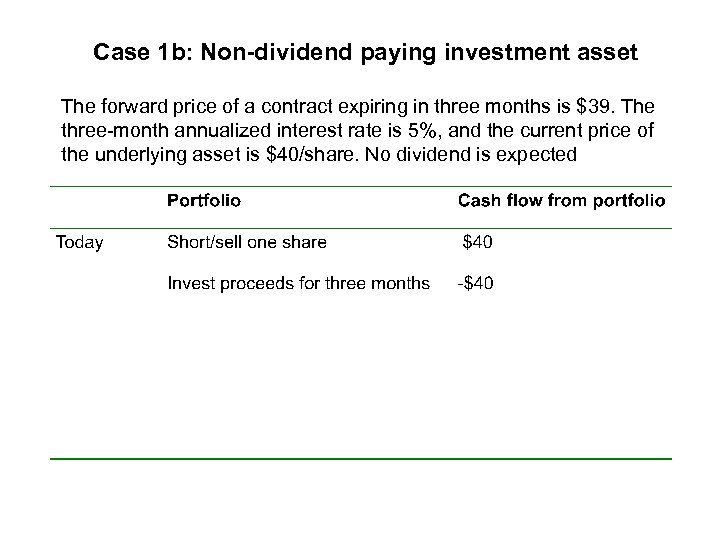 Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
 Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected
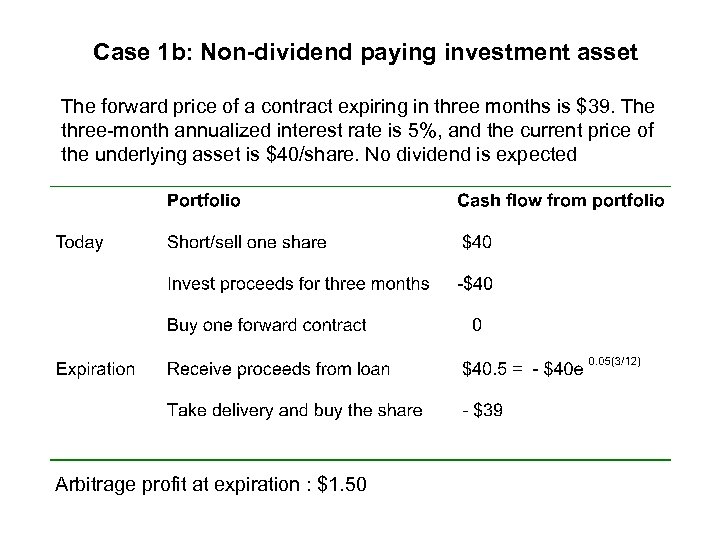 Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected Arbitrage profit at expiration : $1. 50
Case 1 b: Non-dividend paying investment asset The forward price of a contract expiring in three months is $39. The three-month annualized interest rate is 5%, and the current price of the underlying asset is $40/share. No dividend is expected Arbitrage profit at expiration : $1. 50
 Case 1 b: Implications Eventually, investors would drive down the stock price, and bid up the forward price
Case 1 b: Implications Eventually, investors would drive down the stock price, and bid up the forward price
 Relationship between spot and forward/futures prices for a non-dividend paying investment asset F 0 = S 0 er. T F 0 = forward/futures price today S 0 = underlying asset spot price today r = risk-free rate T = time to expiration
Relationship between spot and forward/futures prices for a non-dividend paying investment asset F 0 = S 0 er. T F 0 = forward/futures price today S 0 = underlying asset spot price today r = risk-free rate T = time to expiration
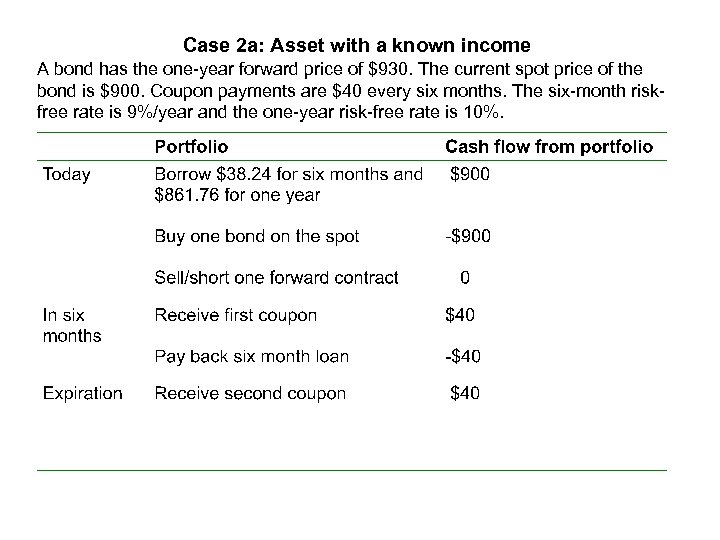
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%. Arbitrage profit at expiration : $17. 61
Case 2 a: Asset with a known income A bond has the one-year forward price of $930. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%. Arbitrage profit at expiration : $17. 61
 Case 2 a: Implication Eventually, investors would drive down the forward price, and bid up the spot price of the bond
Case 2 a: Implication Eventually, investors would drive down the forward price, and bid up the spot price of the bond
 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%.
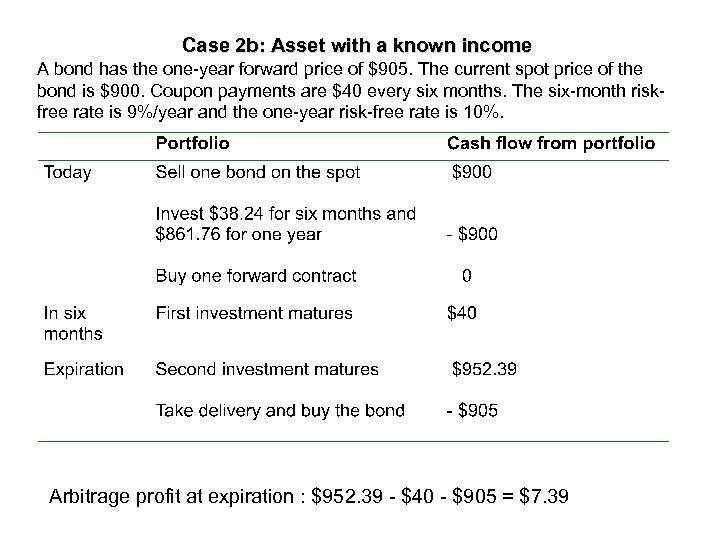 Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%. Arbitrage profit at expiration : $952. 39 - $40 - $905 = $7. 39
Case 2 b: Asset with a known income A bond has the one-year forward price of $905. The current spot price of the bond is $900. Coupon payments are $40 every six months. The six-month riskfree rate is 9%/year and the one-year risk-free rate is 10%. Arbitrage profit at expiration : $952. 39 - $40 - $905 = $7. 39
 Case 2 b: Implication Eventually, investors would drive down the spot price, and bid up the forward price of the bond
Case 2 b: Implication Eventually, investors would drive down the spot price, and bid up the forward price of the bond
 Relationship between spot and forward/futures prices for an investment asset providing a known income F 0 = (S 0 - PVincome)er. T In our example: PVincome = $40 e-(0. 09)(0. 5) + $40 e-(0. 1)
Relationship between spot and forward/futures prices for an investment asset providing a known income F 0 = (S 0 - PVincome)er. T In our example: PVincome = $40 e-(0. 09)(0. 5) + $40 e-(0. 1)
 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
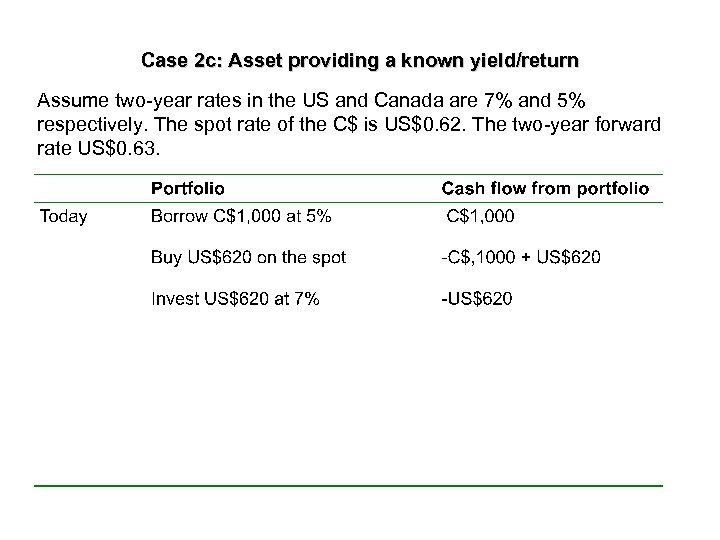 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
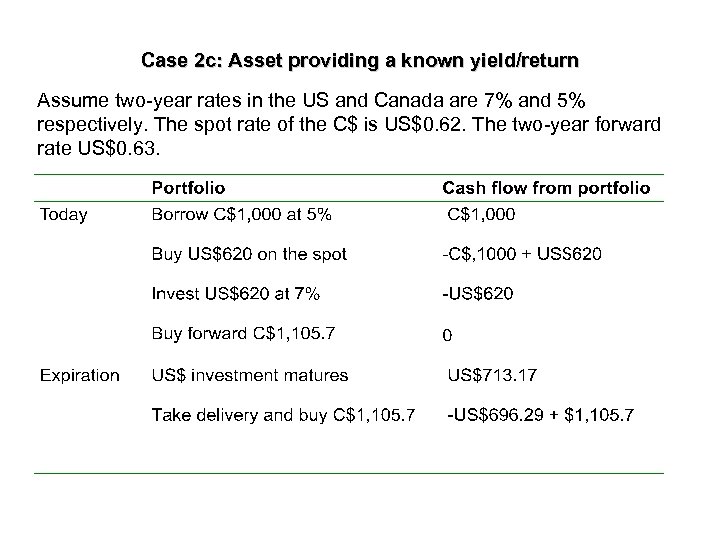 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63.
 Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63. Arbitrage profit = US$16. 91
Case 2 c: Asset providing a known yield/return Assume two-year rates in the US and Canada are 7% and 5% respectively. The spot rate of the C$ is US$0. 62. The two-year forward rate US$0. 63. Arbitrage profit = US$16. 91
 Case 2 c: Implication Eventually, investors would drive down the forward price and bid up the spot price of the US$
Case 2 c: Implication Eventually, investors would drive down the forward price and bid up the spot price of the US$
 Relationship between spot and forward/futures prices for an investment asset providing a known yield/return F 0 = S 0 e(r-q)T Where q is the known yield/return provided by the investment asset In case 2 c, q is the interest rate on the foreign currency.
Relationship between spot and forward/futures prices for an investment asset providing a known yield/return F 0 = S 0 e(r-q)T Where q is the known yield/return provided by the investment asset In case 2 c, q is the interest rate on the foreign currency.
 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year.
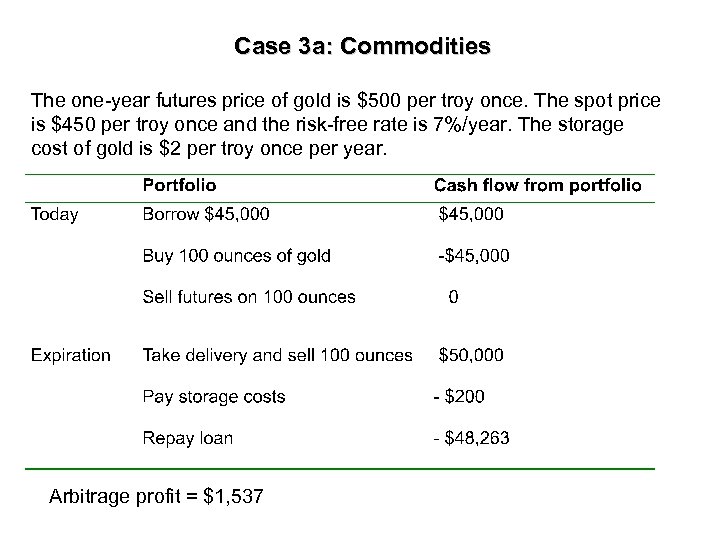 Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year. Arbitrage profit = $1, 537
Case 3 a: Commodities The one-year futures price of gold is $500 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year. Arbitrage profit = $1, 537
 Case 3 a: Implications In the long run, investors would bid up the spot price of gold and drive down its futures price.
Case 3 a: Implications In the long run, investors would bid up the spot price of gold and drive down its futures price.
 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
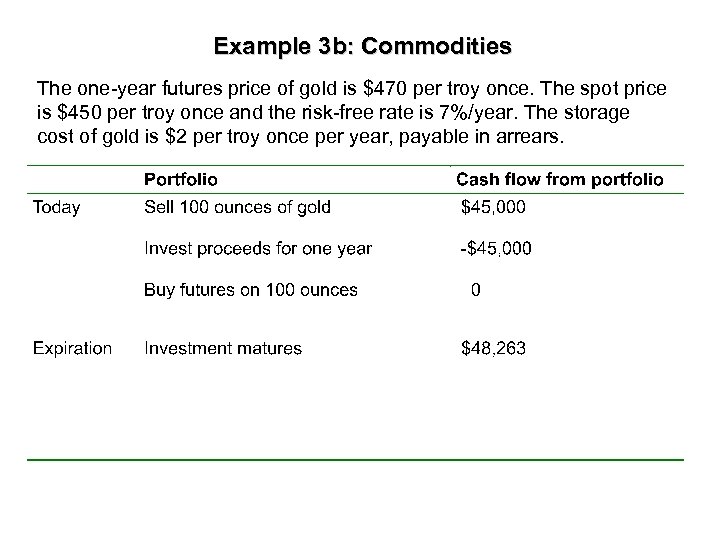 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears.
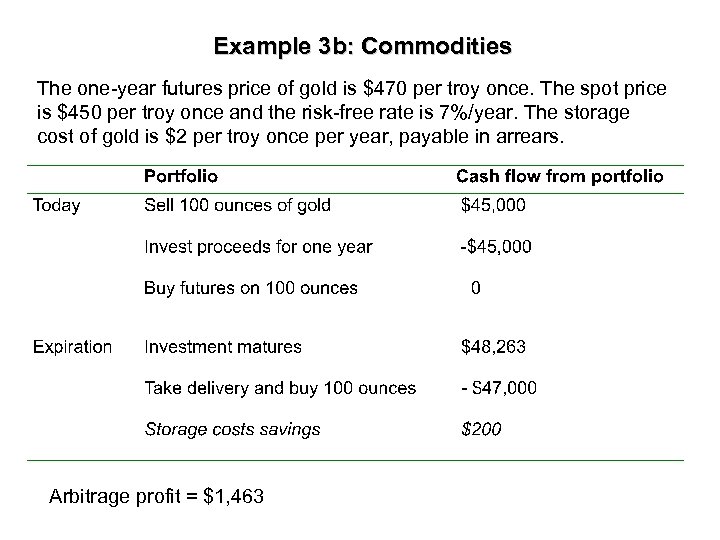 Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears. Arbitrage profit = $1, 463
Example 3 b: Commodities The one-year futures price of gold is $470 per troy once. The spot price is $450 per troy once and the risk-free rate is 7%/year. The storage cost of gold is $2 per troy once per year, payable in arrears. Arbitrage profit = $1, 463
 Case 3 b: Implications In the long run, investors would bid up the futures price of gold and drive down the spot price
Case 3 b: Implications In the long run, investors would bid up the futures price of gold and drive down the spot price
 Relationship between spot and forward/futures prices for an investment commodity with storage costs F 0 = (S 0 + U)er. T Where U = PV of storage costs (negative income). If the storage cost is proportional to the price of the asset, storage costs can be viewed as a negative yield: F 0 = S 0 e(r + u)T
Relationship between spot and forward/futures prices for an investment commodity with storage costs F 0 = (S 0 + U)er. T Where U = PV of storage costs (negative income). If the storage cost is proportional to the price of the asset, storage costs can be viewed as a negative yield: F 0 = S 0 e(r + u)T
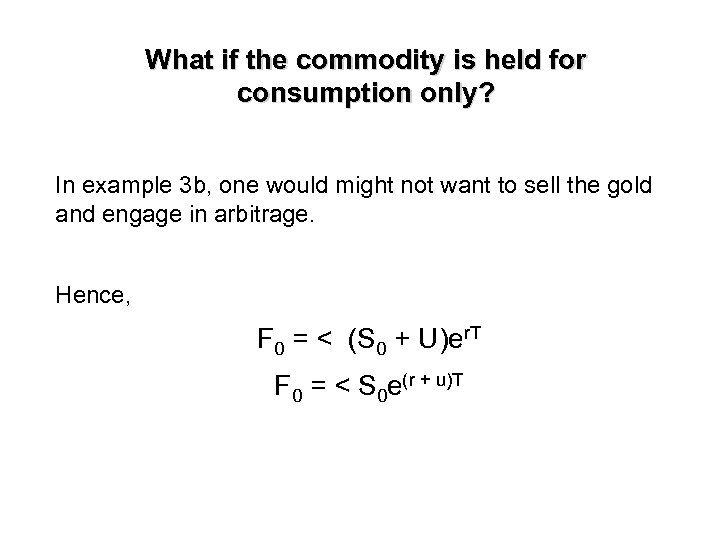 What if the commodity is held for consumption only? In example 3 b, one would might not want to sell the gold and engage in arbitrage. Hence, F 0 = < (S 0 + U)er. T F 0 = < S 0 e(r + u)T
What if the commodity is held for consumption only? In example 3 b, one would might not want to sell the gold and engage in arbitrage. Hence, F 0 = < (S 0 + U)er. T F 0 = < S 0 e(r + u)T
 Relationship between spot and forward/futures prices for a consumption commodity with storage costs F 0 = (S 0 + U)e(r - y)T or F 0 = S 0 e(r + u - y)T Where y is a fudge factor called convenience yield
Relationship between spot and forward/futures prices for a consumption commodity with storage costs F 0 = (S 0 + U)e(r - y)T or F 0 = S 0 e(r + u - y)T Where y is a fudge factor called convenience yield
 The cost of carry It measures the interest paid to finance the asset plus storage costs less income earned on the asset. For an investment asset paying no dividend cc = r For a stock index cc = q For a foreign currency cc = rf For a commodity with storage costs proportional to price cc = r + u
The cost of carry It measures the interest paid to finance the asset plus storage costs less income earned on the asset. For an investment asset paying no dividend cc = r For a stock index cc = q For a foreign currency cc = rf For a commodity with storage costs proportional to price cc = r + u
 The valuation of forward contracts What is the value of a forward contract at inception? Zero
The valuation of forward contracts What is the value of a forward contract at inception? Zero
 The valuation of forward contracts: Investment asset paying no dividend/income What is the value of a forward contract between inception and maturity? Long contract f = (F 0 - F)e-r. T f = S 0 - Fe-r. T Short contract f = (F - F 0)e-r. T f = Fe-r. T - S 0 Where F is the current forward price of the contract.
The valuation of forward contracts: Investment asset paying no dividend/income What is the value of a forward contract between inception and maturity? Long contract f = (F 0 - F)e-r. T f = S 0 - Fe-r. T Short contract f = (F - F 0)e-r. T f = Fe-r. T - S 0 Where F is the current forward price of the contract.
 The valuation of futures contracts What is the value of a futures contract between inception and maturity? At the end of each trading day, the value of futures is set back to zero as a result of marking-to-market.
The valuation of futures contracts What is the value of a futures contract between inception and maturity? At the end of each trading day, the value of futures is set back to zero as a result of marking-to-market.
 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary
 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary
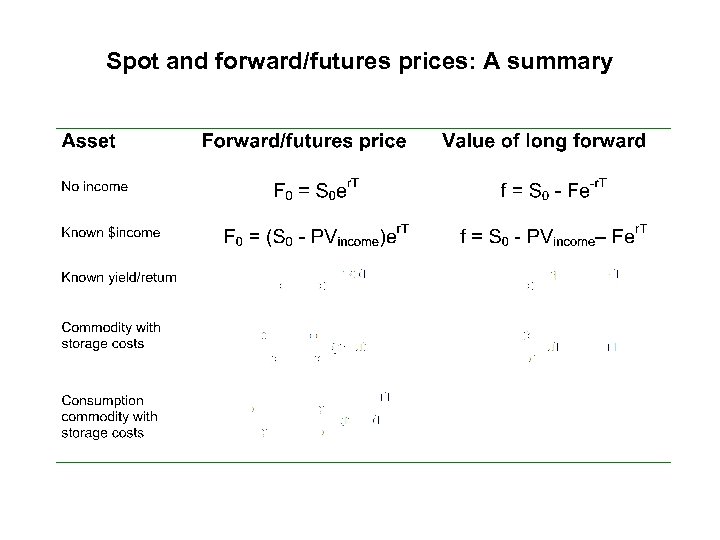 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary
 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary
 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary
 Spot and forward/futures prices: A summary
Spot and forward/futures prices: A summary


