The Physics of Molecular Motors fluctuations in

The Physics of Molecular Motors • fluctuations in small engines • … and the II Law of Thermodynamics • noise rectification mechanisms RD Astumian, Sci. Am. , July 2001, 57 P. Hanggi and F. M. , Rev. Mod. Phys. , 81 (2009) 387

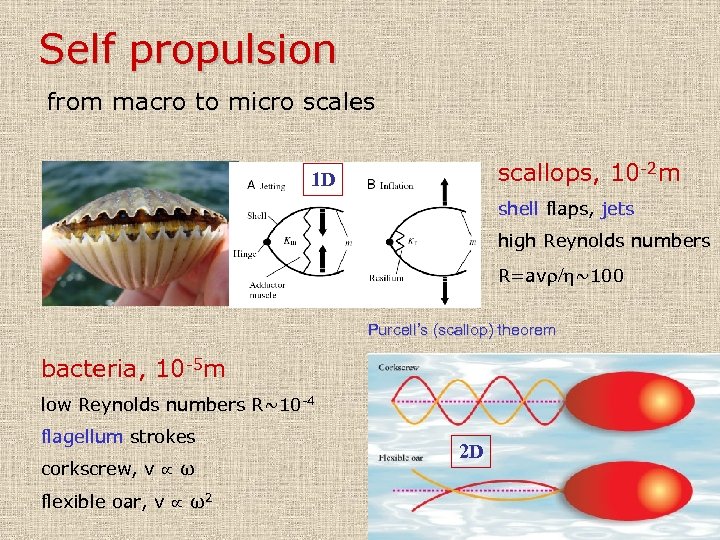Self propulsion from macro to micro scales scallops, 10 -2 m 1 D shell flaps, jets high Reynolds numbers R=avr/h~100 Purcell’s (scallop) theorem bacteria, 10 -5 m low Reynolds numbers R~10 -4 flagellum strokes corkscrew, v ω flexible oar, v ω2 2 D

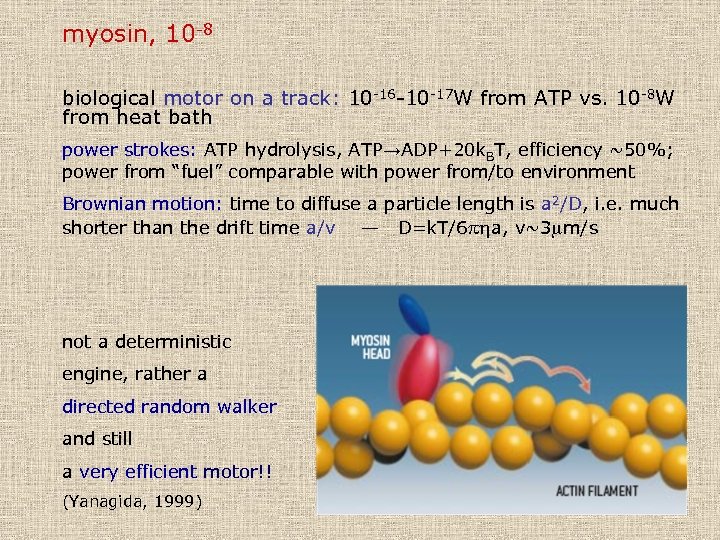myosin, 10 -8 biological motor on a track: 10 -16 -10 -17 W from ATP vs. 10 -8 W from heat bath power strokes: ATP hydrolysis, ATP→ADP+20 k. BT, efficiency ~50%; power from “fuel” comparable with power from/to environment Brownian motion: time to diffuse a particle length is a 2/D, i. e. much shorter than the drift time a/v — D=k. T/6 pha, v~3 mm/s not a deterministic engine, rather a directed random walker and still a very efficient motor!! (Yanagida, 1999)

Rectifying thermal fluctuations? unbalanced wheel L. da Vinci SPRING pawl ratchet R. Feynman PAWL VANE RATCHET noise harvesting, noise-powered small devices

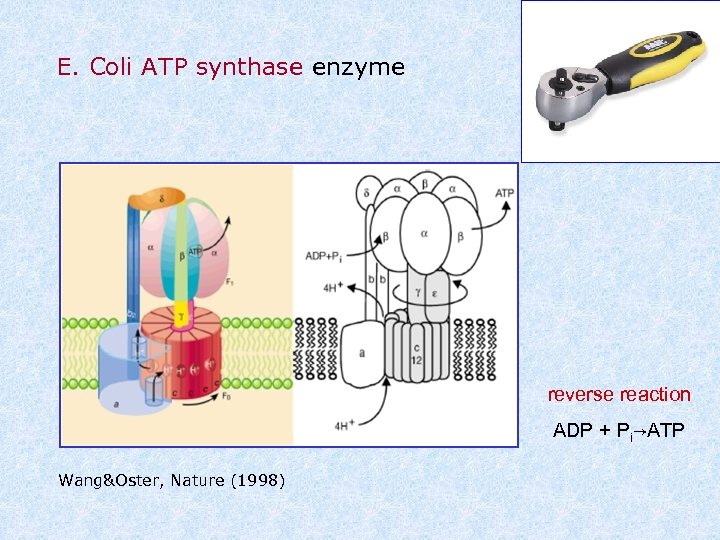E. Coli ATP synthase enzyme reverse reaction ADP + Pi→ATP Wang&Oster, Nature (1998)

impossible (at equilibrium)! The Feynman Lectures on Physics, I-46 assign ratchet and vane e temperatures T 1 and T 2; at equilibrium T 1 = T 2 t angular velocity of ratchet t W rectification T 1 = T 2

Maxwell daemon If an automated devices doesn’t work, what about an intelligent one? J C Maxwell . . . if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, …. will raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics (1871).

also impossible, but … M. Smoluchowski (1914): No automatic, permanently effective perpetual motion machine can violate the II Law by taking advantage of statistical fluctuations. Such device might perhaps function if operated by intelligent beings. W. H. Zurek (1989): The II Law is safe from intelligent beings as long as their abilities to process information are subject to the same laws as those of universal Turing machines P. Curie (1894): Rectification of statistical fluctuations requires simultaneous breaking of spatial and time symmetry

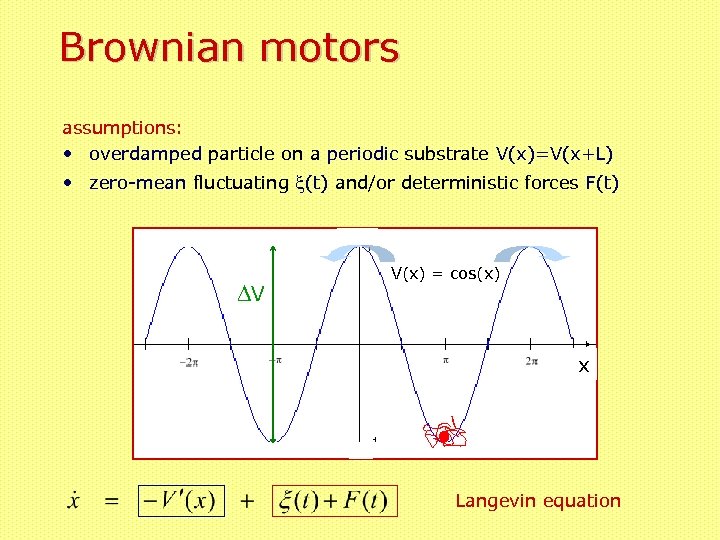Brownian motors assumptions: • overdamped particle on a periodic substrate V(x)=V(x+L) • zero-mean fluctuating x(t) and/or deterministic forces F(t) DV V(x) = cos(x) x Langevin equation

different non-equilibrium options → a. symmetric substrate: V(-x) V(x) 1. x(t) Gaussian, stationary and white (equilibrium noise) ‹x(t)x(0)›=2 Dd(t); F(t)=F 1 cos(W 1 t) sinusoidal signal, F(-t) -F(t) 2. x(t) Gaussian, stationary and colored, (non-equilibrium noise) ‹x(t)x(0)›=(D/t)exp(-|t|/t) [w/ or w/o a sinusoidal signal F(t)] no transport current,

harmonic mixing F(t) bi-harmonic signal, F(t) = F 1 cos(W 1 t+f 1) + F 2 cos(W 2 t+f 2); commensurate frequencies, W 1/W 2 = m/n w/ or w/o the noise x(t) rectification due to the interplay of nonlinearity and drive asymmetry F(-t) -F(t) biased, we cheated! F(t)

ratchet effect: rocked, pulsated, thermal b. asymmetric substrate: V(-x) ≠ V(x) 1. rocked: F(t) additive sinusoidal signal, F(t)=F 1 cos(W 1 t), w/ or w/o noise; 2. pulsated: x(t) Gaussian and white, ‹x(t)x(0)›=2 Dd(t); F(t) multiplicative sinusoidal signal, i. e. modulates substrate amplitude, F(t)=e. V(x)cos(Wt) 3. thermal: w/ or w/o drive; x(t) Gaussian and colored, ‹x(t)x(0)›=(D/t)exp(-|t|/t); net transport current is the rule!

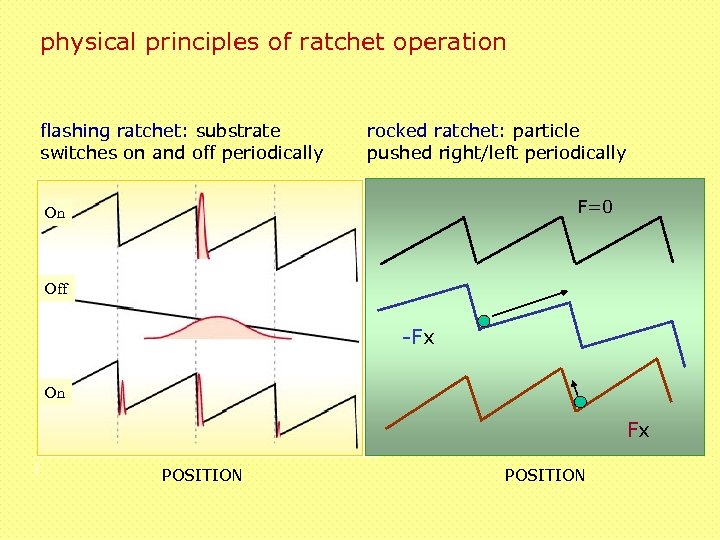physical principles of ratchet operation flashing ratchet: substrate switches on and off periodically rocked ratchet: particle pushed right/left periodically F=0 On Off -Fx On Fx POSITION

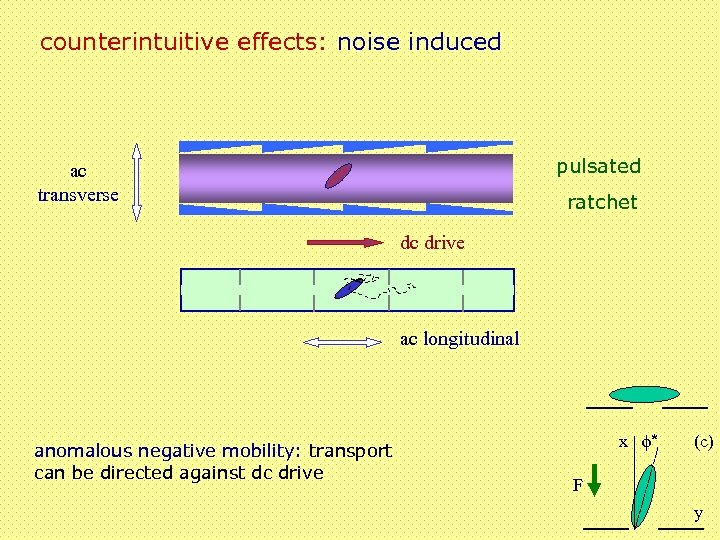counterintuitive effects: noise induced pulsated ac transverse ratchet dc drive ac longitudinal anomalous negative mobility: transport can be directed against dc drive x f* (c) F y

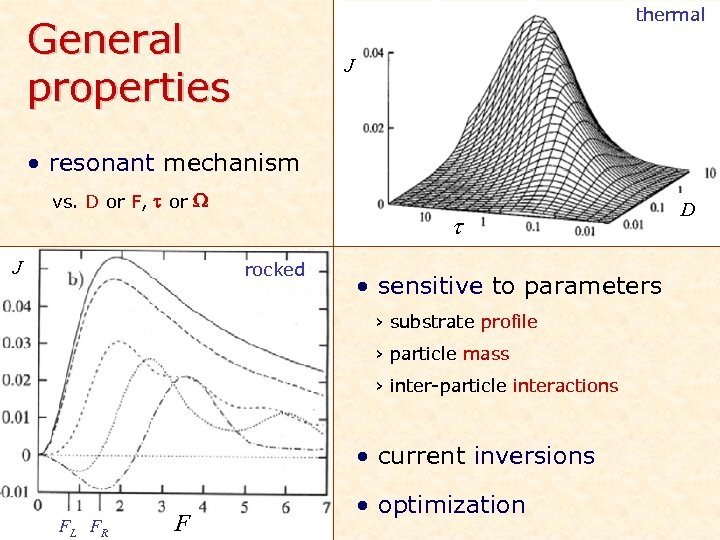thermal General properties J • resonant mechanism vs. D or F, t or W J t rocked • sensitive to parameters › substrate profile › particle mass › inter-particle interactions • current inversions FL FR F • optimization D

Applications biology inspired nano-devices - Rev Mod Phys 81, 387 (2009) Optical tweezers D. G. Grier et al, Appl. Phys. Lett. , 82, 3985 (2003). Artificial m-pores Z. Siwy and A. Fulinski, Phys. Rev. Lett. 89, 198103 (2002). Cold atoms traps F Renzoni et al, Phys. Rev. Lett. 95, 073003 (2005).

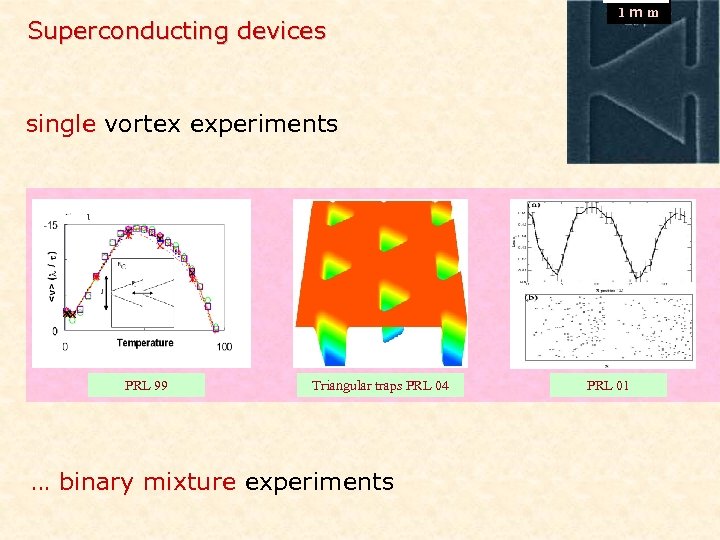Superconducting devices 1 mm single vortex experiments PRL 99 Triangular traps PRL 04 … binary mixture experiments PRL 01

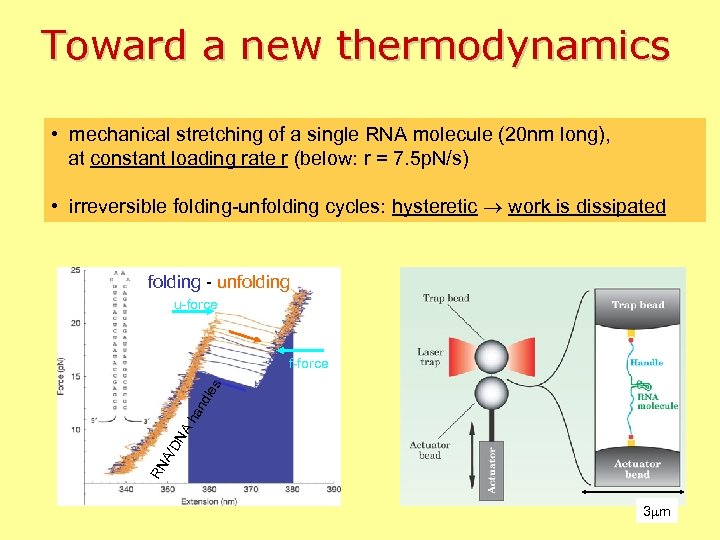Toward a new thermodynamics • mechanical stretching of a single RNA molecule (20 nm long), at constant loading rate r (below: r = 7. 5 p. N/s) • irreversible folding-unfolding cycles: hysteretic work is dissipated folding - unfolding u-force RN A/ DN A ha nd le s f-force 3 mm

Fluctuation theorems • n. e. forward process XF(t): XA XB ; T constant; XF(0) = XA initial equilibrium state; XF(t) = XB n. e. final state • n. e. reverse process XR(t): XB XA XR(0) = XB initial equilibrium state; XR(t)= XA n. e. final state • XR(t) is time reversed with respect to XF(t), i. e. XR(s) = XF(t-s) for 0 s t, with corresponding work p. d. PF(W) and PR(W) (Jarzynski, 1997) (Crooks, 1999)

Conclusions ¶ biology inspired nano-devices powered by noise ¶ role of noise at the small scales reconsidered ¶ noise harvesting to power nano-devices for ICT