The Ongoing Challenge — Tutorial The Illusion Of

The Ongoing Challenge - Tutorial The Illusion Of Capacity How do we determine what a FAB can produce in what time frame under what conditions? What Methods are available and used with what Frequency? How do they compare? part 5 of 4 Dr. Ken Fordyce & John Fournier, IBM Prof. John Milne, Clarkson University & Dr. Harpal Singh, CEO Arkieva ** Dr. Horst Zisgen, IBM, Rich Burda, Gary Sullivan (IBM, retired), Peter Lyon (IBM retired), Prof Chi-Tai Wang NCU (Taiwan) Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 1

Where we just visited & where we are going • Just Visited - How can we do a better job of representing FAB capacity within traditional central planning models. This topic is broken into two parts: – Part 1 - describing the core challenge, simply describing the current process and the basic nature of the question. – Part 2 – indentifying options to actually improve the representation of FAB capacity within central planning • Example link EPOS with PROFIT • “clearing function” that modifies capacity available or cycle time • Heuristic estimate of resource entity • Going to Visit - If we narrow our focus to just FAB planning and open to methods other than the traditional balance equations, what methods are available and how do they compare? Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 2

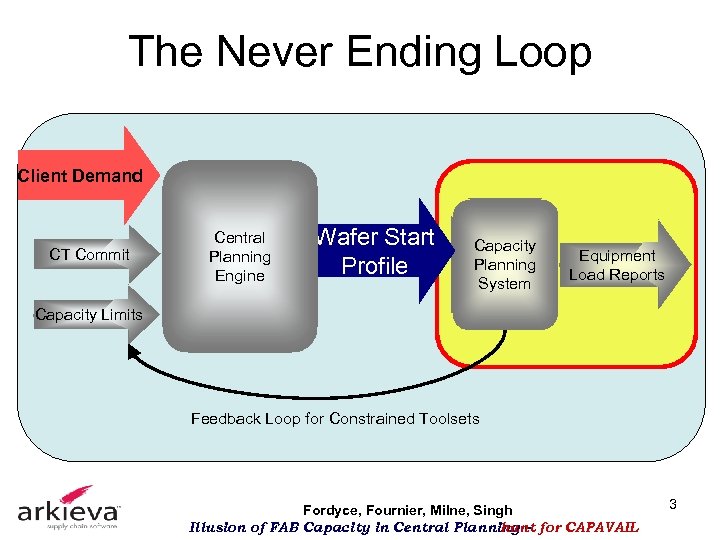The Never Ending Loop Client Demand CT Commit Central Planning Engine Wafer Start Profile Capacity Planning System Equipment Load Reports Capacity Limits Feedback Loop for Constrained Toolsets Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 3

Typical FAB Questions • Which lots are going to exit the FAB next week? • What is the near-term and long-term capability of a toolset (or fab)? • What is the expected incoming WIP at a toolset? • Will toolset operational outs rise or fall in the near future? • What will be the effect of adding/removing a certain tool from production? • What is the impact of expedites on cycletime? • Is the toolset’s current deployment adequate for incoming WIP? • Where should resources be deployed today? • Is there a window of opportunity for equipment work? Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 4

Typical FAB Questions • What tool sets are “broken” (insufficient capacity for projected load), what are the options to fix broken tool sets, and what is the impact of these actions? • Are the wafer start limits accurate? • Is the cycle time commit accurate? • When are the lots in the line exiting? • When would a projected set of wafer starts exit? Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 5

Emerging FAB Question • What is the impact of complex process time windows – Capacity required – Cycle time impact – Near term lot completion estimates • Different than “best practices” for schedule dispatch (not more important, just different) Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 6

Short List of “methods” to answer questions typically either start driven (forward) or demand driven (backward) • • • • • Research Compare, contrast Classify best use Examples WIPSIM vs EPOS vs Transport Equations Algebraic methods to allocate steady state workload to tool sets Extending the algebraic method to handle deployment or cascade (essentially CAPS) “race” track with / without limits (as wafers) WIP Projector type logic working sectors, cycle times, and aggregate capacity Daily output planning SLIM Rule Based simulation Time Slide (TALC) Queuing models and static capacity planning queuing networks / fluid models (EPOS) discrete event simulation (WIPSIM) Clearing Functions Column generation optimization type simulation Combination of simulation and optimization Clearing “function” incorporated into optimization Transport equations via partial differential equations New text Production Planning and Control for Semiconductor Wafer Fabrication Facilities Monch, Fowler, et al Springer Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 9

Clearing Functions within LP • Armbruster & Uzsoy 2012, “Continuous Dynamic Models, Clearing Functions, and Discrete-Event Simulation in Aggregate Production Planning”, Production Planning Tutorials in Operations Research”, isbn 978 -0 -9843378 -3 -5, dx. doi. org/10. 1287/educ. 1120. 0102 – ACF: allocated Clearing Function pp. 10 -13 • Asmundsson et al, “Production planning models with resources subject to congestion, ” Naval Res. Logistics, vol. 56, no. 2, pp. 142– 157, Mar. 2009. • Asmundsson et al, “Tractable nonlinear production planning models for semiconductor wafer fabrication facilities, ” IEEE Trans. Semicond. Manuf. , vol. 19, no. 1, pp. 95– 111, 2006 Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 10

Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 11

Sources • • Tibbits, B, 1993, “Flexible simulation of a complex semiconductor manufacturing line using a rule-based”, IBM R&D Journal Sullivan, G, 1992, “Daily Output Planning”, Expert Systems with Applications Sullivan, G, 1995, “Dynamically Generated Rapid Response Capacity Planning Model” Bermon, S. , and S. Hood. 1999. Capacity optimization planning system (CAPS). Interfaces 29 (5): 31– 50. Bagchi, S et al 2008. A Full-factory Simulator As A Daily Decision-support Tool For 300 mm Wafer Fabrication Productivity, MASM 2008 Zisgen, H. et al 2008. A Queueing Network Based System To Model Capacity And Cycle Time For Semiconductor Fabrication, MASM 2008 Schelasin, R 2011. Using Static Capacity Modeling And Queuing Theory Equations To Predict Factory Cycle Time Performance In Semiconductor Manufacturing, MASM 2011 Levy, J. et al 2010, ”Method For Determining Amount of Product Released Into a Time Sensitive Operation”, MASM 2010 Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 12

Sources • • • Armbruster & Uzsoy 2012, “Continuous Dynamic Models, Clearing Functions, and Discrete-Event Simulation in Aggregate Production Planning”, Production Planning Tutorials in Operations Research”, isbn 978 -0 -9843378 -3 -5, dx. doi. org/10. 1287/educ. 1120. 0102 Kacar, Irdeem, & Uzsoy, 2011, “An Experimental Comparison of Production Planning Using Clearing Functions and Iterative Linear Programming-Simulation Algorithms”, IEEE Transactions on Semiconductor MFG, Irdeem, Kacar, & Uzsoy, 2010, An Exploratory Analysis of Two Iterative Linear Programming—Simulation Approaches for Production Planning, Ieee Transactions On Semiconductor Manufacturing, Vol. 23, No. 3, August 2010 Asmundsson et al, “Production planning models with resources subject to congestion, ” Naval Res. Logistics, vol. 56, no. 2, pp. 142– 157, Mar. 2009. Asmundsson et al, “Tractable nonlinear production planning models for semiconductor wafer fabrication facilities, ” IEEE Trans. Semicond. Manuf. , vol. 19, no. 1, pp. 95– 111, 2006 H. Missbauer. Models of the transient behaviour of production units to optimize the aggregate material flow. International Journal of Production Economics 118(2): 387{397, 2002. H. Missbauer and R. Uzsoy. Optimization models for production planning. K. Kempf, P. Keskinocak, and R. Uzsoy, eds. Planning Production and Inventories in the Extended Enterprise: A State of the Art Handbook. Springer Verlag, New York, 437{508, A 47 2011. [ Modigliani and F. E. Hohn. Production planning over time and the nature of the expectation Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 13

Presentations at MASM 2012 • Using Iterative Simulation to Incorporate Load-Dependent Lead Times in Master Planning Heuristics; Lars Moench and Thomas Ponsignon (Infineon). Abstract: In this paper, we consider heuristics for master planning in semiconductor manufacturing. While lead times are typically assumed as fixed in production planning, we use iterative simulation to take load-dependent lead times into account. An Auto. Sched AP simulation model of a semiconductor supply chain is used for implementing the scheme. Simulation results show that the iterative scheme converges fast and leads to less variable, more profitable production plans compared to planes obtained by the fixed lead time approach. • Product Mix Optimization for a Semiconductor Fab: Modeling Approaches and Decomposition Techniques; Andreas Klemmt, Martin Romauch, Walter Laure (Infineon Technologies). Abstract: For optimizing a semiconductor fab we are aiming to match the production capabilities, capacities and the demand in the most profitable way. In this paper we address a linear model of the product mix problem considering product dependent demand limits (obligations and demand forecast) and profits while respecting the capacity bounds of the production facility. Since the capacity consumption is highly depended on choosing from different production alternatives we are implicitly solving a static capacity planning problem for each product mix. This kind of planning approach is supported by the fluid flow concept of complete resource pooling in high traffic. We propose a general model that considers a wide range of objectives and we introduce a heuristic based on a decomposition of the static capacity planning problem. The computational study of the approaches is based on real world data and on randomly generated instances. Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 14

Presentations at MASM 2012 • An Evaluation of an Option Contract in Semiconductor Supply Chains Konstanze Knoblich (Infineon Technologies) and Cathal Heavey and Peter Williams (University of Limerick), Abstract: The purpose of this paper is to evaluate an option contract within a semiconductor supply chain consisting of one semiconductor manufacturer and one customer. In an option contract the customer pays an upfront fee (option price) for an option to purchase product. A simulation model is used to compare the performance of an option contract against a standard supply contract used in a semiconductor supply chain in terms of delivery performance and costs for the supply chain partners Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 15

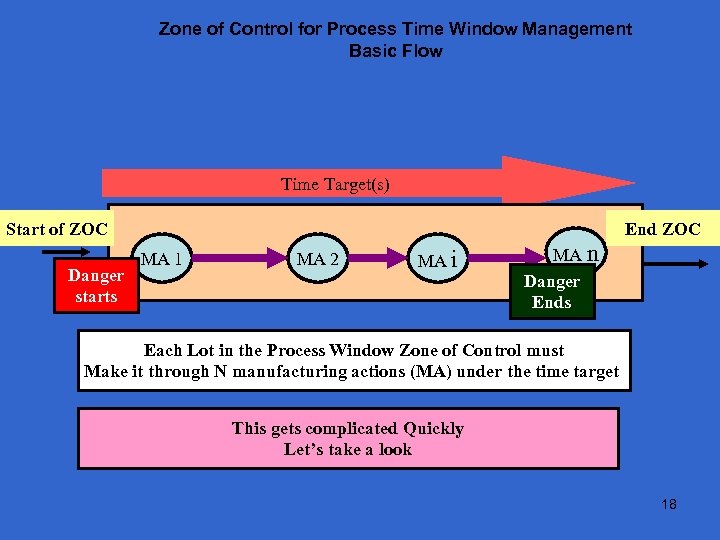Zone of Control for Process Time Window Management Basic Flow Time Target(s) Start of ZOC Danger starts End ZOC MA 1 MA 2 MA i MA n Danger Ends Each Lot in the Process Window Zone of Control must Make it through N manufacturing actions (MA) under the time target This gets complicated Quickly Let’s take a look 18

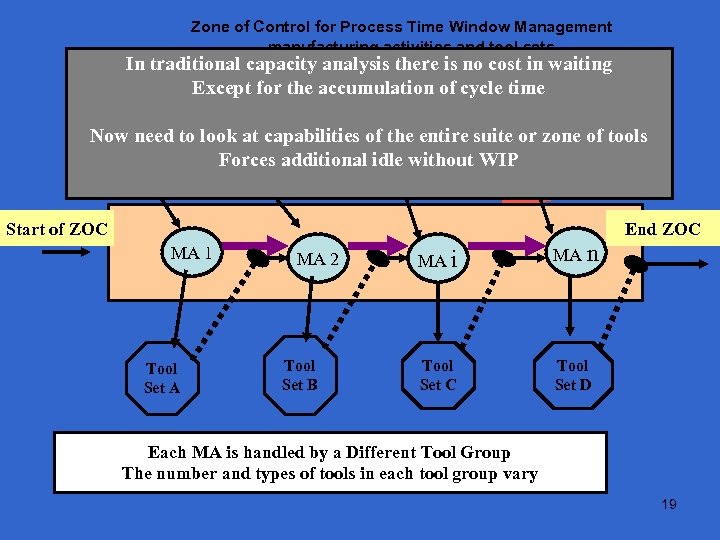Zone of Control for Process Time Window Management - manufacturing activities and tool sets In traditional capacity analysis there is no cost in waiting Except for the accumulation of cycle time Now need to look at capabilities of the entire suite or zone of tools Forces additional idle without WIP Time Target(s) Start of ZOC End ZOC MA 1 Tool Set A MA 2 Tool Set B MA i MA n Tool Set C Tool Set D Each MA is handled by a Different Tool Group The number and types of tools in each tool group vary 19

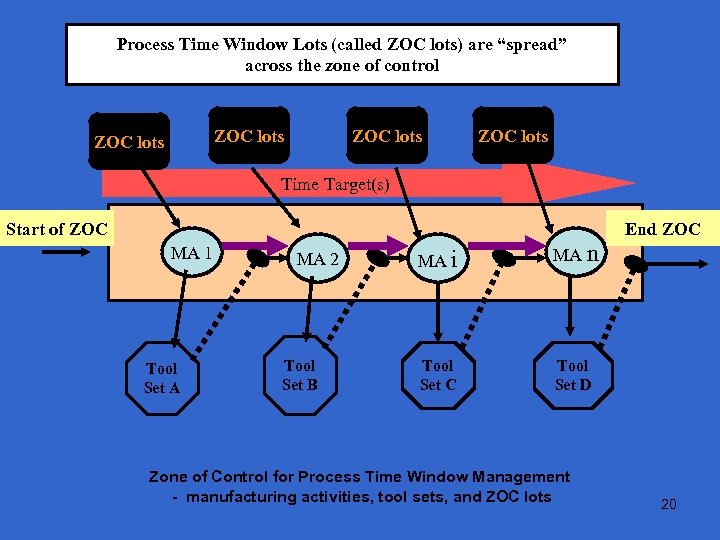Process Time Window Lots (called ZOC lots) are “spread” across the zone of control ZOC lots Time Target(s) Start of ZOC End ZOC MA 1 Tool Set A MA 2 Tool Set B MA i MA n Tool Set C Tool Set D Zone of Control for Process Time Window Management - manufacturing activities, tool sets, and ZOC lots 20

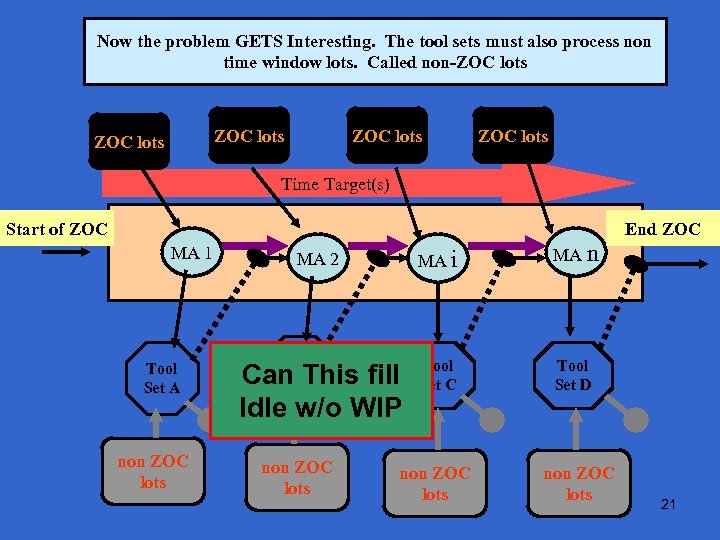Zone of Control for Process Time Window Management Now themanufacturing activities, tool The tool sets must also process non - problem GETS Interesting. sets, ZOC lots, non ZOC lots time window lots. Called non-ZOC lots ZOC lots Time Target(s) Start of ZOC End ZOC MA 1 Tool Set A non ZOC lots MA 2 MA i MA n Tool Can This fill Set B Idle w/o WIP Tool Set C Tool Set D non ZOC lots 21

Core of Algebraic Method • Algebra methods – the FAB plans to start three products (A, B, and C) at the rate of 10, 30, and 20 wafer starts per day. Product A requires 3 passes at photo, Product B required 4 passes, and C requires 2 passes. With some simple arithmetic I can determine the work load on the photo tools in terms of passes. Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 28

Basics of FAB Planning Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 29

Basics of FAB Planning • Focus on matching assets with demand • Three major classes – Aggregate FAB planning – Deployment or near term tool planning – WIP Projection • Forward flow of starts dominate method as opposed to pulling to meet demand • Wide variation in methods • Wide variation in how much FAB complexity of deployment and operating curve is handled Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 30

Basics of Algebraic Approach to Aggregate FAB Planning Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 31

Basics of Aggregate Factory Planning • focused on assessing the ability of the factory to meet certain demand looking to identify “broken” toolsets and creating the capacity inputs required by central planning. • Demand is stated as a starts profile and a lead (cycle) time commit for each part. • Various levels of sophistication in handling operating curve, deployment, mix variability, etc • The key challenges for the factory planner are: – Determine if the workload can be allocated across the tools in such a way that all of the workload can be allocate without violating capacity constraints – If insufficient capacity exits • find the optimal mix of workload that can be met without violating capacity constraints • find the optimal allocation that either minimizes additional capacity needed incorporating some type of fair share of pain Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 32

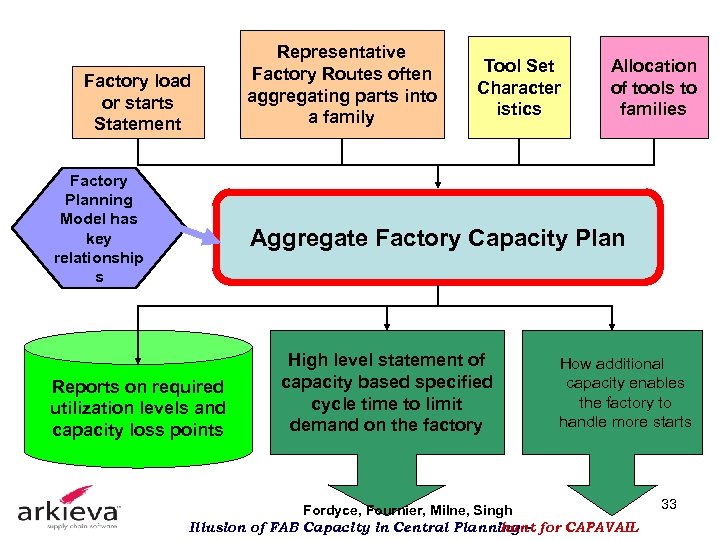Factory load or starts Statement Factory Planning Model has key relationship s Representative Factory Routes often aggregating parts into a family Tool Set Character istics Allocation of tools to families Aggregate Factory Capacity Plan Reports on required utilization levels and capacity loss points High level statement of capacity based specified cycle time to limit demand on the factory How additional capacity enables the factory to handle more starts Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 33

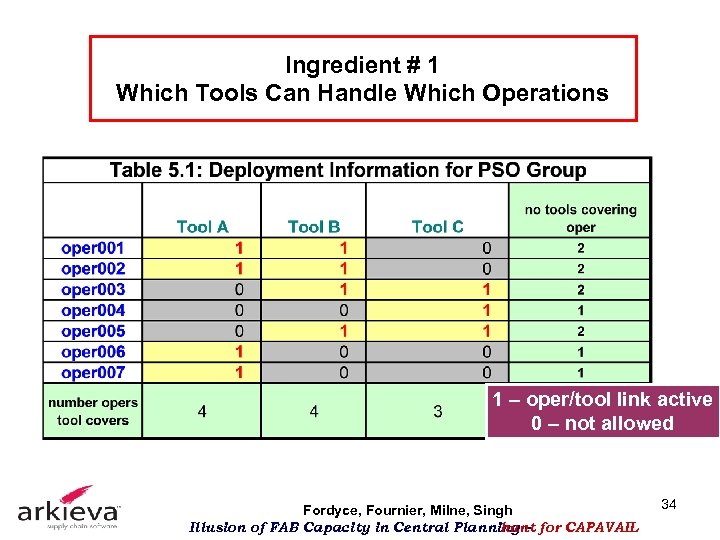Ingredient # 1 Which Tools Can Handle Which Operations 1 – oper/tool link active 0 – not allowed Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 34

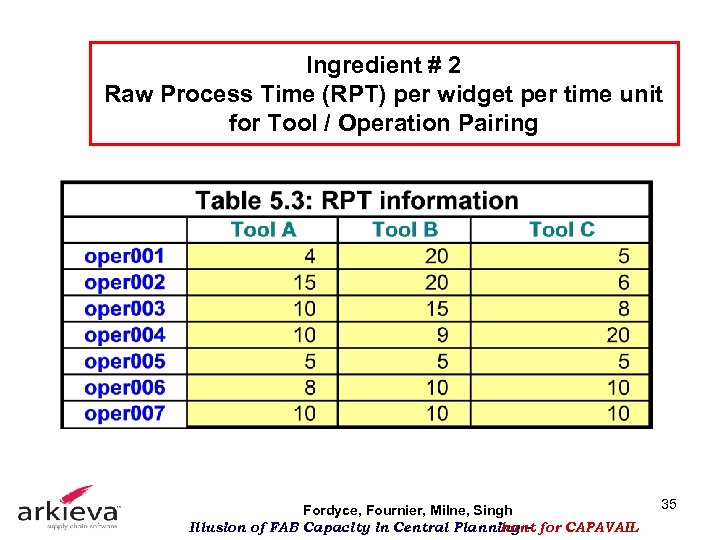Ingredient # 2 Raw Process Time (RPT) per widget per time unit for Tool / Operation Pairing Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 35

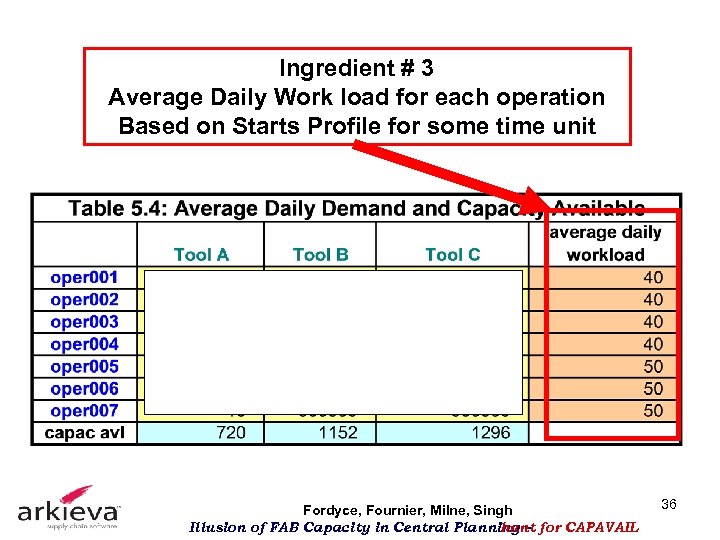Ingredient # 3 Average Daily Work load for each operation Based on Starts Profile for some time unit Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 36

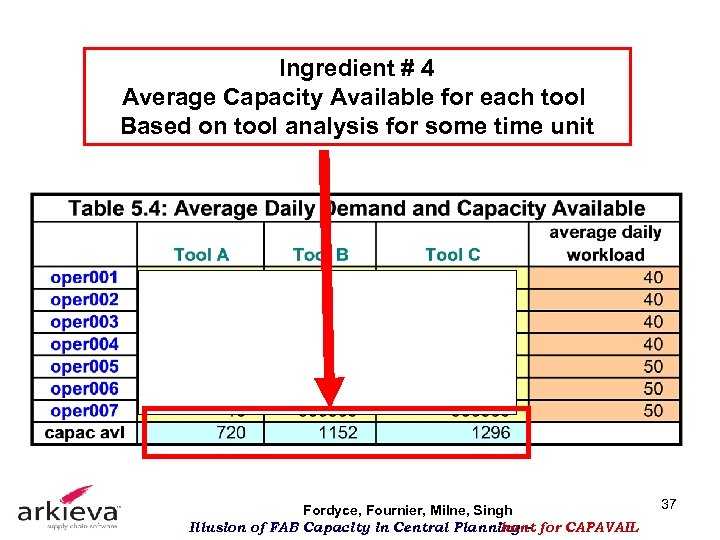Ingredient # 4 Average Capacity Available for each tool Based on tool analysis for some time unit Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 37

Ingredient # 5 “cycle time tax” to reduce capacity available to effective capacity available To account for required idle without WIP Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 38

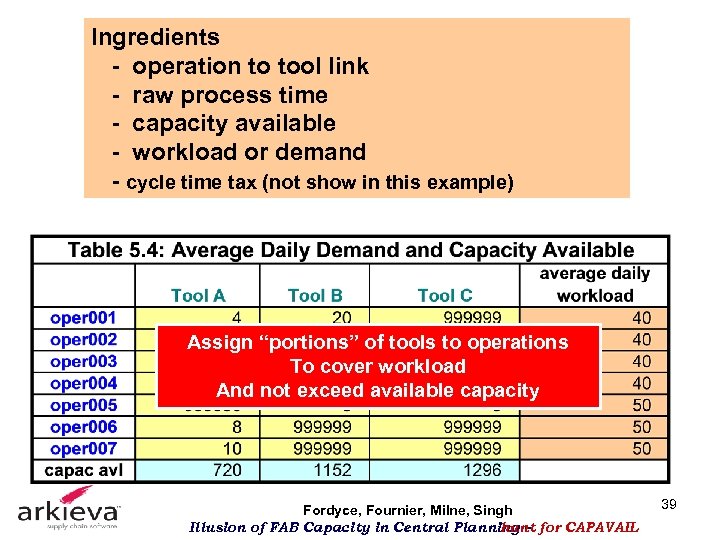Ingredients - operation to tool link - raw process time - capacity available - workload or demand - cycle time tax (not show in this example) Assign “portions” of tools to operations To cover workload And not exceed available capacity Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 39

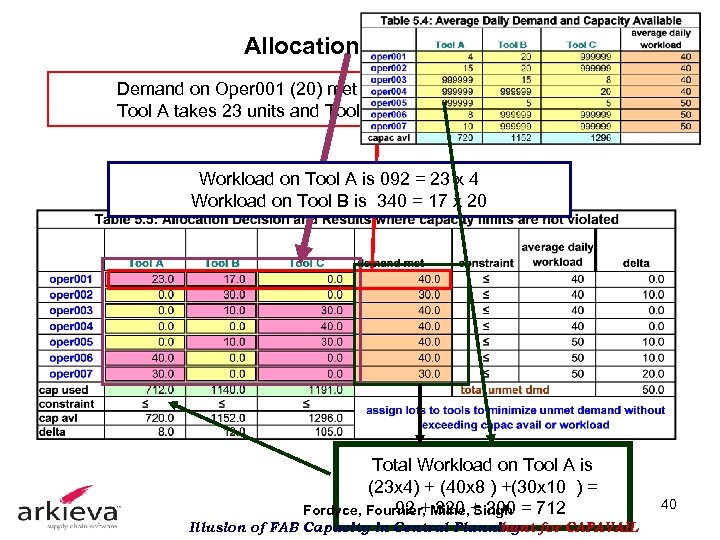Allocation Decision # 1 Demand on Oper 001 (20) met as follows Tool A takes 23 units and Tool B gets 17 Workload on Tool A is 092 = 23 x 4 Workload on Tool B is 340 = 17 x 20 Total Workload on Tool A is (23 x 4) + (40 x 8 ) +(30 x 10 ) = 92 + 320 Singh Fordyce, Fournier, Milne, + 300 = 712 Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 40

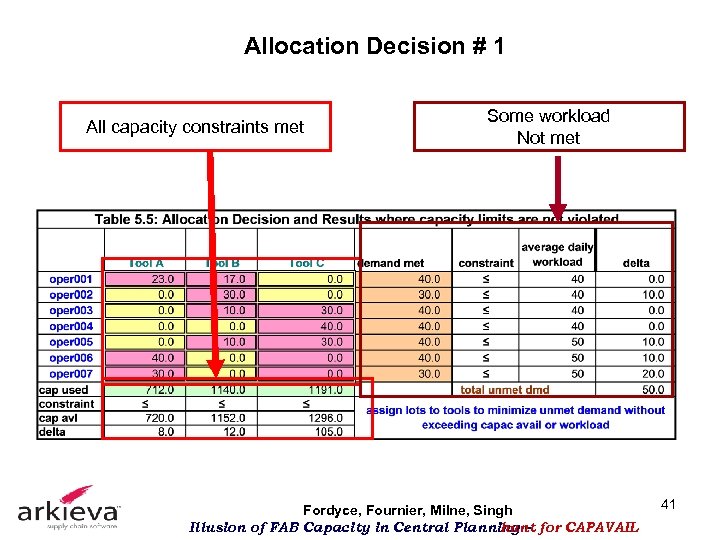Allocation Decision # 1 All capacity constraints met Some workload Not met Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 41

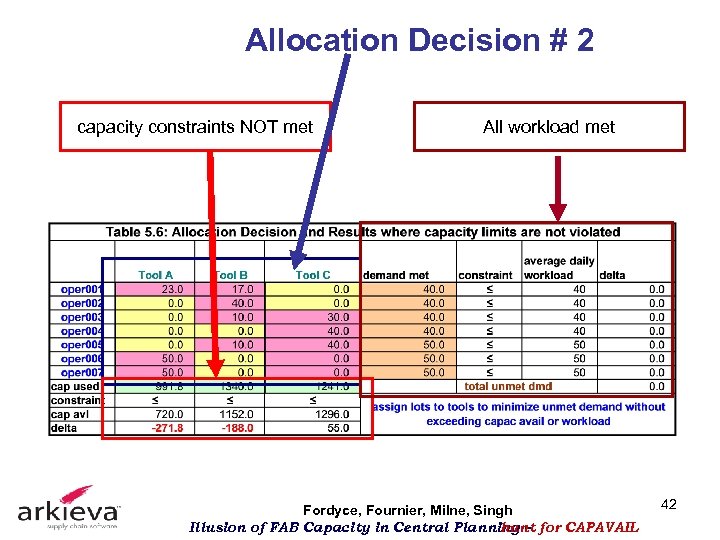Allocation Decision # 2 capacity constraints NOT met All workload met Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 42

Clearing Functions within LP • Armbruster & Uzsoy 2012, “Continuous Dynamic Models, Clearing Functions, and Discrete-Event Simulation in Aggregate Production Planning”, Production Planning Tutorials in Operations Research”, isbn 978 -0 -9843378 -3 -5, dx. doi. org/10. 1287/educ. 1120. 0102 – ACF: allocated Clearing Function pp. 10 -13 • Asmundsson et al, “Production planning models with resources subject to congestion, ” Naval Res. Logistics, vol. 56, no. 2, pp. 142– 157, Mar. 2009. • Asmundsson et al, “Tractable nonlinear production planning models for semiconductor wafer fabrication facilities, ” IEEE Trans. Semicond. Manuf. , vol. 19, no. 1, pp. 95– 111, 2006 Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 43

Sources • • Tibbits, B, 1993, “Flexible simulation of a complex semiconductor manufacturing line using a rule-based”, IBM R&D Journal Sullivan, G, 1992, “Daily Output Planning”, Expert Systems with Applications Sullivan, G, 1995, “Dynamically Generated Rapid Response Capacity Planning Model” Bermon, S. , and S. Hood. 1999. Capacity optimization planning system (CAPS). Interfaces 29 (5): 31– 50. Bagchi, S et al 2008. A Full-factory Simulator As A Daily Decision-support Tool For 300 mm Wafer Fabrication Productivity, MASM 2008 Zisgen, H. et al 2008. A Queueing Network Based System To Model Capacity And Cycle Time For Semiconductor Fabrication, MASM 2008 Schelasin, R 2011. Using Static Capacity Modeling And Queuing Theory Equations To Predict Factory Cycle Time Performance In Semiconductor Manufacturing, MASM 2011 Levy, J. et al 2010, ”Method For Determining Amount of Product Released Into a Time Sensitive Operation”, MASM 2010 Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 44

Sources • • • Armbruster & Uzsoy 2012, “Continuous Dynamic Models, Clearing Functions, and Discrete-Event Simulation in Aggregate Production Planning”, Production Planning Tutorials in Operations Research”, isbn 978 -0 -9843378 -3 -5, dx. doi. org/10. 1287/educ. 1120. 0102 Kacar, Irdeem, & Uzsoy, 2011, “An Experimental Comparison of Production Planning Using Clearing Functions and Iterative Linear Programming-Simulation Algorithms”, IEEE Transactions on Semiconductor MFG, Irdeem, Kacar, & Uzsoy, 2010, An Exploratory Analysis of Two Iterative Linear Programming— Simulation Approaches for Production Planning, Ieee Transactions On Semiconductor Manufacturing, Vol. 23, No. 3, August 2010 Asmundsson et al, “Production planning models with resources subject to congestion, ” Naval Res. Logistics, vol. 56, no. 2, pp. 142– 157, Mar. 2009. Asmundsson et al, “Tractable nonlinear production planning models for semiconductor wafer fabrication facilities, ” IEEE Trans. Semicond. Manuf. , vol. 19, no. 1, pp. 95– 111, 2006 H. Missbauer. Models of the transient behaviour of production units to optimize the aggregate material flow. International Journal of Production Economics 118(2): 387{397, 2002. H. Missbauer and R. Uzsoy. Optimization models for production planning. K. Kempf, P. Keskinocak, and R. Uzsoy, eds. Planning Production and Inventories in the Extended Enterprise: A State of the Art Handbook. Springer Verlag, New York, 437{508, A 47 2011. [60] F. Modigliani and F. E. Hohn. Production planning over time and the nature of the expectation Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 45

Presentations at MASM 2012 • Using Iterative Simulation to Incorporate Load-Dependent Lead Times in Master Planning Heuristics; Lars Moench and Thomas Ponsignon (Infineon). Abstract: In this paper, we consider heuristics for master planning in semiconductor manufacturing. While lead times are typically assumed as fixed in production planning, we use iterative simulation to take load-dependent lead times into account. An Auto. Sched AP simulation model of a semiconductor supply chain is used for implementing the scheme. Simulation results show that the iterative scheme converges fast and leads to less variable, more profitable production plans compared to planes obtained by the fixed lead time approach. • Product Mix Optimization for a Semiconductor Fab: Modeling Approaches and Decomposition Techniques; Andreas Klemmt, Martin Romauch, Walter Laure (Infineon Technologies). Abstract: For optimizing a semiconductor fab we are aiming to match the production capabilities, capacities and the demand in the most profitable way. In this paper we address a linear model of the product mix problem considering product dependent demand limits (obligations and demand forecast) and profits while respecting the capacity bounds of the production facility. Since the capacity consumption is highly depended on choosing from different production alternatives we are implicitly solving a static capacity planning problem for each product mix. This kind of planning approach is supported by the fluid flow concept of complete resource pooling in high traffic. We propose a general model that considers a wide range of objectives and we introduce a heuristic based on a decomposition of the static capacity planning problem. The computational study of the approaches is based on real world data and on randomly generated instances. Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 46

Presentations at MASM 2012 • An Evaluation of an Option Contract in Semiconductor Supply Chains Konstanze Knoblich (Infineon Technologies) and Cathal Heavey and Peter Williams (University of Limerick), Abstract: The purpose of this paper is to evaluate an option contract within a semiconductor supply chain consisting of one semiconductor manufacturer and one customer. In an option contract the customer pays an upfront fee (option price) for an option to purchase product. A simulation model is used to compare the performance of an option contract against a standard supply contract used in a semiconductor supply chain in terms of delivery performance and costs for the supply chain partners Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 47

Fordyce, Fournier, Milne, Singh Illusion of FAB Capacity in Central Planning – for CAPAVAIL hunt 48