THE MICROCALORIMETER AS POWER STANDARD Contents 1

THE MICROCALORIMETER AS POWER STANDARD

Contents 1. Dry-load broadband microcalorimeter 2. Simplified microcalorimeter models 3. Measurements with the Microcalorimeter: data computation and results correction 4. Accelerated against long-term microcalorimeter measurement strategies

Introduction The microcalorimeter is a measurement system considered as primary power standard. Basically, it is used for the effective efficiency measurements of the bolometer power sensors, like thermistor or barretter mounts, in order to obtain transfer standards. The last microcalorimetric techniques improvements, both hardware and software, make from thermocouple power sensors a good alternative to the bolometric power sensors.

Design Leading Concepts The system has been designed according to the following lines: Twin thermal load structure Dry thermostatization instead of liquid use for this Maximum possible computer control Working with bolometer and thermocouple power sensors

System Description The microcalorimeter (INRi. M) may be classified as a dry type adiabatic calorimeter. Its thermal load consists of: the sensor under test (SUT), a thermally equivalent device (dummy sensor TDL) and a thermopile that senses the temperature difference between SUT and TDL. The core thermostatization is obtained by means of multiple Alshields, separated by polystyrene foam (or air). An intermediate shield is actively controlled by Peltier junctions, while the other two work only as passive thermal filter. Measured thermal stability on the inner shield is below 5 m. K.

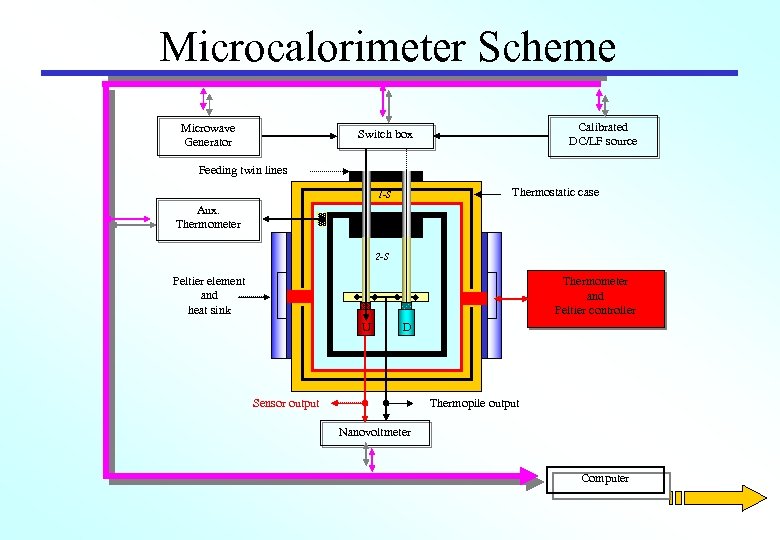Microcalorimeter Scheme Microwave Generator Calibrated DC/LF source Switch box Feeding twin lines Thermostatic case 1 -S Aux. Thermometer 2 -S Peltier element and heat sink Thermometer and Peltier controller U D Sensor output Thermopile output Nanovoltmeter Computer

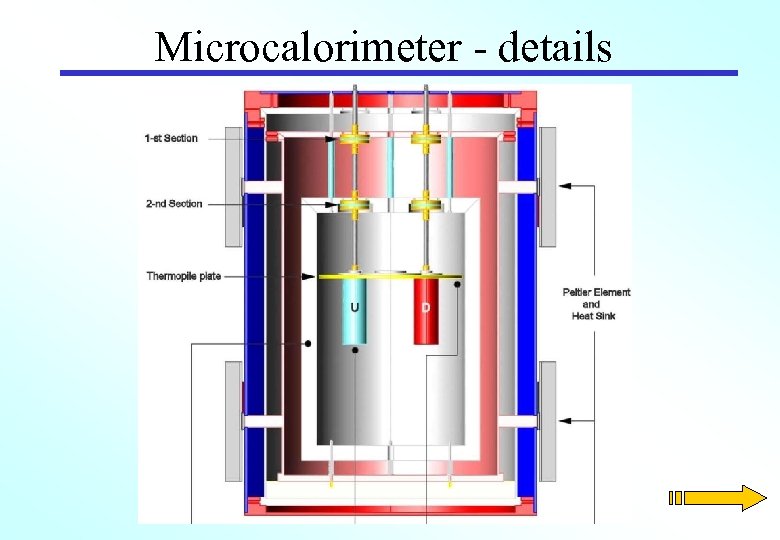Microcalorimeter - details

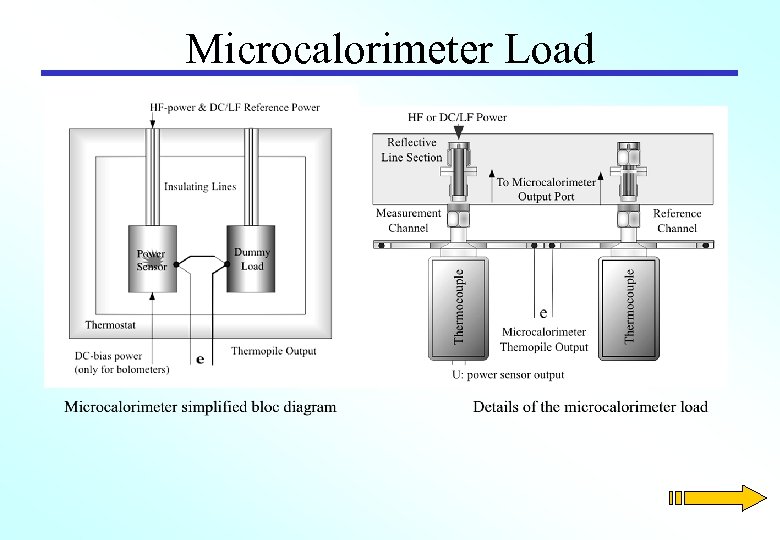Microcalorimeter Load

Insulation Lines The feeding lines are made of two parts of coaxial line having a low thermal conductance. These sectors have a common thermal ground on the third shield, but they are not symmetric. In the sector S-1 only the inner conductor is a thermal insulator. The sector S-2 has thin wall conductors. This structure allows a better rejection of thermal noise.

Microcalorimeter Thermopile The thermopile pair consists of two independent series of Cu. Constantan thermojunctions, radially distributed around of the output connectors. The temperature difference is linearly proportional to the measured effective efficiency . By combining the signals from the two series, the temperature difference between SUT and TDL is obtained.

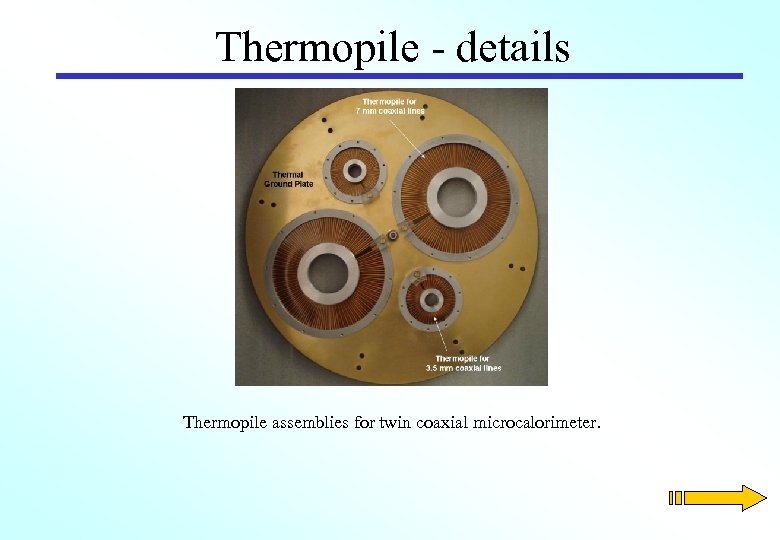Thermopile - details Thermopile assemblies for twin coaxial microcalorimeter.

System Theory The effective efficiency e is determined by temperature variation of the sensor mount when it is alternatively supplied with high frequency (HF) power and reference (REF) power. The thermopile output e follows an increasing or decreasing exponential trend, toward finite asymptotes e 1, e 2. To take into account the heat distribution, e must be resolved into at least two components one related to power sensor and the other to feeding line: - is the Seebek coefficient of thermopile junctions; - R, a constant depending on thermodynamic parameters - k 1 , k 2, describe the power separation between SUT and feeding line - PS , PIL, the power dissipated in the sensor and in the insulating line respectively.

System Theory Effective efficiency is obtained by applying thermoelectric equation (1) after each power substitution (HF REF) at thermodynamic equilibrium. e. R=e 2/e 1 - asymptotic thermopile output ratio k=k 2 /k 1 - power separation constant ratio g - microcalorimeter calibration factor The microcalorimeter has two working modes: Measurement: e. R measurement Calibration: g determination

Calibration Mode In the calibration mode the correction factor g is determined through: a - feeding line attenuation measurements (a. HF , a. REF). b - k ratio measurement (k=k 2/k 1). Step a requires VNA measurements only: Step b requires a special microcalorimeter configuration: 1. Supplying hot sensor with REF-power, thermopile output is e 2= Rk 1 PS |REF. 2. Then hot sensor is substituted by a short (open) circuit having same thermal capacity. Supplying it with equivalent HF-power, thermopile output is e 1 = Rk 2 PIL|HF. Under condition thermodynamic system is unchanged, it results: SC This equation is related to the long-term measurement algorithm. An equivalent expression exists for medium-term measurements.

Long-term Measurement Mode e. R is directly measured, if there is a waiting state of about 10 ( is the system time constant) before sampling thermopile output e at each power substitution (HF REF).

Mediu-term Measurement Mode e. R is obtained from the next equation, if the waiting state is < 10 : eτ is the ratio of the extreme values of thermopile output voltage, e. M, em; TSW - the switching time; H - a correction factor for the limited switching time:

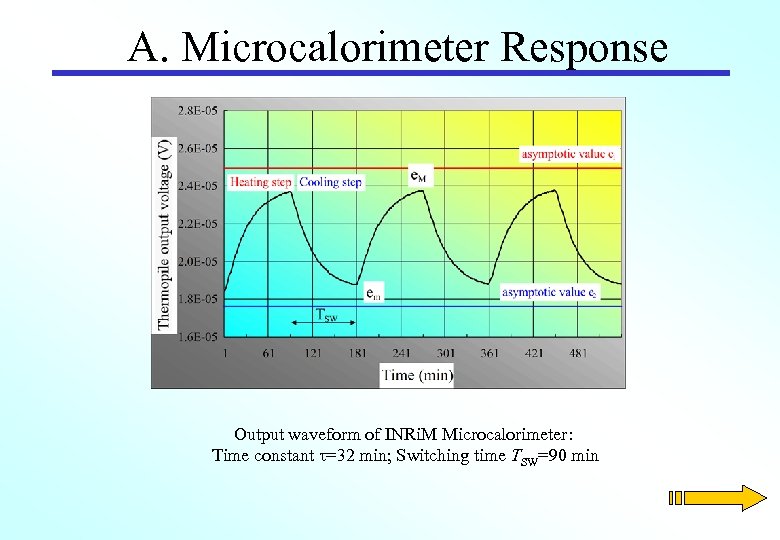A. Microcalorimeter Response Output waveform of INRi. M Microcalorimeter: Time constant =32 min; Switching time TSW=90 min

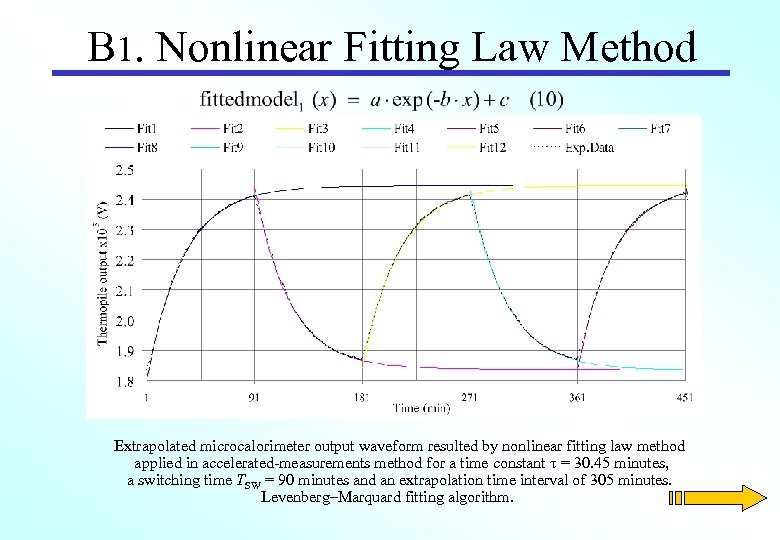B 1. Nonlinear Fitting Law Method Extrapolated microcalorimeter output waveform resulted by nonlinear fitting law method applied in accelerated-measurements method for a time constant = 30. 45 minutes, a switching time TSW = 90 minutes and an extrapolation time interval of 305 minutes. Levenberg–Marquard fitting algorithm.

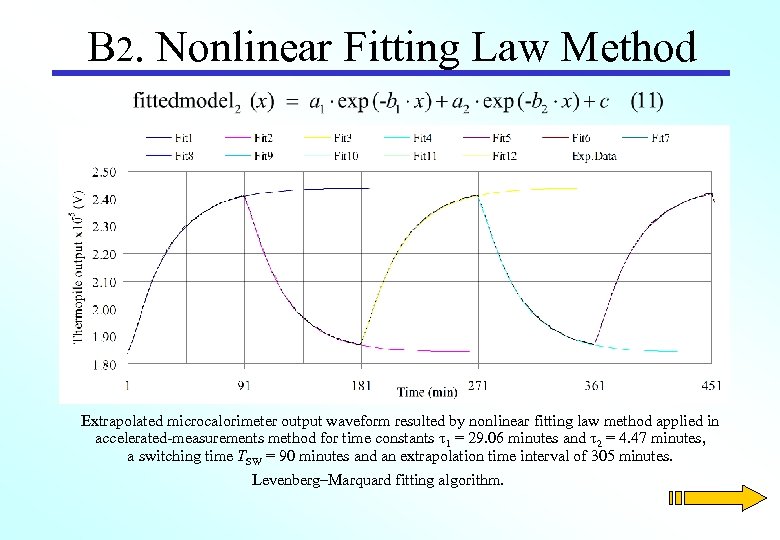B 2. Nonlinear Fitting Law Method Extrapolated microcalorimeter output waveform resulted by nonlinear fitting law method applied in accelerated-measurements method for time constants 1 = 29. 06 minutes and 2 = 4. 47 minutes, a switching time TSW = 90 minutes and an extrapolation time interval of 305 minutes. Levenberg–Marquard fitting algorithm.

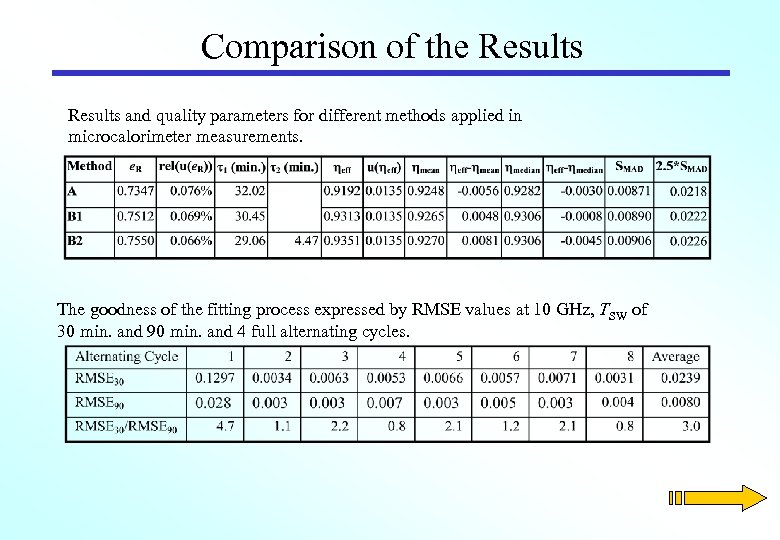Comparison of the Results and quality parameters for different methods applied in microcalorimeter measurements. The goodness of the fitting process expressed by RMSE values at 10 GHz, TSW of 30 min. and 90 min. and 4 full alternating cycles.

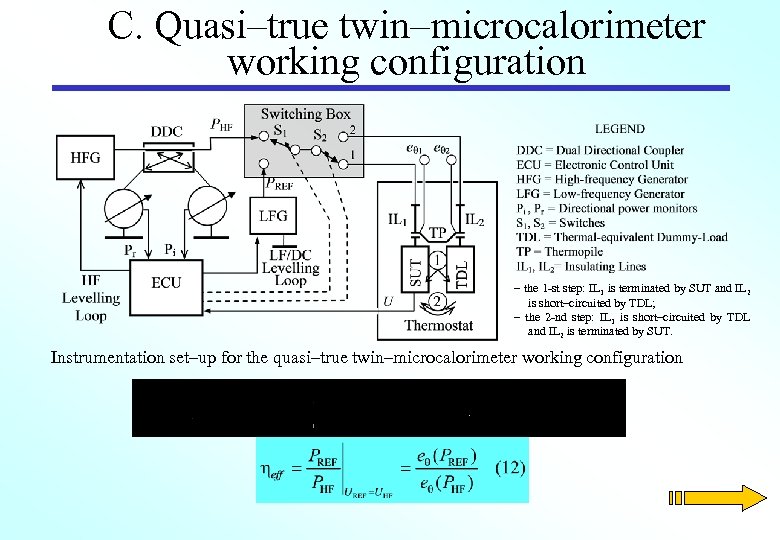C. Quasi–true twin–microcalorimeter working configuration – the 1 -st step: IL 1 is terminated by SUT and IL 2 is short–circuited by TDL; – the 2 -nd step: IL 1 is short–circuited by TDL and IL 2 is terminated by SUT. Instrumentation set–up for the quasi–true twin–microcalorimeter working configuration

D. Variable Time-interval Algorithm - the input power alternates as reference power on/off or test power on/off for the same output effect; - the microcalorimeter output is varying now all the time between the same two limits; - the up-time becomes now dependent on the test frequency through effective efficiency of the SUT - the feeding lines losses for the down-time remain almost constant; - microcalorimeter is working in a quite stationary regime and the test frequencies order is not important; - the measurements with the reference power must be repeated only few times; - the true-twin configuration can now really working; - the voltage of thermopile is now detected as; - the lower limits is not perturbated because it is performed in a quite-ideal required state.

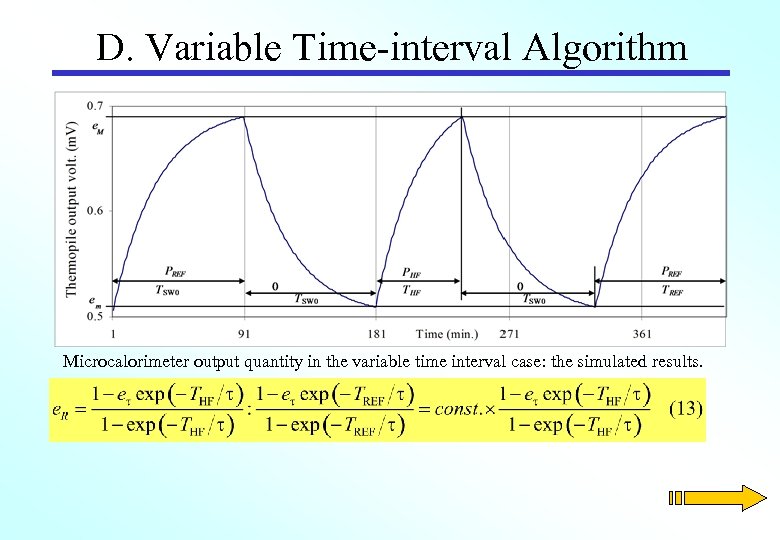D. Variable Time-interval Algorithm Microcalorimeter output quantity in the variable time interval case: the simulated results.

Conclusion • The microcalorimeter measurements can be performed by applying various strategies and algorithms. • The long-term measurement algorithm is time-consuming, but it remains the reference one for the other developed accelerated algorithms. • The usefulness of the fitting method can not be proved by uncertainty improvement, but the changes in the wanted quantity can modify the result even in a key comparison. • In this kind of experiments, the measurement time is never enough long and a good correction can be done by a suitable curve fitting method. • An adaptive automated measurement system can controls the switching time in a such manner which will lead to an adequate uncertainty. • The manly part of the uncertainty is from microcalorimeter calibration step and the accelerated measurements can appear as not enough accurately. • The new proposed accelerated algorithms assure ideal equations for computing of the wanted quantity, the effective efficiency of the investigated power sensor.

References [1] Fantom A. E. , Radiofrequency & microwave power measurement, Peter Peregrinus Ltd. , London, 1990. [2] Ascroft J. , “Developments in Coaxial Power Standards at NPL”, IEEE Transaction on Instrumentation and Measurement, vol. 48, no. 2, pp 647 – 649, 1999. [3] Clauge F. R. , "A Method to Determine the Calorimetric Equivalence Correction for a Coaxial Microwave Microcalorimeter", IEEE Transaction on Instrum. Meas. , 43, 3, pp. 421 -425 (1994). [4] Brunetti L. , Vremera E. , “A new microcalorimeter for measurements in 3. 5 -mm coaxial line”, IEEE Transaction on Instrumentation and Measurement, vol. 52, no. 2, pp. 320 - 323, 2003. [5] Brunetti L. , Vremera E. , “New calibration method for microcalorimeters”, IEEE Transaction on Instrumentation and Measurement, vol. 54, no. 2, pp. 684 -687, 2005. [6] Mellouet B. , et al. "Fast Method Applied to the Measurement of Microwave Power Standards", IEEE Transaction on Instrum. Meas. , vol. 50, 2, pp. 381 -384 (2001). [7] Rietto G. , “Long-term Efficiency Measurements on Bolometer Mounts”, IEEE Transaction on Instrumentation and Measurement, vol. IM-23, no. 4, pp 420 – 422, 1974. [8] Yoshinobu Okano and Takeumi Inoue, “Automatic Microcalorimeter System for Broadband Power Measurement in 75 GHz – 110 GHz Range”, IEEE Trans. on Instrum. and Measurement, vol. 50, no. 2, pp 385 – 388, 2001. [9] Meijer G. C. M. and Herwaarden A. W. (Editors), Thermal Sensors, Institute of Physics Publishing, Bristol, 1994. [10] Vremera E. et al. , “Alternative Procedures in Realizing of the High Frequency Power Standards with Microcalorimeter and Thermoelectric Power Sensors”, 10. 1016/j. measurement. 2008. 06. 010, in press. [11] * * * EA – 4/02: Expression of the Uncertainty of Measurement in Calibration, 1999.