Скачать презентацию The Metric System Meters Grams and Liters Скачать презентацию The Metric System Meters Grams and Liters

5bff8184204c0b2efa5976923b071f9b.ppt

  • Количество слайдов: 95

The Metric System Meters, Grams and Liters The Metric System Meters, Grams and Liters

Types of Data Qualitative data - Senses are used to collect data; information about Types of Data Qualitative data - Senses are used to collect data; information about qualities ² Examples: The color of the sky, hardness of a solid, appearance o an object Quantitative data - Measurements and numerical values are collected ² Examples: The age of your car, hours you studied, a solution is 27 o. C

Qualitative or Quantitative Data? 1) Carpet smells old and musty 2) Cat weighs 15 Qualitative or Quantitative Data? 1) Carpet smells old and musty 2) Cat weighs 15 pounds 3) Hot day 4) Softness of a kitten 5) The room temperature is 60 o. C

Units of Measurement: Compare an unknown quantity with one that is known A Quantitative Units of Measurement: Compare an unknown quantity with one that is known A Quantitative measurement consists of two parts A number A unit Both parts must be present for the measurement to be meaningful. Example: 20 grams

Do Now Why do we use scientific notation? • Large and small numbers can Do Now Why do we use scientific notation? • Large and small numbers can be written in shorthand form Ø This makes it easier to see the number clearly and work with

Section 2. 1 Section 2. 1

• The width of a DNA helix is – 0. 000034 meters or • The width of a DNA helix is – 0. 000034 meters or 34 angstroms • When discussing the large amount of the US debt $17, 000, 000 • Distance between Earth and Sun 92, 960, 000 miles

Using Scientific Notation • If the decimal point is moved to the left, the Using Scientific Notation • If the decimal point is moved to the left, the power of 10 is positive. 345 = 3. 45 × 102 • If the decimal point is moved to the right, the power of 10 is negative. 0. 0671 = 6. 71 × 10– 2

Concept Check Write 7, 882, 000 in scientific notation. Answer: 7. 882 × 106 Concept Check Write 7, 882, 000 in scientific notation. Answer: 7. 882 × 106 Copyright © Cengage Learning. All rights reserved

Concept Check Write 0. 0000000496 in scientific notation. Answer: 4. 96 × 10– 8 Concept Check Write 0. 0000000496 in scientific notation. Answer: 4. 96 × 10– 8 Copyright © Cengage Learning. All rights reserved

Concept Check Write 2. 32 × 10– 5 in standard notation. Answer: 0. 0000232 Concept Check Write 2. 32 × 10– 5 in standard notation. Answer: 0. 0000232 Copyright © Cengage Learning. All rights reserved

Calculations with Scientific Notation 1. Addition/subtraction 2. Multiplication 3. Division Calculations with Scientific Notation 1. Addition/subtraction 2. Multiplication 3. Division

Addition/subtraction with Scientific Notation • Move the decimal point to the left to INCREASE Addition/subtraction with Scientific Notation • Move the decimal point to the left to INCREASE the exponent • Move the decimal point to the right to DECREASE the exponent 1) (7. 0 x 103) + (2. 0 x 104) 2) (2. 9 x 103) – (3. 0 x 102)

Multiplication/Division with Scientific Notation 1) (5. 0 x 104)(4. 2 x 103) 2) 6. Multiplication/Division with Scientific Notation 1) (5. 0 x 104)(4. 2 x 103) 2) 6. 0 x 105 3. 0 x 102 3) 4. 8 x 10 -2 2. 0 x 10 -6

Section 2. 5 Significant Figures Significant figures – are the closest you can record Section 2. 5 Significant Figures Significant figures – are the closest you can record data to an actual measurement. Significant figures are used in: a)observations b) recording data c) calculations

Significant Figures Significant figures include: a) All the digits obtained from measurement, that you Significant Figures Significant figures include: a) All the digits obtained from measurement, that you are certain of b) One estimated digit, that you are not certain of (the uncertain)

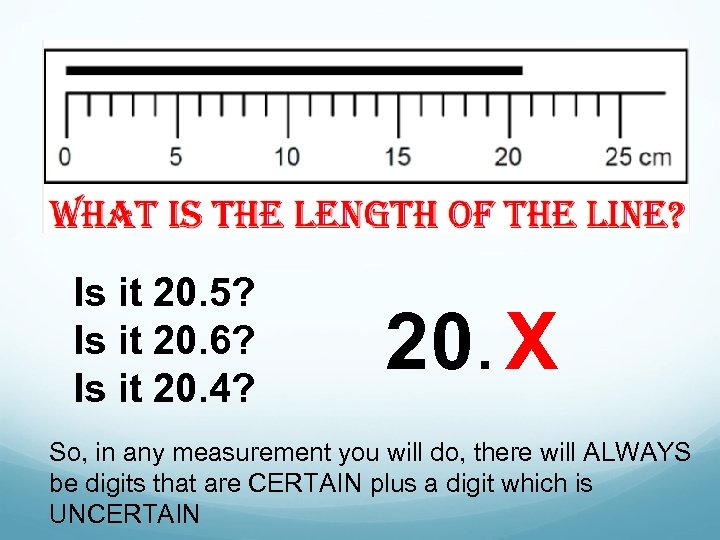Is it 20. 5? Is it 20. 6? Is it 20. 4? 20. X Is it 20. 5? Is it 20. 6? Is it 20. 4? 20. X So, in any measurement you will do, there will ALWAYS be digits that are CERTAIN plus a digit which is UNCERTAIN

Rules for Significant Figures 1) ALL non-zero numbers (1, 2, 3, 4, …) are Rules for Significant Figures 1) ALL non-zero numbers (1, 2, 3, 4, …) are ALWAYS significant. 1. 314 g ---> 4 significant figures 2) ALL zeroes which are to the left of nonzero digits are NOT significant. 0. 0025 ---> 2 s. f.

Rules for Significant Figures 3) ALL zeroes between non-zero numbers are ALWAYS significant. 1. Rules for Significant Figures 3) ALL zeroes between non-zero numbers are ALWAYS significant. 1. 008 ---> 4 s. f. 4) ALL zeroes which are to the right of the decimal point are ALWAYS significant. 500. 0 ---> 4 s. f. 500 ---> 1 s. f.

You try How many significant figures are there? a) 12. 5 b) 70. 52 You try How many significant figures are there? a) 12. 5 b) 70. 52 c) 0. 00604 d) 0. 896 e) 7200 f) 3001. 2 g) 450. 0

Do Now Perform the following calculation. 1. 4. 58 x 104 - 3. 2 Do Now Perform the following calculation. 1. 4. 58 x 104 - 3. 2 x 102 Determine the significant figures below. a) 4025 b) 0. 00041 c) 32, 780 d) 23. 0 e) 0. 00508

What is the importance of significant figures? • It is appreciated within the context What is the importance of significant figures? • It is appreciated within the context of recording and reporting of measurements. Ø Measurements which include linear measurements (length, width, height), temperature, volume, etc. • The number of significant figures in a number (representing a measurement) is indicative of the precision of the measurement made. Ø the more significant figures there are in a measurement, the more precise the measurement is. https: //www. youtube. com/watch? v=NJd. GCFrt. GCQ&index=2&list=PLr. FRJJM 2 is 57_Vi. H 9 Kxgf 101 QHR 2 Akt. Zl 4: 18 https: //www. youtube. com/watch? v=tf. Dtp. Ip 0 cu. E

Rounding with Significant Figures If the digit to be removed a. is less than Rounding with Significant Figures If the digit to be removed a. is less than 5, the preceding digit stays the same. Ex: 1. 33 rounds to 1. 3 b. is equal to or greater than 5, the preceding digit is increased by 1 Ex: 1. 36 rounds to 1. 4

Calculations with Significant Figures The resulting answer can never be more precise than the Calculations with Significant Figures The resulting answer can never be more precise than the least precise measurement in the calculation.

Significant Figures in Calculations 1. For addition or subtraction, your answer should have the Significant Figures in Calculations 1. For addition or subtraction, your answer should have the same number of decimal places as the measurement with the fewest decimal places. 23. 445 + 7. 83 31. 275 Copyright © Cengage Learning. All rights reserved Corrected 31. 28

Significant Figures in Calculations 2. For multiplication or division, the number of sig figs Significant Figures in Calculations 2. For multiplication or division, the number of sig figs in the result is the same as that in the measurement with the smallest number of significant figures. 1. 342 × 5. 5 7. 381 7. 4 Copyright © Cengage Learning. All rights reserved

Try 4. 38 -1. 2596 13. 1__ 3. 9473 Try 4. 38 -1. 2596 13. 1__ 3. 9473

Units of Measurements – mass, length, time, temperature etc. Different systems were adopted in Units of Measurements – mass, length, time, temperature etc. Different systems were adopted in different parts of the world. English system Metric system

Units of Measurement In 1960, an international agreement set up a system of units Units of Measurement In 1960, an international agreement set up a system of units called the International System or the SI system. This system is based on the metric system and units derived from the metric system. International Union of Pure and Applied Chemistry

Section 2. 2 SI Units Section 2. 2 SI Units

Volume Measure of the amount of 3 -D space occupied by a substance. SI Volume Measure of the amount of 3 -D space occupied by a substance. SI unit = cubic meter (m 3) Commonly measure solid volume in cm 3. 1 m. L = 1 cm 3 1 L = 1 dm 3 Copyright © Cengage Learning. All rights reserved

Meters measure length or distance One millimeter is about the thickness of a dime. Meters measure length or distance One millimeter is about the thickness of a dime.

Meters One centimeter is about the width of a large paper clip • or Meters One centimeter is about the width of a large paper clip • or your fingernail.

Which unit would you use to measure the length of this bicycle? km m Which unit would you use to measure the length of this bicycle? km m X cm mm

Which unit would you use to measure the mass of a penny? km g Which unit would you use to measure the mass of a penny? km g X c. L mg

Which unit would you use to measure the water in an aquarium? L X Which unit would you use to measure the water in an aquarium? L X m c. L mg

Which unit would you use to measure the mass of a feather? L m Which unit would you use to measure the mass of a feather? L m c. L mg X

Which unit would you use to measure the mass of a student desk? kg Which unit would you use to measure the mass of a student desk? kg X g c. L mg

Which unit would you use to measure the mass of an egg? kg g Which unit would you use to measure the mass of an egg? kg g X mm mg

Which unit would you use to measure this glass of milk? k. L L Which unit would you use to measure this glass of milk? k. L L c. L X m. L

Which unit would you use to measure the distance across Kansas? km X m Which unit would you use to measure the distance across Kansas? km X m cm m. L

Which unit would you use to measure the length of an atom. kg g Which unit would you use to measure the length of an atom. kg g ng X mg

Dimensional Analysis Dimensional Analysis

Dimensional Analysis Factor Label Method is a mathematical technique that allows you to use Dimensional Analysis Factor Label Method is a mathematical technique that allows you to use units to solve problems involving measurements. - method of converting one unit to another unit.

If you think about any number of everyday situations, you will realize that If you think about any number of everyday situations, you will realize that a quantity can usually be expressed in several different ways. For example: 1 dollar = 4 quarters = 10 dimes = 20 nickels = 100 pennies These are all expressions, or measurements, of the same amount of money.

The same thing is true of scientific quantities. For example: 1 meter = The same thing is true of scientific quantities. For example: 1 meter = 10 decimeters = 100 centimeters = 1000 millimeters These are different ways to express the same length.

Dimensional Analysis Conversion factors – is a ratio of equivalent values used to express Dimensional Analysis Conversion factors – is a ratio of equivalent values used to express the same quantity in different units *Conversion factors only change the units of a quantity without changing its value

Examples of Conversion Factors 1 inch 2. 54 cm 1 day 24 hrs 1, Examples of Conversion Factors 1 inch 2. 54 cm 1 day 24 hrs 1, 000 m 1 km 2. 54 cm 1 inch 24 hrs 1 day 1 km 1, 000 m

Derived Units Derived Unit -unit that is define by a combination of base units. Derived Units Derived Unit -unit that is define by a combination of base units. q Speed -Measured in (m/s) or (length/time) q Volume - Measured in (m 3) or length*width*height q Density -Measured in g/cm 3 or mass/volume

Ex. 1 How many minutes are in 24 hours? Ex. 1 How many minutes are in 24 hours?

Ex. 2 How many cups are in a 2 L bottle of soda? (1 Ex. 2 How many cups are in a 2 L bottle of soda? (1 quart = 4 cups , 1. 06 quarts = 1 L)

Ex 3 How many baseball bats can be found in 2 stadiums? 1 stadium Ex 3 How many baseball bats can be found in 2 stadiums? 1 stadium = 46 players 5 gloves = 10 baseballs 2 players = 3 bats

Why is dimensional analysis important? Its important because we need answers that are universally Why is dimensional analysis important? Its important because we need answers that are universally accepted and meaningful. For example, 1 foot translates to 12 inches, which translates to 30. 48 centimeters. This is the same length said in three different "languages" (or units, in this case). The key point is that they all refer to the same thing.

If you ever need to figure out how much carpet to buy for If you ever need to figure out how much carpet to buy for your living room, how much it will cost, or how long it will take to travel somewhere, you can use dimensional analysis. If you have a prescription for 5, 000 mg of medicine, and upon getting it filled, the dosage reads 5 g of medicine, did the pharmacist make a mistake?

The Metric System The metric system is a measurement system based on our decimal The Metric System The metric system is a measurement system based on our decimal (base 10) number system. Other countries and all scientists and engineers use the metric system for measurement.

Using SI Units of Length Commonly Used Metric Prefixes Prefix Symbol Factor mega M Using SI Units of Length Commonly Used Metric Prefixes Prefix Symbol Factor mega M 106 kilo k 103 deci d 10 -1 centi c 10 -2 milli m 10 -3 micro μ 10 -6 nano n 10 -9 pico p 10 -12

Ex. 1 Convert 3 kilometers to meters. Ex. 1 Convert 3 kilometers to meters.

Ex. 2 Convert 5, 000 millimeters to meters. Ex. 2 Convert 5, 000 millimeters to meters.

Try 1) Convert 22, 000 centimeters to meters. 2) Convert 5. 5 x 105 Try 1) Convert 22, 000 centimeters to meters. 2) Convert 5. 5 x 105 nanograms to grams. 3) Convert 1. 5 x 104 grams to kilograms.

Ex. 1 Convert 3, 500 millimeters to centimeters. C. F. Known unit Base unit Ex. 1 Convert 3, 500 millimeters to centimeters. C. F. Known unit Base unit Unknown unit

Ex. 2 Convert 3. 5 x 107 μg to cg. Ex. 2 Convert 3. 5 x 107 μg to cg.

Ex. 3 Convert 4. 2 x 108 cg to Mg Ex. 3 Convert 4. 2 x 108 cg to Mg

Density is the ratio of the mass of an object to its volume mass Density is the ratio of the mass of an object to its volume mass Density = volume - The relationship between an object’s mass and its volume tells you whether it will float or sink. This relationship is called density. .

Density This figure compares the density of four substances: lithium, water, aluminum, and lead. Density This figure compares the density of four substances: lithium, water, aluminum, and lead. Increasing density (mass per unit volume) 10 g 19 cm 3 10 g 10 cm 3 0. 53 g/cm 3 1. 0 g/cm 3 10 g 3. 7 cm 3 10 g 0. 88 cm 3 2. 7 g/cm 3 11. 4 g/cm 3

Ex. 1 What is the volume of a pure silver coin that has a Ex. 1 What is the volume of a pure silver coin that has a mass of 14 g? The density of silver (Ag) is 10. 5 g/cm 3.

Ex. 2 A piece of wood that measures 3. 0 cm by 6. 0 Ex. 2 A piece of wood that measures 3. 0 cm by 6. 0 cm by 4. 0 cm has a mass of 80. 0 grams. What is the density of the wood? Would the piece of wood float in water?

What’s the forecast for tomorrow— hot or cold? Will the high temperature tomorrow be What’s the forecast for tomorrow— hot or cold? Will the high temperature tomorrow be 28°C, which is very warm? Or 28°F, which is very cold? Without the correct units, you can’t be sure.

Temperature Scales Scientists commonly use two equivalent units of temperature, the degree Celsius and Temperature Scales Scientists commonly use two equivalent units of temperature, the degree Celsius and the kelvin.

Temperature Scales Temperature is a measure of how hot or cold an object is. Temperature Scales Temperature is a measure of how hot or cold an object is. An object’s temperature determines the direction of heat transfer. When two objects at different temperatures are in contact, heat moves from the object at the higher temperature to the object at the lower temperature.

Temperature Scales The Celsius scale sets the freezing point of water at 0°C and Temperature Scales The Celsius scale sets the freezing point of water at 0°C and the boiling point of water at 100°C. The distance between these two fixed points is divided into 100 equal intervals, or degrees Celsius (°C).

Temperature Scales Another temperature scale used in the physical sciences is the Kelvin, or Temperature Scales Another temperature scale used in the physical sciences is the Kelvin, or absolute, scale. This scale is named for Lord Kelvin (1824– 1907), a Scottish physicist. On the Kelvin scale, the freezing point of water is 273. 15 kelvins (K), and the boiling point is 373. 15 (K). Note that with the Kelvin scale, the degree sign is not used.

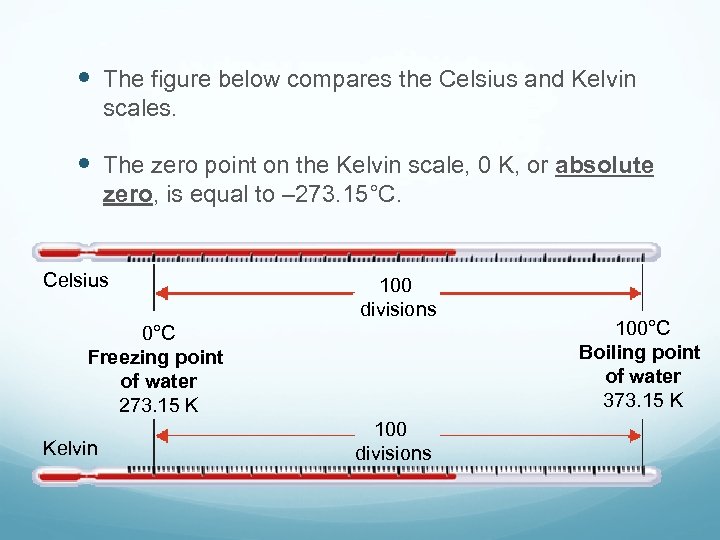The figure below compares the Celsius and Kelvin scales. The zero point on The figure below compares the Celsius and Kelvin scales. The zero point on the Kelvin scale, 0 K, or absolute zero, is equal to – 273. 15°C. Celsius 100 divisions 0°C Freezing point of water 273. 15 K Kelvin 100 divisions 100°C Boiling point of water 373. 15 K

Converting between Celsius and Kelvin K = °C + 273 °C = K – Converting between Celsius and Kelvin K = °C + 273 °C = K – 273

END END

Changing Metric Units To change from one unit to another in the metric system Changing Metric Units To change from one unit to another in the metric system you simply multiply or divide by a power of 10.

To change from a larger unit to a smaller unit, you need to multiply. To change from a larger unit to a smaller unit, you need to multiply. 1 km x 1000 = 1000 m 1 m x 100 = 100 cm 1 cm x 10 = 10 mm

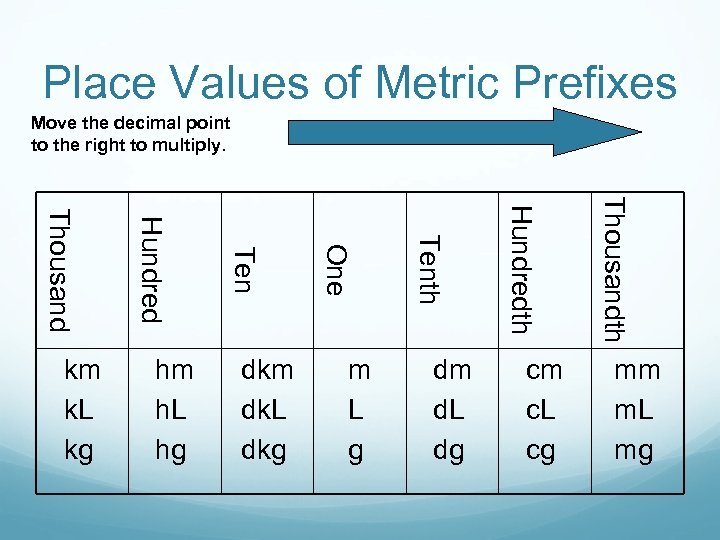Place Values of Metric Prefixes Move the decimal point to the right to multiply. Place Values of Metric Prefixes Move the decimal point to the right to multiply. cm c. L cg Thousandth dm d. L dg Hundredth m L g Tenth dkm dk. L dkg One hm h. L hg Ten Hundred Thousand km k. L kg mm m. L mg

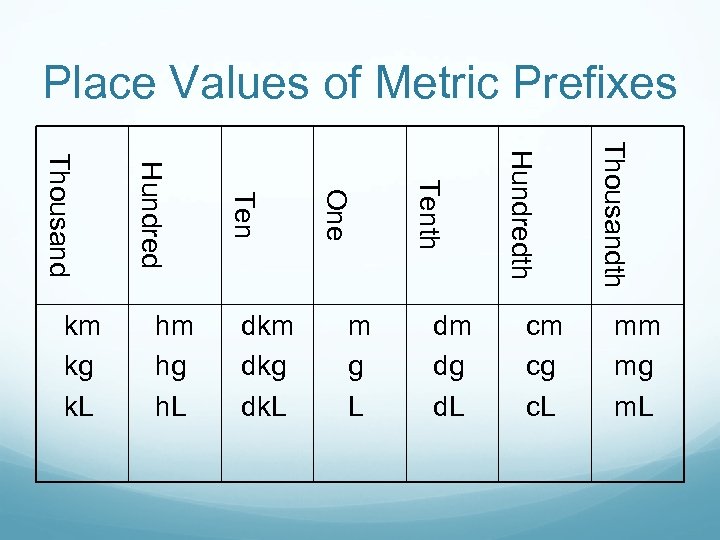Place Values of Metric Prefixes cm cg c. L Thousandth dm dg d. L Place Values of Metric Prefixes cm cg c. L Thousandth dm dg d. L Hundredth m g L Tenth dkm dkg dk. L One hm hg h. L Ten Hundred Thousand km kg k. L mm mg m. L

To change from smaller units to larger units you divide by a power of To change from smaller units to larger units you divide by a power of ten. 1000 mm ÷ 10 = 100 cm ÷ 10 = 10 dm ÷ 10 = 1 m

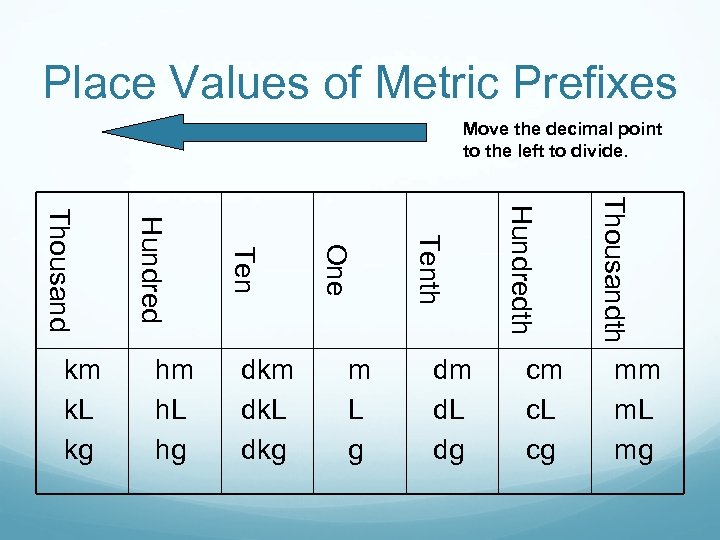Place Values of Metric Prefixes Move the decimal point to the left to divide. Place Values of Metric Prefixes Move the decimal point to the left to divide. cm c. L cg Thousandth dm d. L dg Hundredth m L g Tenth dkm dk. L dkg One hm h. L hg Ten Hundred Thousand km k. L kg mm m. L mg

Converting Metric Units k h dk Base unit d c m King Henry Died Converting Metric Units k h dk Base unit d c m King Henry Died By Drinking Chocolate Milk

Converting Metric Units 1) 43. 976 hg = ______ dg 2) 0. 0009586 ks Converting Metric Units 1) 43. 976 hg = ______ dg 2) 0. 0009586 ks = _____ms 3) 900005 m. L= ______DL 4) 65. 93280 m = ______cm 5) 52. 3 cm = _______ μm

Uncertainty in Measurements There is a limit to the accuracy of any measurement. The Uncertainty in Measurements There is a limit to the accuracy of any measurement. The digit that must be estimated is called uncertain A measurement always has some degree of uncertainty We usually report a measurement by recording all the certain digits plus the first uncertain digit (Significant figures)

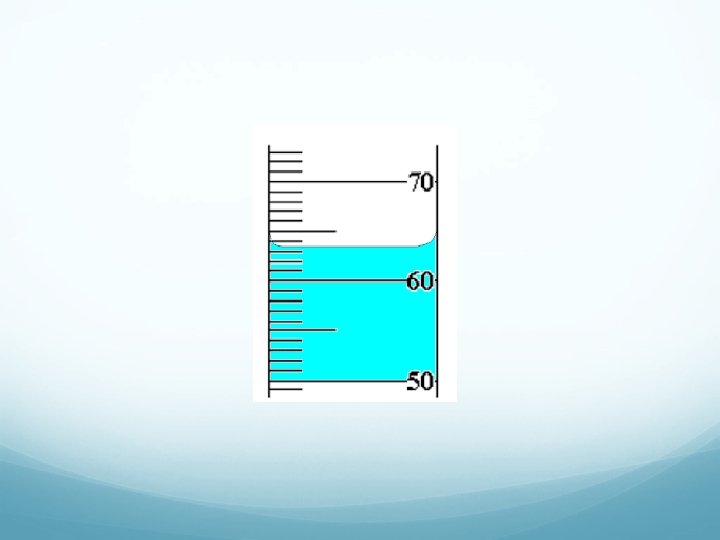
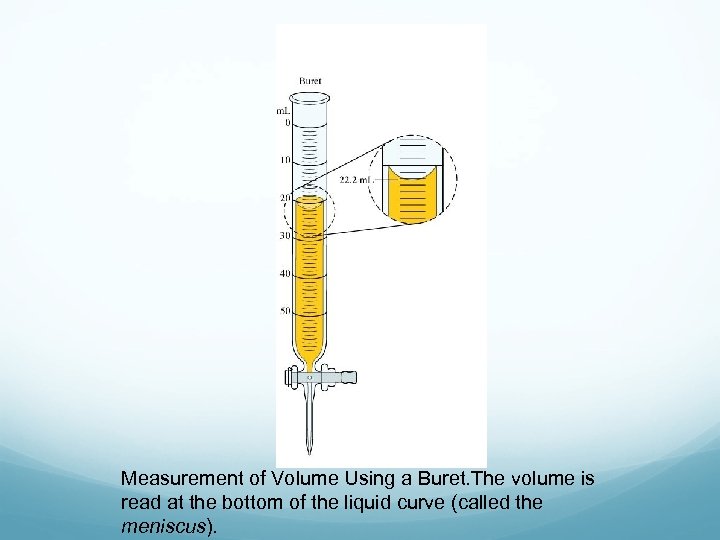Measurement of Volume Using a Buret. The volume is read at the bottom of Measurement of Volume Using a Buret. The volume is read at the bottom of the liquid curve (called the meniscus).

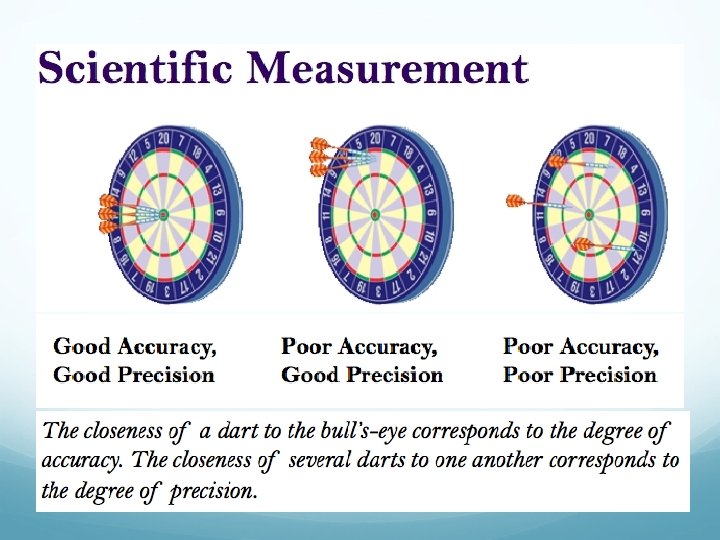
The Difference between Precision and Accuracy The Difference between Precision and Accuracy

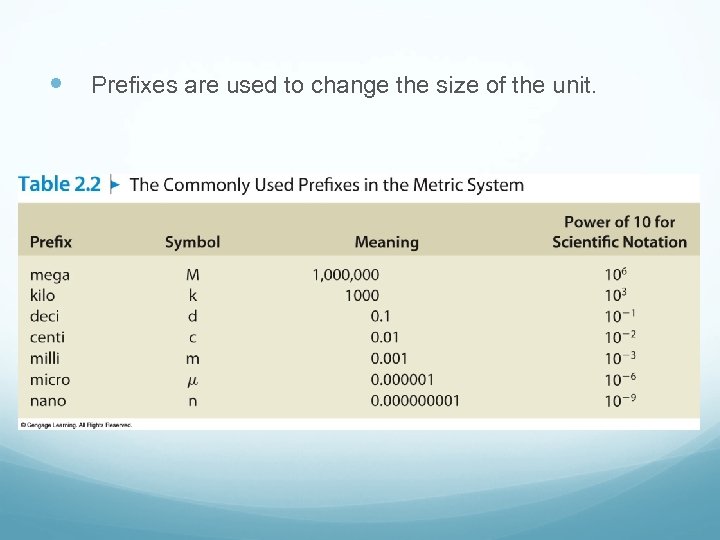Prefixes are used to change the size of the unit. Prefixes are used to change the size of the unit.