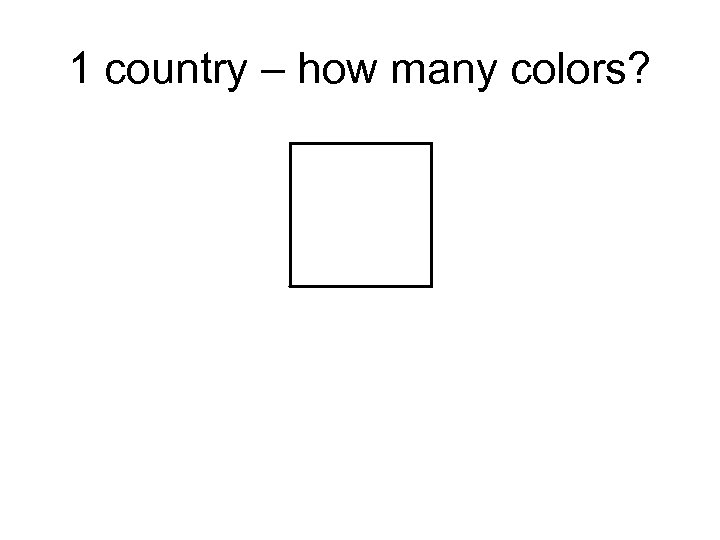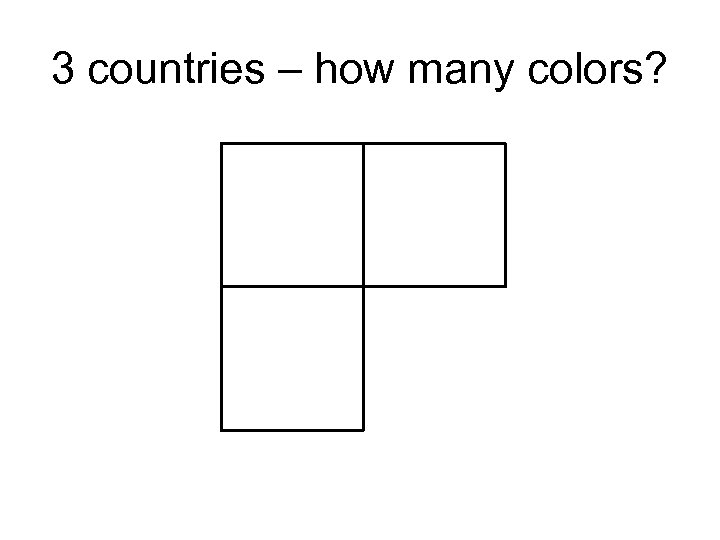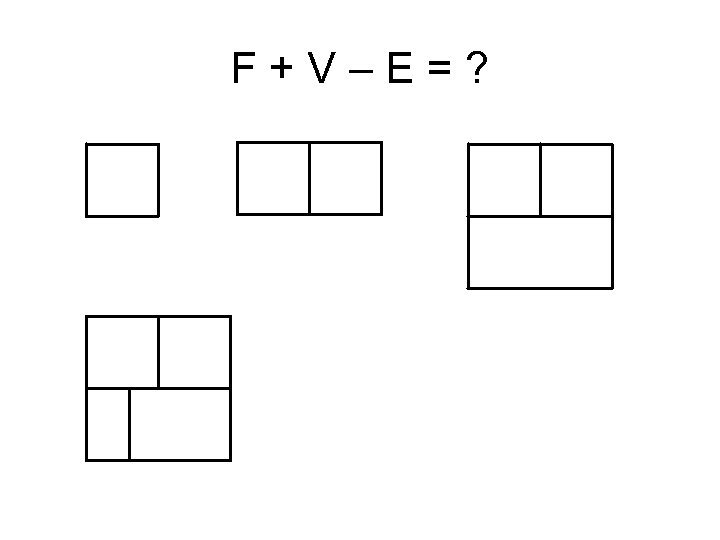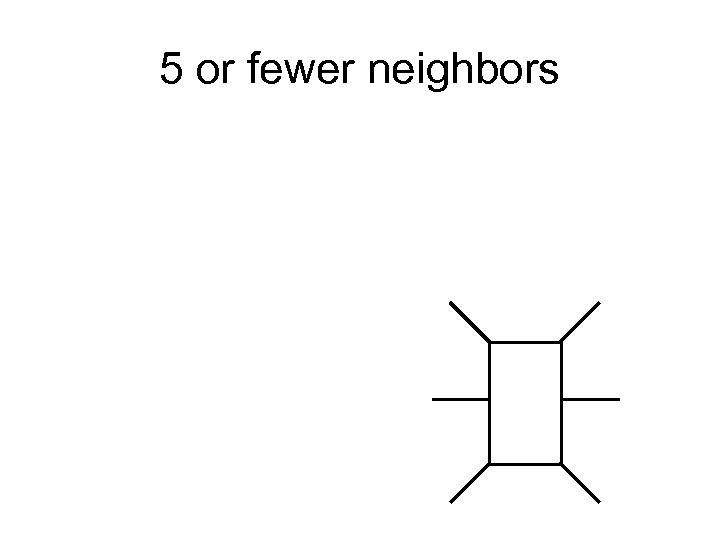The Mathematics of Map Coloring – The Four-Color Theorem
The Mathematics of Map Coloring – The Four-Color Theorem
 The Problem
The Problem
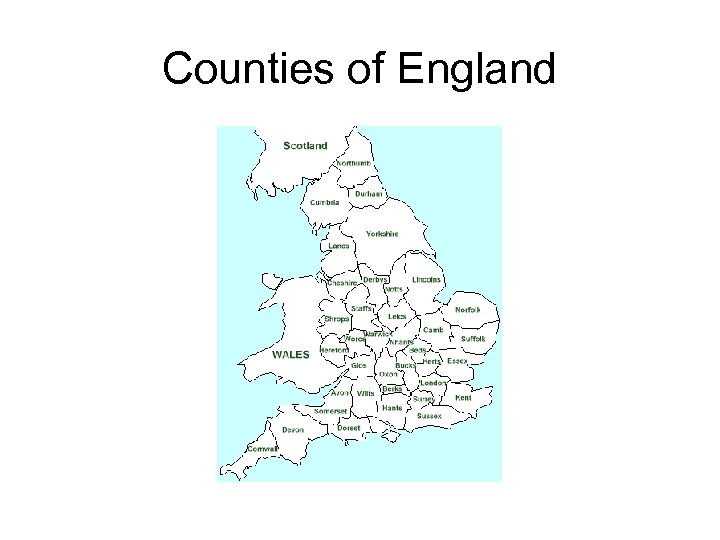 Counties of England
Counties of England
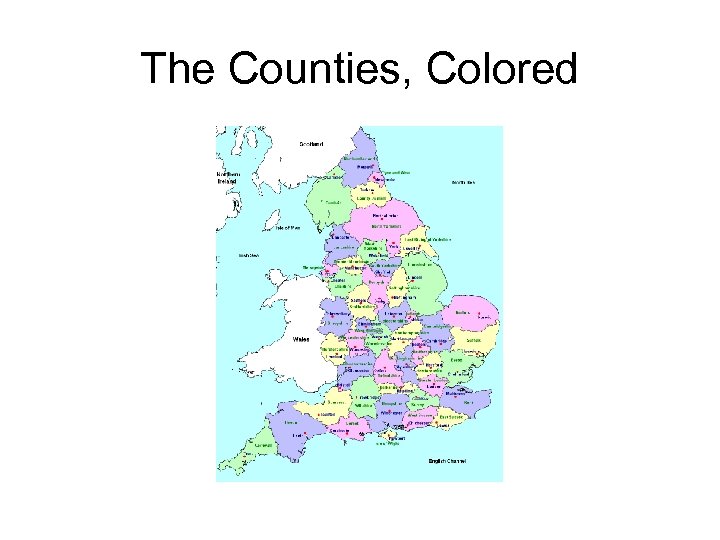 The Counties, Colored
The Counties, Colored
 Why Counties of England?
Why Counties of England?
 1852 October 23
1852 October 23
 How to begin?
How to begin?
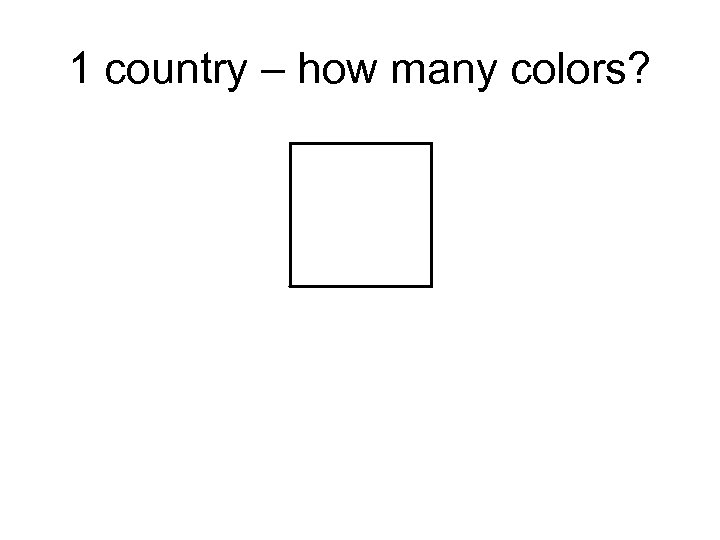 1 country – how many colors?
1 country – how many colors?
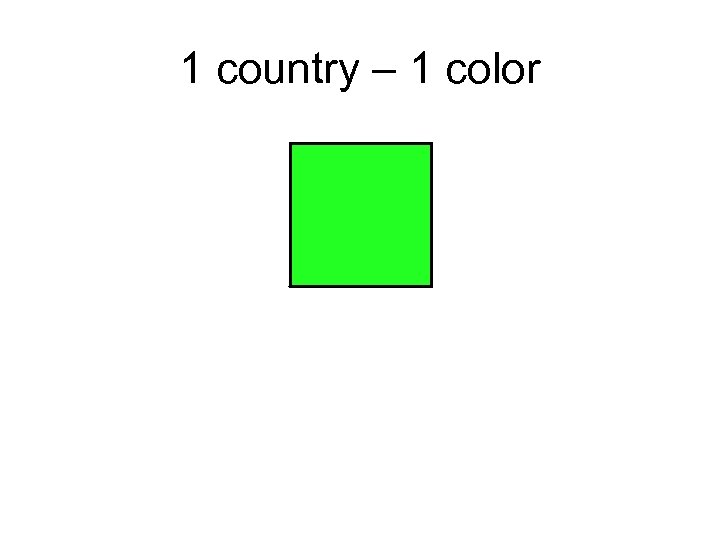 1 country – 1 color
1 country – 1 color
 2 countries – how many colors?
2 countries – how many colors?
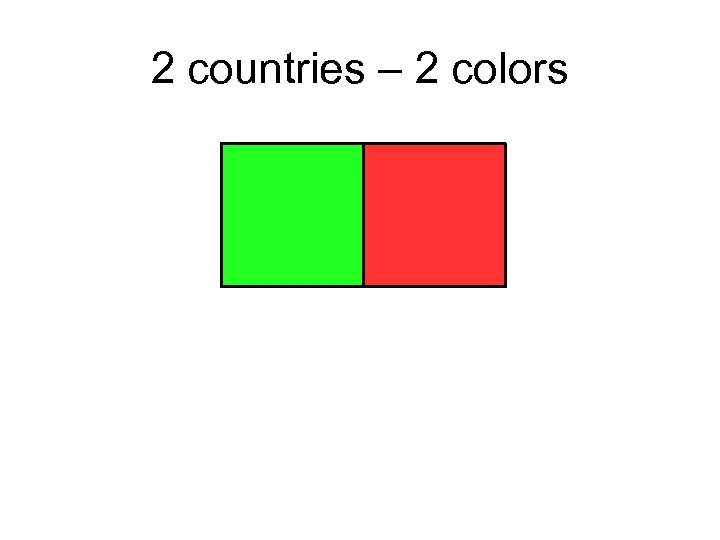 2 countries – 2 colors
2 countries – 2 colors
 3 countries – how many colors?
3 countries – how many colors?
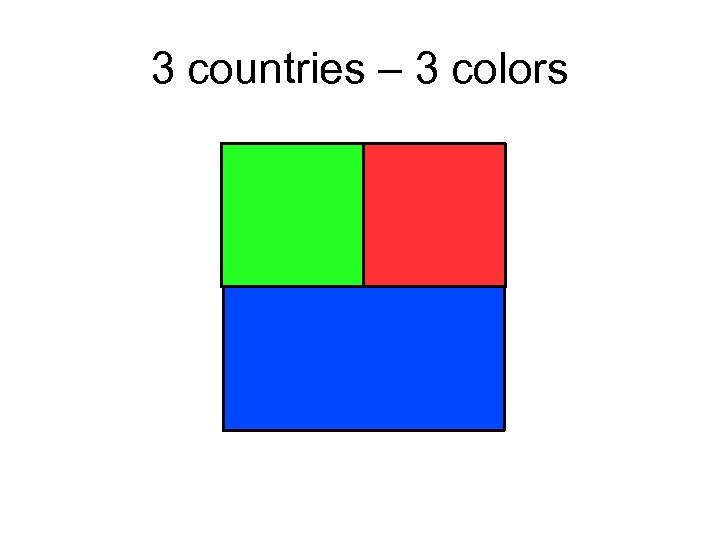 3 countries – 3 colors
3 countries – 3 colors
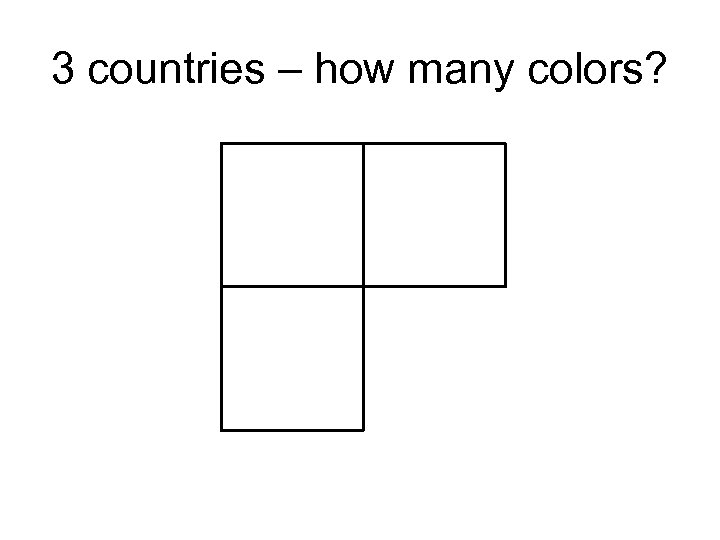 3 countries – how many colors?
3 countries – how many colors?
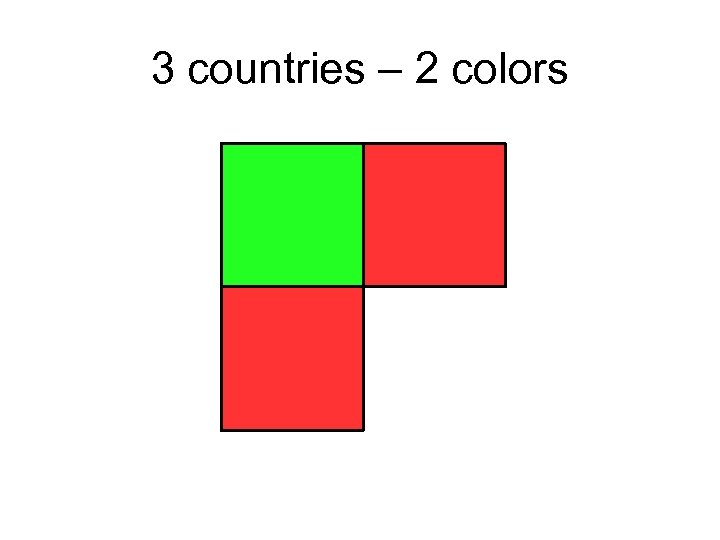 3 countries – 2 colors
3 countries – 2 colors
 4 countries – how many colors?
4 countries – how many colors?
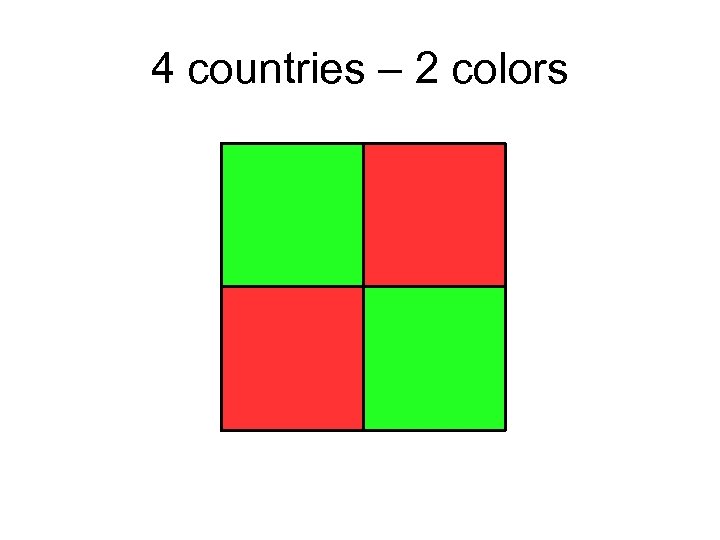 4 countries – 2 colors
4 countries – 2 colors
 4 countries – how many colors?
4 countries – how many colors?
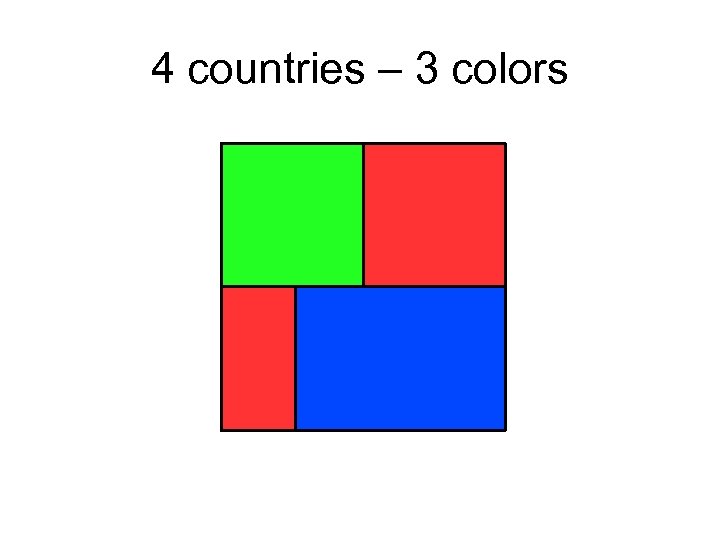 4 countries – 3 colors
4 countries – 3 colors
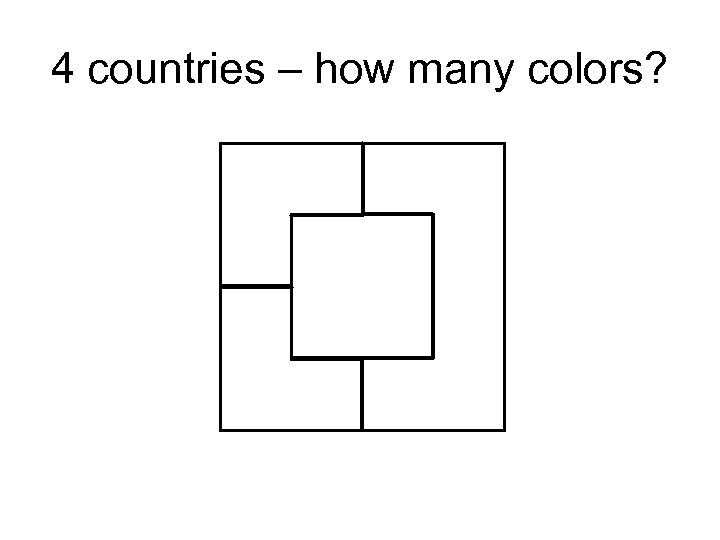 4 countries – how many colors?
4 countries – how many colors?
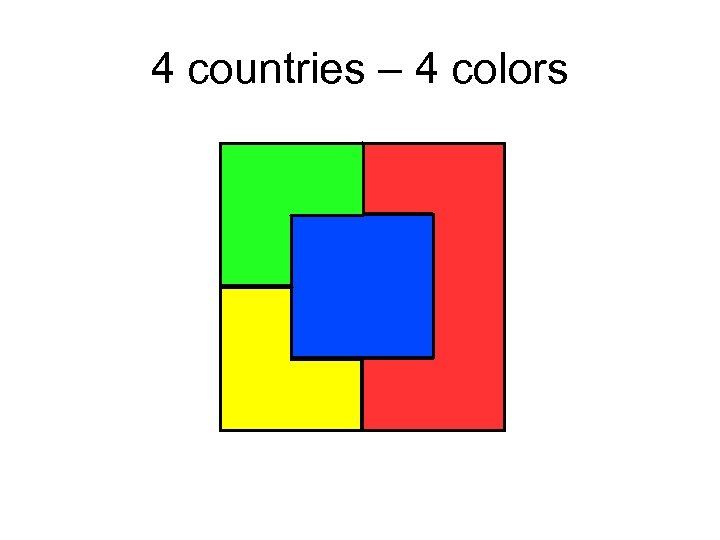 4 countries – 4 colors
4 countries – 4 colors
 Important fact
Important fact
 Do the math
Do the math
 Leonhard Euler (1707 -83)
Leonhard Euler (1707 -83)
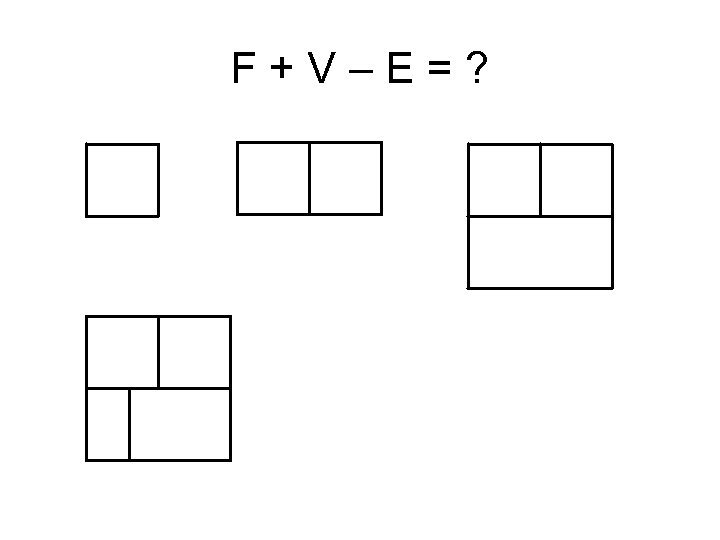 F+V–E=?
F+V–E=?
 Euler Characteristic
Euler Characteristic
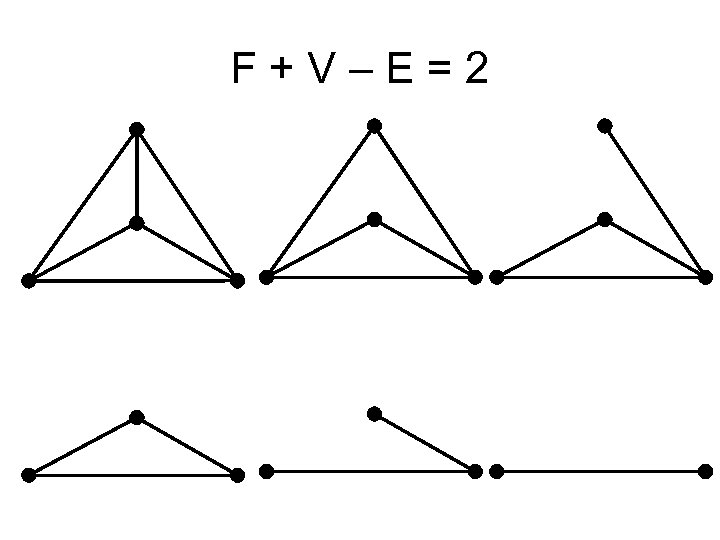 F+V–E=2
F+V–E=2
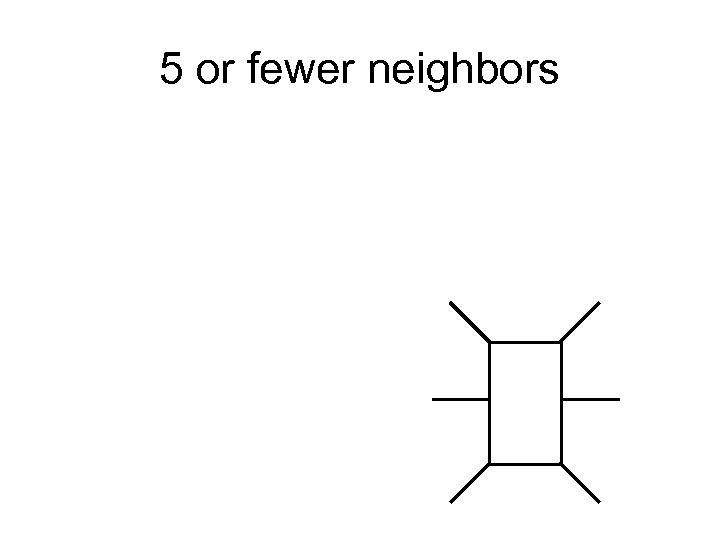 5 or fewer neighbors
5 or fewer neighbors
 5 or fewer neighbors
5 or fewer neighbors
 5 or fewer neighbors
5 or fewer neighbors
 5 or fewer neighbors
5 or fewer neighbors
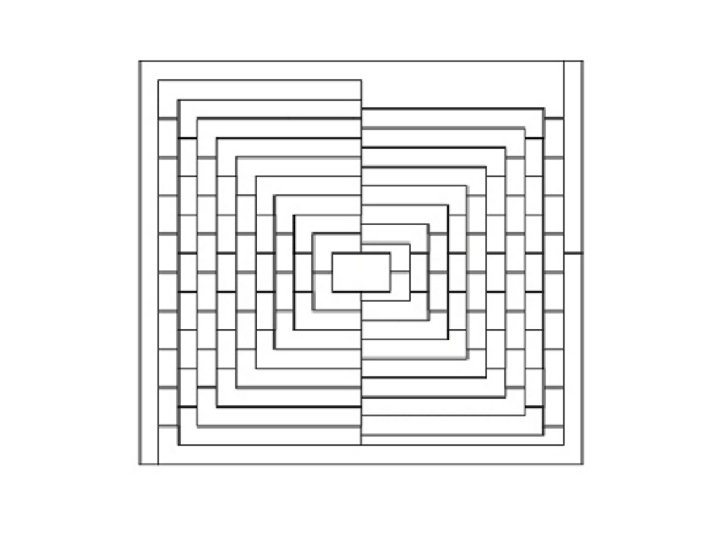
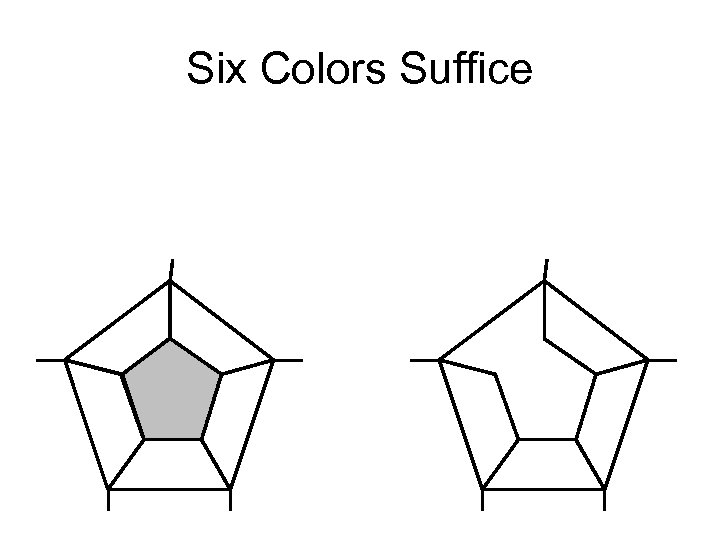
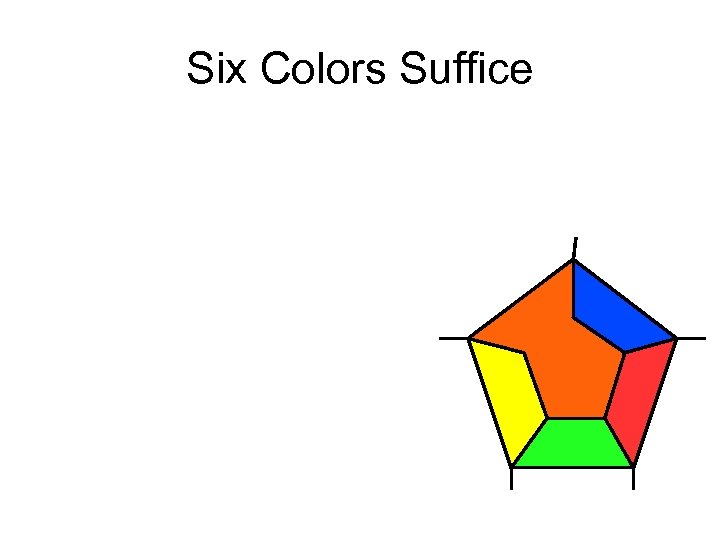
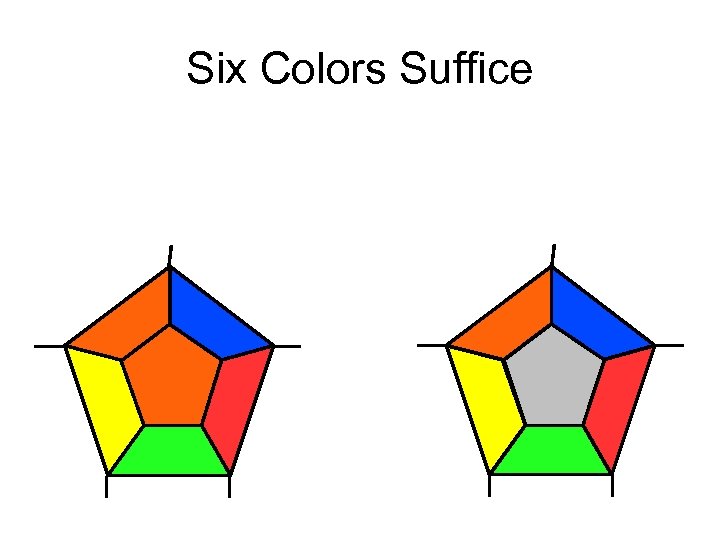
 Six Colors Suffice
Six Colors Suffice
 Six Colors Suffice
Six Colors Suffice
 Six Colors Suffice
Six Colors Suffice
 Six Colors Suffice
Six Colors Suffice
 Six Colors Suffice
Six Colors Suffice
 Pick a number: 4, 5, or 6?
Pick a number: 4, 5, or 6?
 Break time
Break time
 No activity for several decades
No activity for several decades
 Solved, at last
Solved, at last
 How did he do it?
How did he do it?
 Is this approach familiar?
Is this approach familiar?
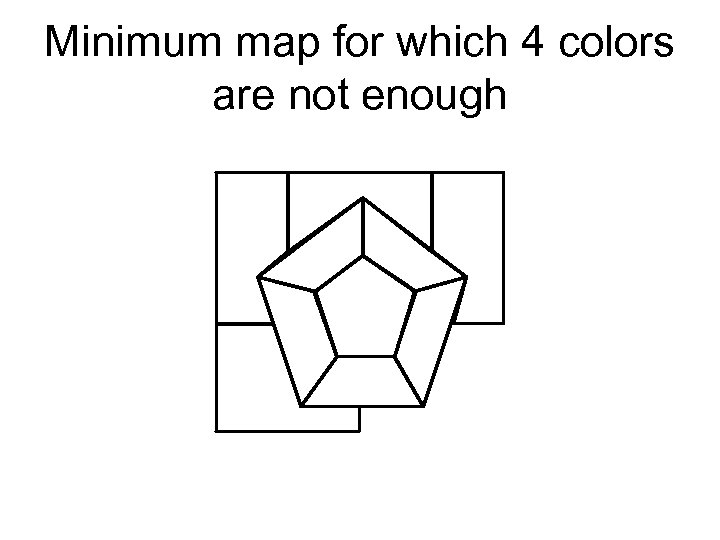 Minimum map for which 4 colors are not enough
Minimum map for which 4 colors are not enough
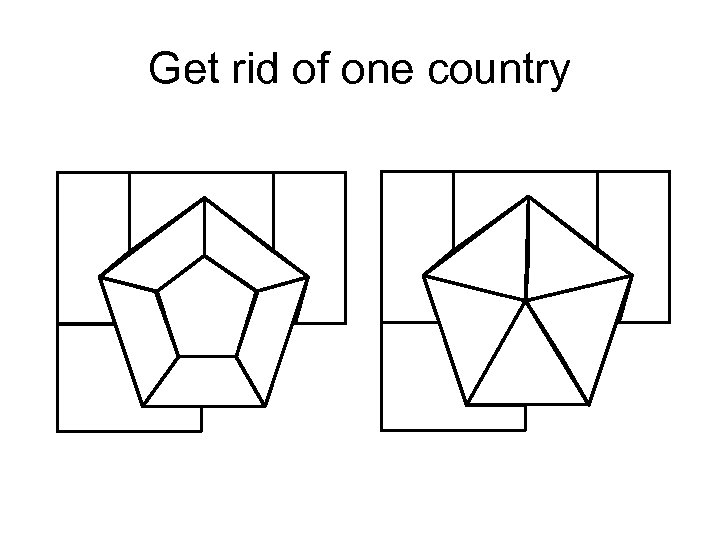 Get rid of one country
Get rid of one country
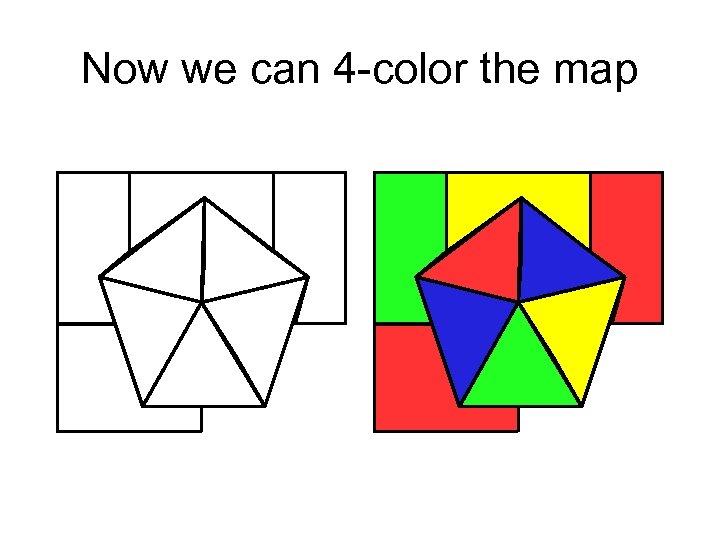 Now we can 4 -color the map
Now we can 4 -color the map
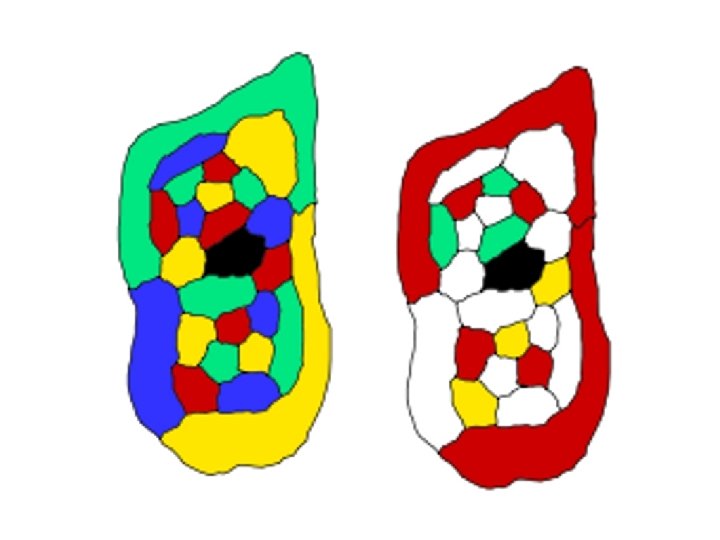
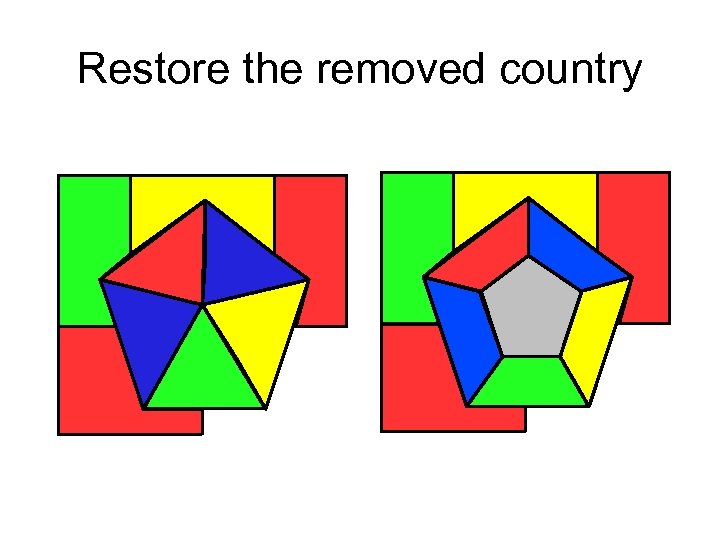 Restore the removed country
Restore the removed country
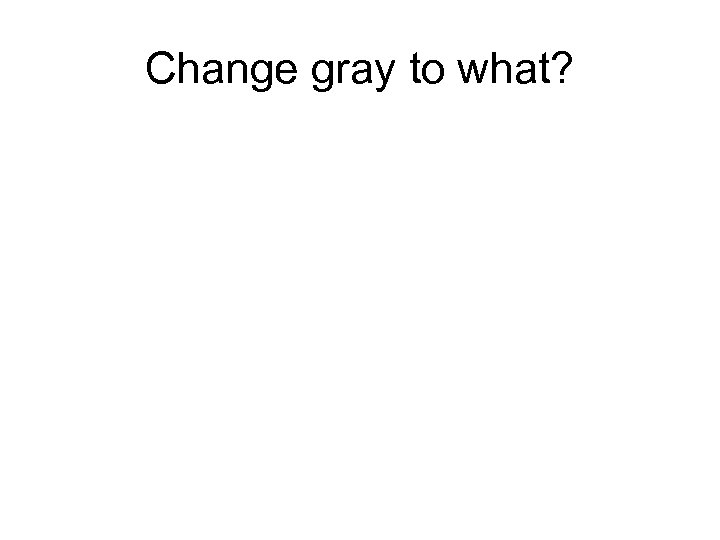 Change gray to what?
Change gray to what?
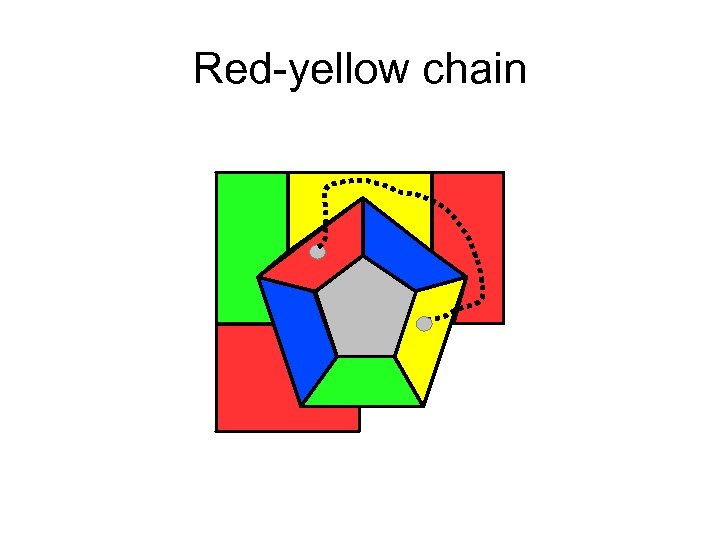 Red-yellow chain
Red-yellow chain
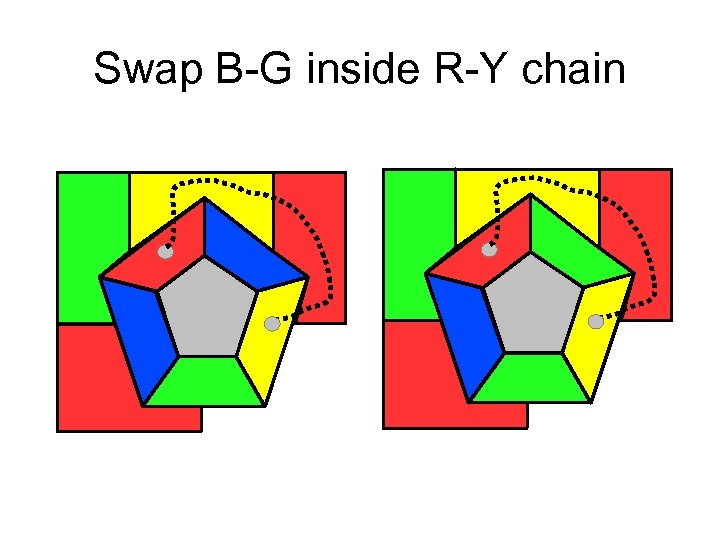 Swap B-G inside R-Y chain
Swap B-G inside R-Y chain
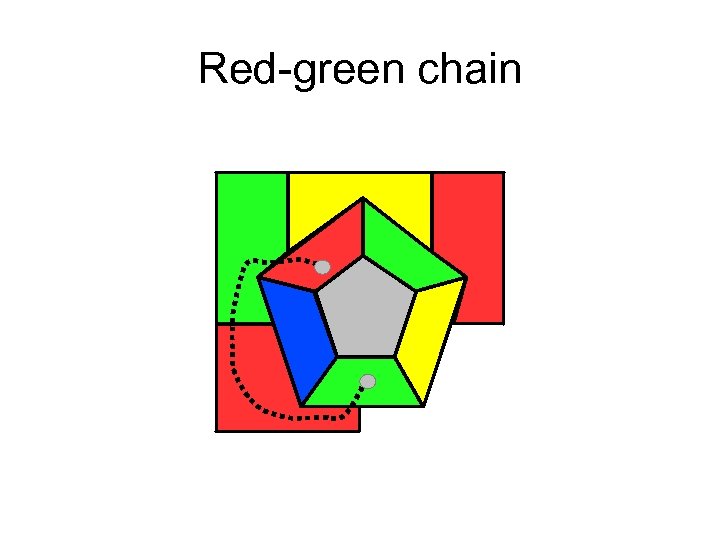 Red-green chain
Red-green chain
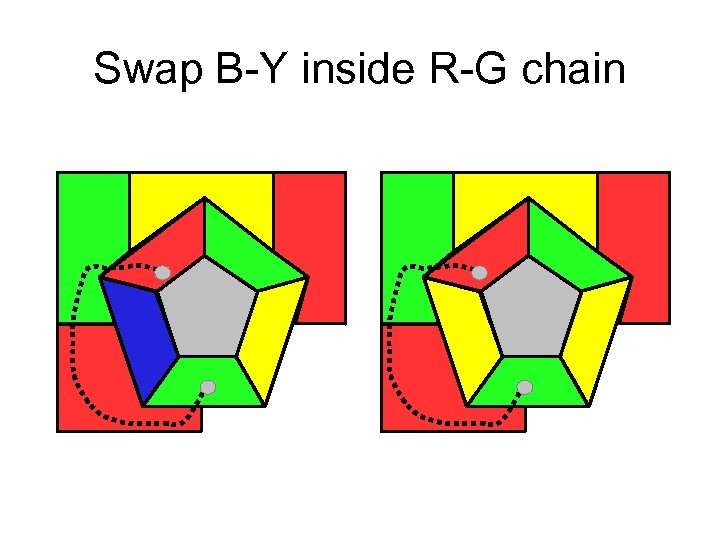 Swap B-Y inside R-G chain
Swap B-Y inside R-G chain
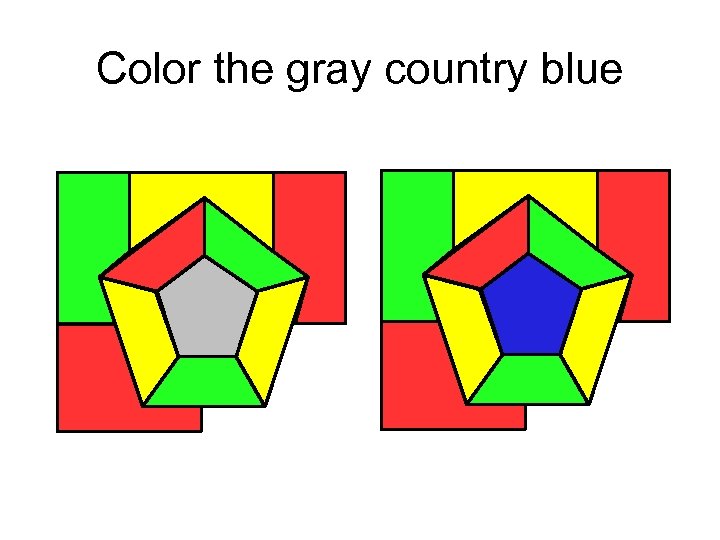 Color the gray country blue
Color the gray country blue
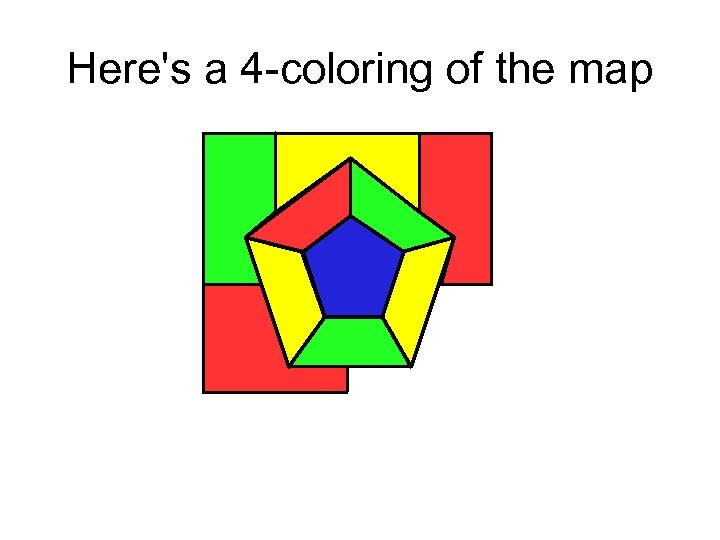 Here's a 4 -coloring of the map
Here's a 4 -coloring of the map
 Four Colors Suffice!
Four Colors Suffice!
 Hold it a second
Hold it a second
 Trouble in paradise
Trouble in paradise
 Ouch!
Ouch!
 The Five Color Theorem
The Five Color Theorem
 Maybe 4 colors aren't enough?
Maybe 4 colors aren't enough?
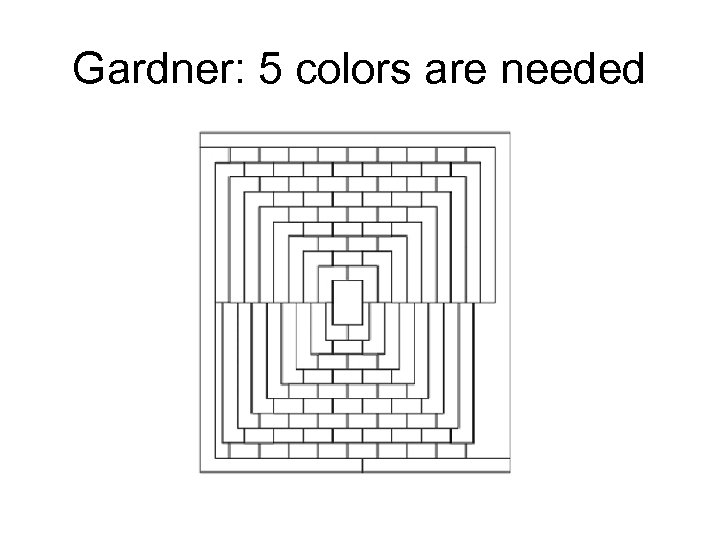 Gardner: 5 colors are needed
Gardner: 5 colors are needed
 80+ years had gone by. . .
80+ years had gone by. . .
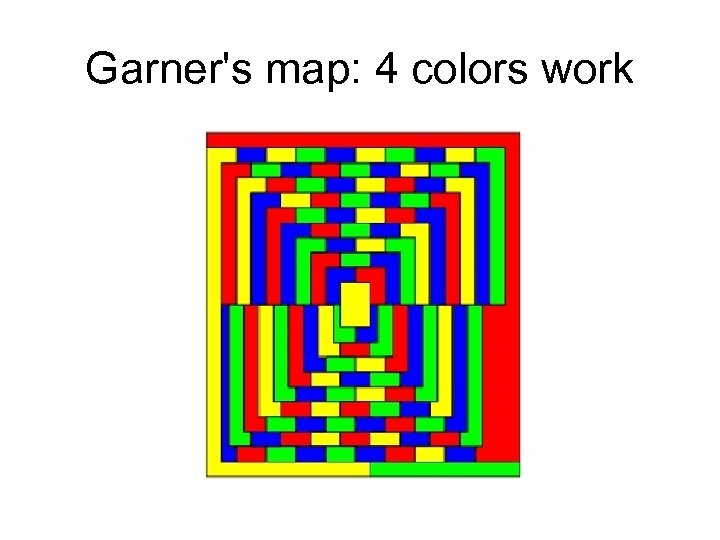 Garner's map: 4 colors work
Garner's map: 4 colors work
 At last!
At last!
 Some reactions
Some reactions
 What's the problem?
What's the problem?
 Eventually: Acceptance
Eventually: Acceptance
 In conclusion. . .
In conclusion. . .