Скачать презентацию The Leontief Input-Output Method Part 2 Example 1 Скачать презентацию The Leontief Input-Output Method Part 2 Example 1

61deaeff1bca901128a00d93aabca5f8.ppt

  • Количество слайдов: 24

The Leontief Input-Output Method, Part 2 Example 1: Sunny Summer Beverages produces and bottles The Leontief Input-Output Method, Part 2 Example 1: Sunny Summer Beverages produces and bottles a variety of fruit juices. For every dollar worth of juice it produces, it keeps $. 04 worth of juice in house to help keep the workers hydrated and happy. If the company produces $200 worth of juice, how much will be available for sale?

The Leontief Input-Output Method, Part 2 Example 1: Sunny Summer Beverages Recall that we The Leontief Input-Output Method, Part 2 Example 1: Sunny Summer Beverages Recall that we can calculate the Demand if we know the Production and the Consumption (. 04 in this case): P: Total Production P -. 04 P = D D: Demand. 96 P = D. 96(200) = $192 = D

The Leontief Input-Output Method, Part 2 We can modify this equation slightly to determine The Leontief Input-Output Method, Part 2 We can modify this equation slightly to determine the Demand for a 2 -sector economy. In this case, we’ll use the consumption matrix, C: P – CP = D

The Leontief Input-Output Method, Part 2 Example 2: ABC Furniture manufactures a variety of The Leontief Input-Output Method, Part 2 Example 2: ABC Furniture manufactures a variety of office furniture. It also manufactures bolts, some of which are used in its furniture. Every dollar worth of bolts produced requires an input of $. 03 worth of bolts and $. 02 worth of office furniture. Each dollar worth of office furniture requires an input of $. 04 worth of bolts and $. 05 worth of office furniture.

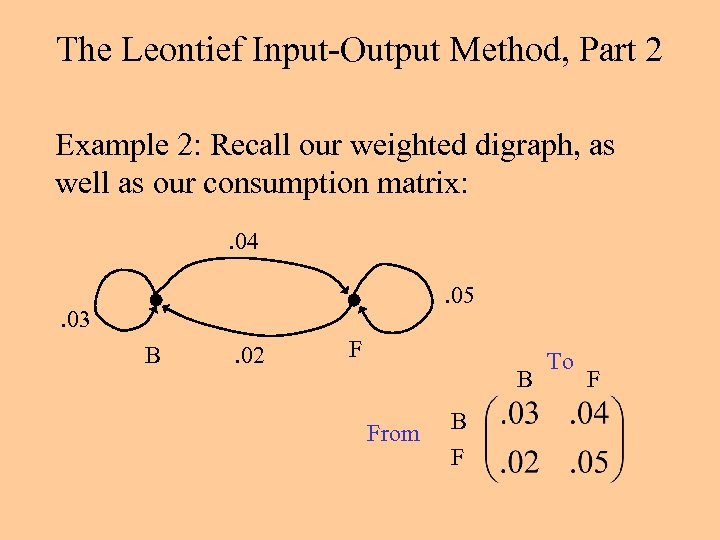The Leontief Input-Output Method, Part 2 Example 2: Recall our weighted digraph, as well The Leontief Input-Output Method, Part 2 Example 2: Recall our weighted digraph, as well as our consumption matrix: . 04. 05 . 03 B . 02 F B From B F To F

The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of bolts and $400 of office furniture. How much of each will be available for sale?

The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of bolts and $400 of office furniture. How much of each will be available for sale? P – CP = D - =

The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of The Leontief Input-Output Method, Part 2 Example 2: Suppose the company produces $300 of bolts and $400 of office furniture. How much of each will be available for sale? P – CP = D - = So $275 of bolts and $374 of office furniture available to sell.

The Leontief Input-Output Method, Part 2 Things get a little more interesting if we The Leontief Input-Output Method, Part 2 Things get a little more interesting if we know the demand need to determine the production. Start with our previous equation: P – CP = D

The Leontief Input-Output Method, Part 2 P – CP = D We would like The Leontief Input-Output Method, Part 2 P – CP = D We would like to factor out P on the left hand side of the equation, but it’s not quite as easy with a matrix as it is with a variable. First, we have to multiply P by the Identity matrix, I.

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D What is an Identity matrix? It assigns a coefficient of 1 to each variable. Then if you multiply I by any matrix, it returns the original matrix: IP = P

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D An Identity matrix is always a square matrix (2 x 2, 3 x 3, 4 x 4, etc. ). The diagonal starting in the 1 st row, 1 st column contains 1 s, with all other entries being 0 s.

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D Because most of our examples will involve two sectors, I will normally be 2 x 2:

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D Now we can factor out P: (I – C)P = D

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D (I – C)P = D If (I – C) represented variables, we could simply divide each side of the equation by (I – C) and be done. Because it is a matrix, however, we must multiply by the inverse matrix, (I – C)-1

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D (I – C)-1(I – C)P = (I – C)-1 D

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D (I – C)-1(I – C)P = (I – C)-1 D Fortunately, (I – C)-1 and (I – C) are inverses, so when we multiply them, they essentially eliminate each other.

The Leontief Input-Output Method, Part 2 P – CP = D IP – CP The Leontief Input-Output Method, Part 2 P – CP = D IP – CP = D (I – C)-1(I – C)P = (I – C)-1 D We finally get the equation we really want: P = (I – C)-1 D

The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order for $200 of bolts and $700 of office furniture, how much of each must it produce to fill the order?

The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order for $200 of bolts and $700 of office furniture, how much of each must it produce to fill the order? We are trying to find the production, P, in a two-sector economy, so we will use P = (I – C)-1 D

The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order for $200 of bolts and $700 of office furniture, how much of each must it produce to fill the order? P = (I – C)-1 D I= C= because of the two sectors. D=

The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order for $200 of bolts and $700 of office furniture, how much of each must it produce to fill the order? P = (I – C)-1 D = ( = ) -1

The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order The Leontief Input-Output Method, Part 2 Example 3: If ABC Furniture receives an order for $200 of bolts and $700 of office furniture, how much of each must it produce to fill the order? P = (I – C)-1 D = So the company must produce $236. 78 worth of bolts and $741. 83 worth of office furniture.