0e4cc010af9393dd0d51d0ba71bf1e9a.ppt
- Количество слайдов: 45

The k-server Problem Study Group: Randomized Algorithm Presented by Ray Lam August 16, 2003

Outline 1. 2. 3. Background and problem definition The Harmonic k-server Algorithm Proving the claimed performance of the algorithm 2

Background And Problem Definition

The Metric Space l Definition: A metric space M = (V, d) consists of a set of points V with a distance function d: V R satisfying the following properties: l l d(u, v) 0 for all u, v V. d(u, v) = 0 iff u = v. d(u, v) = d(v, u) for all u, v V. d(u, v) + d(v, w) d(u, w) for all u, v, w V. 4

The Metric Space l l Think of it as a complete weighted graph Weight corresponds to distance between points 3 1 2 4 1 3 2 2 1 2 5

The k-server Problem l k servers in the metric space l l Located at particular points Request of service l l l Happens at the points To serve the request: move a server to the point of request A request sequence , where is a point in M, is a finite sequence of requests 6

The k-server Problem l Two competing algorithms l l l An adversary offline algorithm An online algorithm to be designed The adversary algorithm l l Knows all of right from the beginning and serves them optimally with his own k servers Thus it is offline 7

The k-server Problem l Algorithm to be designed l l l Online Only knows the next request and has to serve it immediately Cost measure l l Total distance moved by all the servers to serve : total cost incurred by the optimal offline algorithm 8

The k-server Problem l l Let denote the cost of algorithm A on request sequence. Definition: A randomized algorithm A is ccompetitive (compared to the optimal offline algorithm), if for all starting configurations there is a real a, independent of , such that 9

Lower Bound of Performance l l l Theorem: For any metric space, the competitive ratio of the k-server problem is at least k (i. e. kcompetitive). Note: This lower bound holds for any randomized algorithm against an optimal online adversary The proof is skipped 10
The Harmonic k-server Algorithm

The Harmonic Algorithm l l Suppose node r makes a request The algorithm works as follows: l l l Let di be the distance from server i to the request node r If any di = 0, do nothing (server i will serve the request; no server moves) Else, use server i with probability inversely proportional to di. . . 12

The Harmonic Algorithm l i. e. let and choose server i with probability . l We denote the Harmonic k-server algorithm by Harmonic or H in the following slides l Eddie Grove proved that H is -competitive for all . 13
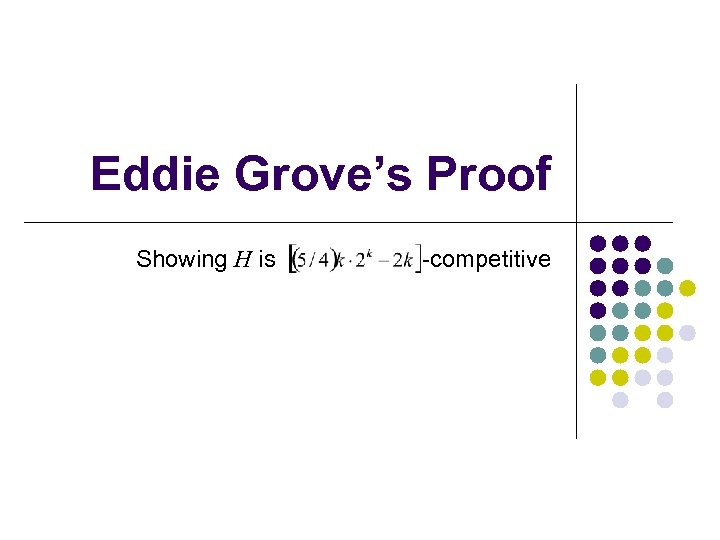
Eddie Grove’s Proof Showing H is -competitive

Process of Serving Requests l l l Let be a request sequence of length m Let be the ith request Think of the process of serving requests as follows: l l For each request , first the adversary moves a server, if necessary, to serve the request Then H “flips a coin” (takes a decision at random according to the pdf mentioned) to choose a server to serve 15

Process of Serving Requests l In this way, we have 2 m phases l l l Odd phase (phase ): adversary serves Even phase (phase 2 i): H serves Let Dj be the distance moved by the server during phase j l l Odd j: Distance moved by adversary’s server Even j: Distance moved by H’s server 16

Introducing the Potential Function l l To analyze, a function is used Define to be the value of at the end of phase t. is chosen in such a fashion that the following three conditions hold: 1. 2. , where ck is the constant to be determined later 3. l Referred as Condition (1), (2) and (3) in the following slides 17

Introducing the Potential Function l What l l l means? From Vijay Gupta’s lecture: represents the amount of work that H can be forced to do if the offline servers do not move My intuition: “Potential energy”, reserved by adversary moves, consumed by H’s moves Why introduce l ? Lemma: If Condition (1), (2) and (3) hold, then H is ck -competitive. 18

Lemma from 3 Conditions l Proof: 19

Lemma from 3 Conditions l Now, (1) (2) 20

Lemma from 3 Conditions l Using Equation (1) and (2), we have Put Also, by the linearity of expectation, we have But, from Condition (1), Hence, 21

More Notations l l l k offline and k online servers Lower-case letter: online server Capital letter: offline server Perfect matchings M between online and offline servers l l Denote by M(x) the mate of x Initial condition: every online server coincides with one offline server l i. e. In the 0 th phase, d(x, M(x)) = 0 for each online server x 22

Matching M l l Each time an online server moves, update matching M Example l l Request placed at offline server A with M(a) = A Online server b, with M(b) = B, moves to the request at A Change matching to: M(b) = A, M(a) = B Matching unchanged for all other servers 23

Active Set l l l Idea of active set is central to the proof Call OFF the set of all k offline servers For and any online server x, the radius of about x is l l AS(x), the active set of x, is the minimizing with largest 24
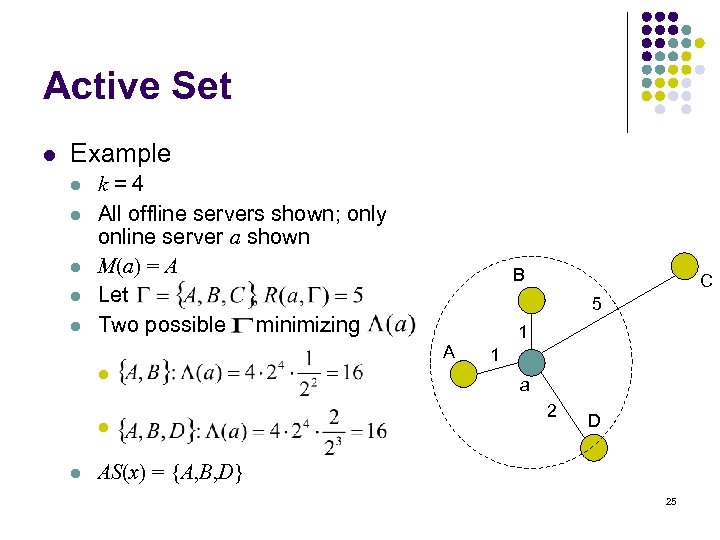
Active Set l Example l l l k=4 All offline servers shown; only online server a shown M(a) = A Let Two possible minimizing B 5 1 A l l l C 1 a 2 D AS(x) = {A, B, D} 25

Active Set l l l Any minimizing set must contain all offline servers within distance of x Intuitively, the active set includes offline servers close to x in comparison to d(x, M(x)) For convenience: l l Definition: 26

The Potential Function All the 3 conditions satisfied?

The Potential Function l Definition: The potential function is computed as: l Condition (1) is satisfied: l l , hence , is always non-negative At t=0, every online server and its matched offline server at identical point, 28

Notes before Analysis l l l Condition (2) corresponds to an adversary move Condition (3) corresponds to a Harmonic move Analyzing an (generic) adversary move and a (generic) Harmonic move completes the proof 29

Notes before Analysis l In the following analysis, a request is placed at some point l l Let A be the offline server moved in response to the request, with M(a)=A Let b be the online server moved in response to the request, with M(b)=B Unless otherwise specified, all expressions describe configuration BEFORE the movement Abuse notation: same variable for a server and the point it occupies 30

Analysis of Adversary Moves l l l Let Z be the place of request A moves a distance D 2 i+1 to Z in phase 2 i+1 Consider the set of servers, l l Physical meaning: online server with A inside its active set, and now A moves out of its active set boundary For won’t increase 31

Analysis of Adversary Moves l Indexing all yh as follows: l l l If a in , y 0=a; else no y 0 For h>0, index yh such that When an offline server moves a distance D 2 i+1 l l increases by at most Other terms do not increase for all 32

Analysis of Adversary Moves l To estimate the increase in potential, we need to estimate S(yh) Let Yh be the offline server matched to yh l Lemma: For h>1, l 33

Analysis of Adversary Moves l Proof: Let . Hence Distance from yh to any Yj in Th is bounded by Hence, 34

Analysis of Adversary Moves l By the minimality in the definition of have , we Hence 35

Analysis of Adversary Moves l The increase in potential due to a move by an offline server of distance D 2 i+1 is at most l Condition (2) is satisfied with competitive ratio 36

Analysis of Harmonic Moves l Three cases l l Case 1: a serves the request at A (i. e. b is identical to a) Case 2: B is close to a, Case 3: B is at distance greater than R(a) from a, We will describe sets NS(x) for which AFTER update matching M l l 37

Harmonic Moves: Case 1 l Case 1: a serves the request at A l AFTER the move, goes to zero Nothing else is changed l Chance is l Expected change in potential l 38

Harmonic Moves: Case 2 l Case 2: B is close to a, l l For , let NS(x)=AS(x). NS(b)={A} Terms for unaffected Potential decreases by at least This term is dropped in an inequality in later proof 39

Harmonic Moves: Case 3 l Case 3: B is at distance greater than R(a) from a, l Call Bi the offline server that is ith closest to a among offline servers at a distance more than R(a) from a l l l Call bi the online server matched to Bi l l Break any ties arbitrarily Let Bl = B bl = b Let dl=d(A, bl) 40

Harmonic Moves: Case 3 l For l l l R(a, NS(a)) will be at most l Now Since l , we have 41

Harmonic Moves: Case 3 l l l Only and changes Expected increase in potential at most The increase happens for each l between 1 and k-S(a) 42

Analysis of Harmonic Moves l It remains to show that satisfies Condition (3) l From previous results, we see that 43

Analysis of Harmonic Moves l The identity, l proves that This completes the proof that the Harmonic algorithm is -competitive for all 44

Reference l l V. Gupta, “CS 497 SHT Spring 1999 Prof. Shang-Hua Teng Lecture 12: 2 nd March, 1999, ” Mar. 1999 E. F. Grove, “The Harmonic online k-server algorithm is competitive, ” Proceedings of the 23 rd Annual ACM Symposium on Theory of Computing, 1991 45
0e4cc010af9393dd0d51d0ba71bf1e9a.ppt