The International Linear Collider Christopher Nantista SLAC SULI

The International Linear Collider Christopher Nantista SLAC SULI Lecture July 22, 2008

Outline • • Introduction Some Accelerator Basics Linear Colliders ILC Anatomy

Introduction

Questions for the Universe • • • Are there undiscovered principles of nature? How can we solve the mystery of dark matter? Are there extra dimensions of space? Do all the forces become one? Why are there so many kinds of particles? What is dark matter? How can we make it in the lab? What are neutrinos telling us? How did the universe come to be? What happened to the antimatter?

Why a Linear Collider? “The international particle physics community has reached concensus that a full understanding of the physics of the Terascale will require a lepton collider in addition to the Large Hadron Collider. ” – Particle Physics Project Prioritization Panel (P 5) Why leptons? Electron-positron (or muon-antimuon) collisions are much cleaner than proton collisions because the former are elementary particles whereas the latter are composed of quarks which share the energy. Clearer results and more accurate measurements can thus be gleaned from lepton annihilations than from hadron collisions. Why linear? Having much smaller mass than protons, electrons radiate more of their energy into synchrotron radiation when bent around a curve. The diameter of a circular electron accelerator must thus be scaled as the energy squared and would be prohibitively large at this energy scale.

An Asside Big e± linear accelerators (linacs) don’t really do much accelerating. * † ‡ Ek (= E – mc 2) ILC main linacs go from here to here 0 1 ke. V (103 e. V) 10 ke. V 100 ke. V 1 Me. V (106 e. V) 10 Me. V 100 Me. V 1 Ge. V (109 e. V) 10 Ge. V 100 Ge. V 1 Te. V (1012 e. V) v/c _ 0 * but they do add energy to the 0. 0625 particles in the beam. 0. 1950 † Proton and ion linacs do more 0. 5482 0. 9411 accelerating due to much larger 0. 9988 rest masses. 0. 999987 ‡ This is good because constant 0. 999999999 speed simplifies accelerator 0. 999999 design. 0. 9999999

Some Accelerator Basics

Microwave Accelerators Charged particles are (generally) accelerated by high oscillating electric fields of electromagnetic waves stored or guided in evacuated metal cavities or structures through which the bunched beam passes. The electromagnetic frequency used is generally in the range of hundreds of megaherz to tens of gigaherz (108– 1011 cycles/s), generally refered to as RF (radiofrequency) or microwaves. MAXWELL’S EQUATIONS: wave equation in free space

Waveguides waveguide – a hollow metal tube for transporting power in confined electromagnetic waves (RF). wave solution: angular frequency: free space wavenumber: cutoff wavenumber*: guide wavenumber: moving waveform free space wavelength A certain amount of transverse cutoff frequency bending/variation of fields is needed to meet boundary conditions at walls of closed waveguide. What’s left of the free space wavenumber (in quadrature) guide goes into longitudinal variation. wavelength Ey of TM 10 mode in rectangular waveguide Ez of TM 01 mode in rectangular waveguide *determined by waveguide cross-section and mode, no wave propagation below fc.

Dispersion Curve w d tan-1 vg w 0 wc e pe s ht lig of tan-1 vp kg k 0 k phase velocity: speed at which wave crests travel group velocity: speed at which power pulse travels Since charged can’t move faster than c, they can’t keep up with the wave crests and thus can’t normally experience sustained net energy gain from a waveguide mode. We need to slow down the confined or guided waves. This is usually done by means of introducing periodicity.

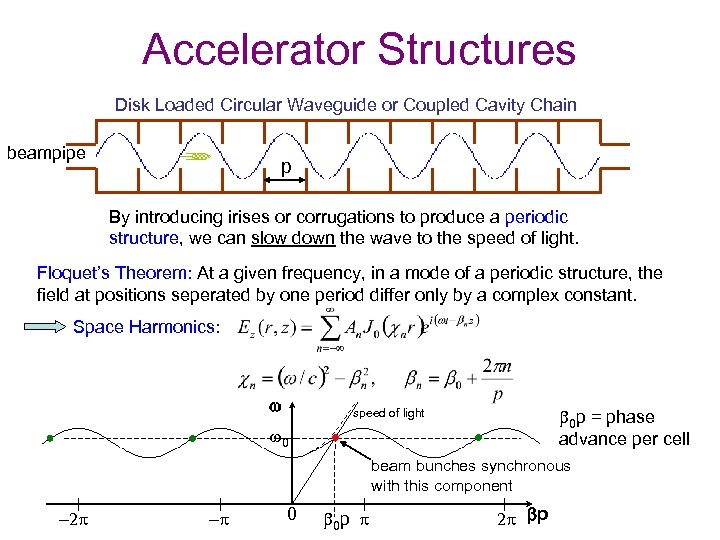Accelerator Structures Disk Loaded Circular Waveguide or Coupled Cavity Chain beampipe p By introducing irises or corrugations to produce a periodic structure, we can slow down the wave to the speed of light. Floquet’s Theorem: At a given frequency, in a mode of a periodic structure, the field at positions seperated by one period differ only by a complex constant. Space Harmonics: w b 0 p = phase advance per cell speed of light w 0 beam bunches synchronous with this component -2 p -p 0 b 0 p p 2 p bp

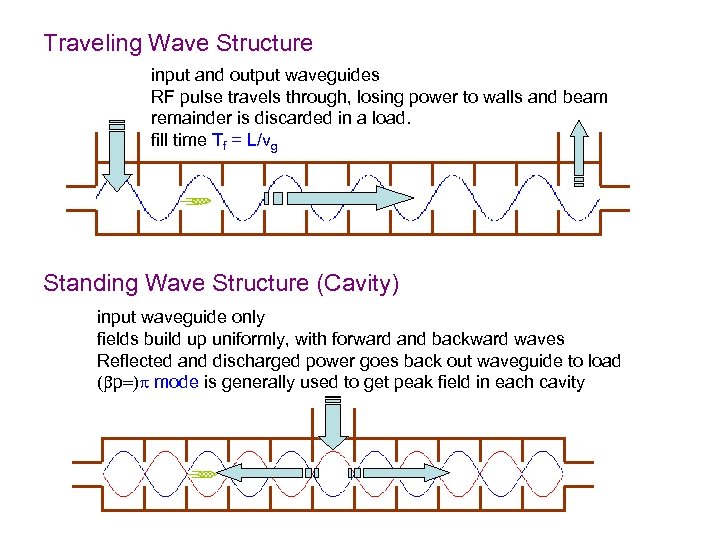Traveling Wave Structure input and output waveguides RF pulse travels through, losing power to walls and beam remainder is discarded in a load. fill time Tf = L/vg Standing Wave Structure (Cavity) input waveguide only fields build up uniformly, with forward and backward waves Reflected and discharged power goes back out waveguide to load (bp=)p mode is generally used to get peak field in each cavity

Structure Parameters (unloaded) quality factor, U=stored energy, Pd = wall dissipated power shunt impedance, V=voltage seen by speed of light beam a geometrical characterization independent of wall losses iris radius normalized to RF free-space wavelength, affects group velocity/cell coupling and wake fields

Traveling Wave phase advance per cell group velocity fill time, time for front of RF pulse to move from input to output. attenuation parameter, wall losses attenuate fields traveling through structure by e-t. Standing Wave characterizes external coupling, Pe is power emitted into waveguide external Q loaded Q cavity time constant

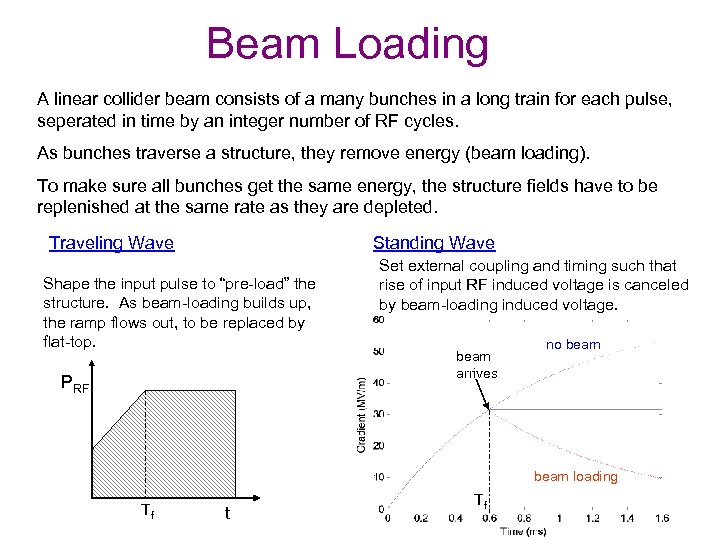Beam Loading A linear collider beam consists of a many bunches in a long train for each pulse, seperated in time by an integer number of RF cycles. As bunches traverse a structure, they remove energy (beam loading). To make sure all bunches get the same energy, the structure fields have to be replenished at the same rate as they are depleted. Traveling Wave Standing Wave Shape the input pulse to “pre-load” the structure. As beam-loading builds up, the ramp flows out, to be replaced by flat-top. PRF Set external coupling and timing such that rise of input RF induced voltage is canceled by beam-loading induced voltage. beam arrives no beam loading Tf t Tf

Wake Fields Bunches of charged particles traversing a cavity/structure, in addition to taking energy from the fundamental accelerating mode, leave energy behind in other RF field modes called higher order modes or HOM’s. These fields give kicks to following bunches, and their buildup and affect must be controlled by: • Damping – lets the power from these modes flow out to absorbing loads through waveguides or couplers which don’t couple to the accelerating mode. • Detuning – subtly varying the dimensions of the cells so that HOM frequencies are different from cell to cell. The bunches then experience them at various phases, which tends to cancel their cumulative affect.

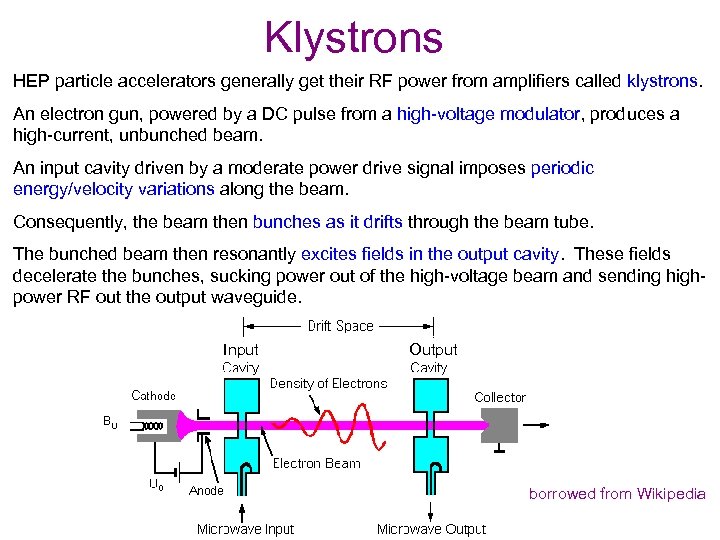Klystrons HEP particle accelerators generally get their RF power from amplifiers called klystrons. An electron gun, powered by a DC pulse from a high-voltage modulator, produces a high-current, unbunched beam. An input cavity driven by a moderate power drive signal imposes periodic energy/velocity variations along the beam. Consequently, the beam then bunches as it drifts through the beam tube. The bunched beam then resonantly excites fields in the output cavity. These fields decelerate the bunches, sucking power out of the high-voltage beam and sending highpower RF out the output waveguide. Input Output borrowed from Wikipedia

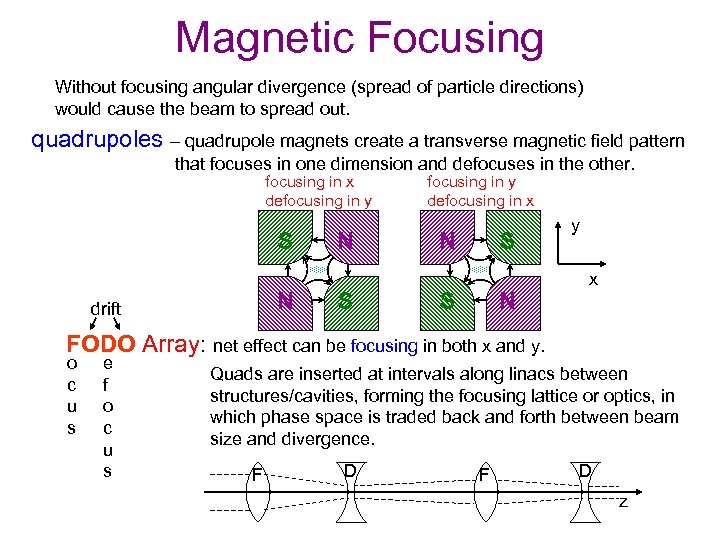Magnetic Focusing Without focusing angular divergence (spread of particle directions) would cause the beam to spread out. quadrupoles – quadrupole magnets create a transverse magnetic field pattern that focuses in one dimension and defocuses in the other. focusing in x defocusing in y S N drift N S focusing in y defocusing in x N S S N y x FODO Array: net effect can be focusing in both x and y. o c u s e f o c u s Quads are inserted at intervals along linacs between structures/cavities, forming the focusing lattice or optics, in which phase space is traded back and forth between beam size and divergence. F D z

Emittance An important beam parameter, emittance (e) is the area of the particle distribution in phase space. x’ = dx/dz x’ angular divergence focus drift x’ x At upright points in lattice: area conserved x (bi-Gaussian distribution) Same for y phase space. For longitudinal emittance, sz = bunch length and DE replaces divergence. Damping rings reduce the emittances to minimum values. Growth through the rest of the machine must then be carefully controlled.

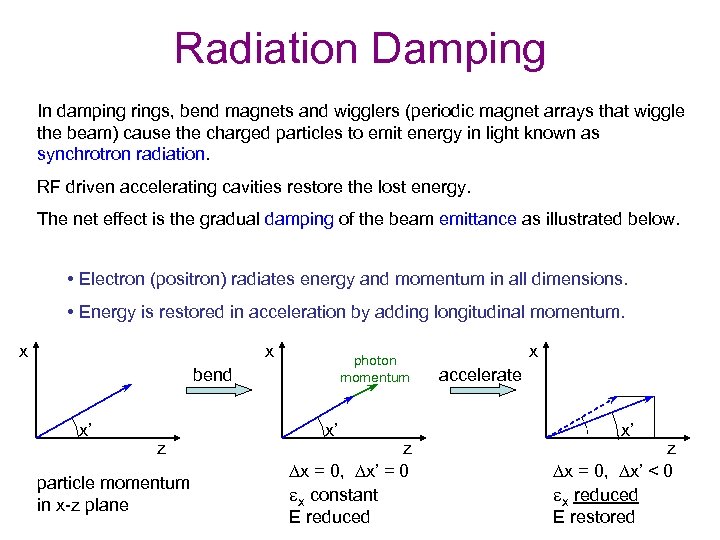Radiation Damping In damping rings, bend magnets and wigglers (periodic magnet arrays that wiggle the beam) cause the charged particles to emit energy in light known as synchrotron radiation. RF driven accelerating cavities restore the lost energy. The net effect is the gradual damping of the beam emittance as illustrated below. • Electron (positron) radiates energy and momentum in all dimensions. • Energy is restored in acceleration by adding longitudinal momentum. x x photon momentum bend x’ z particle momentum in x-z plane x’ z Dx = 0, Dx’ = 0 ex constant E reduced x accelerate x’ z Dx = 0, Dx’ < 0 ex reduced E restored

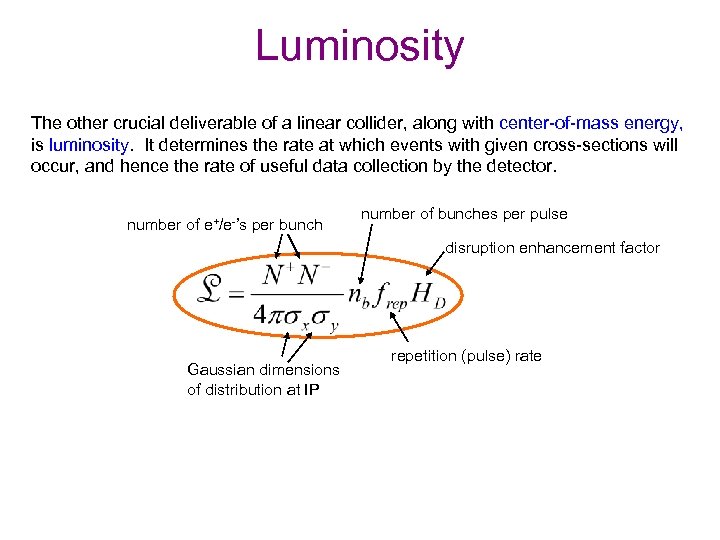Luminosity The other crucial deliverable of a linear collider, along with center-of-mass energy, is luminosity. It determines the rate at which events with given cross-sections will occur, and hence the rate of useful data collection by the detector. number of e+/e-’s per bunch number of bunches per pulse disruption enhancement factor Gaussian dimensions of distribution at IP repetition (pulse) rate

Linear Colliders

Parts of a Linear Collider • Electron Gun – produces beam electrons • Injector – pre-accelerates and shapes beam (e. g. collimation, bunch compression) • Positron production – uses electron beam to produce positrons (undulator, target) • Damping rings – reduce emmitance of beams • Main linacs – accelerate up to desired collision energy while preserving emittance • Final focus – collimate and focus beams for smallest cross-sections at IP • Interaction Point (IP) – collide beams, surrounded by detector • Dump – discard spent beams, absorbing enormous energy Detector: massive, multi-layered high-tech instrument surrounding IP that senses and tracks particles coming from collisions using various technologies, identifies interesting events, and stores data for later analysis. Requiring different expertise outside “accelerator physics”, it is usually treated as separate from the collider, developed in parallel, and given its own name. Which is more important? Obviously the linear collider and the detector have a symbiotic relationship in which either one is useless without the other.

Linear Collider History (A) SLC (Stanford Linear Collider) 1 st and only (so far) linear collider • began construction in 1983, operated from 1989 -1998. • Used upgraded SLAC 2 -mile linac • e-’s & e+’s share linac, bent through separate arcs for collision • single bunch, NC TW structures, S -band (2. 856 GHz) • Cof. M energy ~90 -100 Ge. V • Polarized source added in 1992 • Allowed detailed studies of Z 0 particle (a carrier boson of the weak force)

Linear Collider History (B) The Competition (1985? - 2004) TESLA (Te. V Energy Superconducting Linear Accelerator) – DESY (Germany)based, superconducting SW cavities, L-band (1. 3 GHz) S-Band – most straightforward extension of 2. 856 GHz SLC technology to larger machine C-band – KEK alternate approach, innovative 5. 712 GHz choke-mode cells. NLC (Next Linear Collider) – SLAC-based X-band (11. 424 GHz), NC TW, promises higher gradient, required development of RF pulse compression, and wakefield damping/detuning, Fermilab increasingly involved JLC (Japan Linear Collider) – KEK-centered X-band design, collaborative R&D with NLC, later redubbed GLC (Global Linear Collider) for greater pan-Asian participation. VLEPP – Russian Ku-band (14 GHz) design. CLIC (Compact Linear Collider) – CERN (Europe)-based, 30 GHz NC TW, two-beam approach with higher energy reach.

Linear Collider History (C) A United Front Beyond a certain point, it is not sustainable, in terms of funding and manpower, to continue to pursue multiple designs. The physics community agreed to let an international group of distinguished, unbiased experts referee a shoot-out between the leading contenders for linear collider technology: TESLA L-Band Superconducting SW Cavities NLC/GLC X-Band Copper TW Structures After visiting the labs to assess R&D status and considering multiple factors: August 19, 2004: ITRP (International Technology Recommendation Panel) recommends superconducting technology for a 0. 5 -1 Te. V linear collider: “…both technologies can achieve the goals presented in the charge. Each had considerable strengths. ” “…recommending a technology, not a design. ”

ILC (International Linear Collider) program is born. The accelerator community accepts and rallies behind decision. SLAC wraps up X-band development, rapidly adjusts and gets on board to play a leading role in the design of a cold (superconducting) L-band machine. Why International? : Cost of project would require more resources than one country could afford. 3 Regions: Americas, Europe, Asia GDE (Global Design Effort): International team of >60 experts leading the effort and steering the coordinated R&D program, headed by Barry Barish of Cal Tech, with a leader for each of the three regions. August, 2007: RDR (Reference Design Report) published, baseline design. ILC is currently in the TDP (Technical Design Phase): reduce cost, optimize design, prove technology

ILC Anatomy

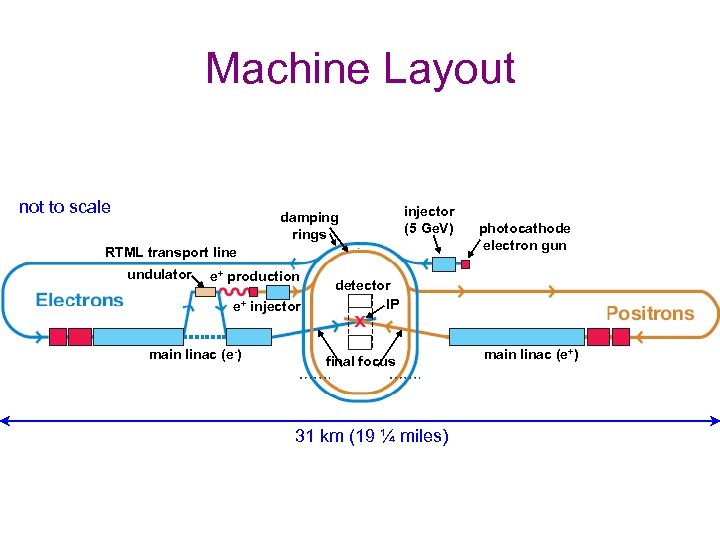Machine Layout not to scale damping rings injector (5 Ge. V) RTML transport line undulator e+ production e+ injector main linac (e-) photocathode electron gun detector IP final focus 31 km (19 ¼ miles) main linac (e+)

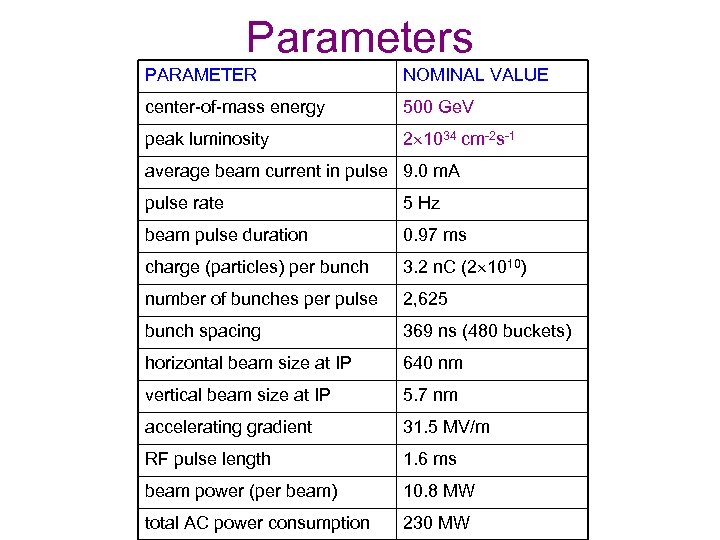Parameters PARAMETER NOMINAL VALUE center-of-mass energy 500 Ge. V peak luminosity 2 1034 cm-2 s-1 average beam current in pulse 9. 0 m. A pulse rate 5 Hz beam pulse duration 0. 97 ms charge (particles) per bunch 3. 2 n. C (2 1010) number of bunches per pulse 2, 625 bunch spacing 369 ns (480 buckets) horizontal beam size at IP 640 nm vertical beam size at IP 5. 7 nm accelerating gradient 31. 5 MV/m RF pulse length 1. 6 ms beam power (per beam) 10. 8 MW total AC power consumption 230 MW

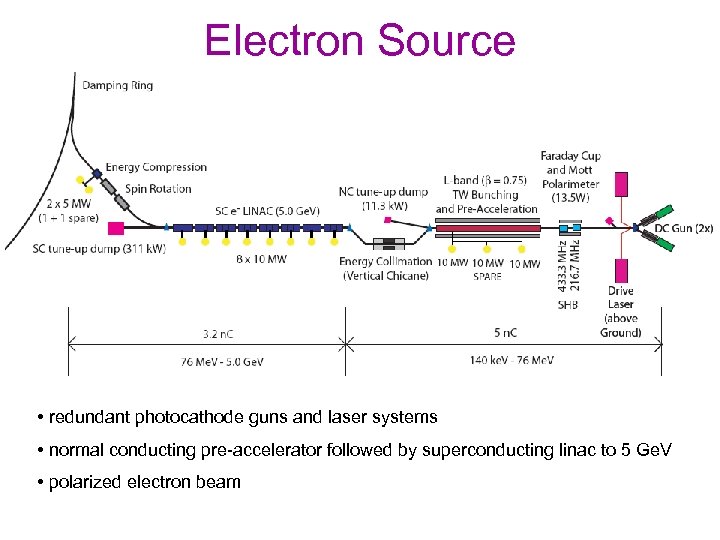Electron Source • redundant photocathode guns and laser systems • normal conducting pre-accelerator followed by superconducting linac to 5 Ge. V • polarized electron beam

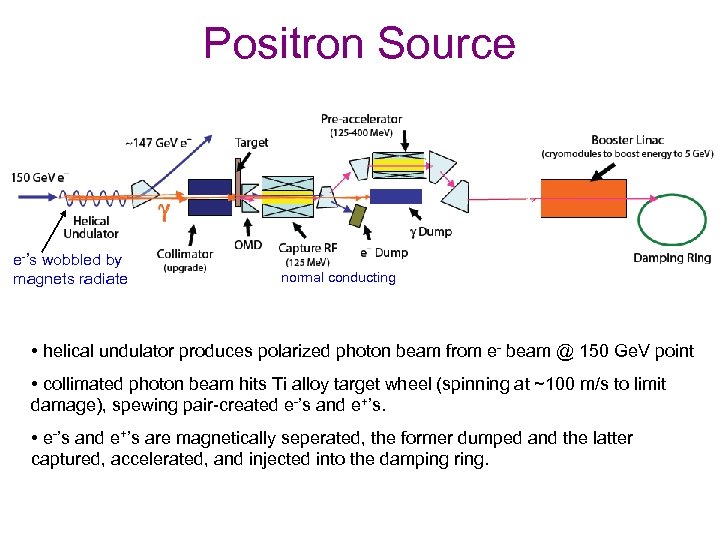Positron Source e-’s wobbled by magnets radiate normal conducting • helical undulator produces polarized photon beam from e- beam @ 150 Ge. V point • collimated photon beam hits Ti alloy target wheel (spinning at ~100 m/s to limit damage), spewing pair-created e-’s and e+’s. • e-’s and e+’s are magnetically seperated, the former dumped and the latter captured, accelerated, and injected into the damping ring.

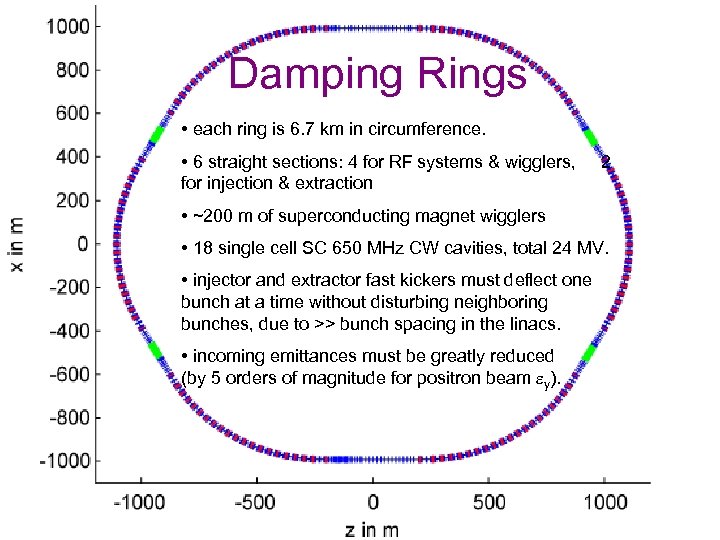Damping Rings • each ring is 6. 7 km in circumference. • 6 straight sections: 4 for RF systems & wigglers, for injection & extraction 2 • ~200 m of superconducting magnet wigglers • 18 single cell SC 650 MHz CW cavities, total 24 MV. • injector and extractor fast kickers must deflect one bunch at a time without disturbing neighboring bunches, due to >> bunch spacing in the linacs. • incoming emittances must be greatly reduced (by 5 orders of magnitude for positron beam ey).

Superconducting RF Certain materials, at temperatures close to absolute zero, enter a superconducting state in which surface resistivity vanishes, although for RF a slight residual resistivity remains. For accelerators, SC cavities provide an efficient way to build up and store accelerating fields no RF pulse compression, long beam pulses. Cryogenics systems (using liquid He) and well insulated cryomodules are required to maintain cavities at operating temperature. Accelerating gradient has a hard limit set by the maximum sustainable (in the SC state) surface magnetic field. Material purity and surface preparation also affect achievable gradient.

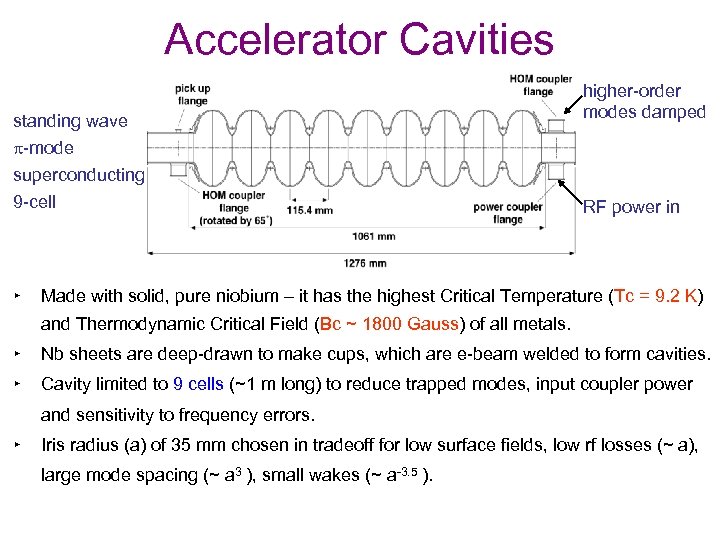Accelerator Cavities standing wave higher-order modes damped p-mode superconducting 9 -cell ‣ RF power in Made with solid, pure niobium – it has the highest Critical Temperature (Tc = 9. 2 K) and Thermodynamic Critical Field (Bc ~ 1800 Gauss) of all metals. ‣ Nb sheets are deep-drawn to make cups, which are e-beam welded to form cavities. ‣ Cavity limited to 9 cells (~1 m long) to reduce trapped modes, input coupler power and sensitivity to frequency errors. ‣ Iris radius (a) of 35 mm chosen in tradeoff for low surface fields, low rf losses (~ a), large mode spacing (~ a 3 ), small wakes (~ a-3. 5 ).

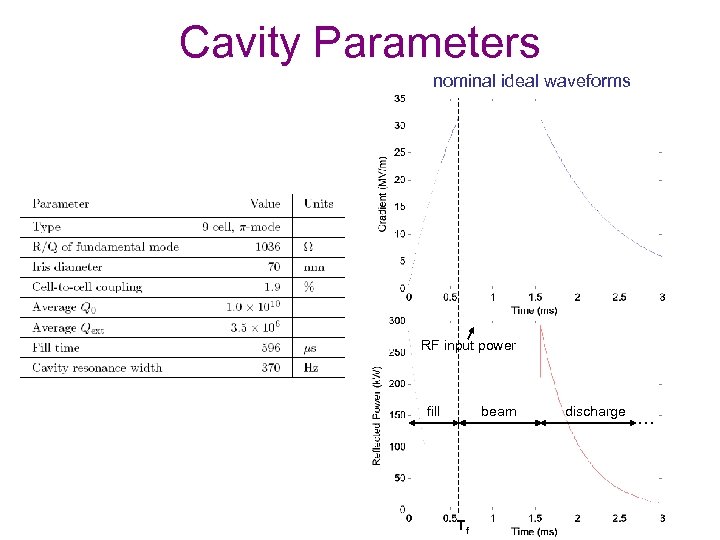Cavity Parameters nominal ideal waveforms RF input power fill beam Tf discharge …

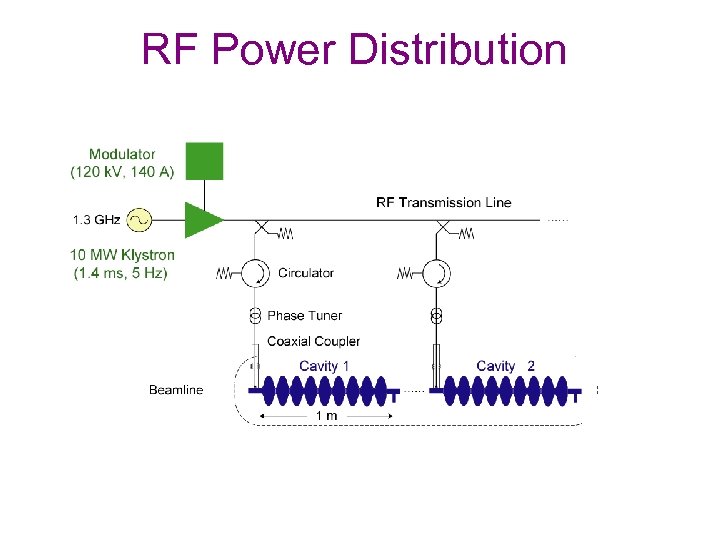RF Power Distribution

Cryomodules 8 or 9 cavities per cryomodule SC quads in center of every 3 rd one

Klystrons BASELINE: 10 MW multi-beam klystrons* (MBK’s) with ~65% efficiency Being developed by three tube companies in collaboration with DESY. Thales CPI Toshiba *operate at lower voltage yet with a higher efficiency than simpler single round beam klystrons.

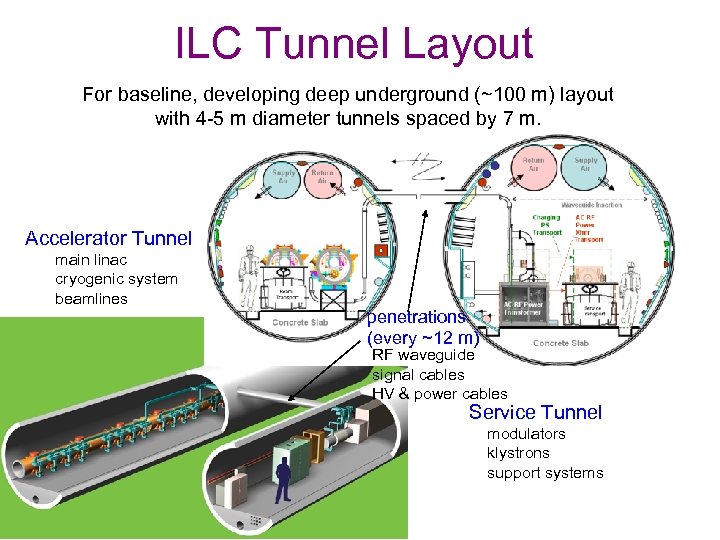ILC Tunnel Layout For baseline, developing deep underground (~100 m) layout with 4 -5 m diameter tunnels spaced by 7 m. Accelerator Tunnel main linac cryogenic system beamlines penetrations (every ~12 m) RF waveguide signal cables HV & power cables Service Tunnel modulators klystrons support systems

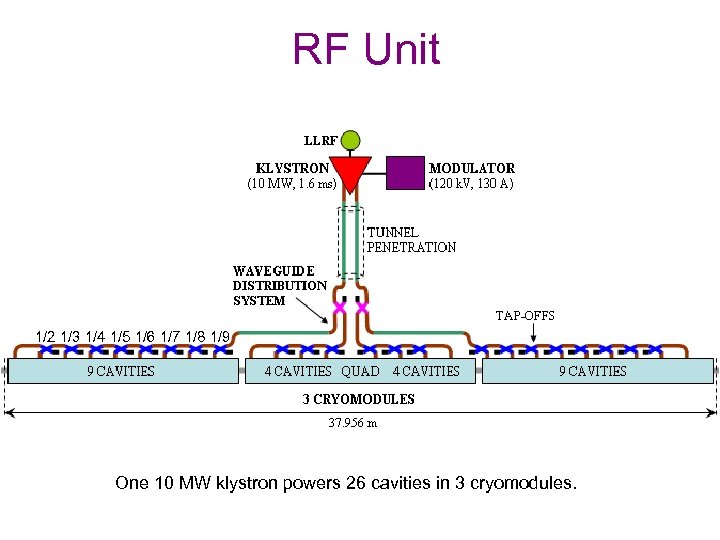RF Unit 1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9 One 10 MW klystron powers 26 cavities in 3 cryomodules.

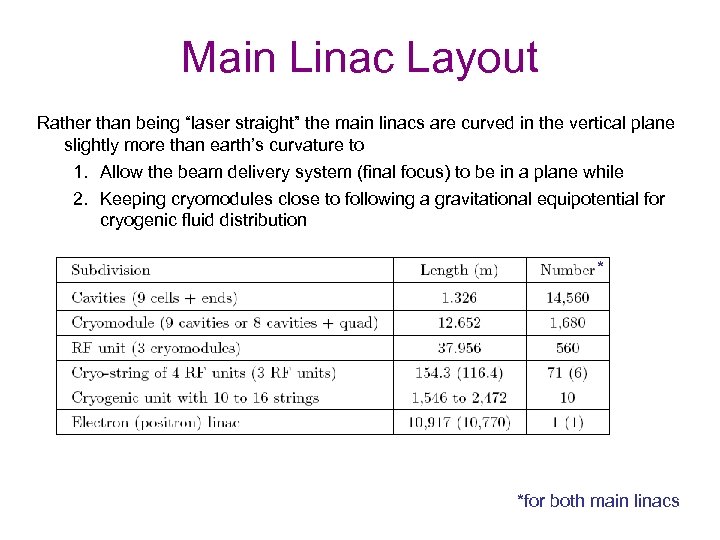Main Linac Layout Rather than being “laser straight” the main linacs are curved in the vertical plane slightly more than earth’s curvature to 1. Allow the beam delivery system (final focus) to be in a plane while 2. Keeping cryomodules close to following a gravitational equipotential for cryogenic fluid distribution * *for both main linacs

Conclusion The ILC is an ambitious project, of which I’ve attempted to paint a general outline along with some accelerator physics background and history. Many challenges remain, including: • improving the cavity fabrication to increase the yield of units that reach gradient spec. • producing a robust klystron • demonstrating the damping ring design concept • improving expected availability (fraction of time all systems go) • REDUCING COST Politically/financially, the ILC has taken a hit recently in the UK and the US, but the collaboration infrastructure remains in place, and we hope for increased R&D support. Real momentum may have to await signals from the LHC that the energy reach of this machine is indeed rich in physics.