Скачать презентацию The Future of Graph Drawing and a rhapsody
7924e73fee89e60a4d6373afff13547a.ppt
- Количество слайдов: 111
The Future of Graph Drawing and a rhapsody Peter Eades 1
Question: What is the future of Graph Drawing? Answer: . . . I’ll tell you later. . . But first: some constraints, and a brief history. . 2
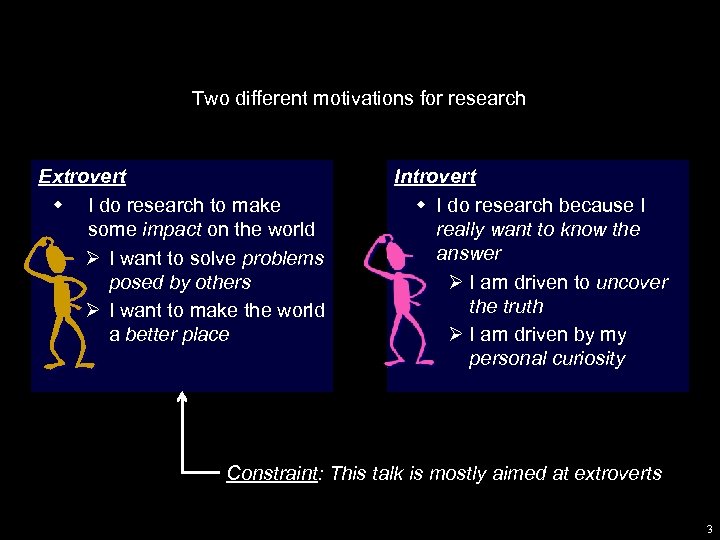Two different motivations for research Extrovert w I do research to make some impact on the world Ø I want to solve problems posed by others Ø I want to make the world a better place Introvert w I do research because I really want to know the answer Ø I am driven to uncover the truth Ø I am driven by my personal curiosity Constraint: This talk is mostly aimed at extroverts 3
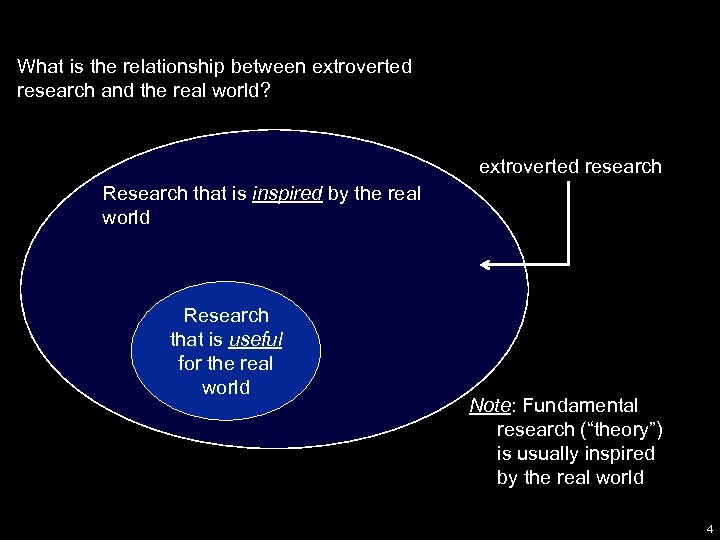What is the relationship between extroverted research and the real world? extroverted research Research that is inspired by the real world Research that is useful for the real world Note: Fundamental research (“theory”) is usually inspired by the real world 4
A brief history 5
1970 s An idea emerges: w Visualise graphs using a computer! w Inspired by the need for better human decision making w Implementations aimed at business decision making, circuit schematics, software diagrams, organisation charts, network protocols, and graph theory Some key ideas defined w Aesthetic criteria defined (intuitively) w Key scientific challenge defined: layout to optimise aesthetic criteria 6
1980 s Exciting algorithms and geometry: w Many fundamental graph layout algorithms designed, enunciated, implemented, and analysed w Extra inspirational ideas from graph theory, geometry, and algorithmics w Planarity becomes a central concept 7
1990 s Maturity w Graph Drawing matures as a discipline w The Graph Drawing Conference begins w The academic Graph Drawing “community” emerges More demand w High data volumes increase demand for visualization w Small companies appear More communities w Information Visualization discipline appears 8
2000 s Even more demand w Data volumes become higher than ever imagined, and demand for visualization increases accordingly w New customers: systems biology, social networks, security, . . . Better engineering w More usable products, both free and commercial w More companies started, older companies become stable Invisibility w Graph drawing algorithms become invisible in vertical tool 9
Question: What is the future of Graph Drawing? Answer: . . . I’ll tell you later. . . But first: Ø A rhapsody: unsupported conjectures, subjective observations, outlandish claims, a few plain lies, and some open problems 10
Subjective Observation: Graph Drawing is successful 11
Graph Drawing is successful • Algorithms for graph drawing are used in many industries: Ø Biotechnology Ø Software engineering Ø Networks Ø Business intelligence Ø Security • Graph drawing software is an industry: Ø Employs about 500 FTE people Ø Market worth up to $100, 000 per year Ø About 100 FTE researchers • Graph Drawing is scientifically significant Ø Graph Drawing has provided an elegant algorithmic approach to the centuries-old interplay between combinatorial and geometric structures Ø GD 2010 is a “rank A” conference Ø Graph drawing papers appear in many top journals and conference proceedings 12
“Graph Drawing is the big success story in information visualization” Stephen North, September 2010 13
Subjective Observation: Graph Drawing is connected to many other disciplines 14
Keith Nesbitt 2003: use metro map metaphor for abstract data connections many applications large ABSTRACT DATA Abstract Data multiattributed finding automated intelligent tools VIRTUAL ENVIRONMENT human S new user-interface perceptual tools technology many interaction styles INFORMATION DISPLAY increase humancomputer bandwidth virtual real worlds SOFTWARE CASE ENGINEERING STUDY abstraction architectur e taxonomy iterative prototyping finding trading rules visual data mining vision information visualisation quality principles MS-Taxonomy MS-Guidelines sensory bias sensory interaction Human Perception MS-Process Software Engineering Case Study - Stock Market hearing haptics information sonification information haptisation spatial metaphors virtual abstract worlds temporal metaphors guidelines for information perceptualisation display stock market data guidelines for MS-Taxonomy structure MS-TAXONOMY VE platforms task analysis process structure data characterisation display mapping guidelines for temporal metaphors mapping spatial direct temporal metaphors summative evaluation MS-GUIDELINES consider hardware platform consider software platform guidelines for perception guidelines for spatial for direct metaphors design guidelines informatio n metaphors direct metaphors virtual hybrid worlds technical analysis design process MSPROCESS physiology perceptual data mining Data Mining cognition patterns DATA MINING Virtual Environments Information Display HUMAN PERCEPTION formative evaluation i-CONE Barco Baron Responsive Workbench Haptic Workbench WEDGE prototyping expert heuristic evaluation 3 D bar chart moving average surface bid. Ask landscape haptic 3 D bar chart haptic moving average surface auditory bid. Ask landscape 15
Info Vis Computer Graphics Data. Mining Graph. Drawing HCI Algorithms Computational Geometry Computer Science Visual. Languages Graph Drawing: Connections Combinatorial. Geometry Graph. Theory Graphic Art Linear. Algebra 16
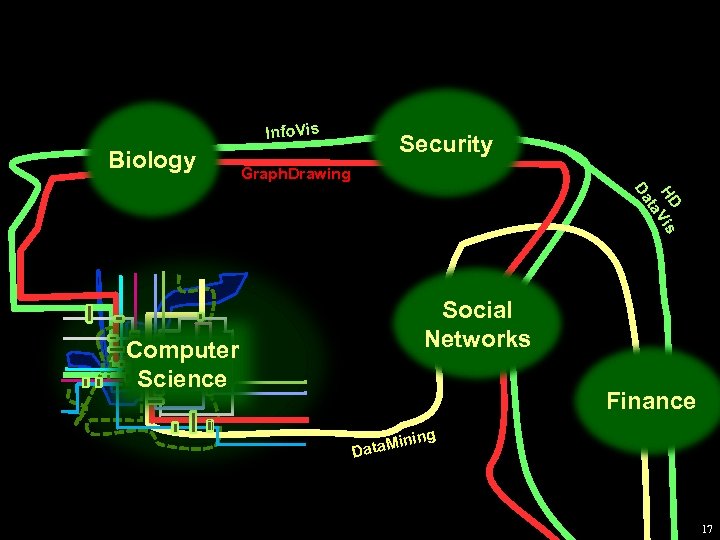Info. Vis Biology Security Graph. Drawing HD Vis ta Da Social Networks Computer Science Finance Data. M ining 17
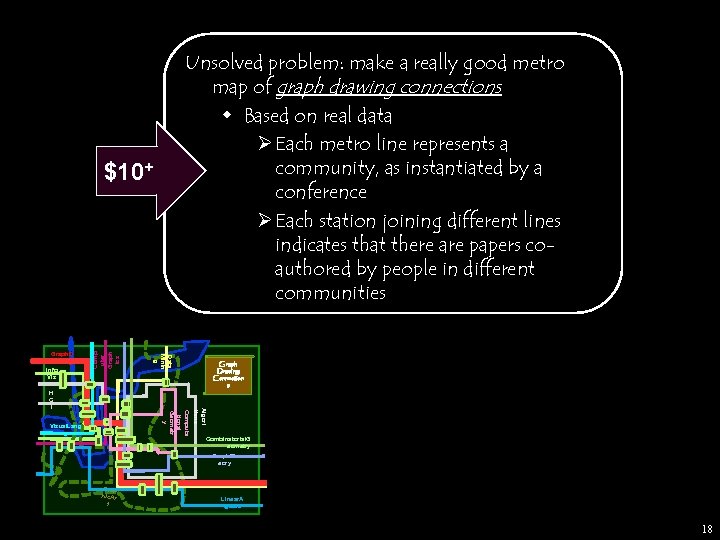Unsolved problem: make a really good metro map of graph drawing connections w Based on real data Ø Each metro line represents a community, as instantiated by a conference Ø Each station joining different lines indicates that there are papers coauthored by people in different communities Visual. Lang uages Graph Drawing: Connection s Algori thms Computa tional Geometr y H C I Data Minin g Graph. D rawing Info Vis Comp uter Graph ics $10+ Combinatorial. G eometry Graph. Th eory Grap hic. Ar t Linear. A lgebra 18
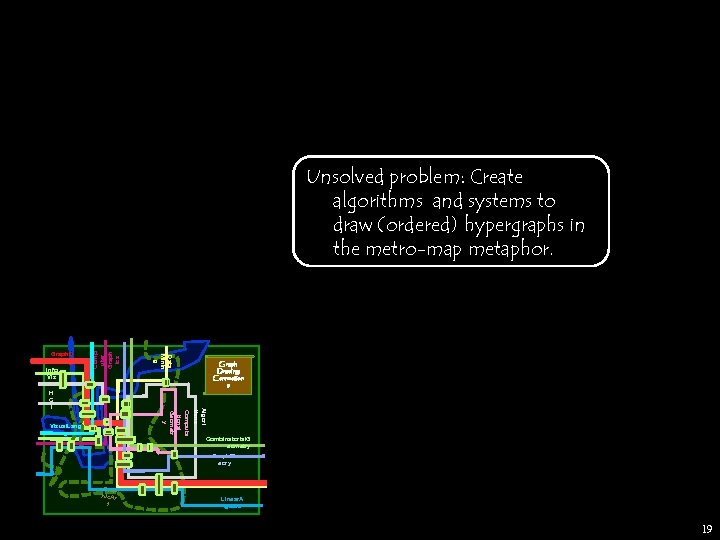Visual. Lang uages Graph Drawing: Connection s Algori thms Computa tional Geometr y H C I Data Minin g Graph. D rawing Info Vis Comp uter Graph ics Unsolved problem: Create algorithms and systems to draw (ordered) hypergraphs in the metro-map metaphor. Combinatorial. G eometry Graph. Th eory Grap hic. Ar t Linear. A lgebra 19
Outlandish claim: Graph Drawing is dying 20
Interview with a Very Experienced Industry Researcher in a Telco, Sept 14, 2010 Interviewer: “What are the most useful results from the Graph Drawing researchers in the last ten years? ” Industry Researcher:
Interview with a Very Experienced Industry Researcher in a Telco, Sept 14, 2010 Interviewer: “Any other useful results from the Graph Drawing researchers in the last ten years? ” Industry Researcher:
Interview with the CEO and CTO of a Graph Drawing software company, Sept 15, 2010 Interviewer: “What are the most useful results from the Graph Drawing researchers in the last ten years? ” CTO: “Fast force directed methods. When was that? ” Interviewer: “Around GD 2000, I think. . . Almost 10 years ago. ” CTO: “Yes. We implemented some of them. We had to fix them a bit, but they gave us much better runtimes. ” Interviewer: “Any other useful results from the Graph Drawing researchers in the last ten years? ” Industry people:
Interview with the CEO and CTO of a Graph Drawing software company, Sept 15, 2010 CEO: “Well, our tools are much better engineered than “ten years ago. We’ve spent a lot of energy. . . ” Interviewer:
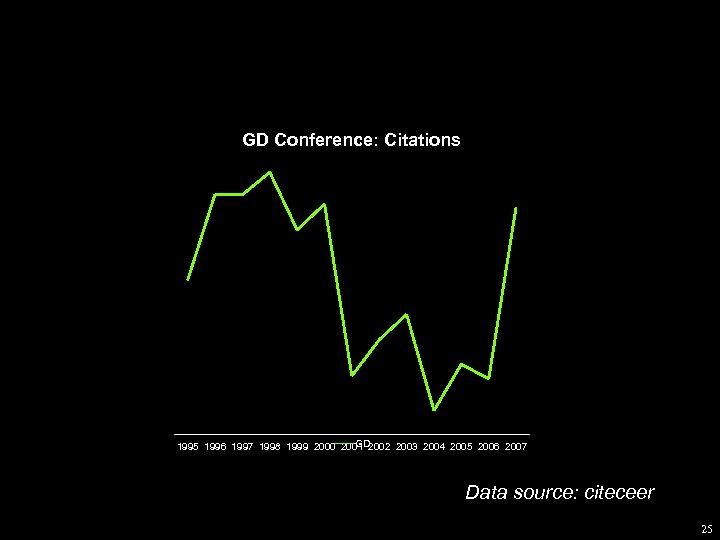GD Conference: Citations GD 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 Data source: citeceer 25
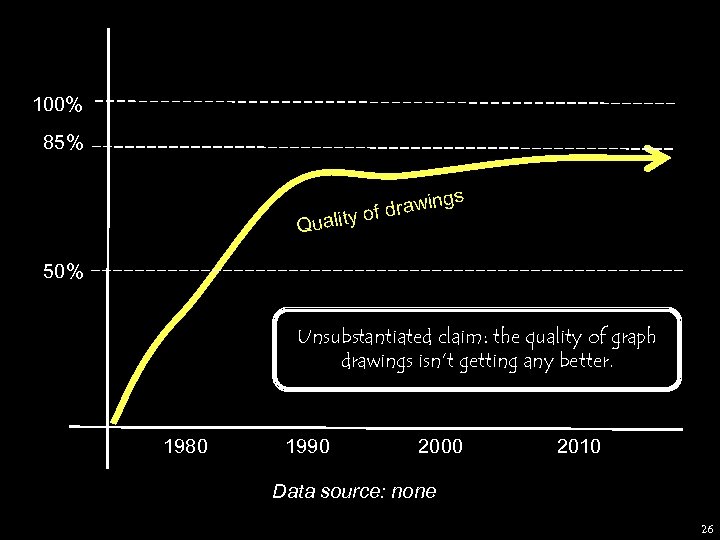100% 85% s ing f draw lity o Qua 50% Unsubstantiated claim: the quality of graph drawings isn’t getting any better. 1980 1990 2000 2010 Data source: none 26
Open Problem: Is it worth the money? 27
Average cost of Graph Drawing Researcher per year (assuming $100 Kpa, 2. 5 oncost multiplier) = $250 K. There are probably about 100 FTE GD researchers in the world. Ø The cost of the past ten years of Graph Drawing Research is about $25 M $250 M Open Problem: Has the world made a profit from this $25 M investment yet? If not, how long will it take to get some ROI? 28
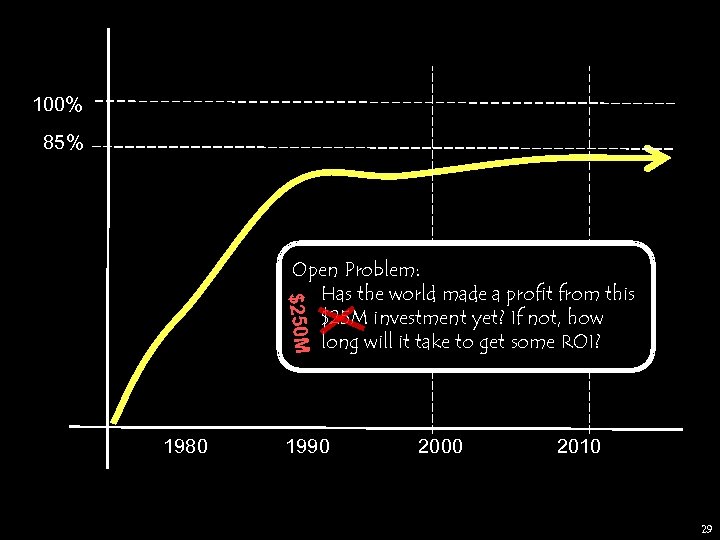100% 85% $250 M Open Problem: Has the world made a profit from this $25 M investment yet? If not, how long will it take to get some ROI? 1980 1990 2000 2010 29
Open Problem: What kind of community is GD? 30
The GD community • Every node is a paper at the GD conference • Edge from A to B if A cites B 31
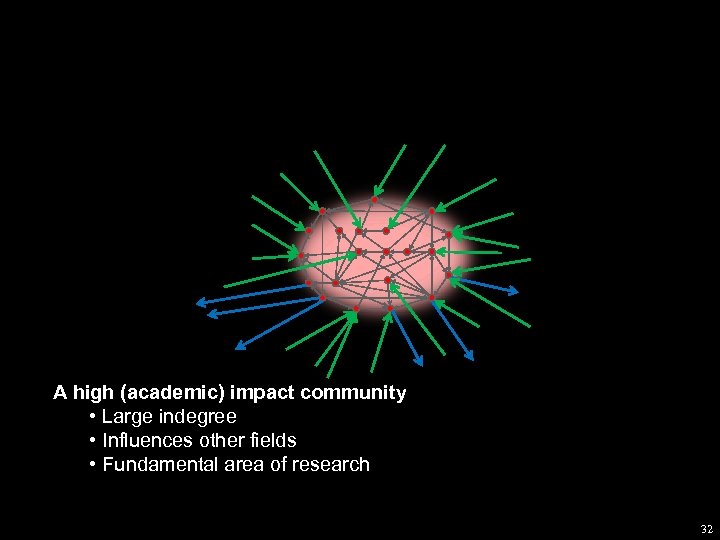A high (academic) impact community • Large indegree • Influences other fields • Fundamental area of research 32
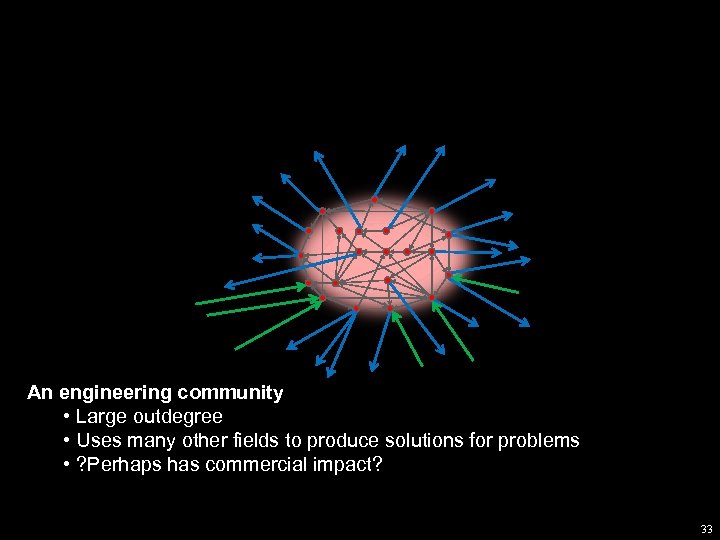An engineering community • Large outdegree • Uses many other fields to produce solutions for problems • ? Perhaps has commercial impact? 33
An island community • Not much connection to the outside • ? Perhaps has no impact? • ? Introspective community? 34
Unsolved problem Open Problem: Ø What kind of community is GD? Ø Has its character changed over time? $10+ Ø Can you show this in a picture (or a time-lapse animation) of citation network(s)? 35
Unsupported conjecture: Planarity has about 5 years to either live or die 36
1930 s: Fary Theorem w Straight-line drawings exist 1960 s: Tutte’s algorithm w A straight-line drawing algorithm 1970 s: Read’s algorithm w Linear time straight-line drawing 1984: Tamassia algorithm Ø Minimum number of bends 1987: Tamassia-Tollis algorithms w Visibility drawing, upward planarity 1989: de Frassieux - Pach - Pollack Theorem w Quadratic area straight-line drawing 37
Conversation at GD 1994, between an academic delegate and a industry delegate Industry delegate: “Why are you guys so obsessed with planarity? Most graphs that I want to draw aren’t planar. ” Academic delegate: “Well, planarity is a central concept even for non-planar graphs. To be able to draw general graphs, we find a topology with a small number of edge crossings, model this topology as a planar graph, and draw that planar graph. ” Industry delegate: “Sounds good. But I don’t know how to solve these sub-problems, for example, how to find a topology with a small number of crossings” Academic delegate: “These problems are fairly difficult and we don’t have perfect solutions. But we expect a few more years of research and we will get good results” Industry delegate:
Mid 1990 s: Mutzel’s thesis w Crossing reduction by integer linear programming 1995: Purchase experiments w Crossings really do inhibit understanding Late 1990 s: w Many beautiful papers on drawing planar graphs w Good crossing reduction methods Early 2000 s: Ø Many more beautiful papers on drawing planar ue tr graphs st o. . lm A. . . Subjective Observation: Plain lie: The graph drawing community is GD 2010: More than 60% of obsessed with planarity. papers are about planar graphs 39
Interview with the CEO and CIO of a Graph Visualization company, Sept 15 2010 Interviewer: “Do you use planar graph drawing algorithms? ” CEO: “No. ” Interviewer: “Why not? ” CEO: “Too much white space. Stability is a problem. Too difficult to integrate constraints. Incremental planar drawing doesn’t work well. ” CIO:
Interview with a Very Senior Software Engineer in a Very Large Company that has a Very Small Section that produces visualization software, Sept 23 2010 Interviewer: “Do your graph visualization tools use planar graph drawing algorithms? ” Software Engineer: “Our customers want hierarchical layout first, and hierarchical layout second, and then they want hierarchical layout. We also have spring algorithms, but I’m not sure whether they use them. ” Interviewer: “Yes, but maybe deep down in your software there is a planarity algorithm, or maybe a planar graph drawing algorithm? ” Software Engineer: “No. No planarity. ” Note: Yworks does use planar graph drawing algorithms 41
Outlandish claim: Planarity-based methods are valuable, but need more time to prove themselves. Unsupported conjecture: Around 2015, either: Ø Yworks wins a much larger market share, based on the competitive advantage of planarity-based methods, or Ø Yworks finds that planarity-based methods are not useful, and drops the idea. Subjective observation: To know whether planar graph drawing is worthwhile: Ø We need to do lots more empirical work. Ø We probably don’t need many more theorems. 42
Outlandish Claim: The graph drawing community can contribute a lot to solving the scale problem 43
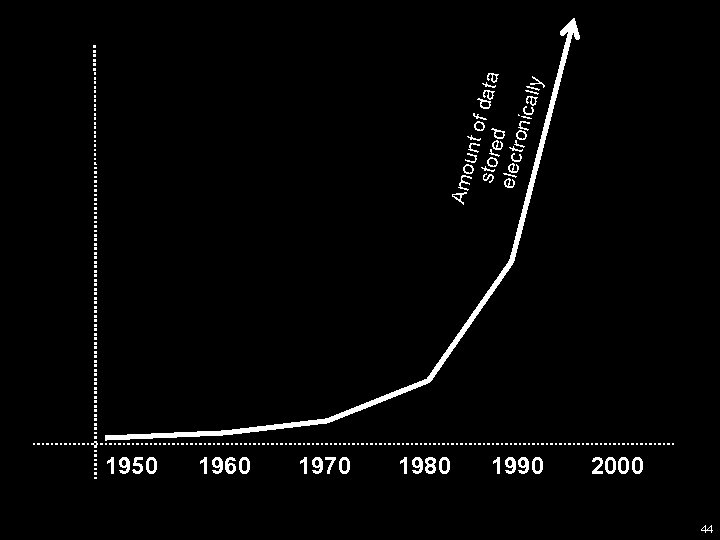1950 1960 1970 1980 1990 2000 44 Amo unt o store f data elect d ronic ally
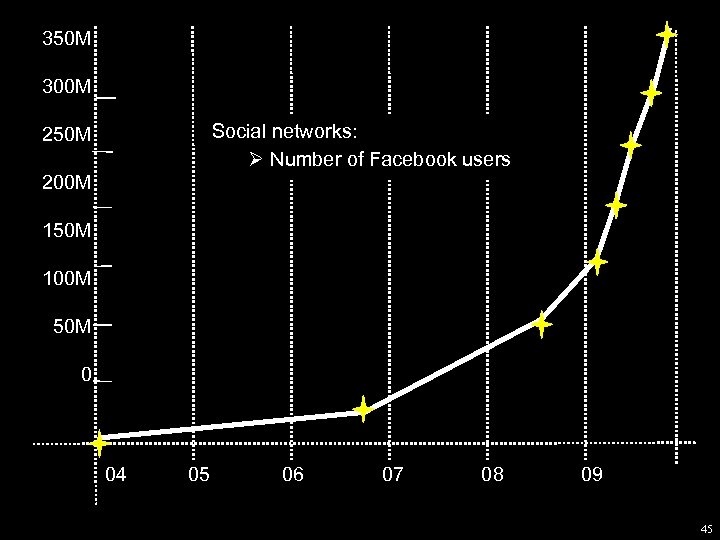350 M 300 M Social networks: Ø Number of Facebook users 250 M 200 M 150 M 100 M 50 M 0 04 05 06 07 08 09 45
The scale problem currently drives much of Computer Science • Data sets are growing at a faster rate than the human ability to understand them. • Businesses (and sciences) believe that their data sets contains useful information, and they want to get some business (or scientific) value out of these data sets. 46
For Graph Drawing, there are two facets of the scale problem: 1. Computational complexity w Efficiency w Runtime Ø We need more efficient algorithms 2. Visual complexity w Effectiveness w Readability Ø We need better ways to untangle large graphs 47
Graph Drawing has proposed three approaches to the scale problem: 1. Use 3 D: spread the data over a third dimension 2. Use interaction: spread the data over time 3. Use clustering: view an abstraction of the data 48
Well supported claim: 3 D is almost dead 49
Conversation between an Australian academic and a Canadian IBM research manager, 1992 IBM Research Manager: “Graphics cards capable of fast 3 D rendering will soon become commodity items. They will give an unprecedented ability to draw diagrams in 3 D. This is completely new territory. ” Academic: “What? ” IBM Research Manager: “Every PC will be able to do 3 D. In IBM we do lots of graph drawing to model software. We think that 3 D graph drawing will become commonplace. ” Academic: “Really? ” IBM Research Manager: “There’s more space in 3 D, edge crossings can be avoided in 3 D, navigation in 3 D is natural”. Academic: “Really? ” IBM Research Manager: “If you do a 3 D graph drawing project, then IBM will fund it. ” Academic: “Let’s do it!” 50
1980 s 2 D Theorem: Every planar graph with maximum degree 4 admits a 2 D orthogonal drawing with no edge crossings and at most 4 bends per edge. . P Eades, C Stirk, S Whitesides, The techniques of Komolgorov and Bardzin for three dimensional orthogonal graph drawings Information Processing Letters, 1996 A Papakostas, I Tollis, Incremental orthogonal graph drawing in three dimensions - Graph Drawing, 1997 - Springer P Eades, A Symvonis, S Whitesides, Three-dimensional orthogonal graph drawing algorithms, Discrete Applied Mathematics, 2000 DR Wood, Optimal three-dimensional orthogonal graph drawing in the general position model, Theoretical Computer Science, 2003 1996 3 D Theorem: Every graph (even if it is nonplanar) with maximum degree 6 admits a 3 D orthogonal drawing with no edge crossings and a constant number of bends per edge. M Closson, S Gartshore, J Johansen, S Wismath, Fully dynamic 3 -dimensional orthogonal graph drawing, Graph Drawing, 1999 TC Biedl, Heuristics for 3 D-orthogonal graph drawings, Proc. 4 th Twente Workshop on Graphs and …, 1995 G Di Battista, M Patrignani, F Vargiu, A split&push approach to 3 D orthogonal drawing, Graph Drawing, 1998 D Wood, An algorithm for three-dimensional orthogonal graph drawing, Graph Drawing, 1998 M Patrignani, F Vargiu, 3 DCube: A tool for three dimensional graph drawing, Graph Drawing, 1997 51
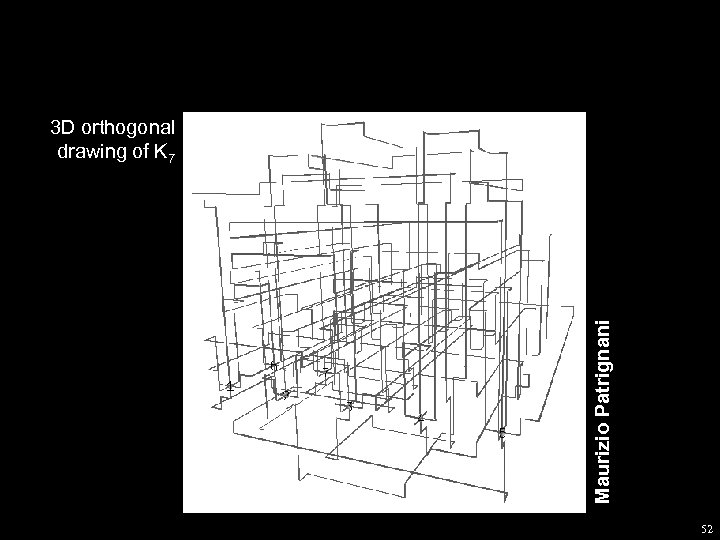Maurizio Patrignani 3 D orthogonal drawing of K 7 52
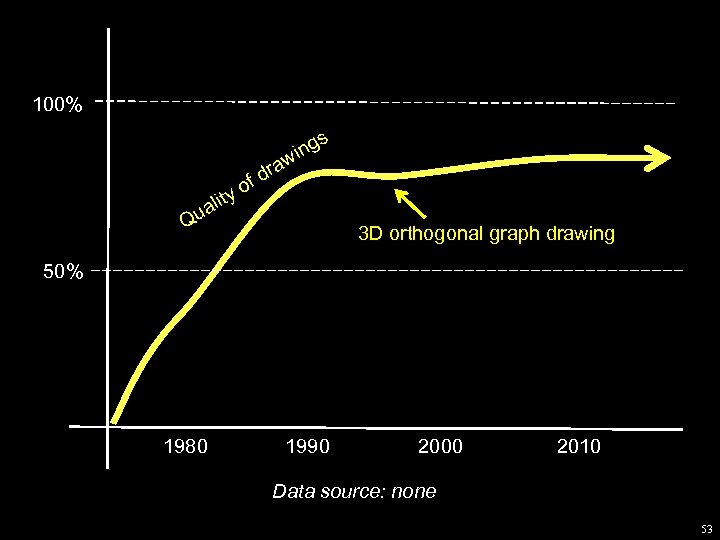100% s ty ali u d of ing w ra Q 3 D orthogonal graph drawing 50% 1980 1990 2000 2010 Data source: none 53
1990 – 2005: w Many theorems on 3 D w Many metaphors w Many research grants w Many experiments w A start-up company Mostly, 3 D failed. 54
2004+: success with 2. 5 D? Ø Colin Ware: “use 3 D with a 2 D attitude” Ø Tim Dwyer: “use third dimension for a single simple parameter (eg time)” Ø Seok. Hee Hong: “Multiplane method” 55
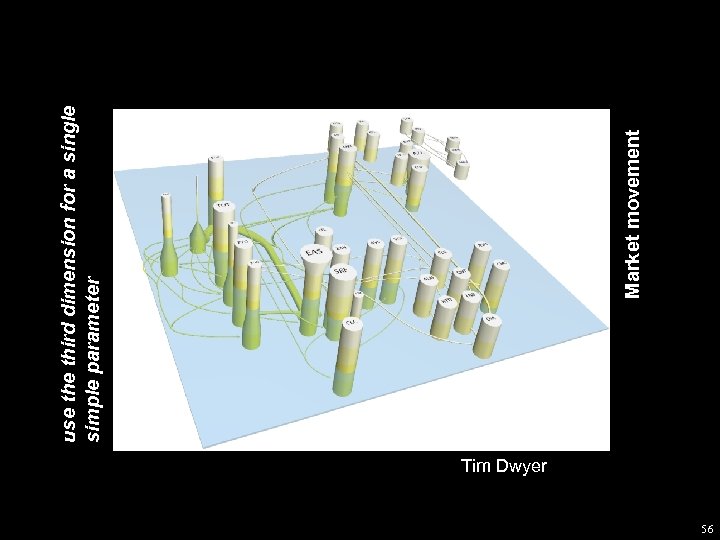Tim Dwyer 56 Market movement use third dimension for a single simple parameter
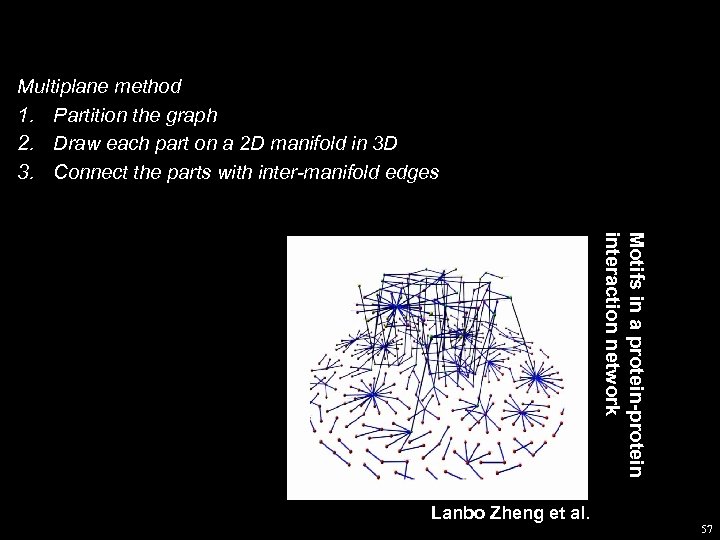Multiplane method 1. Partition the graph 2. Draw each part on a 2 D manifold in 3 D 3. Connect the parts with inter-manifold edges Motifs in a protein-protein interaction network Lanbo Zheng et al. 57
Joshua Ho 58
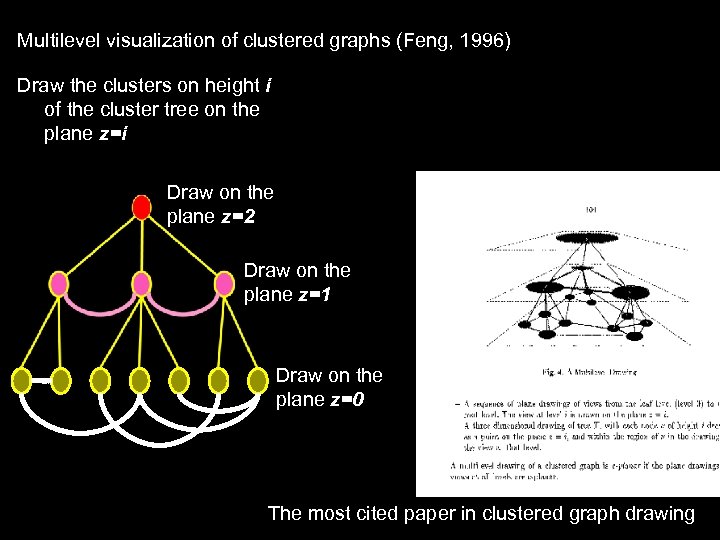Multilevel visualization of clustered graphs (Feng, 1996) Draw the clusters on height i of the cluster tree on the plane z=i Draw on the plane z=2 Draw on the plane z=1 Draw on the plane z=0 The most cited paper in clustered graph drawing 59
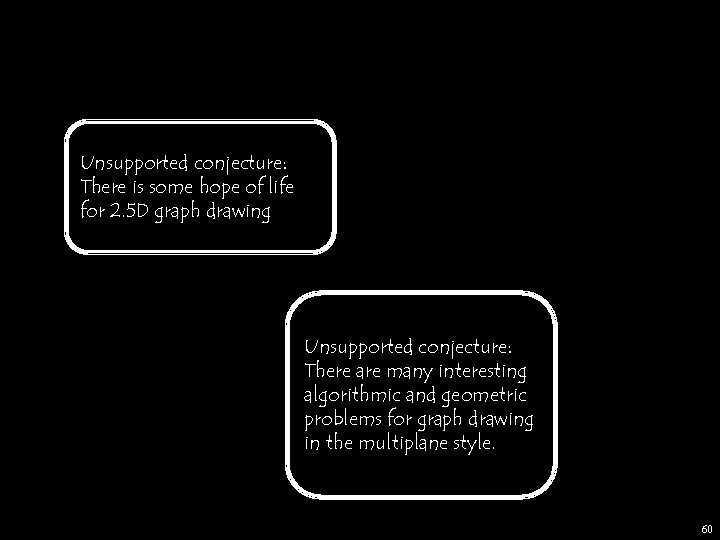Unsupported conjecture: There is some hope of life for 2. 5 D graph drawing Unsupported conjecture: There are many interesting algorithmic and geometric problems for graph drawing in the multiplane style. 60
Graph Drawing has proposed three approaches to the scale problem: 1. Use 3 D: spread the data over a third dimension 2. Use interaction: spread the data over time 3. Use clustering: view an abstraction of the data 61
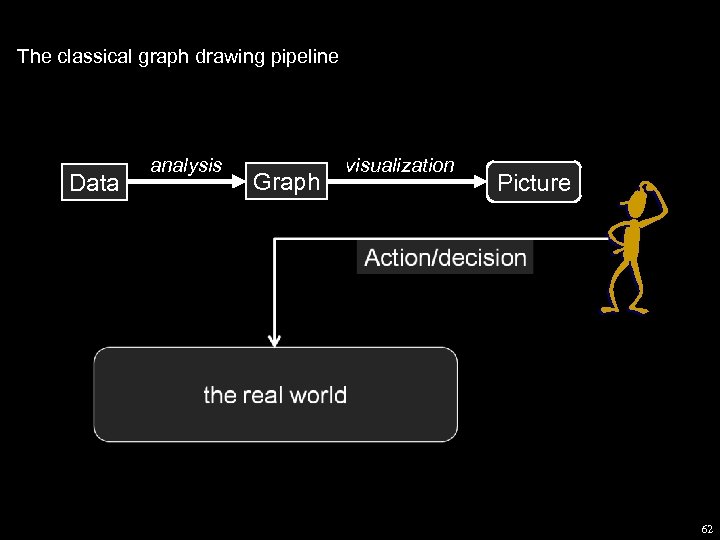The classical graph drawing pipeline Data analysis Graph visualization Picture 62
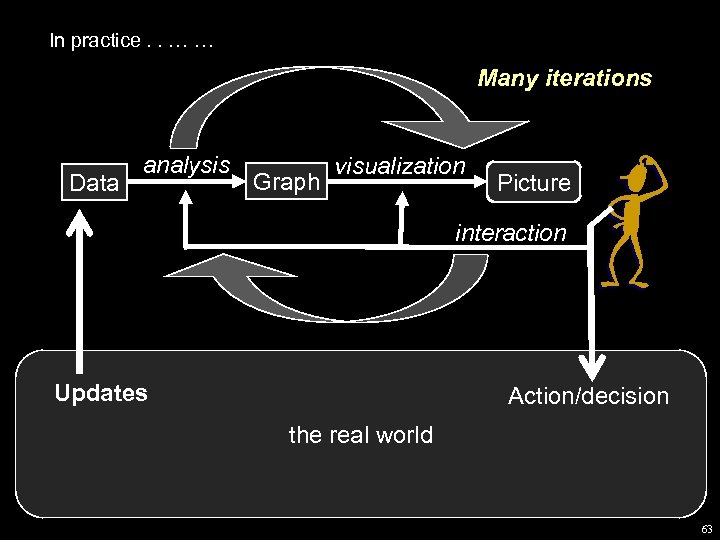In practice. . … … Many iterations Data analysis Graph visualization Picture interaction Updates Action/decision the real world. Action/decision 63
Interaction flow 1. 2. 3. 4. 5. The human looks at key frame Fi. The human thinks. The human clicks on something. System computes new key frame Fi+1. System computes in-betweening animation from key frame Fi to key frame Fi+1. 6. System displays animated transition from Fi to Fi+1. 7. i++ 8. Go to 1. Outrageous claim: all graph drawing algorithms need to be designed with interaction flow in mind 64
Interaction can solve both problems: Computational complexity: w The layout is only computed for the key frame (a relatively small graph) w The “user think time” can be used for computation Visual complexity: w At any one time, only a small graph is on the screen 65
Interaction also raises some problems: Cognitive complexity: w The user must remember stuff from one key frame to the next Ø “mental map” problem Unsupported conjecture: Interaction flow poses many interesting problems for graph drawing 66
Graph Drawing has proposed three approaches to the scale problem: 1. Use 3 D: spread the data over a third dimension 2. Use interaction: spread the data over time 3. Use clustering: view an abstraction of the data 67
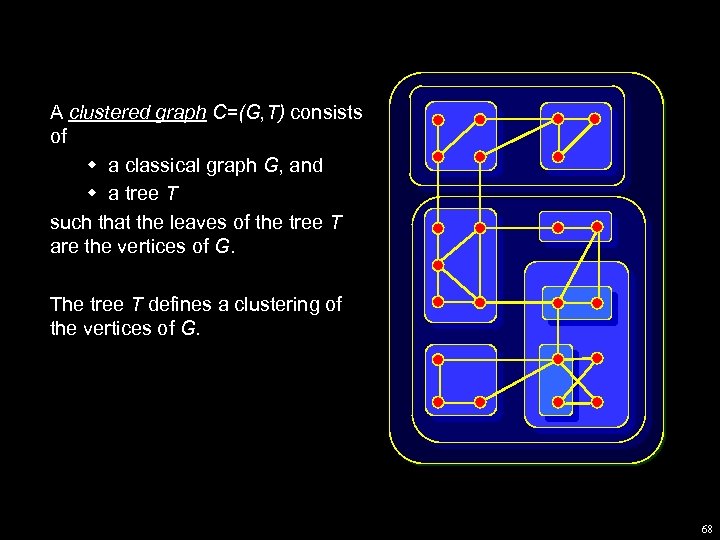A clustered graph C=(G, T) consists of w a classical graph G, and w a tree T such that the leaves of the tree T are the vertices of G. The tree T defines a clustering of the vertices of G. 68
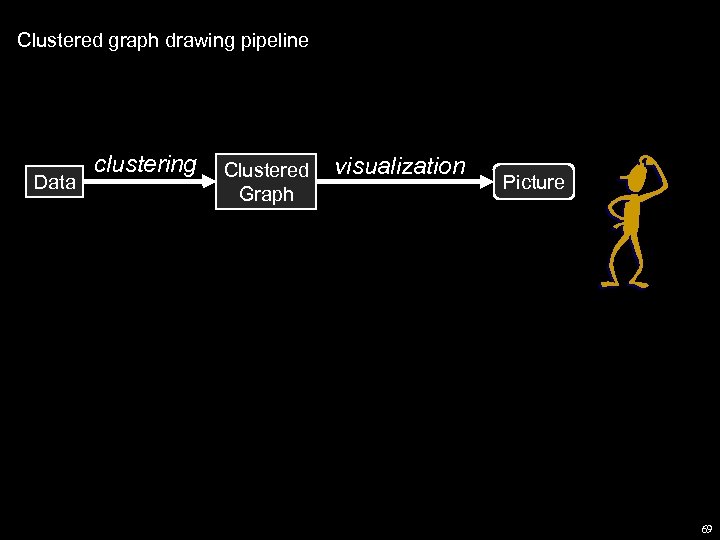Clustered graph drawing pipeline Data clustering Clustered Graph visualization Picture 69
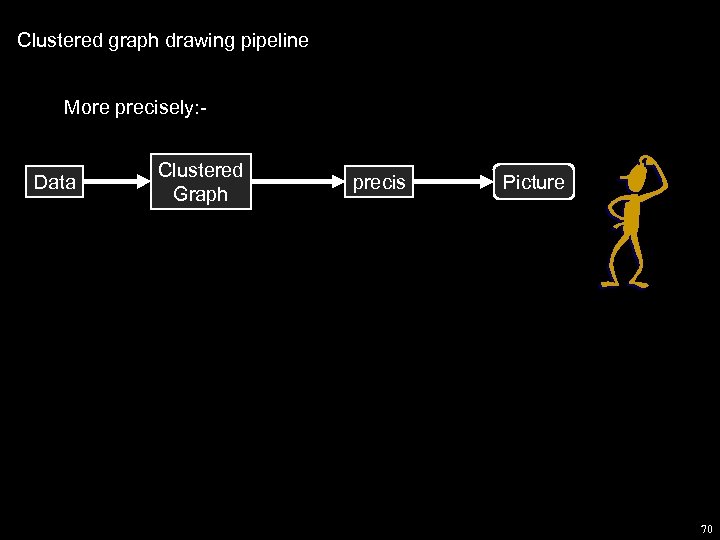Clustered graph drawing pipeline More precisely: - Data Clustered Graph precis Picture 70
We can only draw a part of a huge graph at a time. What part shall we draw? Ø A précis: a graph formed from an antichain in the cluster tree. A précis forms an abstraction of the data set. 71
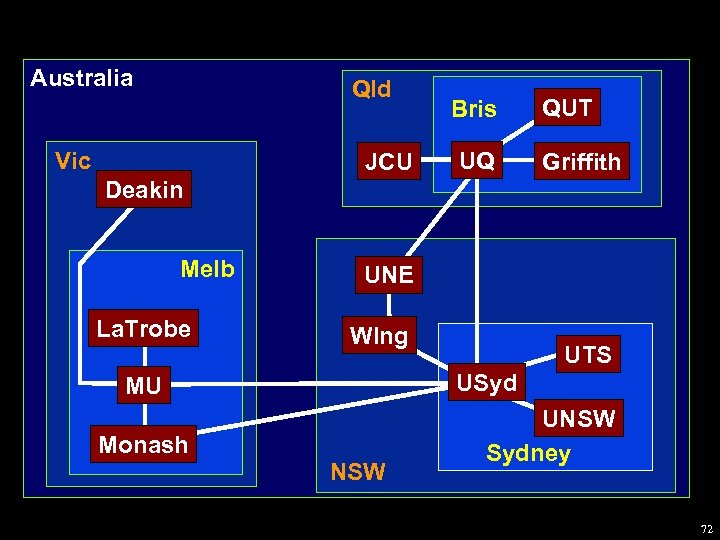Australia Qld Vic JCU Bris UQ QUT Griffith Deakin Melb La. Trobe UNE Wlng UTS USyd MU Monash NSW UNSW Sydney 72
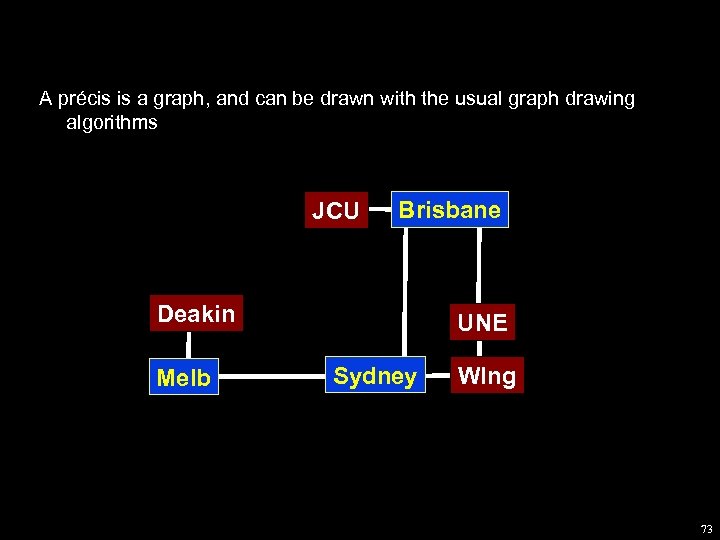A précis is a graph, and can be drawn with the usual graph drawing algorithms JCU Brisbane Deakin Melb UNE Sydney Wlng 73
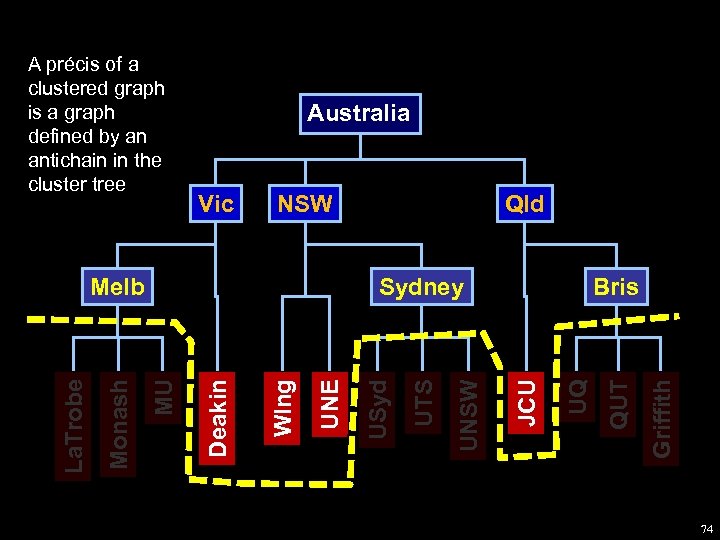Australia NSW UQ Bris JCU UNSW UTS USyd UNE Wlng Deakin Sydney MU Monash La. Trobe Melb Qld Griffith Vic QUT A précis of a clustered graph is a graph defined by an antichain in the cluster tree 74
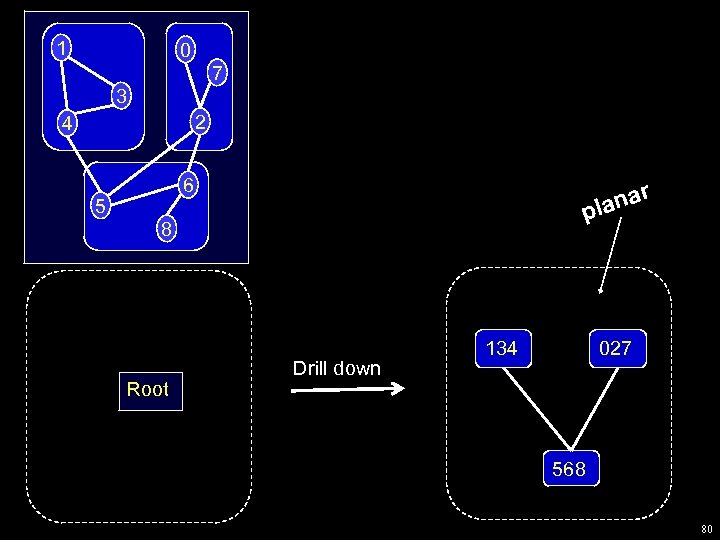
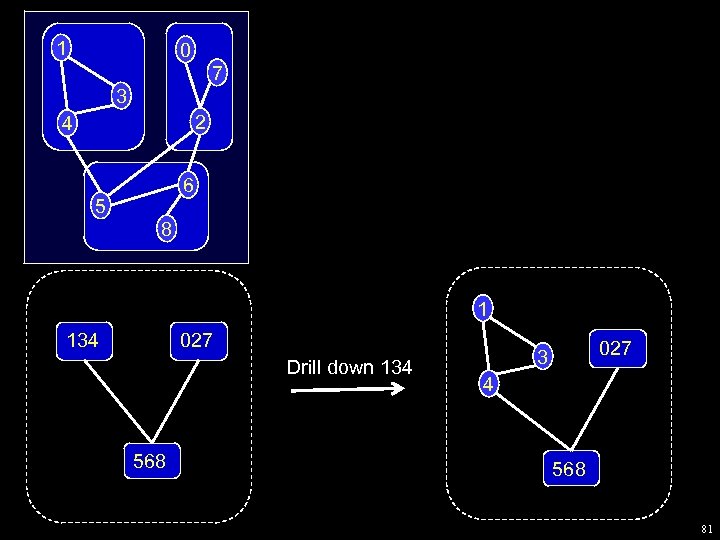
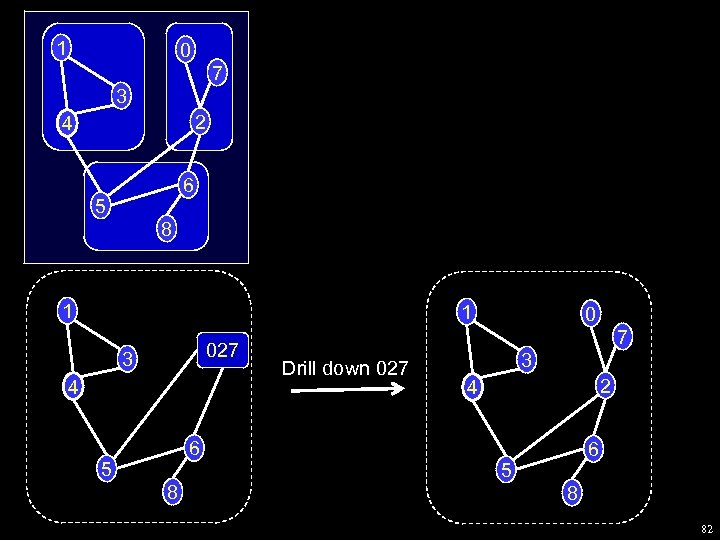
Drill down The basic human interaction with a clustered graph is drill down: w “Open” a node to see what it contains, that is, w i. e, replace a node in the antichain with it’s children. Also, we need drill-up: w “Close” a set of nodes to make the picture simpler w i. e, replace a set of siblings in the antichain with their parent Note: In practical systems w the human performs drill-down w the system performs drill-up 75
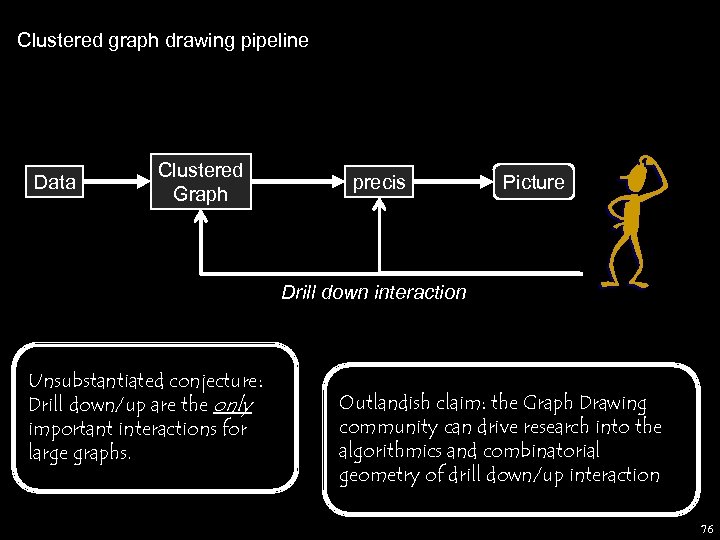Clustered graph drawing pipeline Data Clustered Graph precis Picture Drill down interaction Unsubstantiated conjecture: Drill down/up are the only important interactions for large graphs. Outlandish claim: the Graph Drawing community can drive research into the algorithmics and combinatorial geometry of drill down/up interaction 76
Michael Wybrow 77
For interaction: w “Drill down” on node X changes the size of X w “Drill up” should be performed by the system, not by the user w Nodes must move to accommodate change in size of node X w The new picture must be nice in the usual graph drawing sense w The mental map must be preserved: Ø Preserve orthogonal ordering Ø Preserve proximity Partially supported conjecture: Ø Preserve topology Graph drawing researchers can design algorithms to give good drill down/up interaction 78
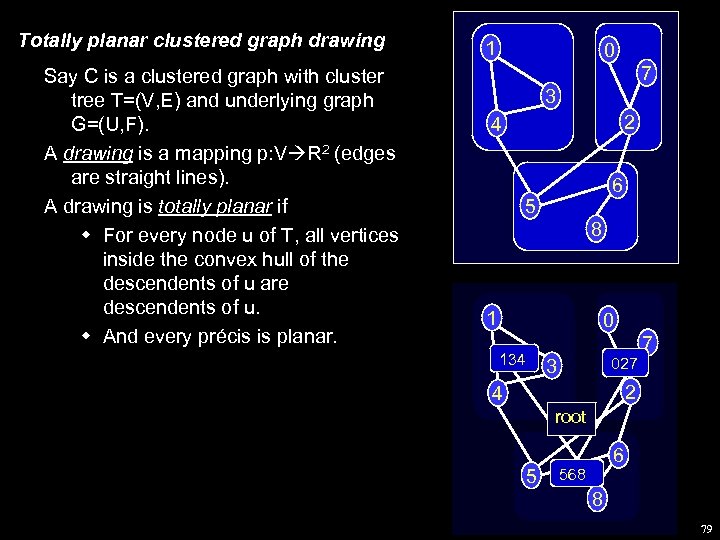Totally planar clustered graph drawing Say C is a clustered graph with cluster tree T=(V, E) and underlying graph G=(U, F). A drawing is a mapping p: V R 2 (edges are straight lines). A drawing is totally planar if w For every node u of T, all vertices inside the convex hull of the descendents of u are descendents of u. w And every précis is planar. 1 0 7 3 2 4 6 5 8 1 0 7 134 027 3 2 4 root 5 6 568 8 79
1 0 7 3 2 4 6 5 r lana p 8 Root Drill down 027 134 568 80
1 0 7 3 2 4 6 5 8 1 134 027 Drill down 134 568 027 3 4 568 81
1 0 7 3 2 4 6 5 8 1 1 027 3 4 6 5 8 0 7 Drill down 027 3 2 4 6 5 8 82
Open problem: Does every c-planar graph have a totally planar drawing? Equivalently: Almost equivalently: Open problem: Does every c-planar graph have straight-line multilevel drawing in which: Ø Every level is planar Ø The projection of a ith-level vertex onto level i-1 lies within the convex hull of its children 83
Unsubstantiated claim: The only chance for a solution to the scale problem for graph drawing lies in the algorithmics and geometry of interaction and clusters 84
Outrageous suggestion: Graph drawings are artworks 85
A personal timeline w Early 1980 s: I used intuition and introspection to evaluate graph drawings w Late 1980 s: I read Shneiderman’s book Ø Quality of an interface is a scientifically measurable function Ø Task time, error rate, etc w Now: I think graph drawings need to be beautiful as well as useful. w Katy Borner, 2009: "In order to change behaviour, data graphics have to touch people intellectually and emotionally. “ 86
Visual Connections Sydney June 2008 87
88
89
90
91
92
Outlandish claim: Graph drawings researchers have the skills needed to create graph drawing art 93
George Birkoff, 1933: w Beauty can be measured as a ratio M=O/C Ø O = “order” ~= Kolmogorov complexity Ø C = “complexity” ~= Shannon complexity Graph drawing problem as an optimization problem w A number of objective functions f: Drawings Real. Number w Given a graph G, find a drawing p(G) that optimizes f 94
Unsupported conjecture: Using Birkoff-style functions, graph drawing algorithms can produce art. 95
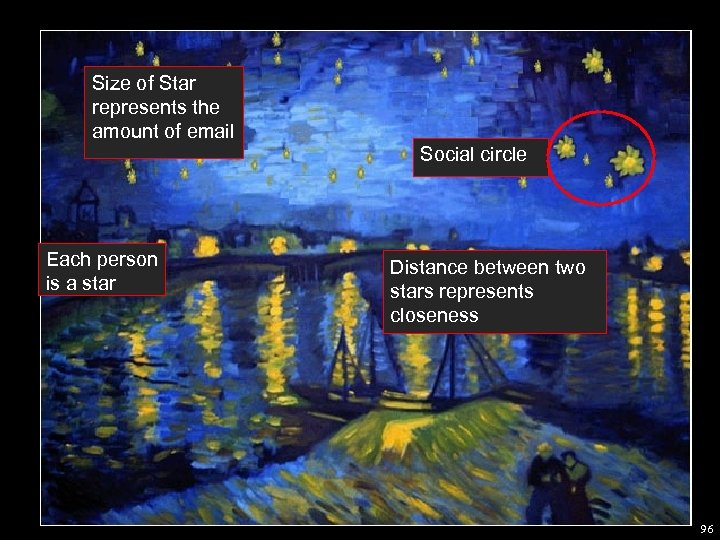Size of Star represents the amount of email Social circle Each person is a star Distance between two stars represents closeness 96
Currently: Graph drawing aims for Ø 100% information display, and Ø 0% art Outlandish suggestion: Graph drawing should have a range of methods, aiming for x% information display and (100 -x)% art, for all 0 <= x <= 100 97
Open problem: Use integer linear programming to produce valuable graph drawing art. + 10 $ 98
Open problem: Why do force directed methods work? 99
Force directed methods w There have been many experiments w A few more theorems would be good One theorem has been proved: If a graph has the right automorphisms, then there is a local minimum of a spring drawing that is symmetric. Some theory exists w Combinatorial rigidity theory w Theory of multidimensional scaling But there are many questions that I don’t know the answer Warning : this is i ntrospec t ive resea rch! 100
Open problem: How many local minima are there? Open problem: How close are Euclidean distances to the graph theoretic distances? Open problem: What is the time complexity of a spring algorithm? Open problem: Do force directed methods give bounded crossings most of the time? 101
This is the end of the rhapsody of unsupported conjectures, subjective observations, outlandish claims, a few plain lies, and open problems 102
Back to the main question: w What is the future of Graph Drawing? w Where does the road lead? 103
Where does the road lead? 104
105
106
107
ter Pe 108
Question: What is the future of Graph Drawing? . . . Sorry, I’ve run out of time. 109
Question: What is the future of Graph Drawing? Answer: it’s up to you. 110
Many thanks 111