634fb4bda7fcebcb97baba70aacccbc8.ppt
- Количество слайдов: 21

The Fable of Eric

Eric was born in Alaska in 1970 s. He lived happily in a beautiful Victorian house facing the sea…

Thirty years later, global warming made the coastline erode. Eric’s childhood house was about to collapse.

To save millions of Eric’s houses, government demanded the electricity come from renewable energy by 2025. 25% of • Billions of dollars in stimulus plan (www. usnews. com) • 31 states: Renewable Energy Portfolio Standards (RPS) • NYISO: 30% by 2013 Eric wanted to be part of the solution to save his Victorian house.

He hired a few people to set up a wind farm and put together some solar panels.

He sells the electricity to an ISO and finds out he can barely make a living: • Price and wind generation negatively correlated: • • The wind tends to blow the strongest at night when the price is the lowest, sometimes even negative. Penalty fee/ imbalance cost • • • Bidding: Advanced contracting Forecast error 30%~50% Entering into a long-term contract

• • Someone advises him to buy a big battery: • Store when price is low/ or there is excess • Sell when the price is high. The catch is that battery is expensive. • 1 MW Na. S costs $1 M? Is it worth it? Can I get my investment back? • When? How?

Intermittent Resources with Storage in a Deregulated Electricity Market Yangfang Zhou, Stephen Smith, Alan Scheller-Wolf, Nicola Secomandi

Contents 9 Literature Review Who we are and what we do OM perspective Our model High level model, Sequence of events, Research questions Results: optimal policy, value of the storage Compare (preliminary) Future work

Literature Review 10 Electricity Generation and Storage Joint optimization of wind-hydro plant Gonzalez et al. 2008 (1 generator &1 storage, SP, no analytical result) Economic Dispatch of Intermittent Resources Xie et al. 2008 (Do not consider storage. ) Electricity storage evaluation Walawalkar & et al. 2008 (data: arbitrage in different markets) … many others Inventory Theory and Commodity Storage Trace back 50 years Secomandi 2009 : Commodity trading Optimal inventory policy for batteries coupled with intermittent generators in an electricity market & value of storage is still open.

Operations Management 11 What does operations Management do? Create and use operations research techniques Optimize business operations : inventory Dynamic programming Linear/Integer programming Stochastic programming Constraint programming …. . . store, how When to order, how much to store much to order Electricity is a special type of perishable inventory Bridge OM & electricity
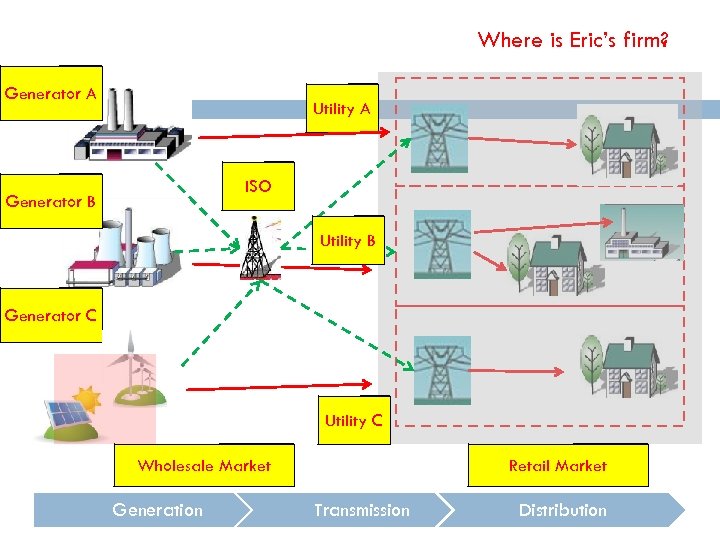
Where is Eric’s firm? Generator A Utility A ISO Generator B Utility B Generator C Utility C Wholesale Market Generation Retail Market Transmission Distribution
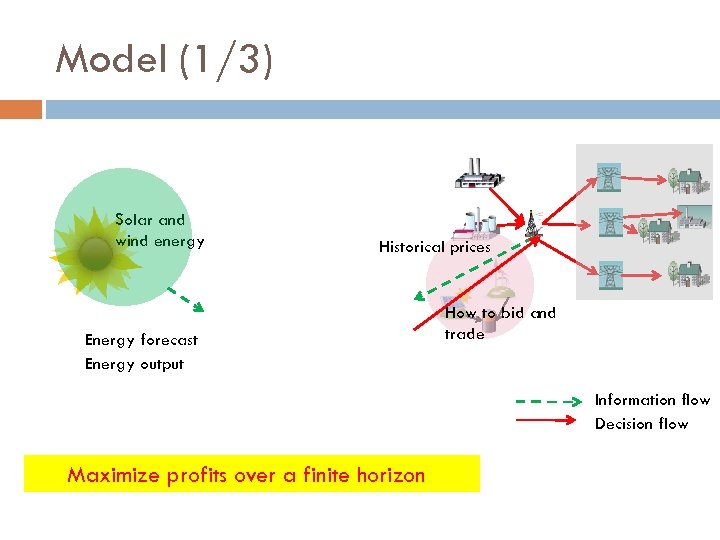
Model (1/3) Solar and wind energy Historical prices Energy forecast Energy output How to bid and trade Information flow Decision flow Maximize profits over a finite horizon
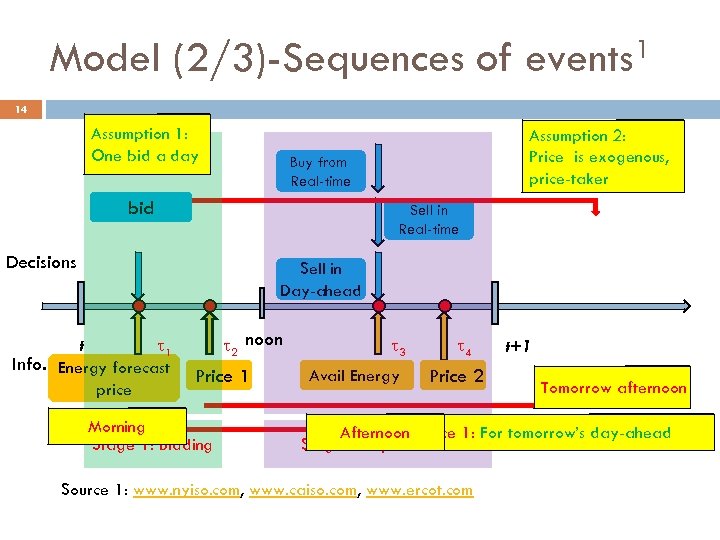
Model (2/3)-Sequences of events 1 14 Assumption 1: One bid a day Assumption 2: Price is exogenous, price-taker Buy from Real-time bid Sell in Real-time Decisions Sell in Day-ahead t 1 Info. Energy forecast price 2 noon Price 1 Morning Stage 1: Bidding 3 Avail Energy 4 Price 2 t+1 Tomorrow afternoon Afternoon Price 1: For tomorrow’s day-ahead Stage 2: Operational Source 1: www. nyiso. com, www. caiso. com, www. ercot. com
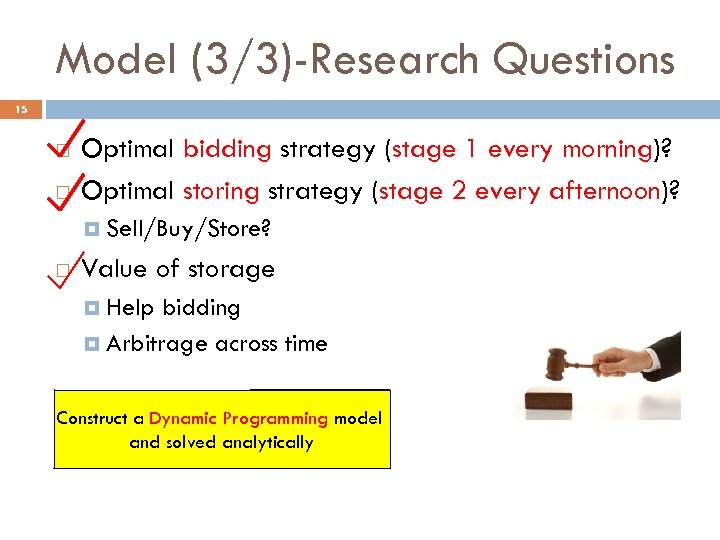
Model (3/3)-Research Questions 15 Optimal bidding strategy (stage 1 every morning)? Optimal storing strategy (stage 2 every afternoon)? Sell/Buy/Store? Value of storage Help bidding Arbitrage across time Construct a Dynamic Programming model and solved analytically
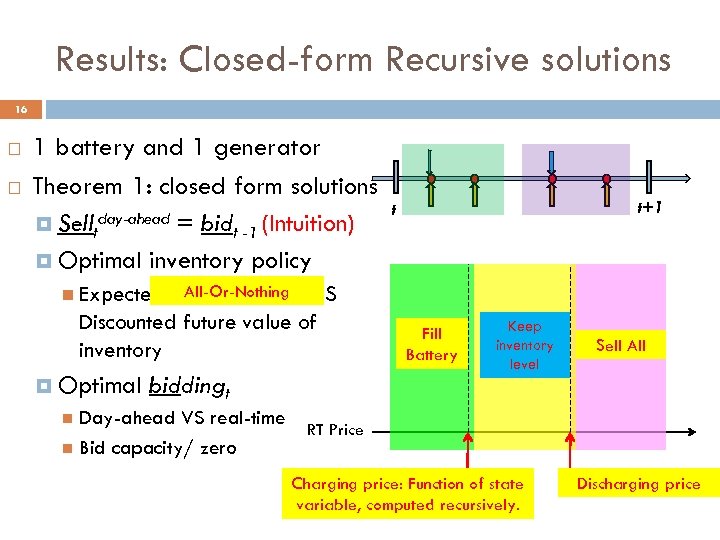
Results: Closed-form Recursive solutions 16 1 battery and 1 generator Theorem 1: closed form solutions Selltday-ahead = bidt -1 (Intuition) Optimal inventory policy All-Or-Nothing real-time price VS Discounted future value of inventory t+1 t Expected Optimal biddingt Day-ahead VS real-time Bid capacity/ zero Fill Battery Keep inventory level Sell All RT Price Charging price: Function of state variable, computed recursively. Discharging price
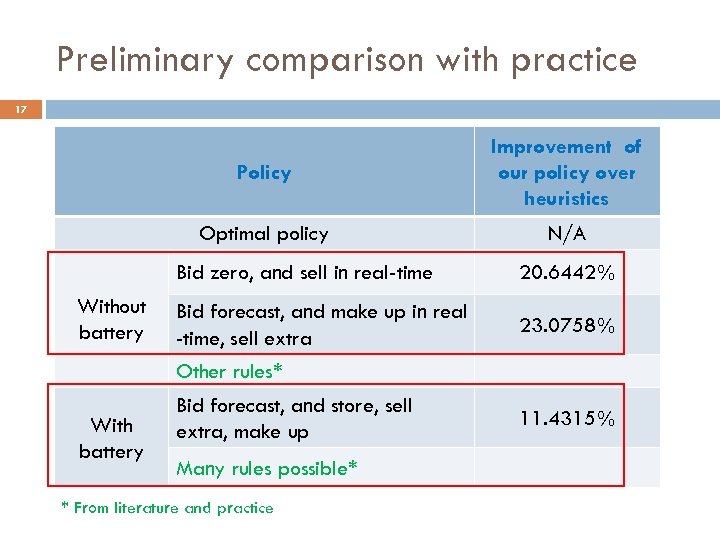
Preliminary comparison with practice 17 Policy Improvement of our policy over heuristics Optimal policy N/A Bid zero, and sell in real-time Without battery 20. 6442% Bid forecast, and make up in real -time, sell extra 23. 0758% Other rules* With battery Bid forecast, and store, sell extra, make up Many rules possible* * From literature and practice 11. 4315%

Future work 18 Calibrate price models with more data Use financial models Waiting for more data from CME… Benchmark literature and practice Value of storage How good is our policy over heuristics and practice? R. O. I. Storage value to balance network For the whole grid, how much battery is needed for security and economic concerns

19 Thank you. Questions?

Appendix 20
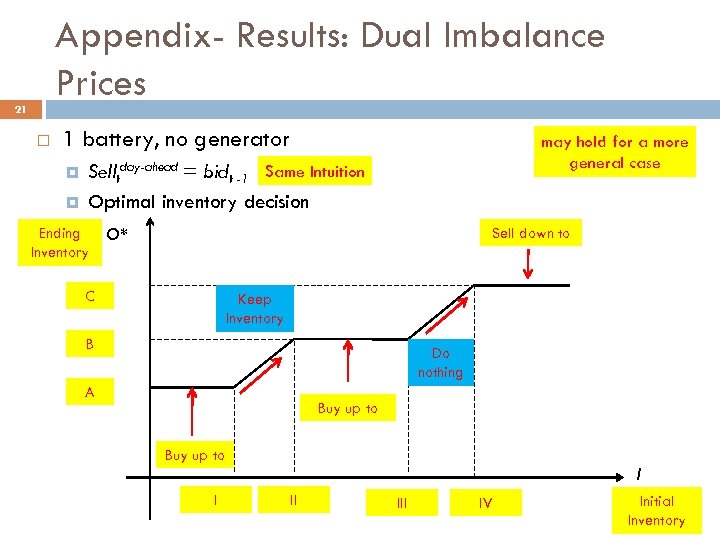
Appendix- Results: Dual Imbalance Prices 21 1 battery, no generator may hold for a more general case Selltday-ahead = bidt -1 Same Intuition Optimal inventory decision Ending Inventory O* Sell down to C Keep Inventory B Do nothing A Buy up to I I II IV Initial Inventory
634fb4bda7fcebcb97baba70aacccbc8.ppt