b25745c347458f0f36d4bd6d79f1ca39.ppt
- Количество слайдов: 16

The Duality between Planar Kinematics and Statics Dr. Shai, Tel-Aviv, Israel Prof. Pennock, Purdue University


The Outline for the tutorial: A Study of the Duality between Kinematics and Statics • Two new concepts for statics that are derived from kinematics: Equimomental line and face force. • Transforming theorems and rules between kinematics and statics. • Characterizing and finding dead center positions of mechanisms and the stability of determinate trusses. • Correlation between Instant Centers and Equimomental Lines. • Graph theory duality principal and the dual of linkages – trusses. • Detailed example of the face force and the procedure for deriving the face force. • Transforming Stewart platforms into serial robots and vice versa. • Checking singularity through the duality transformation. • Applying the duality transformation for systematic conceptual design. • Discussion and suggestion for future research in this area
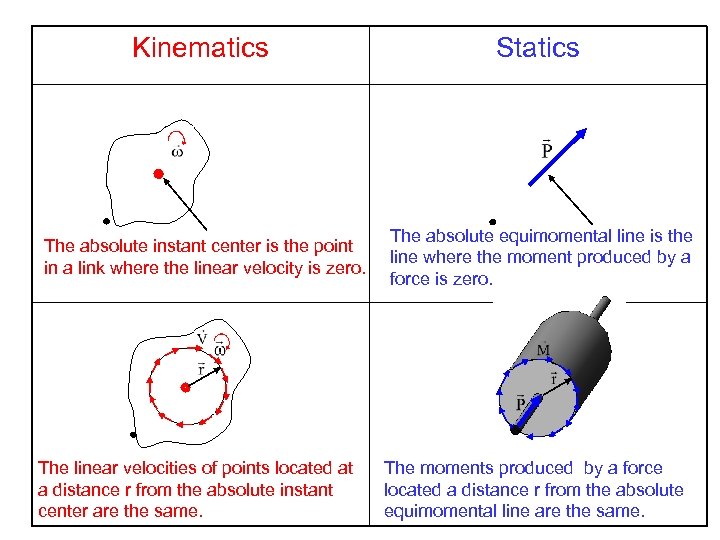
Kinematics Statics The absolute instant center is the point in a link where the linear velocity is zero. The absolute equimomental line is the line where the moment produced by a force is zero. The linear velocities of points located at a distance r from the absolute instant center are the same. The moments produced by a force located a distance r from the absolute equimomental line are the same.
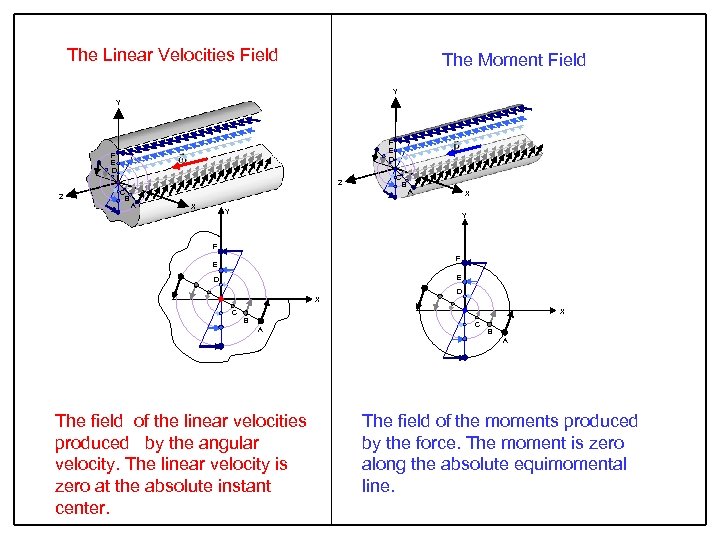
The Linear Velocities Field The Moment Field Y Y F E D Z Z C B A X Y Y F F E E D X C B A The field of the linear velocities produced by the angular velocity. The linear velocity is zero at the absolute instant center. The field of the moments produced by the force. The moment is zero along the absolute equimomental line.
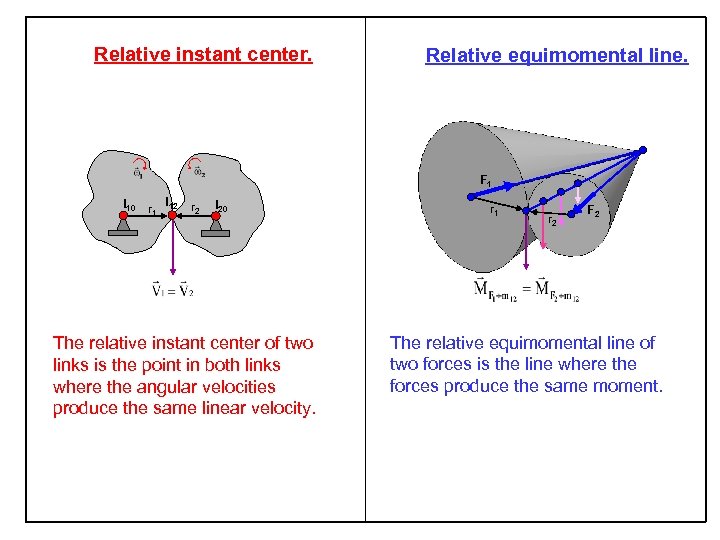
Relative instant center. Relative equimomental line. F 1 I 10 r 1 I 12 r 2 I 20 The relative instant center of two links is the point in both links where the angular velocities produce the same linear velocity. r 1 r 2 F 2 The relative equimomental line of two forces is the line where the forces produce the same moment.
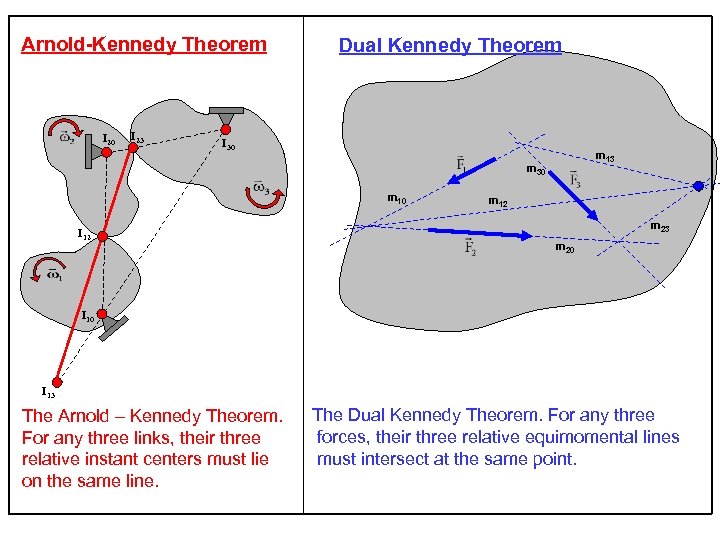
Arnold-Kennedy Theorem I 20 I 23 Dual Kennedy Theorem I 30 m 13 m 30 m 10 I 12 m 23 m 20 I 13 The Arnold – Kennedy Theorem. For any three links, their three relative instant centers must lie on the same line. The Dual Kennedy Theorem. For any three forces, their three relative equimomental lines must intersect at the same point.
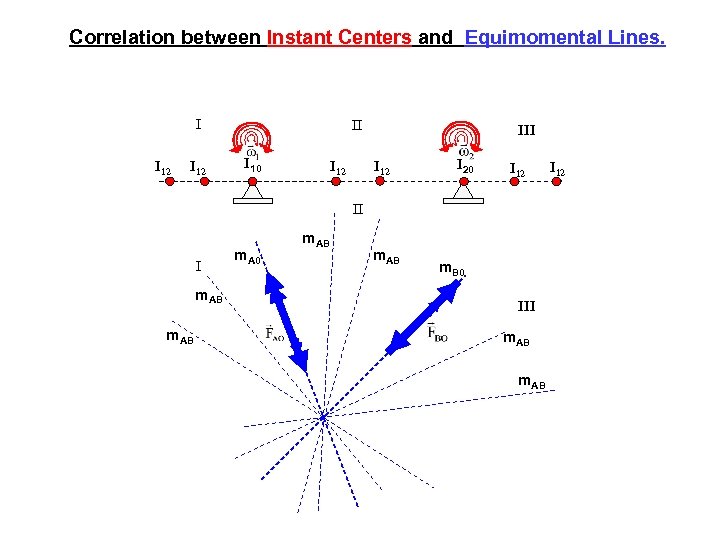
Correlation between Instant Centers and Equimomental Lines. I I 12 II I 10 I 12 III I 12 I 20 I 12 II I m. AB m. A 0 m. AB m. B 0 III m. AB I 12

The idea behind the transformation of Kinematic systems (Linkages) into Static systems (determinate trusses) • Each engineering system can be represented into mathematical model based on graph theory. • There are mathematical relations between the graph representations such as the graph theory duality. • For example, the representations of linkages and trusses were found to be dual. Thus, linkages and determinate trusses are dual systems. The following slides will show the process of constructing dual engineering systems on the basis of the graph theory duality principle.
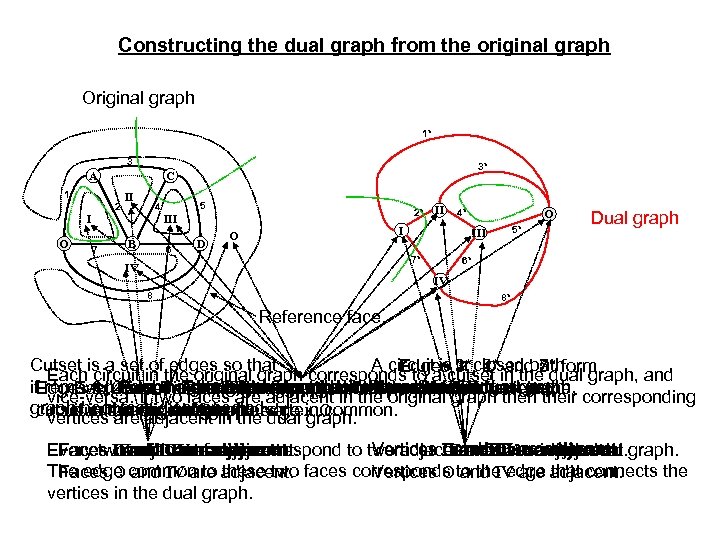
Constructing the dual graph from the original graph Original graph 1* 3 A 1 2 II 5 4 I O 3* C 2* III 7 B 6 D II 4* I O 5* III 7* IV O Dual graph 6* IV 8 8* Reference face. Cutset is a set of edges so that A circuit is 3*, 4* and 5* form a closed path. Edges 1*, 2* 7* Each circuit in the original graph corresponds to a cutset in the dual graph, and if. Edges 3, 4 from the. Two faces area circuittocorrespondsindual graph. removed 2 cutsetface in originalis adjacent thevertextothecircuit graph. III II I thevertex IV. cutset circle the IVcorresponds Each A face in. Face the correspondstowithout innerintodual in the 1, Each 5 constitute original. O correspondshave edges. and 7 ingraph, corresponds in they I. III. a vertex the graph to the avertex. II. vice-versa. If two Referenceadjacent correspondsto graph then their corresponding faces area face graph if original aat graphdualthe original graph. edge in. O. in adjacent in versa. reference cutsetbecomes disconnected. dual graph. circuit in graph, and vice the vertex common. least one vertices arethe dual graph. II and. IV are adjacent. Every twoand IVare faces correspond to two adjacentand. Oare adjacent. graph. Faces I and. IIIVareadjacent. III O and. O are adjacent. III are adjacent. I Vertices Oand IIIVareinadjacent. III vertices adjacent. I III are the dual I The edge common to adjacent. faces corresponds to the edge adjacent. Faces O and IV are these two Vertices O and IV are that connects the vertices in the dual graph.

Augmenting the geometry Constructing the dual graph. to The meaning of a directed edge in the dual Constructinggraph. the its topology. graph: O Kinematic system. Constructing the B corresponding graph 3 e=<t, h> is the flow 3(force) acting upon the (CCW) B 2* 4* A A head vertextopology arrow and (rod). (CCW) The (joint) by the edge the force arrow are in (CW) 3* the same direction -> compression. 2 4 The force in rod 4** acts upon the ground 2 4 Inverse directions - tension 4 I Two choices? externalacts in rod upon in this orientation. The direction of the forceupon the ground force in rod 3** force acts 4**. The (CW) 2 (CW) in this Vertex I corresponds to joint I. 3**. orientation. joint The direction of the. Iforce in rod (CW) O O O Thecompression. type is tension. The type is O O 2 O 1 1 Adding 1 geometry. the 4 2 4 3 Edge. Link 2 is. Vertex velocity. Thevelocity Faces the to. Othe 2, is between the two 2 The relative velocities link 2 corresponds edgerespectively. 2. is the potential 3 correspond Edgesource, directionadjacent. therelativecorresponds tojoints 4 I. and O, are to the edge Edge contract the toand O correspond thethe driving linear potentiallink with Vertex 2 corresponds 3 corresponds 4 Theand OO corresponds tothe drivingtwo of links joint 3. 3 to of link Vertices B yields Asourceofthat toto joint is 2 commonfixed link 1, adjacent faces O 4 can link. consistency, A. The kinematic analysis Weand 1 correspondedges B and the For Edges 4 potentialof edge 2. and O 4. and in 4 dualoriginal graph. toand O the edge 4* is between the link thus the 4 3** potential difference faces Ito is O face Oby dual edge 3* is to the differences difference. Reference thus the rotating difference adjacent. Ifaces Iand defined corresponds to of edges 3 4** magnitudes and directions oforiginalin 4 dual graphzero. the and the Potential differences respectively. graph two adjacent vertices I and O. in edges 23 angular equal of the edge Therefore, in the dualvertex O. corresponds I and O. between the two adjacent vertices to the reference graph it and relative linear velocities. 3*graph. edge in the original graph in CCW I. edges corresponds Ito the in the edge and 4*. correspond to flowsflow in dual 2*. the source. Face it is between the two adjacent I corresponds to vertex flow Building the direction. and 4** vertices I truss. correspondingand O. 4 3** O 3 (tension) (compression) Constr The angular velocity in e angular to com is Thrrespondsvelocitypre co corresponds to a tensi The corresponding truss O 4 The dual graph.

Since linear developed a new variable in We have systematicallyvelocity is associated with a statics: We obtain the dual systems. dual joint in the linkage, its dual variable is B this What Joint first, whatto the face in thevelocity? of the joint is a At counterpart is absolute linear. Face velocity associated with dual absolute truss O 3 The relative 1. The absoluteof the input linkhas a property of potential. rod 3**. linear velocity linearlink 3 corresponds to the external force. 4 4**. velocity corresponds to force in the Velocity Force A + + 3 On the other hand. Why? that velocity we 4 dual know Absolute linear velocity corresponds to. Force 3** Velocity of a joint to force. Face force. corresponds Because, We can give any absolute velocities to the links, and 4** they will satisfy the rule of velocities (vectors KVL). 2 O 4 1 1 I O 4
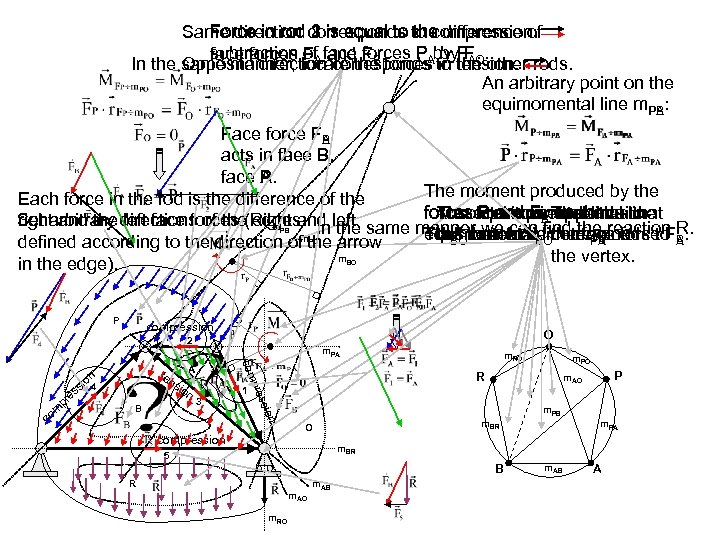
1 Same direction corresponds to compression. Force in rod 2 is equal to the difference of 3 subtraction FA face FB. F by F. face forces of and forces PAby FAO. In the same manner, locate the forces to tension. rods. Opposite direction corresponds in the other An arbitrary point on the equimomental line m. PA: PB Face force FP B A acts in the B. face P. A. The moment produced by the Each force in the rod is the difference of the forcescircuit corresponds line upon the Absolute equimomental to The P and FB Thethe A on lines Set arbitrary directions of the(Right and left same mannerequimomental circuitthat R. right and the left face forces edges. In the m we can determined. Thus locate m line m. PB. reaction B equimomental. BOcorresponds to A. m. BOvertex. befind the force F the has to will we obtain the face. m PA defined according to the direction of the arrow the vertex. m in the edge). PB PO BO P compression O 2 1 n ssio B 3 m. RO m. PO R pre m co com sio n e pr A ten n io ss 4 m. PA P m. AO m. PB m. BR O compression m. PA m. BR 5 B R m. AO m. RO m. AB A
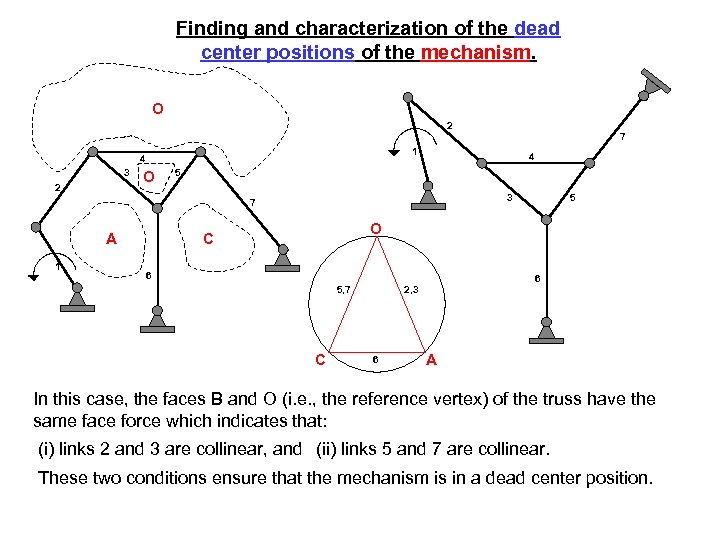
Finding and characterization of the dead center positions of the mechanism. O 2 7 1 4 3 2 O 4 5 A 1 5 3 7 O C 6 2, 3 5, 7 6 A In this case, the faces B and O (i. e. , the reference vertex) of the truss have the same face force which indicates that: (i) links 2 and 3 are collinear, and (ii) links 5 and 7 are collinear. These two conditions ensure that the mechanism is in a dead center position.
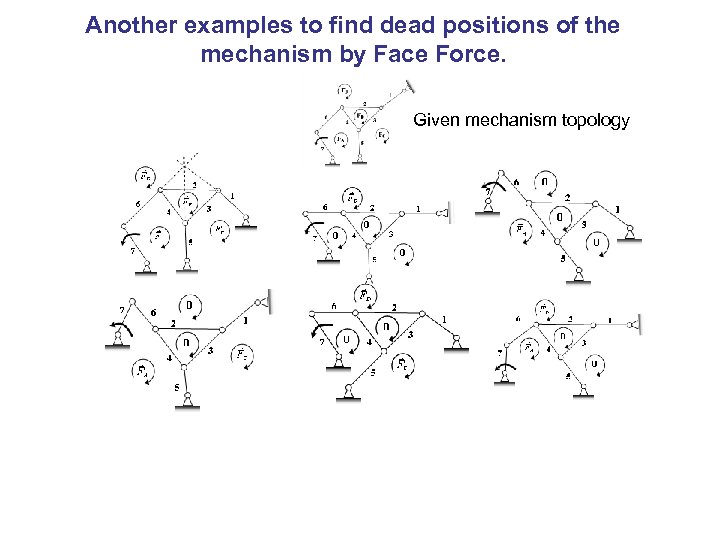
Another examples to find dead positions of the mechanism by Face Force. Given mechanism topology
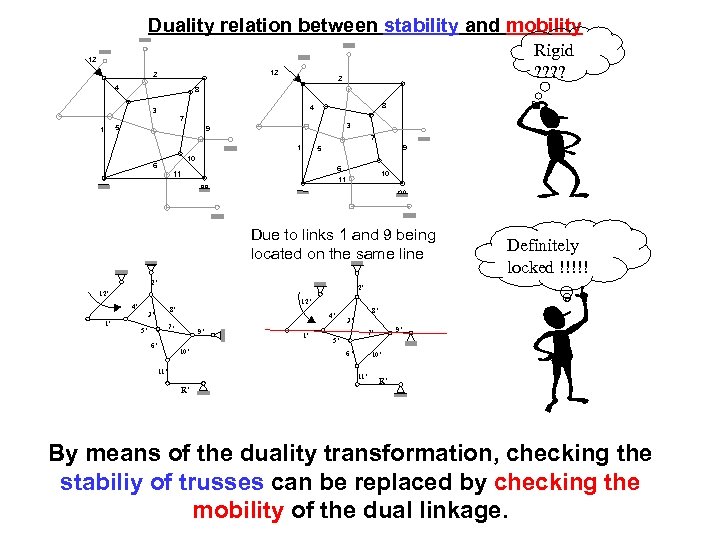
Duality relation between stability and mobility Rigid ? ? 12 12 2 4 8 4 3 7 5 1 2 8 3 9 7 1 9 5 10 6 6 11 10 11 Due to links 1 and 9 being located on the same line 2’ 2’ 12’ 4’ 12’ 8’ 3’ 1’ Definitely locked !!!!! 4’ 7’ 5’ 6’ 9’ 10’ 11’ 1’ 8’ 3’ 6’ 10’ 11’ R’ 9’ 7’ 5’ R’ By means of the duality transformation, checking the stabiliy of trusses can be replaced by checking the mobility of the dual linkage.
b25745c347458f0f36d4bd6d79f1ca39.ppt