The diffuse dynamics of choice MURI Center for

The diffuse dynamics of choice MURI Center for Human and Robot Decision Dynamics, Sept 13, 2007. Phil Holmes, Jonathan Cohen + many collaborators. From T. Mc. Millen & P. Holmes, J. Math. Psych. 50: 30 -57, 2006.

A really simple decision task: “On each trial you will be shown one of two stimuli, drawn at random. You must identify the direction (L or R) in which the majority of dots are moving. ” The experimenter can vary the coherence of movement (% moving L or R) and the delay between response and next stimulus. Correct decisions are rewarded. “Your goal is to maximize rewards over many trials in a fixed period. ” A speed-accuracy tradeoff. . 30% coherence 5% coherence Courtesy: W. Newsome Behavioral measures: reaction time distributions, error rates. More complex decisions: buy or sell? Neural economics.

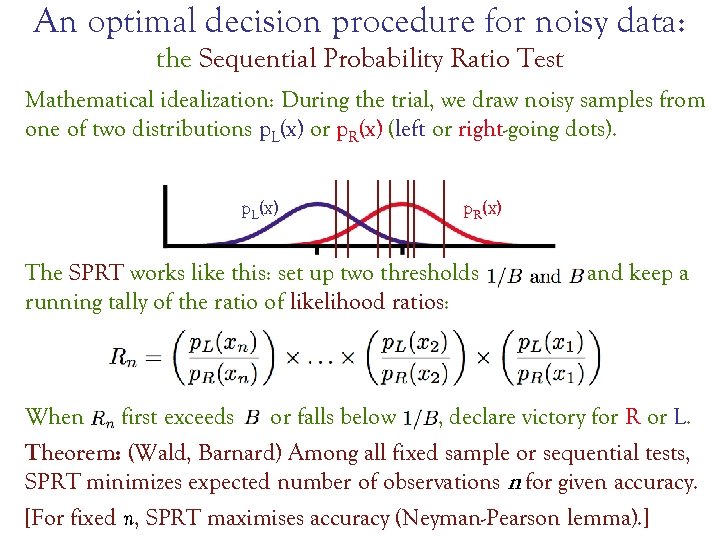An optimal decision procedure for noisy data: the Sequential Probability Ratio Test Mathematical idealization: During the trial, we draw noisy samples from one of two distributions p. L(x) or p. R(x) (left or right-going dots). p. L(x) p. R(x) The SPRT works like this: set up two thresholds running tally of the ratio of likelihood ratios: and keep a When first exceeds or falls below , declare victory for R or L. Theorem: (Wald, Barnard) Among all fixed sample or sequential tests, SPRT minimizes expected number of observations n for given accuracy. [For fixed n, SPRT maximises accuracy (Neyman-Pearson lemma). ]

The continuum limit is a DD process Take logarithms: multiplication in becomes addition. Take a continuum limit: addition becomes integration. The SPRT becomes a drift-diffusion (DD) process (a cornerstone of 20 th century physics): drift rate noise strength Here is the accumulated evidence (the log likelihood ratio). When reaches either threshold , declare R or L the winner. But do humans (or monkeys, or rats) drift and diffuse? Evidence comes from three sources: behavior, direct neural recordings, and mathematical models.

Behavioral evidence: RT distributions Human reaction time data in free response mode can be fitted to the first passage threshold crossing times of a DD process. thresh. +Z drift A thresh. -Z Prior or bias toward one alternative can be implemented by starting point . (Ratcliff et al. , Psych Rev. 1978, 1999, 2004, … )

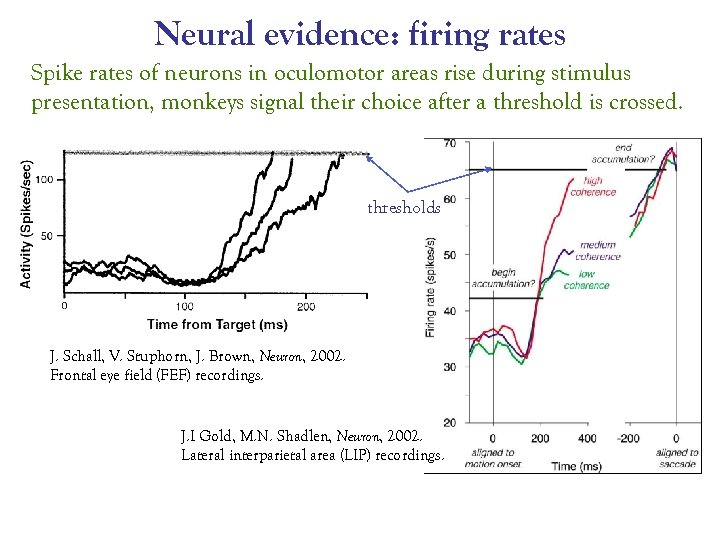Neural evidence: firing rates Spike rates of neurons in oculomotor areas rise during stimulus presentation, monkeys signal their choice after a threshold is crossed. thresholds J. Schall, V. Stuphorn, J. Brown, Neuron, 2002. Frontal eye field (FEF) recordings. J. I Gold, M. N. Shadlen, Neuron, 2002. Lateral interparietal area (LIP) recordings.

An optimal speed-accuracy tradeoff 1 The task: maximize rewards for a succession of free response trials in a fixed period. RT D Reward Rate: (% correct/average time between resps. ) response-to-stimulus interval • Threshold too low X $ D RT RT D $ X RT D RT $ • Too high RT RT D $ D D D $ $ • Optimal X RT RT $ X D RT

An optimal speed-accuracy tradeoff 2 How fast to be? How careful? The DDM delivers an explicit solution to the speed-accuracy tradeoff in terms of just 3 parameters: normalized threshold and signal-to-noise ratio and D. So, setting the threshold we can express RT in terms of ER and calculate a unique, parameter-free Optimal Performance Curve: RT/D = F(ER)

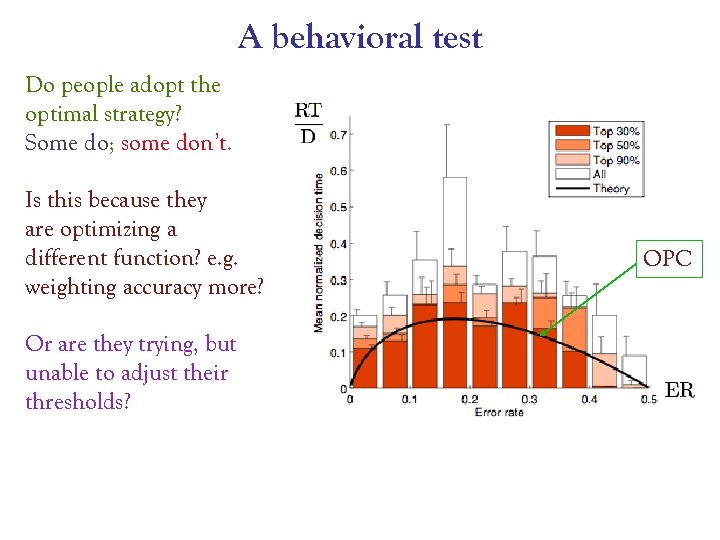A behavioral test Do people adopt the optimal strategy? Some do; some don’t. Is this because they are optimizing a different function? e. g. weighting accuracy more? Or are they trying, but unable to adjust their thresholds? OPC

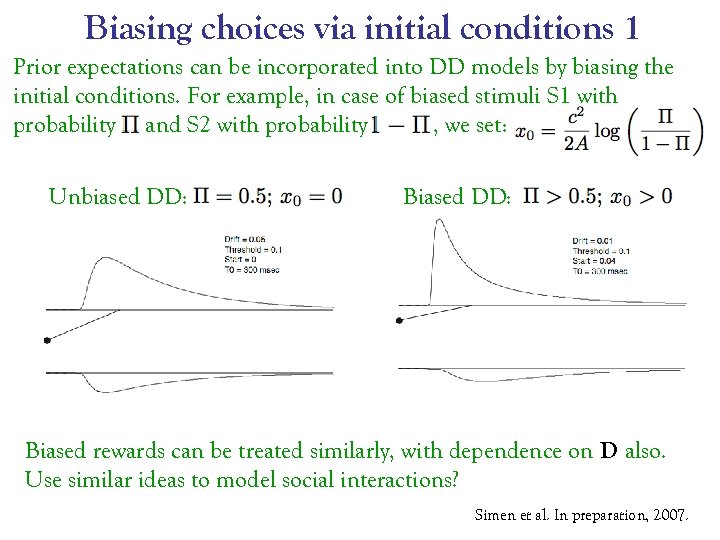Biasing choices via initial conditions 1 Prior expectations can be incorporated into DD models by biasing the initial conditions. For example, in case of biased stimuli S 1 with probability and S 2 with probability , we set: Unbiased DD: Biased rewards can be treated similarly, with dependence on D also. Use similar ideas to model social interactions? Simen et al. In preparation, 2007.

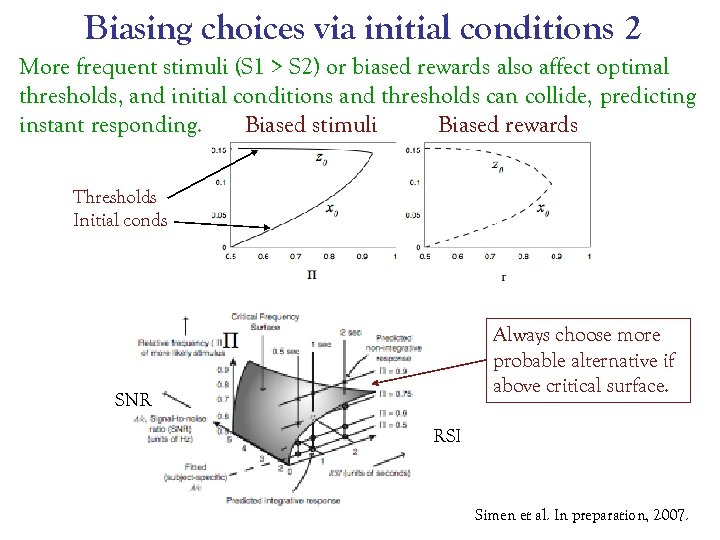Biasing choices via initial conditions 2 More frequent stimuli (S 1 > S 2) or biased rewards also affect optimal thresholds, and initial conditions and thresholds can collide, predicting instant responding. Biased stimuli Biased rewards Thresholds Initial conds Always choose more probable alternative if above critical surface. SNR RSI Simen et al. In preparation, 2007.