65461a33438041b8fc927dcc7bf05f06.ppt
- Количество слайдов: 114
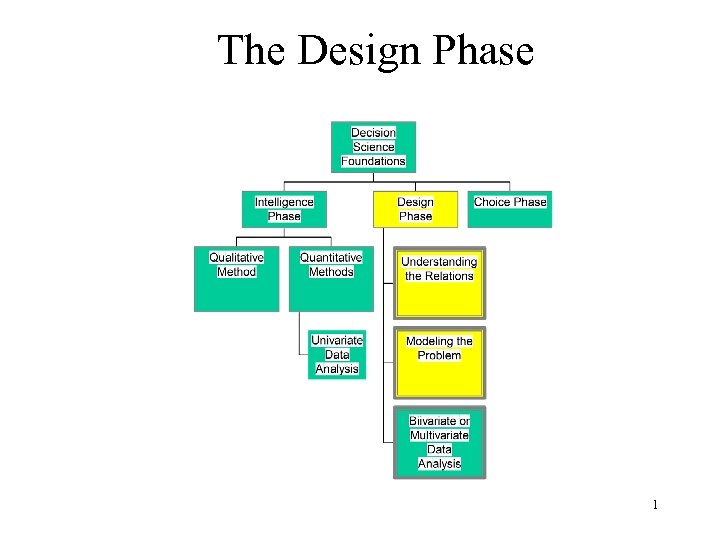 The Design Phase 1
The Design Phase 1
 What Is A Model? • A model is a representation or abstraction of a real-world object, process, concept or “problem” which is reduced in scope or complexity relative to the problem itself but yet retains the certain “essential” aspects which we believe define or characterize the particular real-world problem. • A good model should have a good balance between accuracy and simplicity. 2
What Is A Model? • A model is a representation or abstraction of a real-world object, process, concept or “problem” which is reduced in scope or complexity relative to the problem itself but yet retains the certain “essential” aspects which we believe define or characterize the particular real-world problem. • A good model should have a good balance between accuracy and simplicity. 2
 What Is A Model? • A models may be used to: • describe • predict, or • optimize • Three types of general models • Physical/iconic: model car, model house • Analog/graphic: road map, speedometer • Symbolic: algebraic or spreadsheet model 3
What Is A Model? • A models may be used to: • describe • predict, or • optimize • Three types of general models • Physical/iconic: model car, model house • Analog/graphic: road map, speedometer • Symbolic: algebraic or spreadsheet model 3
 Why Use Models? n. In support of Decision Making and help management make sound decisions n A model is valuable if you make better decisions when you use it (modeling approach) than when you don’t (intuition approach) n. Models + Managerial Judgement = The best way to run business 4
Why Use Models? n. In support of Decision Making and help management make sound decisions n A model is valuable if you make better decisions when you use it (modeling approach) than when you don’t (intuition approach) n. Models + Managerial Judgement = The best way to run business 4
 Advantages of Using Models n Models are generally less expensive and disruptive than experimenting with real systems n Models allow managers to ask “what-if” questions n Models force a consistent and systematic approach to the analysis of problems 5
Advantages of Using Models n Models are generally less expensive and disruptive than experimenting with real systems n Models allow managers to ask “what-if” questions n Models force a consistent and systematic approach to the analysis of problems 5
 Advantages of Using Models “By modeling various alternatives for future system design, Federal Express has, in effect, made its mistakes on paper. Computer modeling works; it allows us to examine many different alternatives and it forces the examination of the entire problem” Fred Smith Chairman and CEO of Fed. Ex 6
Advantages of Using Models “By modeling various alternatives for future system design, Federal Express has, in effect, made its mistakes on paper. Computer modeling works; it allows us to examine many different alternatives and it forces the examination of the entire problem” Fred Smith Chairman and CEO of Fed. Ex 6
 Disadvantages of Models n They may be expensive and time-consuming to develop and test n They are often misused and misunderstood because of their mathematical complexity n They may have assumptions that oversimplify the real-world system 7
Disadvantages of Models n They may be expensive and time-consuming to develop and test n They are often misused and misunderstood because of their mathematical complexity n They may have assumptions that oversimplify the real-world system 7
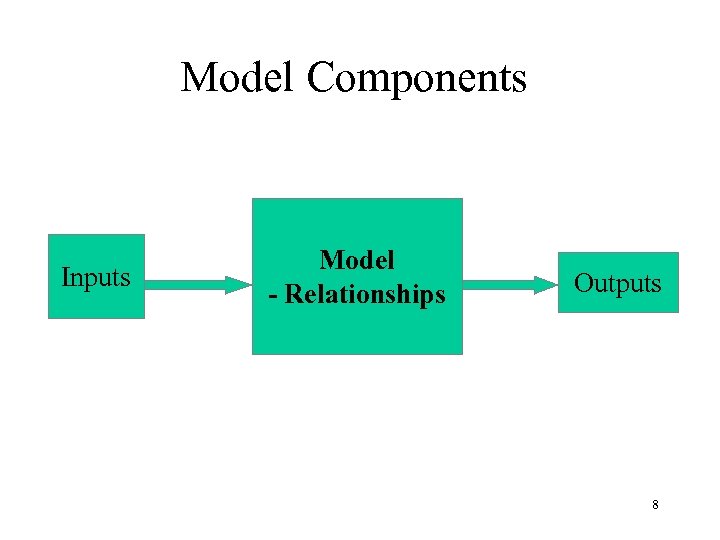 Model Components Inputs Model - Relationships Outputs 8
Model Components Inputs Model - Relationships Outputs 8
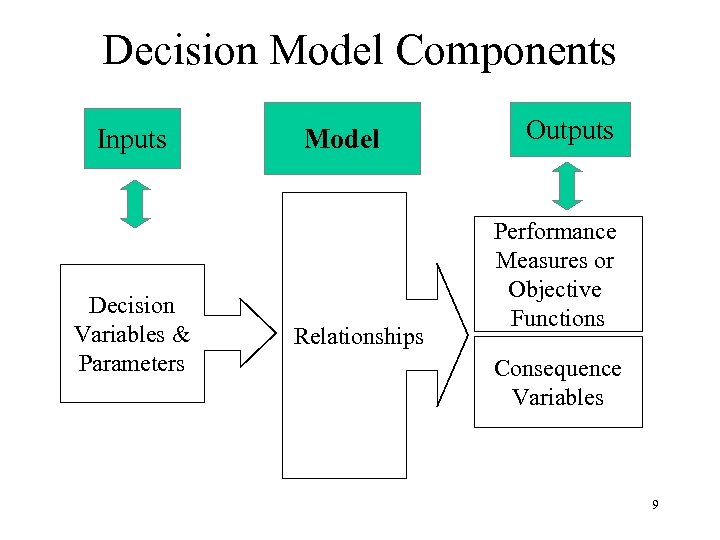 Decision Model Components Inputs Decision Variables & Parameters Model Relationships Outputs Performance Measures or Objective Functions Consequence Variables 9
Decision Model Components Inputs Decision Variables & Parameters Model Relationships Outputs Performance Measures or Objective Functions Consequence Variables 9
 Model and Data n Useful (quantitative) models are developed based on relevant data (numbers); models without data are at best theoretical abstractions n Data are often collected according to the requirements of models – time series vs. cross-sectional – aggregated vs. disaggregated 10
Model and Data n Useful (quantitative) models are developed based on relevant data (numbers); models without data are at best theoretical abstractions n Data are often collected according to the requirements of models – time series vs. cross-sectional – aggregated vs. disaggregated 10
 Numbers in Models n Data – Count – Measure – Rank n Results n Constant n Variable n Coefficient n Precision 11
Numbers in Models n Data – Count – Measure – Rank n Results n Constant n Variable n Coefficient n Precision 11
 Model Classification n Deterministic Models – All model components and relevant data are known with certainty • Examples include: Ad hoc models, Forecasting, Decision analysis, Constrained optimization n Probabilistic (Stochastic) Models – Some components or data are not known with certainty • Examples of include: Monte Carlo simulation, Scheduling and queueing 12
Model Classification n Deterministic Models – All model components and relevant data are known with certainty • Examples include: Ad hoc models, Forecasting, Decision analysis, Constrained optimization n Probabilistic (Stochastic) Models – Some components or data are not known with certainty • Examples of include: Monte Carlo simulation, Scheduling and queueing 12
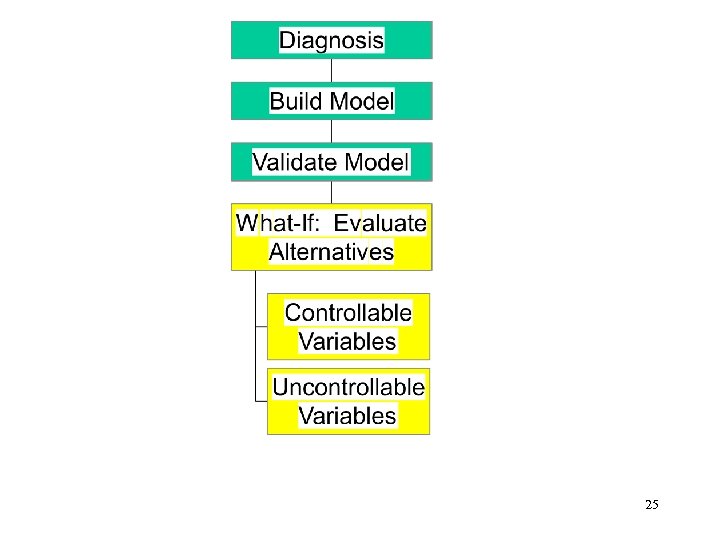
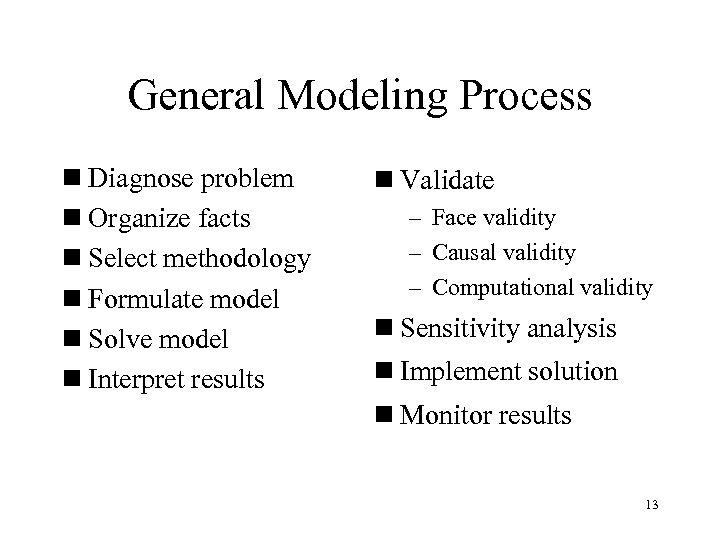 General Modeling Process n Diagnose problem n Organize facts n Select methodology n Formulate model n Solve model n Interpret results n Validate – Face validity – Causal validity – Computational validity n Sensitivity analysis n Implement solution n Monitor results 13
General Modeling Process n Diagnose problem n Organize facts n Select methodology n Formulate model n Solve model n Interpret results n Validate – Face validity – Causal validity – Computational validity n Sensitivity analysis n Implement solution n Monitor results 13
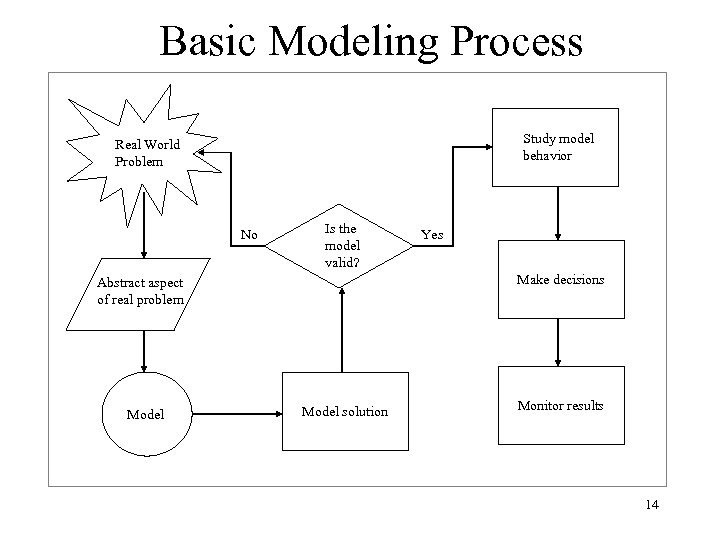 Basic Modeling Process Study model behavior Real World Problem No Is the model valid? Make decisions Abstract aspect of real problem Model Yes Model solution Monitor results 14
Basic Modeling Process Study model behavior Real World Problem No Is the model valid? Make decisions Abstract aspect of real problem Model Yes Model solution Monitor results 14
 Fundamental Relationships n Accounting n Microeconomics n Logic 15
Fundamental Relationships n Accounting n Microeconomics n Logic 15
 Terminology and Relationships n Price n Sales & Production Volume n Supply & Demand n Revenue n Market Share n Contribution n Historical & Replacement Costs n Marking to Market n Allocated Costs n Sunk Costs n Overhead, Fixed & Period Costs n Depreciation and Amortization n Variable or incremental Costs n Capacity n Market Share 16
Terminology and Relationships n Price n Sales & Production Volume n Supply & Demand n Revenue n Market Share n Contribution n Historical & Replacement Costs n Marking to Market n Allocated Costs n Sunk Costs n Overhead, Fixed & Period Costs n Depreciation and Amortization n Variable or incremental Costs n Capacity n Market Share 16
 Model Building: Influence Diagram n A graphical representation (flow chart) of the influencing relationship among variables in a particular problem n Constructing an influence diagram using Top-Down approach – start with output: performance measure – work downward to locate variables that affect the output as well as other variables 17
Model Building: Influence Diagram n A graphical representation (flow chart) of the influencing relationship among variables in a particular problem n Constructing an influence diagram using Top-Down approach – start with output: performance measure – work downward to locate variables that affect the output as well as other variables 17
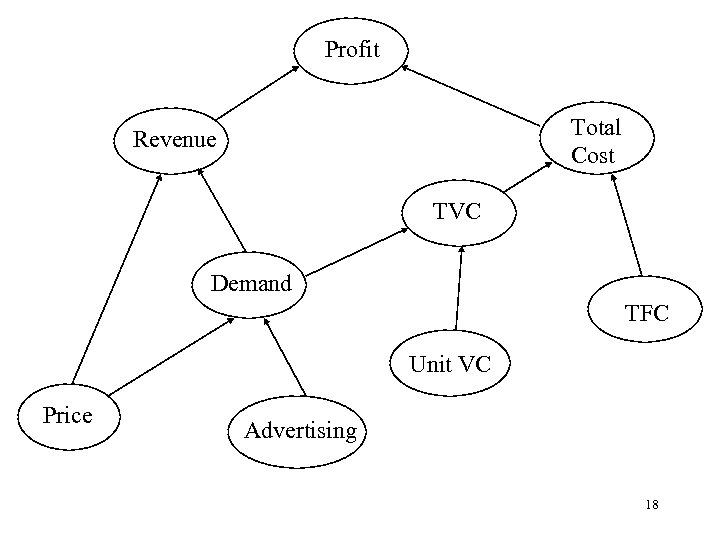 Profit Total Cost Revenue TVC Demand TFC Unit VC Price Advertising 18
Profit Total Cost Revenue TVC Demand TFC Unit VC Price Advertising 18
 Spreadsheet Modeling n Inputs should be logically grouped n Primary outputs should be easy to read n Input and output data should be labeled n Don’t embed parameters in a formula: using cell reference n Use range name n Use fonts and color but don’t overuse them 19
Spreadsheet Modeling n Inputs should be logically grouped n Primary outputs should be easy to read n Input and output data should be labeled n Don’t embed parameters in a formula: using cell reference n Use range name n Use fonts and color but don’t overuse them 19
 20
20
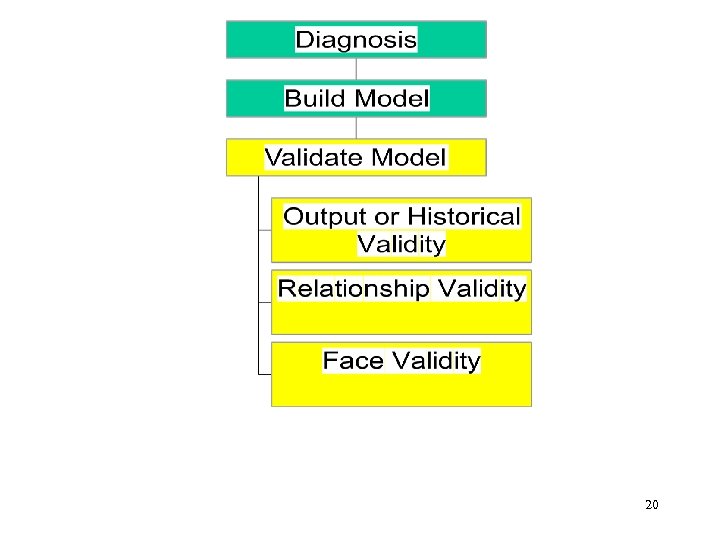
 Validation n A Process of Establishing Confidence that an Inference from Model is Correct. n There is No Single Test for Validity. n Series of Hurdles to Increase Model Builder and User’s Confidence in the Model. 21
Validation n A Process of Establishing Confidence that an Inference from Model is Correct. n There is No Single Test for Validity. n Series of Hurdles to Increase Model Builder and User’s Confidence in the Model. 21
 Face Validity n Is Model’s Output Reasonable? n When Changes Made in Input Variables, Is Value of Output Variable Reasonable? – Be Aware of Counter-Intuitive Model Output! n Enhanced by Using Well-Defined Financial (or Business) Relationships within Model. n Absolute Minimum for Validation. 22
Face Validity n Is Model’s Output Reasonable? n When Changes Made in Input Variables, Is Value of Output Variable Reasonable? – Be Aware of Counter-Intuitive Model Output! n Enhanced by Using Well-Defined Financial (or Business) Relationships within Model. n Absolute Minimum for Validation. 22
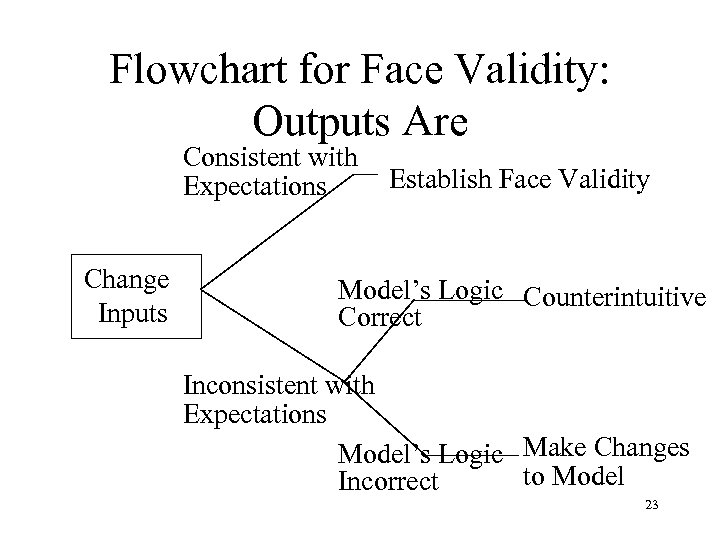 Flowchart for Face Validity: Outputs Are Consistent with Expectations Change Inputs Establish Face Validity Model’s Logic Counterintuitive Correct Inconsistent with Expectations Model’s Logic Make Changes to Model Incorrect 23
Flowchart for Face Validity: Outputs Are Consistent with Expectations Change Inputs Establish Face Validity Model’s Logic Counterintuitive Correct Inconsistent with Expectations Model’s Logic Make Changes to Model Incorrect 23
 Historical & Relational Validity n Compare Model’s Output to Historical Data. n Assess Assumptions About the Relations of the Model Components to Each Other – Builders Must State Assumptions. – Users Must Assess Assumptions. – Must Examine Included and Excluded Assumptions Within the Model. – Review List of Controllable and Uncontrollable Variables and Relevant Ranges. 24
Historical & Relational Validity n Compare Model’s Output to Historical Data. n Assess Assumptions About the Relations of the Model Components to Each Other – Builders Must State Assumptions. – Users Must Assess Assumptions. – Must Examine Included and Excluded Assumptions Within the Model. – Review List of Controllable and Uncontrollable Variables and Relevant Ranges. 24
 25
25
 Optimization n We wish to choose the “best” controllable input based upon the relations and constrains which we can’t control. n We may find this optimum: – Mathematically - using calculus & algebra – Arithmetically - using tables or spreadsheets – Iteratively -using optimization software (I. e. Solver) 26
Optimization n We wish to choose the “best” controllable input based upon the relations and constrains which we can’t control. n We may find this optimum: – Mathematically - using calculus & algebra – Arithmetically - using tables or spreadsheets – Iteratively -using optimization software (I. e. Solver) 26
 Mathematical Optimization n If we have a model which lends itself to a continuous equation, we can use calculus to find a global minimum or maximum. I. e. : – Total Cost = Fixed + Variable Costs • TC = 2000 + 10 * Demand – Demand = 100 – 2 * Price – Profit = TR – TC = P * D – TC n Find the Profit Maximizing Price 27
Mathematical Optimization n If we have a model which lends itself to a continuous equation, we can use calculus to find a global minimum or maximum. I. e. : – Total Cost = Fixed + Variable Costs • TC = 2000 + 10 * Demand – Demand = 100 – 2 * Price – Profit = TR – TC = P * D – TC n Find the Profit Maximizing Price 27
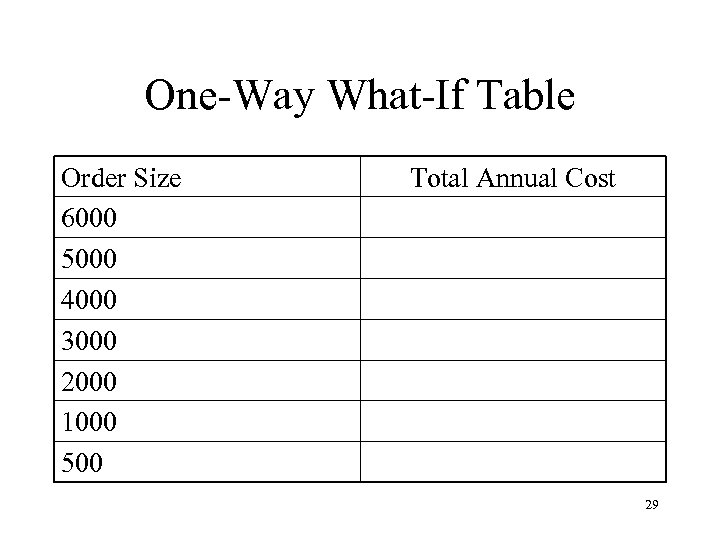
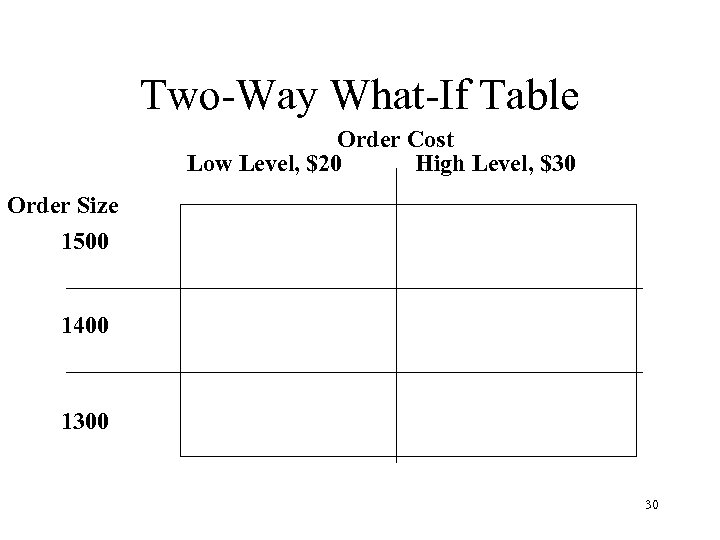
 Arithmetical Optimization n If we don’t have a differentiable equation or a continuous relation but do have a simple equation, we may find an optimum arithmetically using one way or two way tables or spreadsheets. 28
Arithmetical Optimization n If we don’t have a differentiable equation or a continuous relation but do have a simple equation, we may find an optimum arithmetically using one way or two way tables or spreadsheets. 28
 One-Way What-If Table Order Size 6000 5000 4000 3000 2000 1000 500 Total Annual Cost 29
One-Way What-If Table Order Size 6000 5000 4000 3000 2000 1000 500 Total Annual Cost 29
 Two-Way What-If Table Order Cost Low Level, $20 High Level, $30 Order Size 1500 1400 1300 30
Two-Way What-If Table Order Cost Low Level, $20 High Level, $30 Order Size 1500 1400 1300 30
 Iterative Optimization n If we have several controllable variables and/or the variables can take on many different values, we may find an optimum using software which iteratively applies numerical methods such as Excel’s Solver. n Since this is numerical (and not mathematical), we cannot be assured that we have found a truly global optimum but instead may have found a local one. 31
Iterative Optimization n If we have several controllable variables and/or the variables can take on many different values, we may find an optimum using software which iteratively applies numerical methods such as Excel’s Solver. n Since this is numerical (and not mathematical), we cannot be assured that we have found a truly global optimum but instead may have found a local one. 31
 Hill Climbing 32
Hill Climbing 32
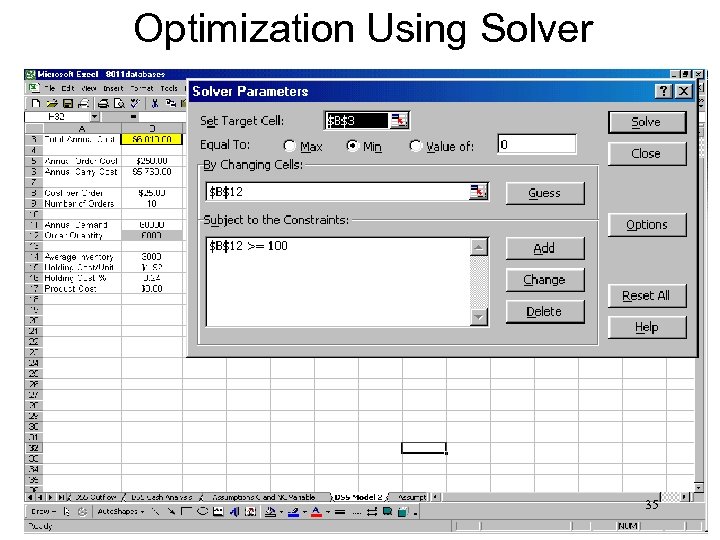
 Using Excel’s Solver for Optimization n Answers Questions Such As: – What Order Size Will Minimize Total Annual Cost? – How Much Should I Invest in Stock 1 to Maximize Portfolio Return? n Output (AKA Target) Cell is Cell Whose Target Value You Wish to Maximize or Minimize. 33
Using Excel’s Solver for Optimization n Answers Questions Such As: – What Order Size Will Minimize Total Annual Cost? – How Much Should I Invest in Stock 1 to Maximize Portfolio Return? n Output (AKA Target) Cell is Cell Whose Target Value You Wish to Maximize or Minimize. 33
 Using Excel’s Solver n Input Variables or Changing Cells Are Those Cells Whose Values Are Adjusted Until a Solution is Found. n Constraint – The Range of Permissible Values for the Controllable Variables. n Uses an Iterative Procedure to Found the Peak or Valley for the Target Variable. 34
Using Excel’s Solver n Input Variables or Changing Cells Are Those Cells Whose Values Are Adjusted Until a Solution is Found. n Constraint – The Range of Permissible Values for the Controllable Variables. n Uses an Iterative Procedure to Found the Peak or Valley for the Target Variable. 34
 Optimization Using Solver 35
Optimization Using Solver 35
 Problem Using Excel’s Solver n Problem: Solver Sometimes Find a Local Maximum (Hill Top) and Not the Global Maximum (Mountain Top). n Solution: Try Running Solver Several Times with Different Starting Values in the Changing Cells (Base Camps). 36
Problem Using Excel’s Solver n Problem: Solver Sometimes Find a Local Maximum (Hill Top) and Not the Global Maximum (Mountain Top). n Solution: Try Running Solver Several Times with Different Starting Values in the Changing Cells (Base Camps). 36
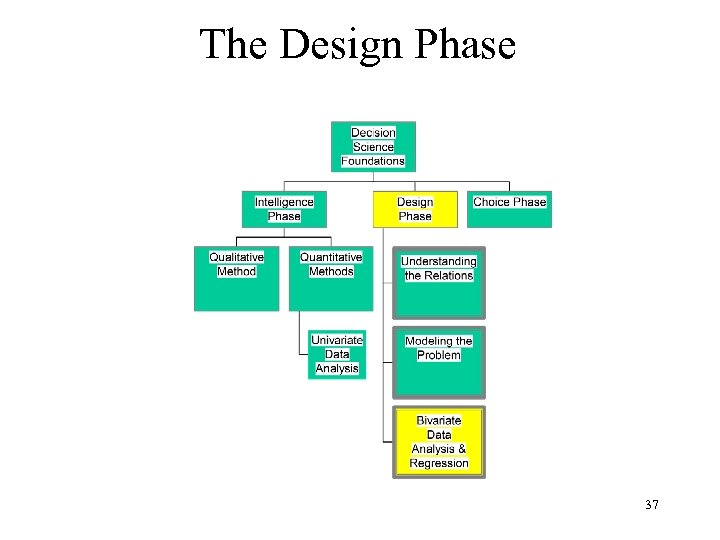 The Design Phase 37
The Design Phase 37
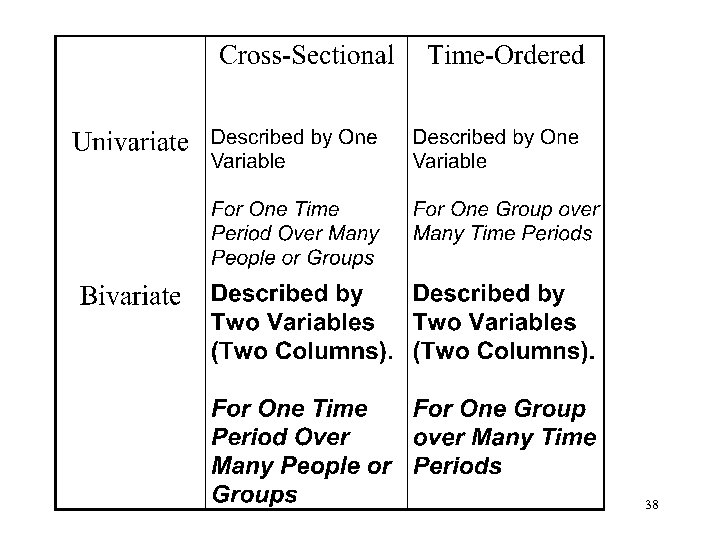 38
38
 Overview of Bivariate Data: Looking For Relationships Analyzing Specific Data 39
Overview of Bivariate Data: Looking For Relationships Analyzing Specific Data 39
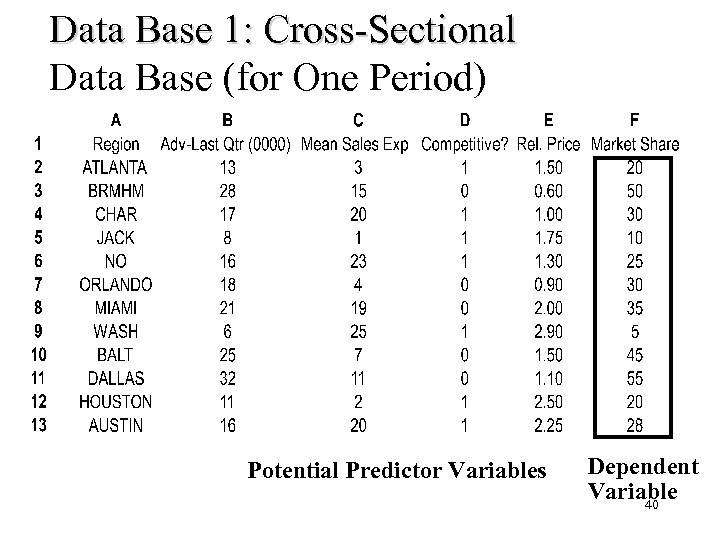 Data Base 1: Cross-Sectional Data Base (for One Period) Potential Predictor Variables Dependent Variable 40
Data Base 1: Cross-Sectional Data Base (for One Period) Potential Predictor Variables Dependent Variable 40
 Does Market Share Data Exhibit Much Variation (Data Base 1)? n Compute Coefficient of Variation (CV). n If CV Greater Than 25 -30%, Generate Possible Predictor Variables That Might Affect the Dependent Variable, Market Share. 41
Does Market Share Data Exhibit Much Variation (Data Base 1)? n Compute Coefficient of Variation (CV). n If CV Greater Than 25 -30%, Generate Possible Predictor Variables That Might Affect the Dependent Variable, Market Share. 41
 Types of Variables n Dependent Variable is the Variable You Wish to Understand or Predict. n Predictor, or Independent, Variables Are the Predictor Independent Variables You Believe Affect the Dependent Variable. 42
Types of Variables n Dependent Variable is the Variable You Wish to Understand or Predict. n Predictor, or Independent, Variables Are the Predictor Independent Variables You Believe Affect the Dependent Variable. 42
 Correlation n If two variables are related to each other, then changes in one can be related to changes in the other. In other words, they rise and/or fall together. n Measured by a coefficient -1 £ r £ 1. n One variable may be caused by the other OR they both may be caused by other causes (intervening variables). 43
Correlation n If two variables are related to each other, then changes in one can be related to changes in the other. In other words, they rise and/or fall together. n Measured by a coefficient -1 £ r £ 1. n One variable may be caused by the other OR they both may be caused by other causes (intervening variables). 43
 Causal Models n Causal Models - where we have one numerical dependent variable and one or more independent variables which we say “cause” the dependent variable – Salary is “caused by” gender and months on the job. – Wrecks are “caused by” alcohol, cell phones, speed, etc. – Advertising “causes” sales. 44
Causal Models n Causal Models - where we have one numerical dependent variable and one or more independent variables which we say “cause” the dependent variable – Salary is “caused by” gender and months on the job. – Wrecks are “caused by” alcohol, cell phones, speed, etc. – Advertising “causes” sales. 44
 Establishing Causality n. Necessary (but not sufficient) determinates of Causality: – Correlation - variables rise and/or fall together. – Temporal precedence - cause precedes effect in time. – Logical mechanism - must have reasonable explanation of how independent variable causes the dependent variable to vary. 45
Establishing Causality n. Necessary (but not sufficient) determinates of Causality: – Correlation - variables rise and/or fall together. – Temporal precedence - cause precedes effect in time. – Logical mechanism - must have reasonable explanation of how independent variable causes the dependent variable to vary. 45
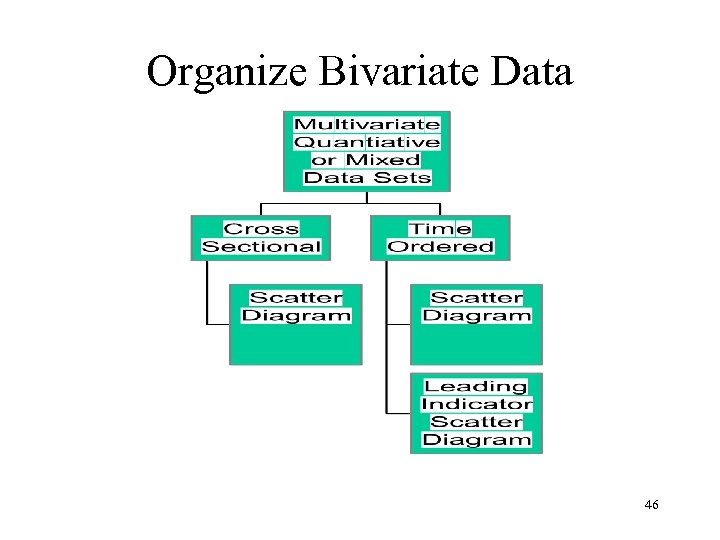 Organize Bivariate Data 46
Organize Bivariate Data 46
 Slide 2 47
Slide 2 47
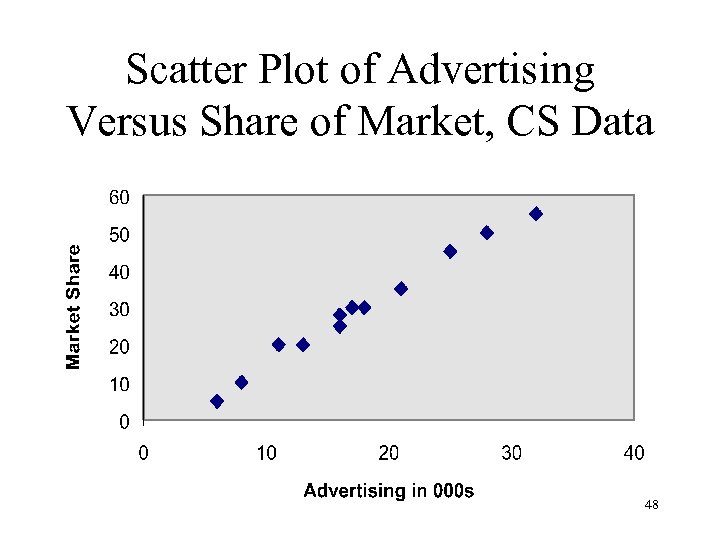 Scatter Plot of Advertising Versus Share of Market, CS Data 48
Scatter Plot of Advertising Versus Share of Market, CS Data 48
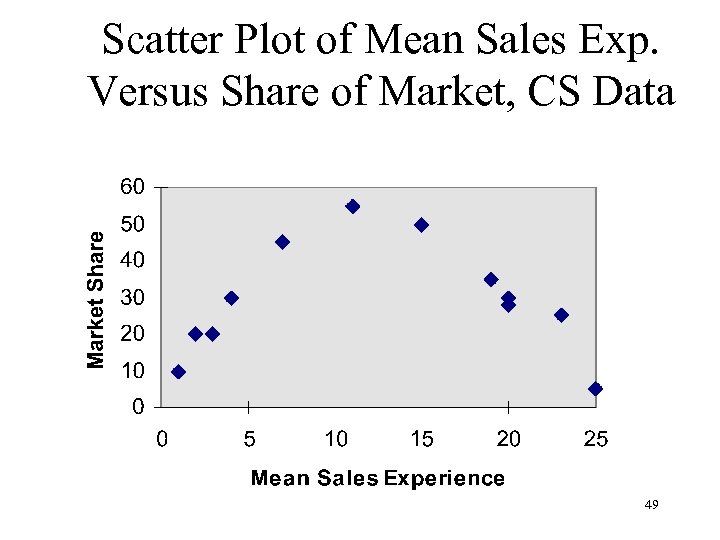 Scatter Plot of Mean Sales Exp. Versus Share of Market, CS Data 49
Scatter Plot of Mean Sales Exp. Versus Share of Market, CS Data 49
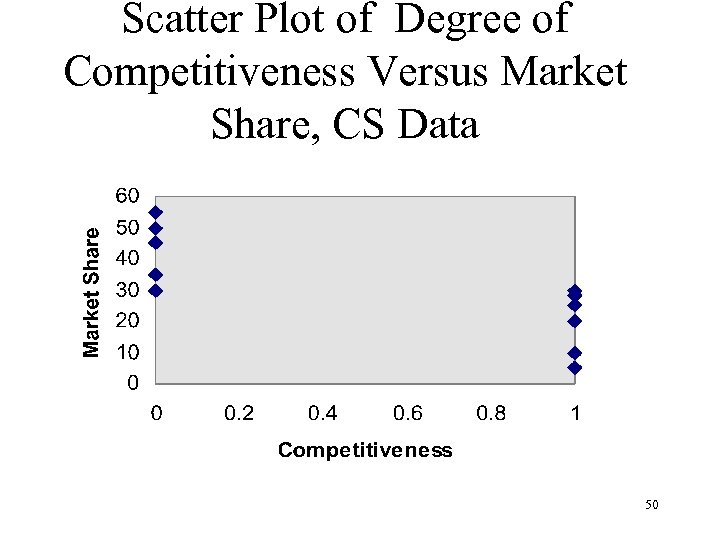 Scatter Plot of Degree of Competitiveness Versus Market Share, CS Data 50
Scatter Plot of Degree of Competitiveness Versus Market Share, CS Data 50
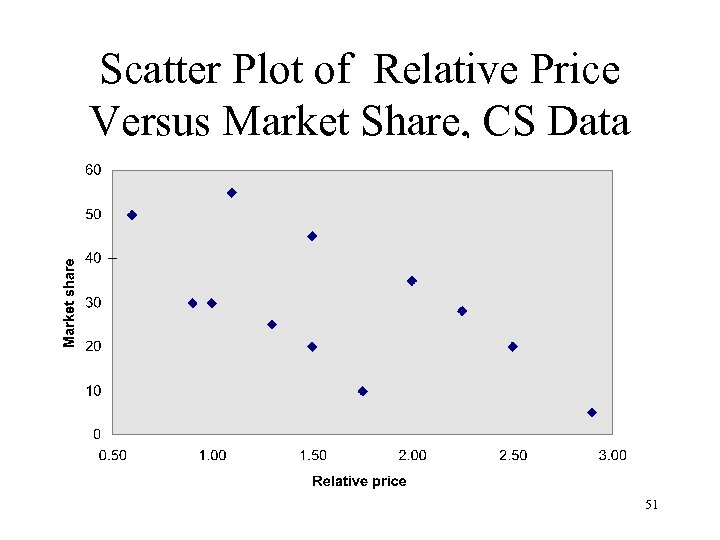 Scatter Plot of Relative Price Versus Market Share, CS Data 51
Scatter Plot of Relative Price Versus Market Share, CS Data 51
 Leading Predictor Variables n Does ADV (t) Affect Sales (t)? n Since the Cause proceeds the Effect in time, if we are using time-ordered data, we may need to have the effect lag the cause in time. n If advertising causes sales, does this months advertising effect this months sales or next months sales? 52
Leading Predictor Variables n Does ADV (t) Affect Sales (t)? n Since the Cause proceeds the Effect in time, if we are using time-ordered data, we may need to have the effect lag the cause in time. n If advertising causes sales, does this months advertising effect this months sales or next months sales? 52
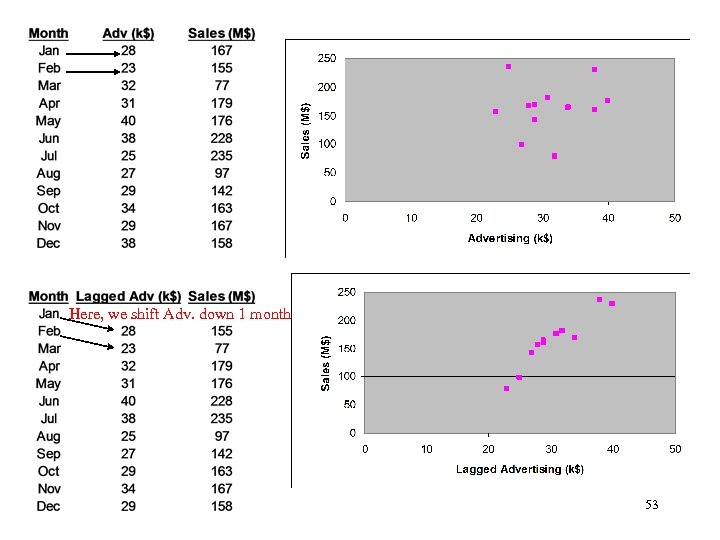 Here, we shift Adv. down 1 month 53
Here, we shift Adv. down 1 month 53
 Overview of Bivariate Data Looking For Relationships Analyzing Specific Data 54
Overview of Bivariate Data Looking For Relationships Analyzing Specific Data 54
 Equation for a Line b is the _______ m is the _______ 55
Equation for a Line b is the _______ m is the _______ 55
 Intercept and Slope n The intercept is: n The slope is: 56
Intercept and Slope n The intercept is: n The slope is: 56
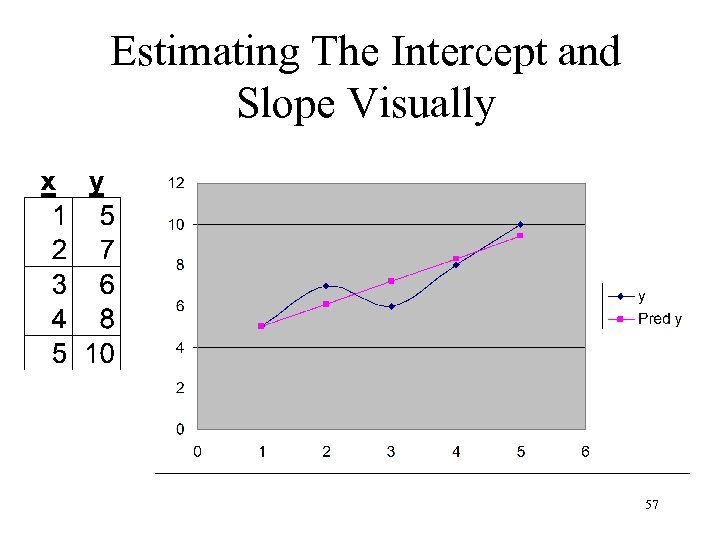 Estimating The Intercept and Slope Visually 57
Estimating The Intercept and Slope Visually 57
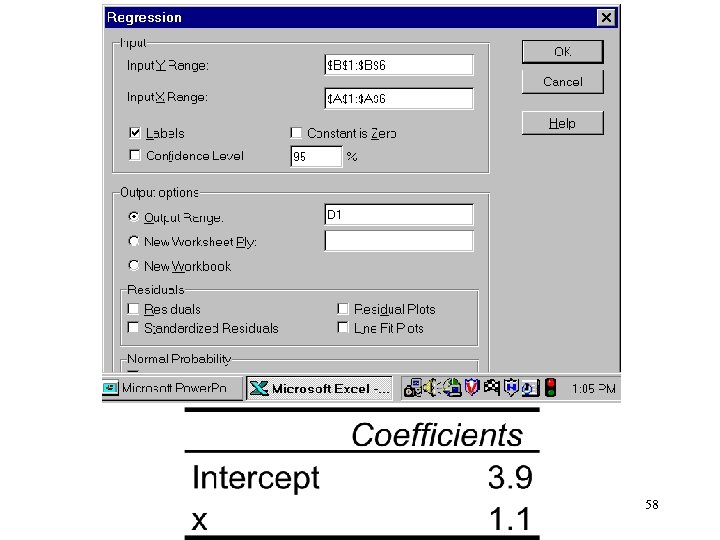 58
58
 Overview of Bivariate Data Looking For Relationships Analyzing Specific Data 59
Overview of Bivariate Data Looking For Relationships Analyzing Specific Data 59
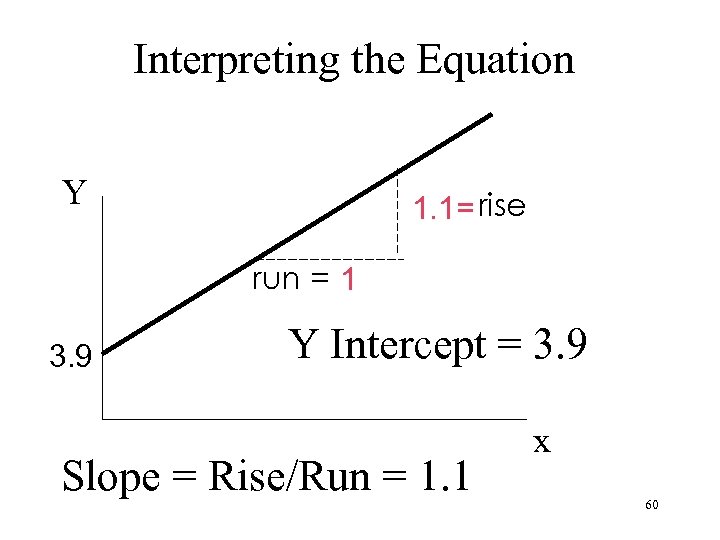 Interpreting the Equation Y 1. 1= rise run = 1 3. 9 Y Intercept = 3. 9 Slope = Rise/Run = 1. 1 x 60
Interpreting the Equation Y 1. 1= rise run = 1 3. 9 Y Intercept = 3. 9 Slope = Rise/Run = 1. 1 x 60
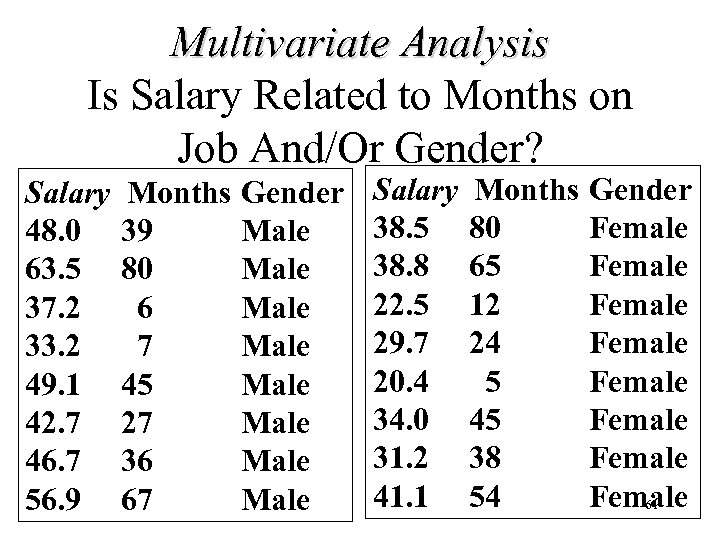 Multivariate Analysis Is Salary Related to Months on Job And/Or Gender? Salary 48. 0 63. 5 37. 2 33. 2 49. 1 42. 7 46. 7 56. 9 Months 39 80 6 7 45 27 36 67 Gender Male Male Salary 38. 5 38. 8 22. 5 29. 7 20. 4 34. 0 31. 2 41. 1 Months 80 65 12 24 5 45 38 54 Gender Female Female 61
Multivariate Analysis Is Salary Related to Months on Job And/Or Gender? Salary 48. 0 63. 5 37. 2 33. 2 49. 1 42. 7 46. 7 56. 9 Months 39 80 6 7 45 27 36 67 Gender Male Male Salary 38. 5 38. 8 22. 5 29. 7 20. 4 34. 0 31. 2 41. 1 Months 80 65 12 24 5 45 38 54 Gender Female Female 61
 Lecture Flow 62
Lecture Flow 62
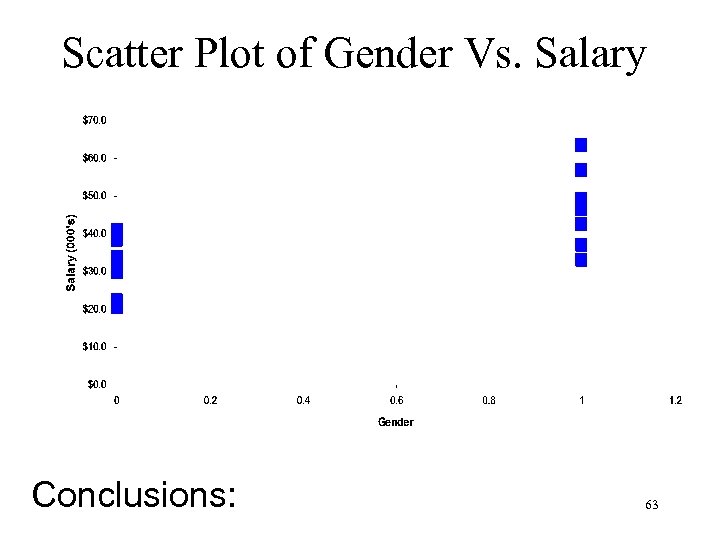 Scatter Plot of Gender Vs. Salary Conclusions: 63
Scatter Plot of Gender Vs. Salary Conclusions: 63
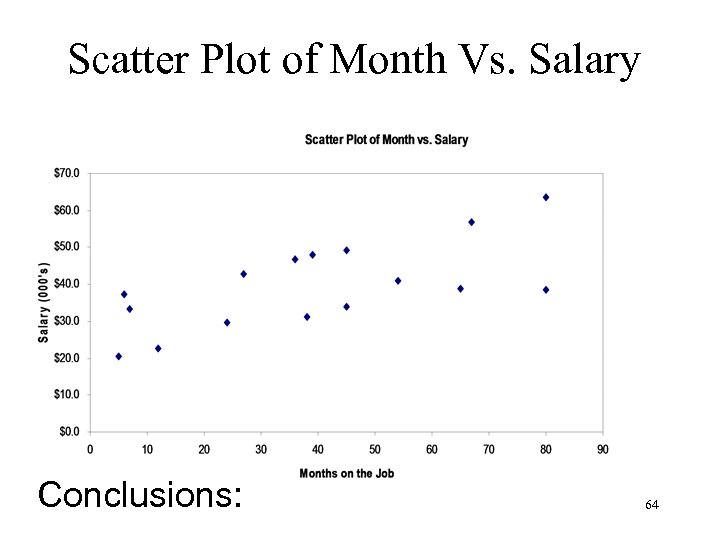 Scatter Plot of Month Vs. Salary Conclusions: 64
Scatter Plot of Month Vs. Salary Conclusions: 64
 Purposes of Scatter Plots n Does a relation appears to exist? n If so, is the relation negative or positive? n What shape is the relation? – If linear, we can apply linear regression. – If non-linear, we may apply a linear transformation before using regression (subjects of DSc 3120 and beyond). 65
Purposes of Scatter Plots n Does a relation appears to exist? n If so, is the relation negative or positive? n What shape is the relation? – If linear, we can apply linear regression. – If non-linear, we may apply a linear transformation before using regression (subjects of DSc 3120 and beyond). 65
 Lecture Flow 66
Lecture Flow 66
 Interpreting Regression Model or Equation n Holding Gender Constant, For Every Additional Month on Job, Salary, On Average, Increases by ____Thousands of Dollars or $______. n Holding Gender Constant, For Every Additional 10 Months on Job, Salary, On Average, Increases by ____Thousands of Dollars or $______. 67
Interpreting Regression Model or Equation n Holding Gender Constant, For Every Additional Month on Job, Salary, On Average, Increases by ____Thousands of Dollars or $______. n Holding Gender Constant, For Every Additional 10 Months on Job, Salary, On Average, Increases by ____Thousands of Dollars or $______. 67
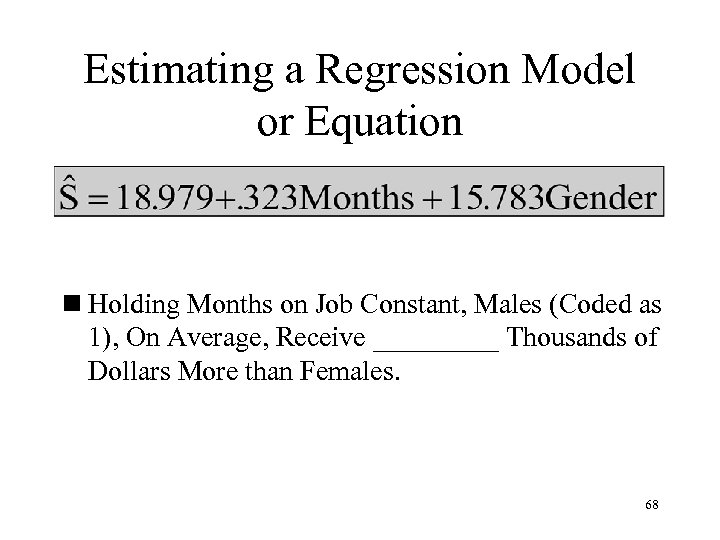 Estimating a Regression Model or Equation n Holding Months on Job Constant, Males (Coded as 1), On Average, Receive _____ Thousands of Dollars More than Females. 68
Estimating a Regression Model or Equation n Holding Months on Job Constant, Males (Coded as 1), On Average, Receive _____ Thousands of Dollars More than Females. 68
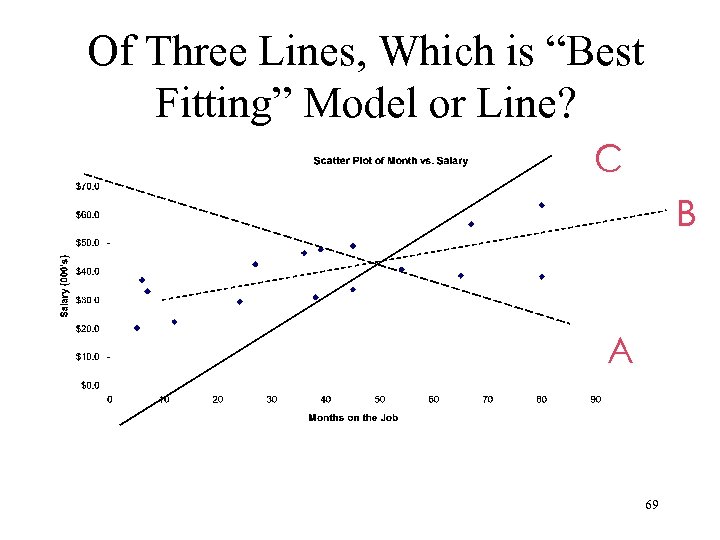 Of Three Lines, Which is “Best Fitting” Model or Line? C B A 69
Of Three Lines, Which is “Best Fitting” Model or Line? C B A 69
 A “Best-Fitting” Line: n embodies the underlying trend of the data, n comes closest to all data points (I. e. misses all the points by the least total distances), therefore it is the line which: n minimizes the sum of squared deviations or errors (this method is known as the method of “Least Squared Errors” or LSE or OLS or MLS) 70
A “Best-Fitting” Line: n embodies the underlying trend of the data, n comes closest to all data points (I. e. misses all the points by the least total distances), therefore it is the line which: n minimizes the sum of squared deviations or errors (this method is known as the method of “Least Squared Errors” or LSE or OLS or MLS) 70
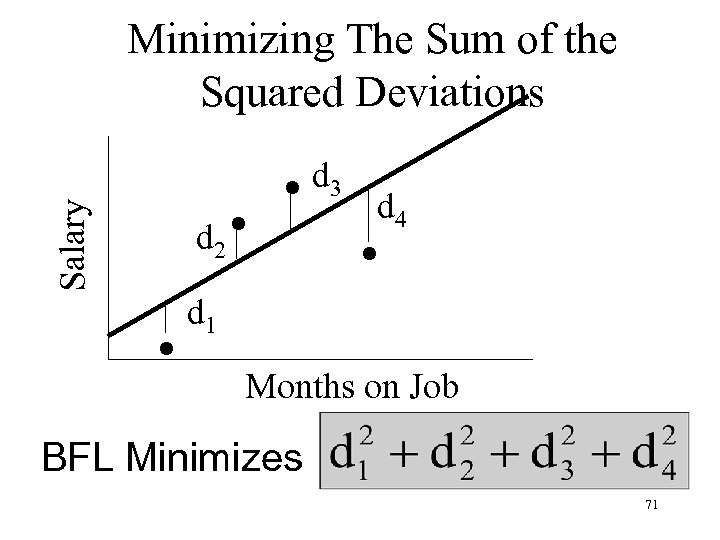 Salary Minimizing The Sum of the Squared Deviations . . . d 2 d 3 . d 4 d 1 Months on Job BFL Minimizes 71
Salary Minimizing The Sum of the Squared Deviations . . . d 2 d 3 . d 4 d 1 Months on Job BFL Minimizes 71
 How to Determine Line that Minimizes n Trial and error n Special software n Least Squares Equation (Developed from Calculus) Slope Intercept 72
How to Determine Line that Minimizes n Trial and error n Special software n Least Squares Equation (Developed from Calculus) Slope Intercept 72
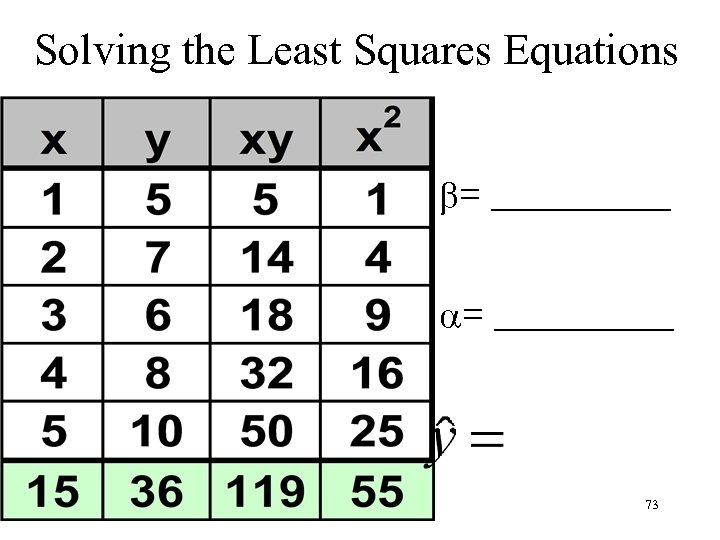 Solving the Least Squares Equations = __________ 73
Solving the Least Squares Equations = __________ 73
 Generating the Best Fitting Model in Practice n Don’t Solve LSE by Hand. n Use Software that Solves LSE. n For Salary Study, the Best Fitting Model is: 74
Generating the Best Fitting Model in Practice n Don’t Solve LSE by Hand. n Use Software that Solves LSE. n For Salary Study, the Best Fitting Model is: 74
 Lecture Flow If Not Significant, Seek Additional Predictor Variables 75
Lecture Flow If Not Significant, Seek Additional Predictor Variables 75
 How Much Variation (Sum of Squares) Is There in Dependent Salary Variable? ? 48. 0 63. 5 37. 2 33. 2 49. 1 42. 7 46. 7 56. 9 38. 5 38. 8 22. 5 29. 7 20. 4 34. 0 31. 2 41. 1 SST = ( ( )2 +. . . + )2 2003. 129 76
How Much Variation (Sum of Squares) Is There in Dependent Salary Variable? ? 48. 0 63. 5 37. 2 33. 2 49. 1 42. 7 46. 7 56. 9 38. 5 38. 8 22. 5 29. 7 20. 4 34. 0 31. 2 41. 1 SST = ( ( )2 +. . . + )2 2003. 129 76
 What Is SST Due To? ? 2003. 129 The Variation in the Dependent Variable is based the factors in our model plus all factors not in our model: SSTotal = SSRegression + SSErrors 1906. 042 97. 087 + All Other Factors 77 Two Factors
What Is SST Due To? ? 2003. 129 The Variation in the Dependent Variable is based the factors in our model plus all factors not in our model: SSTotal = SSRegression + SSErrors 1906. 042 97. 087 + All Other Factors 77 Two Factors
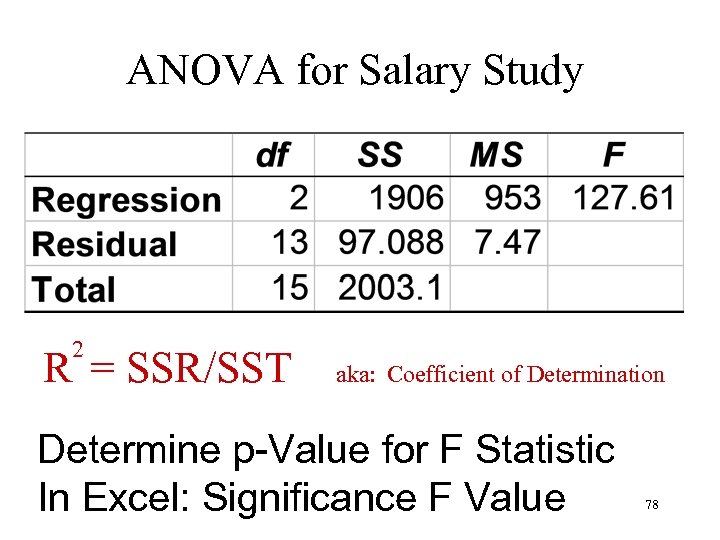 ANOVA for Salary Study 2 R = SSR/SST aka: Coefficient of Determination Determine p-Value for F Statistic In Excel: Significance F Value 78
ANOVA for Salary Study 2 R = SSR/SST aka: Coefficient of Determination Determine p-Value for F Statistic In Excel: Significance F Value 78
 The Standard Error of the Estimate, SY|X n The Standard Error of the Estimate Measures Impact of All Factors (Other than Months on Job and Gender) On Salary. n Equals and is $2. 733 ($2, 733) for Salary Study. n If Only Months on Job and Gender Affected Salary, s. Y|X Would Equal 79
The Standard Error of the Estimate, SY|X n The Standard Error of the Estimate Measures Impact of All Factors (Other than Months on Job and Gender) On Salary. n Equals and is $2. 733 ($2, 733) for Salary Study. n If Only Months on Job and Gender Affected Salary, s. Y|X Would Equal 79
 Why Reduce Standard Error of the Estimate n Will Use Standard Error for Making Salary Predictions Using Regression Model. n Salary of Male (1) with 10 Months? ? n$ + MOE n Size of MOE Depends, in Part, on Standard Error of Estimate. 80
Why Reduce Standard Error of the Estimate n Will Use Standard Error for Making Salary Predictions Using Regression Model. n Salary of Male (1) with 10 Months? ? n$ + MOE n Size of MOE Depends, in Part, on Standard Error of Estimate. 80
 How to Reduce Standard Error? n Increase sample size. n Eliminate “weak” predictor variables through t-value screening. 81
How to Reduce Standard Error? n Increase sample size. n Eliminate “weak” predictor variables through t-value screening. 81
 Lecture Flow If Overall Model Sig, then: 82
Lecture Flow If Overall Model Sig, then: 82
 t-Value Screening Procedure to Reduce Standard Error of Estimate 1 Take the Absolute Value of the t. Values for Predictor Variables from Parameter Estimate Section. 2 Delete Predictor Variable if Smallest t-Value Less Than 2. 0 3 Use Software to Re-estimate Model. 4 Repeat Steps 1 -3 As Necessary. 83
t-Value Screening Procedure to Reduce Standard Error of Estimate 1 Take the Absolute Value of the t. Values for Predictor Variables from Parameter Estimate Section. 2 Delete Predictor Variable if Smallest t-Value Less Than 2. 0 3 Use Software to Re-estimate Model. 4 Repeat Steps 1 -3 As Necessary. 83
 Lecture Flow 84
Lecture Flow 84
 Interpolation vs. Extrapolation n Interpolation: Predict Values of y Within Range of Study’s Predictor Variables. – Range of Months on Job is From ____ to ______. n Extrapolation: Predict Values of y Outside Range of Study’s Predictor Variables. n Extrapolate Only When You Believe Regression Model Is Valid Outside Range of Data. 85
Interpolation vs. Extrapolation n Interpolation: Predict Values of y Within Range of Study’s Predictor Variables. – Range of Months on Job is From ____ to ______. n Extrapolation: Predict Values of y Outside Range of Study’s Predictor Variables. n Extrapolate Only When You Believe Regression Model Is Valid Outside Range of Data. 85
 Making Predictions using Prediction and Confidence Intervals n. Confidence Intervals: Prediction on Mean Salary for Group of People. n. Prediction Intervals: Prediction on Expected Salary for a Single Person. 86
Making Predictions using Prediction and Confidence Intervals n. Confidence Intervals: Prediction on Mean Salary for Group of People. n. Prediction Intervals: Prediction on Expected Salary for a Single Person. 86
 Making Predictions for Persons with 50 Months on Job For a Male with 50 Months on Job $50, 912 + MOE For a Female with 50 Months $35, 129 + MOE 87
Making Predictions for Persons with 50 Months on Job For a Male with 50 Months on Job $50, 912 + MOE For a Female with 50 Months $35, 129 + MOE 87
 Making Approximate Salary Predictions for Male with 50 Months on Job n For One Male n Average of All Males 88
Making Approximate Salary Predictions for Male with 50 Months on Job n For One Male n Average of All Males 88
 Reducing the Width of Confidence Interval and MOE n Remove Predictor Variables from Model with |t| Values < 2 (Screening Procedure). This reduces the Standard Error. n Increase sample size - reduces the Standard Error. n Accepting lower level of confidence (I. e. smaller t) - reduces Confidence Coefficient. 89
Reducing the Width of Confidence Interval and MOE n Remove Predictor Variables from Model with |t| Values < 2 (Screening Procedure). This reduces the Standard Error. n Increase sample size - reduces the Standard Error. n Accepting lower level of confidence (I. e. smaller t) - reduces Confidence Coefficient. 89
 Summary of Regression n Regression Analysis Looks for Relations between variables. n What is the business application for regression? 90
Summary of Regression n Regression Analysis Looks for Relations between variables. n What is the business application for regression? 90
 Forecasting Time Series Models 91
Forecasting Time Series Models 91
 Forecasting Models n Budgets n Sales quotas n Financial pro-formas Time series models Causal models Qualitative models 92
Forecasting Models n Budgets n Sales quotas n Financial pro-formas Time series models Causal models Qualitative models 92
 Causal Models vs. Time Series Models n Time as a surrogate for causal factors n Relate patterns in dependent variables to the passage of time n Stationary Time Series Assumption – Data will continue to operate in the (near) future as it has in the (recent) past. 93
Causal Models vs. Time Series Models n Time as a surrogate for causal factors n Relate patterns in dependent variables to the passage of time n Stationary Time Series Assumption – Data will continue to operate in the (near) future as it has in the (recent) past. 93
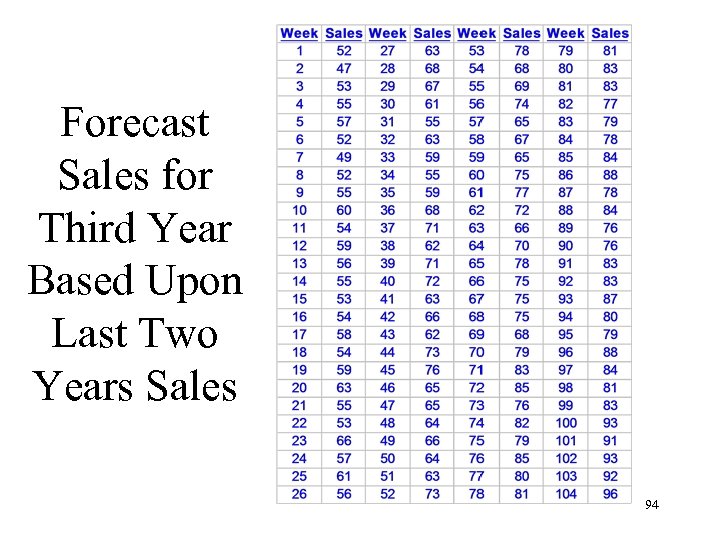 Forecast Sales for Third Year Based Upon Last Two Years Sales 94
Forecast Sales for Third Year Based Upon Last Two Years Sales 94
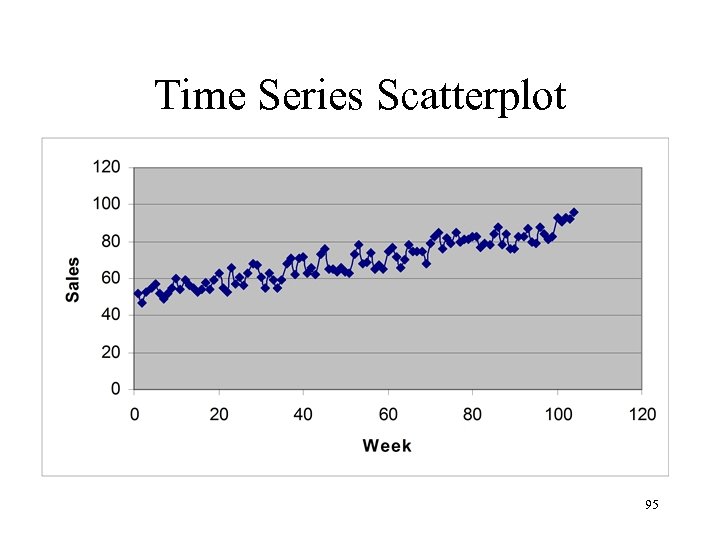 Time Series Scatterplot 95
Time Series Scatterplot 95
 Naïve Model n Whatever happened recently will happen again this time. n The model is simple and flexible. n Provides a baseline against which to evaluate other models. 96
Naïve Model n Whatever happened recently will happen again this time. n The model is simple and flexible. n Provides a baseline against which to evaluate other models. 96
 Exponential Smoothing Models n Advantages – Requires little data – Quick and simple to compute – Emphasizes the most up-to-date data – Cheap – Suitable for highvolume forecasts n Disadvantages – Simple ES always lags trend in the data – Double ES ignores seasonality – Winter’s method is complex 97
Exponential Smoothing Models n Advantages – Requires little data – Quick and simple to compute – Emphasizes the most up-to-date data – Cheap – Suitable for highvolume forecasts n Disadvantages – Simple ES always lags trend in the data – Double ES ignores seasonality – Winter’s method is complex 97
 Simple Exponential Smoothing n n Ft-1 n Yt-1 n Forecast for period t Most recent forecast Most recent actual data point Smoothing constant ( 0 < < 1 ) 98
Simple Exponential Smoothing n n Ft-1 n Yt-1 n Forecast for period t Most recent forecast Most recent actual data point Smoothing constant ( 0 < < 1 ) 98
 Double Exponential Smoothing n Ft n Ct n Tt n Yt-1 n n Forecast for period t Continuously updated intercept Smoothed period to period slope Most recent actual observed value Smoothing constant for intercept C Smoothing constant for trend T 99
Double Exponential Smoothing n Ft n Ct n Tt n Yt-1 n n Forecast for period t Continuously updated intercept Smoothed period to period slope Most recent actual observed value Smoothing constant for intercept C Smoothing constant for trend T 99
 Winter’s Method n Adds a third smoothing constant n Adds smoothed Seasonal Indices n Much more complex than exponential smoothing 100
Winter’s Method n Adds a third smoothing constant n Adds smoothed Seasonal Indices n Much more complex than exponential smoothing 100
 Measuring Error n Bias - The arithmetic mean of the errors n Mean Square Error - Similar to simple sample variance n Variance - Population variance (adjusted for degrees of freedom) n Standard Error - Standard deviation of the sampling distribution n MAD - Mean Absolute Deviation 101
Measuring Error n Bias - The arithmetic mean of the errors n Mean Square Error - Similar to simple sample variance n Variance - Population variance (adjusted for degrees of freedom) n Standard Error - Standard deviation of the sampling distribution n MAD - Mean Absolute Deviation 101
 Classical Time Series Conceptual Model • Y 1 - The original data representing activity in time period t • Trend - The time pattern of the basic level of the data • Cyclical - Long term swings above and below the trend level • Seasonal - A cycle that has a period of exactly one year for a complete cycle • Error - The underlying degree of randomness or error in model 102
Classical Time Series Conceptual Model • Y 1 - The original data representing activity in time period t • Trend - The time pattern of the basic level of the data • Cyclical - Long term swings above and below the trend level • Seasonal - A cycle that has a period of exactly one year for a complete cycle • Error - The underlying degree of randomness or error in model 102
 Trend Models n Rather than working month to month, why not fit a line through the historical data and project it into the future? n The mathematical method for calculating the best curve is called the “method of least squares. ” – Minimize E(Y - a - b. X)2 with respect to our choice of a and b 103
Trend Models n Rather than working month to month, why not fit a line through the historical data and project it into the future? n The mathematical method for calculating the best curve is called the “method of least squares. ” – Minimize E(Y - a - b. X)2 with respect to our choice of a and b 103
 Trend Models n Pros Can predict into the future – Formalizes a method to minimize error term – Can use a number of curve forms – n Cons – Ignores seasonal changes 104
Trend Models n Pros Can predict into the future – Formalizes a method to minimize error term – Can use a number of curve forms – n Cons – Ignores seasonal changes 104
 Time Series Decomposition n The conceptual forecasting model is: – Y = Trend x Cyclical x Seasonal x Error n Since we cannot easily extract or predict cycles, we will assume that the trend component will capture cycles during the forecast period n Since we must live with error (we cannot predict it) our model is simplified to: – Y = Trend x Seasonal 105
Time Series Decomposition n The conceptual forecasting model is: – Y = Trend x Cyclical x Seasonal x Error n Since we cannot easily extract or predict cycles, we will assume that the trend component will capture cycles during the forecast period n Since we must live with error (we cannot predict it) our model is simplified to: – Y = Trend x Seasonal 105
 Estimating Trend n Since we cannot solve for two unknowns using one equation, we must first estimate one of our values n The best estimate to work with in this case is the One Year Centered Moving Average – The advantage of CMA is that it makes no assumptions about the underlying data and completely averages out seasonality 106
Estimating Trend n Since we cannot solve for two unknowns using one equation, we must first estimate one of our values n The best estimate to work with in this case is the One Year Centered Moving Average – The advantage of CMA is that it makes no assumptions about the underlying data and completely averages out seasonality 106
 Centered Moving Average n Starting with the first datum, we average one year’s worth of observations placing the result at the center point n We continue by moving to the next datum and repeating the process until we no longer have a complete year to average 107
Centered Moving Average n Starting with the first datum, we average one year’s worth of observations placing the result at the center point n We continue by moving to the next datum and repeating the process until we no longer have a complete year to average 107
 Centered Moving Average n The initial average lies between the middle values (quarters or months) n To get the centered moving average, we average the two values on either side to get the CMA n NOTE: In averaging one year of data, we lose the first and last six months 108
Centered Moving Average n The initial average lies between the middle values (quarters or months) n To get the centered moving average, we average the two values on either side to get the CMA n NOTE: In averaging one year of data, we lose the first and last six months 108
 Raw Seasonal Ratios n Now that we have an estimate for trend, we can solve our general model for seasonality – Season = Y / Trend n We use this formula to calculate the Raw Seasonal Ratio n The Raw Seasonal Ratio is used to calculate the Seasonal Index 109
Raw Seasonal Ratios n Now that we have an estimate for trend, we can solve our general model for seasonality – Season = Y / Trend n We use this formula to calculate the Raw Seasonal Ratio n The Raw Seasonal Ratio is used to calculate the Seasonal Index 109
 Seasonal Index n To calculate the Seasonal Index for each period, average the raw ratios for each similar period then center the averages about 1 n Divide each season’s average by the overall (grand) average to force the average of all Seasonal Indices to equal 1 110
Seasonal Index n To calculate the Seasonal Index for each period, average the raw ratios for each similar period then center the averages about 1 n Divide each season’s average by the overall (grand) average to force the average of all Seasonal Indices to equal 1 110
 Deseasonalized Data n Going back to the conceptual model, solve for trend: – Trend = Y / Season n This eliminates seasonal variation and isolates the trend n Now use the Least Squares method to compute the Trend 111
Deseasonalized Data n Going back to the conceptual model, solve for trend: – Trend = Y / Season n This eliminates seasonal variation and isolates the trend n Now use the Least Squares method to compute the Trend 111
 Forecast n Now that we have the Seasonal Indices and Trend, we can reseasonalize the data and generate the forecast – Y = Trend x Season 112
Forecast n Now that we have the Seasonal Indices and Trend, we can reseasonalize the data and generate the forecast – Y = Trend x Season 112
 Deciding Between Forecasting Models & Methods n Look at the errors over the backcast or for a holdout sample: Bias near zero – MAD, MAPE, & Std Error near Zero – Coefficient of Determination (R 2) near unity. – n How well does it perform in repeated uses and during validation with different data. 113
Deciding Between Forecasting Models & Methods n Look at the errors over the backcast or for a holdout sample: Bias near zero – MAD, MAPE, & Std Error near Zero – Coefficient of Determination (R 2) near unity. – n How well does it perform in repeated uses and during validation with different data. 113
 Deciding Between Forecasting Models & Methods n What if several models are approximately “equally good”? – The Rule of Parsimony (or using Occam’s Razor), we would choose the simplest, easiest, most cost effective model that meets our needs. 114
Deciding Between Forecasting Models & Methods n What if several models are approximately “equally good”? – The Rule of Parsimony (or using Occam’s Razor), we would choose the simplest, easiest, most cost effective model that meets our needs. 114


