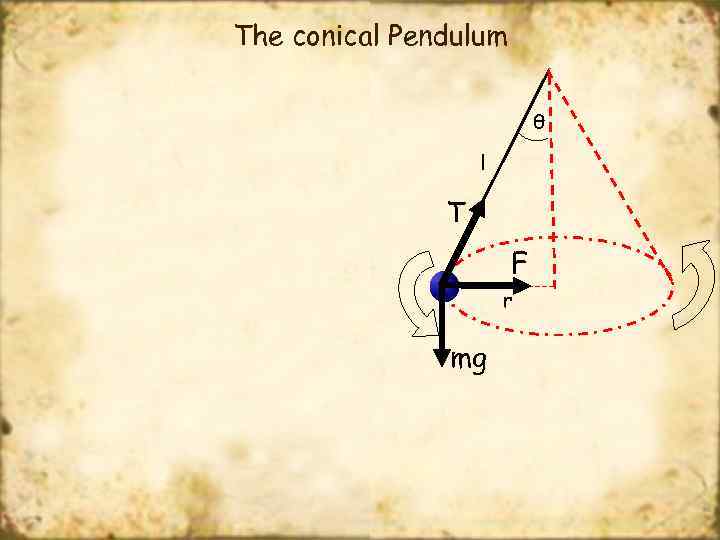
The conical Pendulum θ l T F r mg
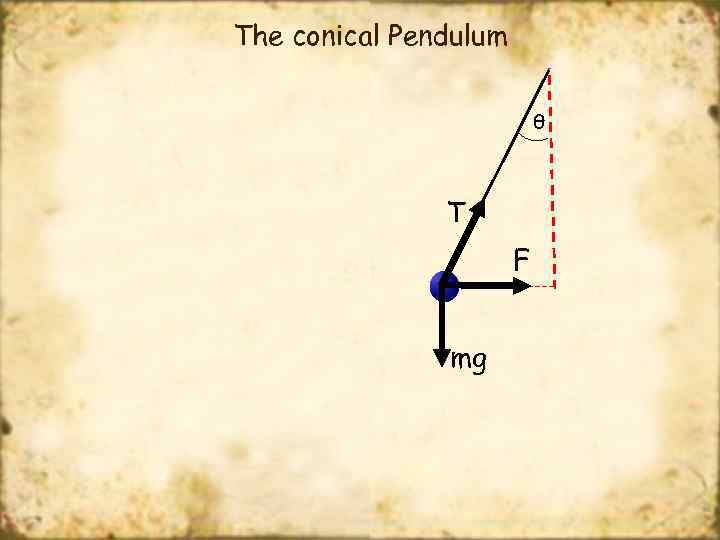
The conical Pendulum θ T F mg
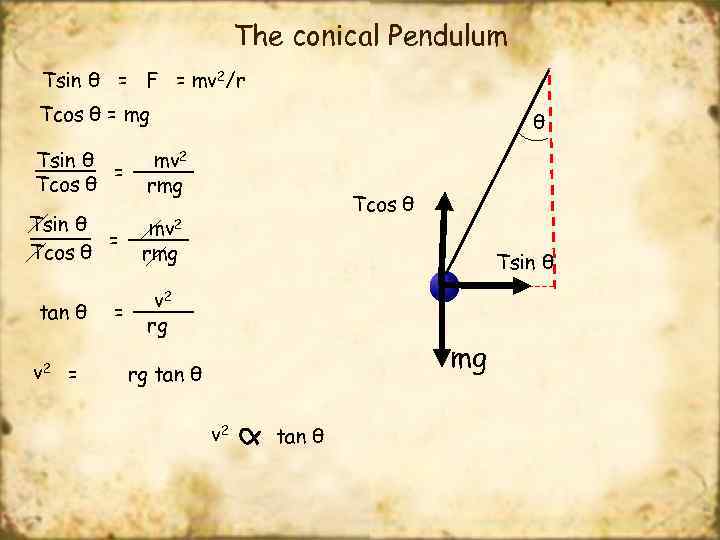
The conical Pendulum Tsin θ = F = mv 2/r Tcos θ = mg Tsin θ = Tcos θ mv 2 rmg Tsin θ = Tcos θ θ mv 2 rmg tan θ v 2 = = Tcos θ Tsin θ v 2 rg mg rg tan θ v 2 tan θ
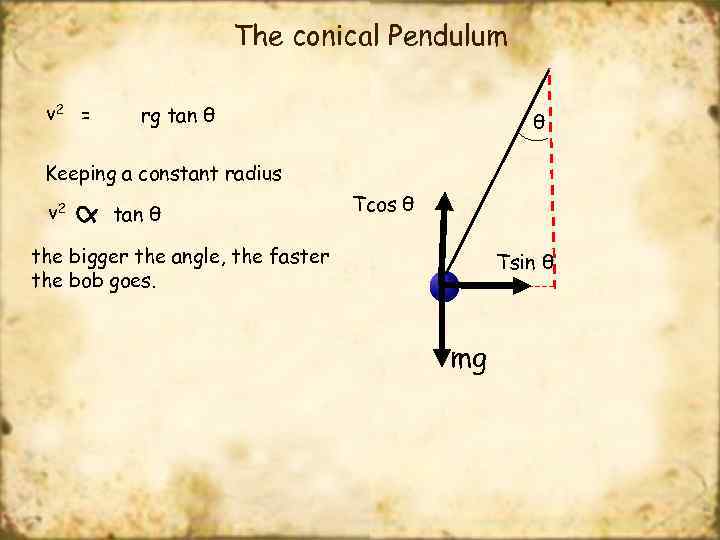
The conical Pendulum v 2 = rg tan θ θ Keeping a constant radius v 2 tan θ Tcos θ the bigger the angle, the faster the bob goes. Tsin θ mg
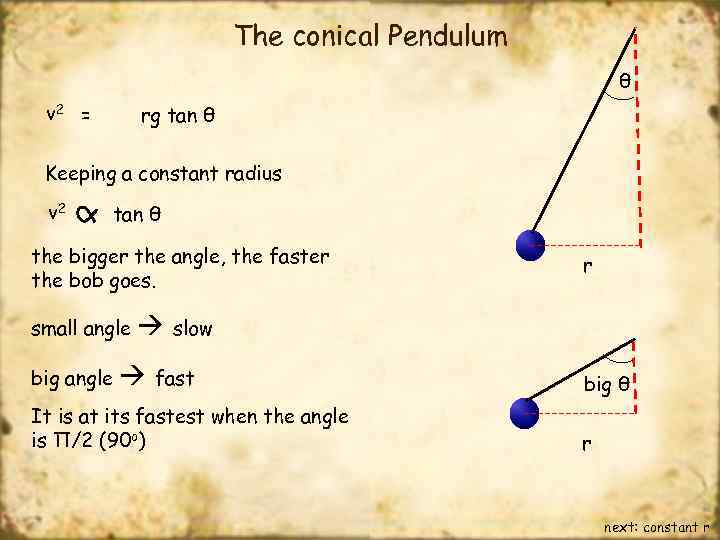
The conical Pendulum θ v 2 = rg tan θ Keeping a constant radius v 2 tan θ the bigger the angle, the faster the bob goes. small angle big angle r slow fast It is at its fastest when the angle is Π/2 (90 o) big θ r next: constant r
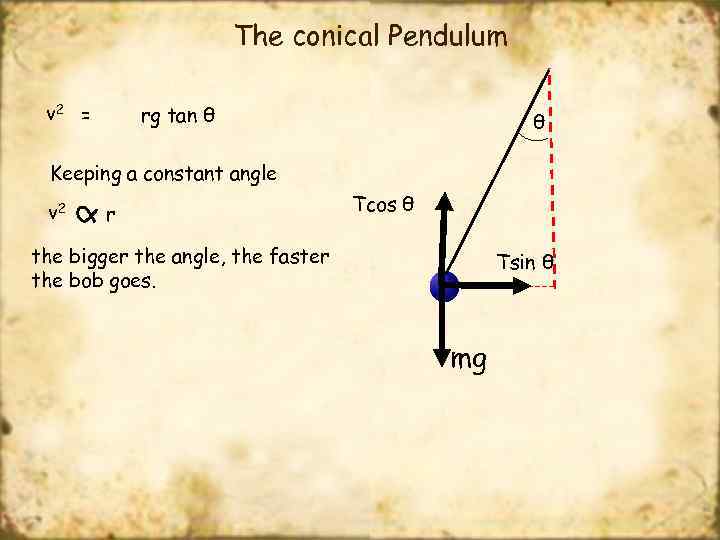
The conical Pendulum v 2 = rg tan θ θ Keeping a constant angle v 2 r Tcos θ the bigger the angle, the faster the bob goes. Tsin θ mg
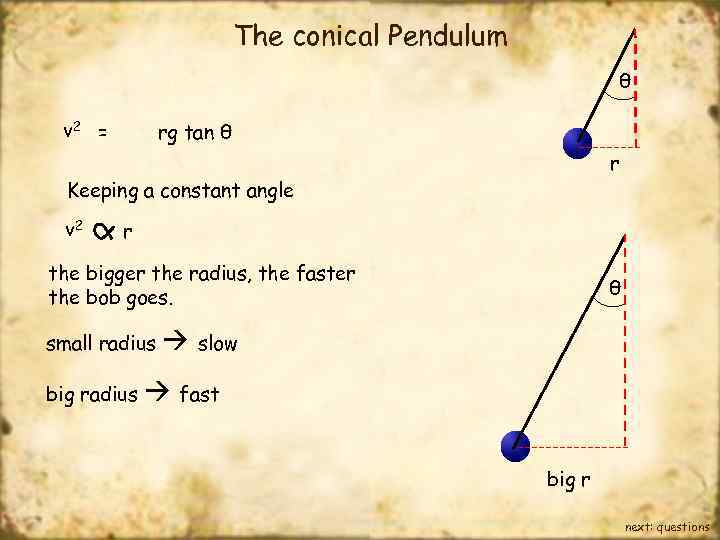
The conical Pendulum θ v 2 = rg tan θ r Keeping a constant angle v 2 r the bigger the radius, the faster the bob goes. small radius big radius θ slow fast big r next: questions
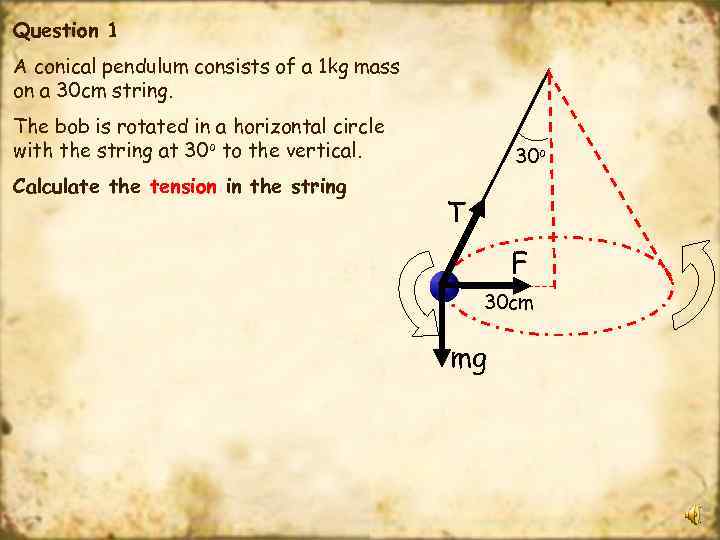
Question 1 A conical pendulum consists of a 1 kg mass on a 30 cm string. The bob is rotated in a horizontal circle with the string at 30 o to the vertical. Calculate the tension in the string 30 o T F 30 cm mg
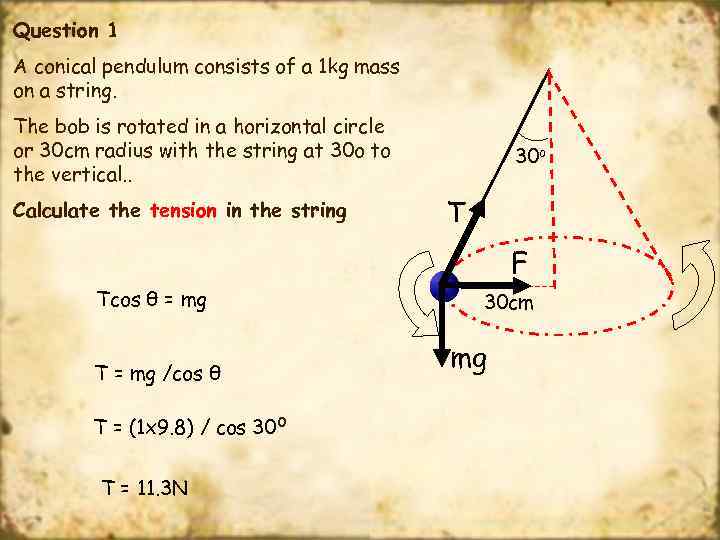
Question 1 A conical pendulum consists of a 1 kg mass on a string. The bob is rotated in a horizontal circle or 30 cm radius with the string at 30 o to the vertical. . Calculate the tension in the string 30 o T F Tcos θ = mg T = mg /cos θ T = (1 x 9. 8) / cos 30 o T = 11. 3 N 30 cm mg
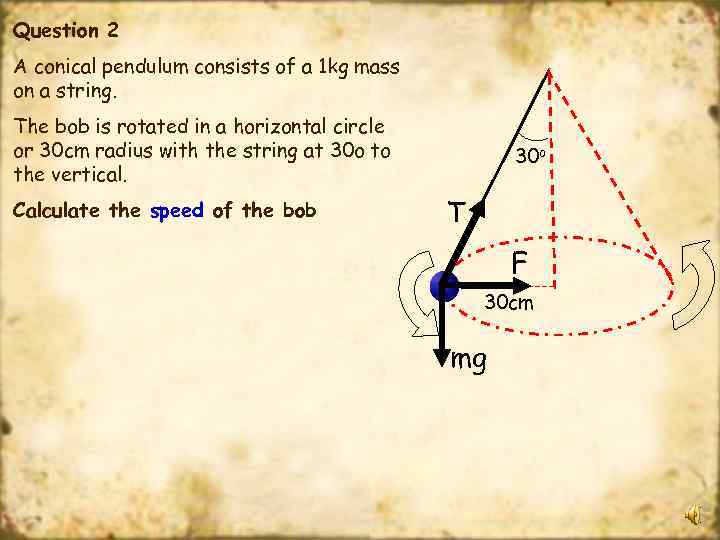
Question 2 A conical pendulum consists of a 1 kg mass on a string. The bob is rotated in a horizontal circle or 30 cm radius with the string at 30 o to the vertical. Calculate the speed of the bob 30 o T F 30 cm mg
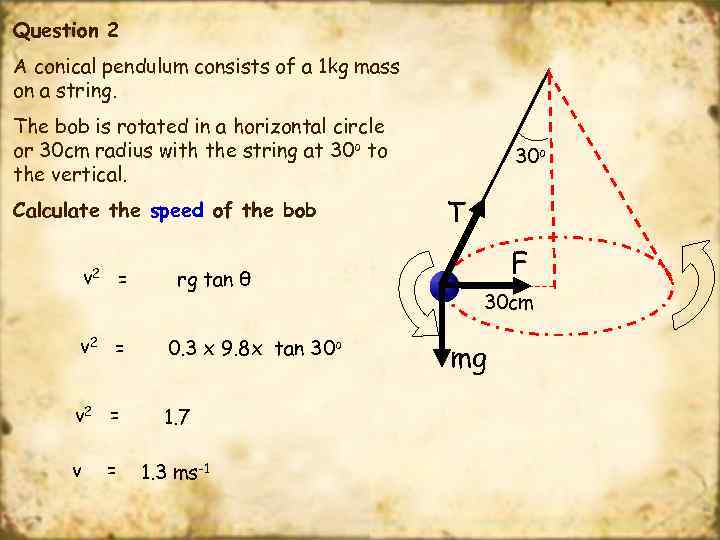
Question 2 A conical pendulum consists of a 1 kg mass on a string. The bob is rotated in a horizontal circle or 30 cm radius with the string at 30 o to the vertical. Calculate the speed of the bob v 2 = rg tan θ v 2 = 0. 3 x 9. 8 x tan 30 o v 2 = 1. 7 v = 1. 3 ms-1 30 o T F 30 cm mg
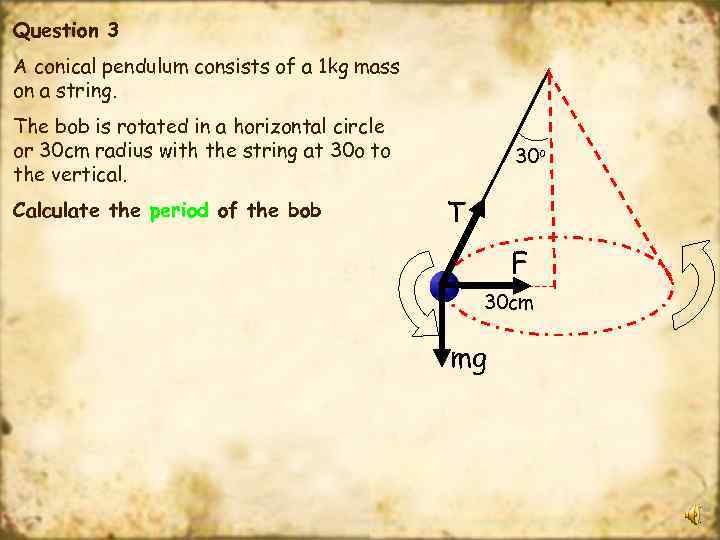
Question 3 A conical pendulum consists of a 1 kg mass on a string. The bob is rotated in a horizontal circle or 30 cm radius with the string at 30 o to the vertical. Calculate the period of the bob 30 o T F 30 cm mg
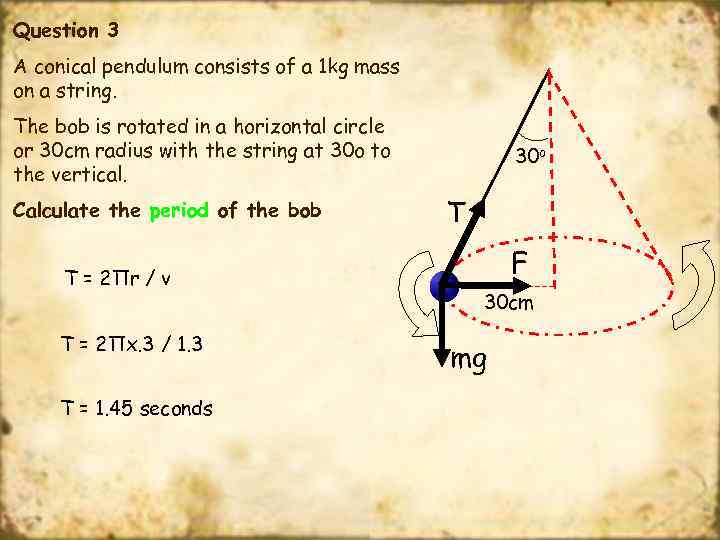
Question 3 A conical pendulum consists of a 1 kg mass on a string. The bob is rotated in a horizontal circle or 30 cm radius with the string at 30 o to the vertical. Calculate the period of the bob T = 2Πr / v T = 2Πx. 3 / 1. 3 T = 1. 45 seconds 30 o T F 30 cm mg

Question 4 A racetrack has a radius of 150 m and a banking angle of 25 o. What is the maximum velocity the car can go without skidding ? 25 o (ignore friction) R 25 o mg

Question 4 A racetrack has a radius of 150 m and a banking angle of 25 o. What is the maximum velocity the car can go without skidding ? 25 o (ignore friction) v 2 = v = R rg tan θ 150 x 9. 8 x tan 25 o 26. 2 ms-1 about 94 kmh-1 or 58 mph 25 o mg

Periodic Motion
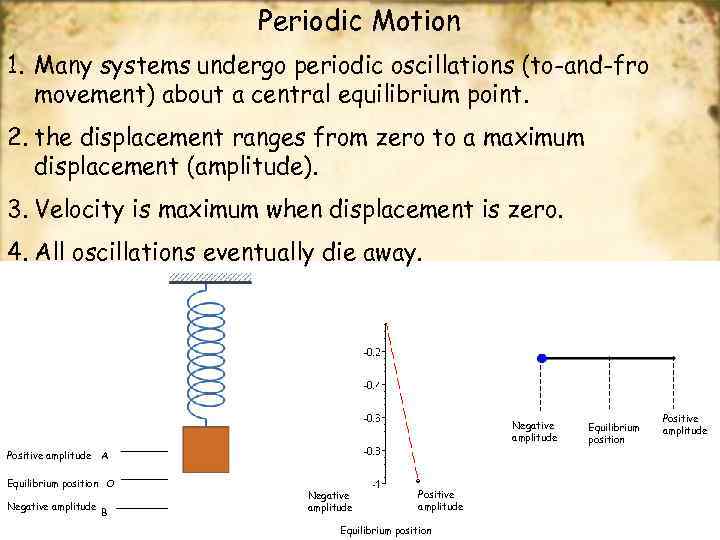
Periodic Motion 1. Many systems undergo periodic oscillations (to-and-fro movement) about a central equilibrium point. 2. the displacement ranges from zero to a maximum displacement (amplitude). 3. Velocity is maximum when displacement is zero. 4. All oscillations eventually die away. Negative amplitude Positive amplitude A Equilibrium position O Negative amplitude B Negative amplitude Positive amplitude Equilibrium position Positive amplitude
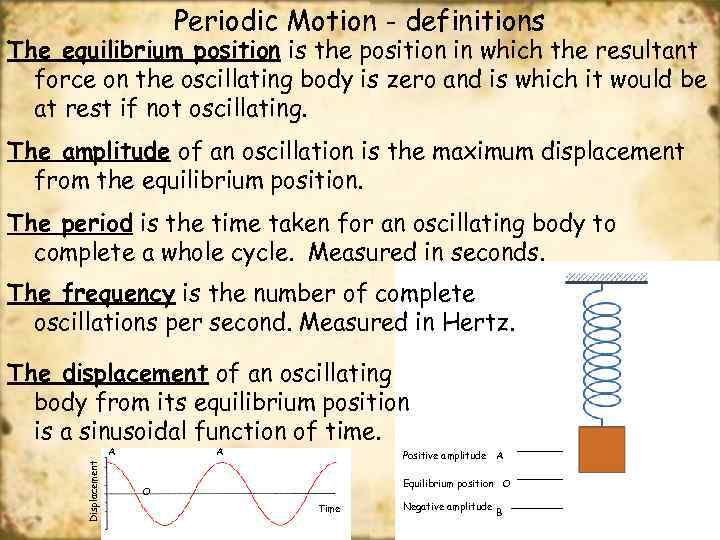
Periodic Motion - definitions The equilibrium position is the position in which the resultant force on the oscillating body is zero and is which it would be at rest if not oscillating. The amplitude of an oscillation is the maximum displacement from the equilibrium position. The period is the time taken for an oscillating body to complete a whole cycle. Measured in seconds. The frequency is the number of complete oscillations per second. Measured in Hertz. The displacement of an oscillating body from its equilibrium position is a sinusoidal function of time. Displacement A A Positive amplitude A Equilibrium position O O Time Negative amplitude B

Record the period or the frequency of the different oscillating systems provided.

A girl at the seaside whirls a bucket of water in a vertical circle of radius 0. 5 m. If the angular velocity is constant and she completes 3 revolutions in 2 seconds. Calculate the centripetal acceleration of the water in the bucket. ω = 2πf = 9. 4 rad s-1 a = ω2 r = 44. 4 ms-2
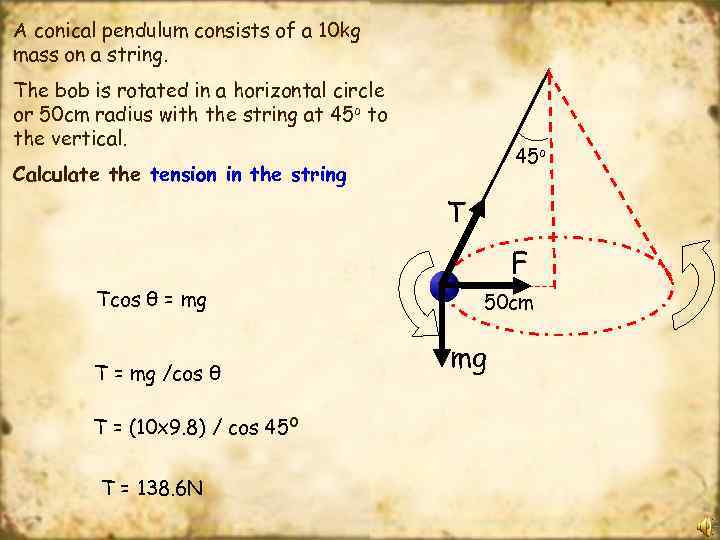
A conical pendulum consists of a 10 kg mass on a string. The bob is rotated in a horizontal circle or 50 cm radius with the string at 45 o to the vertical. 45 o Calculate the tension in the string T F Tcos θ = mg T = mg /cos θ T = (10 x 9. 8) / cos 45 o T = 138. 6 N 50 cm mg
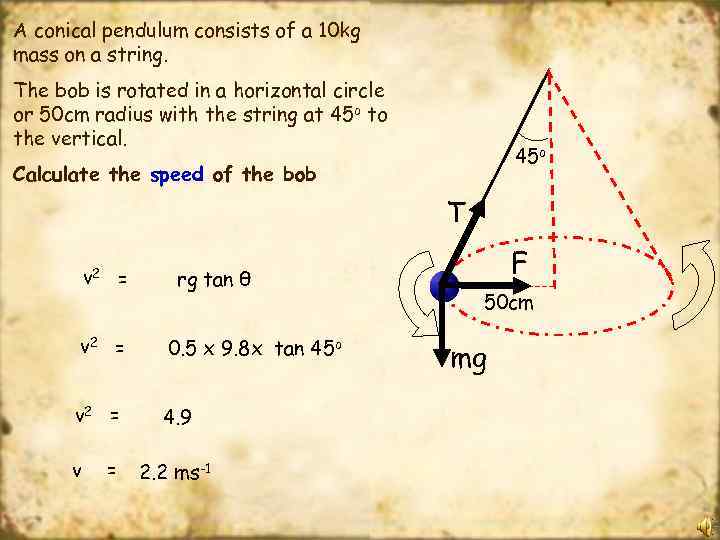
A conical pendulum consists of a 10 kg mass on a string. The bob is rotated in a horizontal circle or 50 cm radius with the string at 45 o to the vertical. 45 o Calculate the speed of the bob T v 2 = rg tan θ v 2 = 0. 5 x 9. 8 x tan 45 o v 2 = 4. 9 v = 2. 2 ms-1 F 50 cm mg
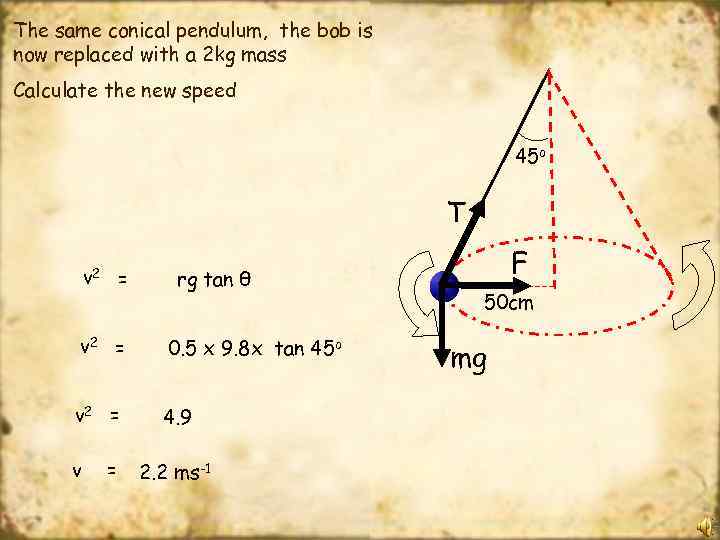
The same conical pendulum, the bob is now replaced with a 2 kg mass Calculate the new speed 45 o T v 2 = rg tan θ v 2 = 0. 5 x 9. 8 x tan 45 o v 2 = 4. 9 v = 2. 2 ms-1 F 50 cm mg
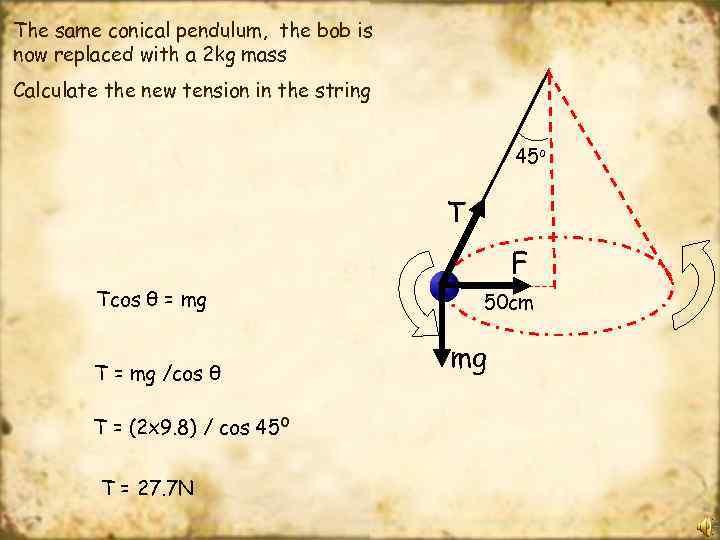
The same conical pendulum, the bob is now replaced with a 2 kg mass Calculate the new tension in the string 45 o T F Tcos θ = mg T = mg /cos θ T = (2 x 9. 8) / cos 45 o T = 27. 7 N 50 cm mg
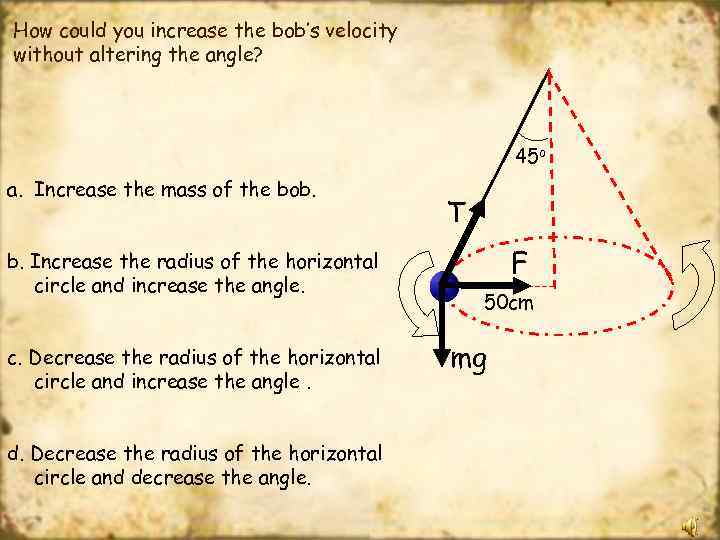
How could you increase the bob’s velocity without altering the angle? 45 o a. Increase the mass of the bob. b. Increase the radius of the horizontal circle and increase the angle. c. Decrease the radius of the horizontal circle and increase the angle. d. Decrease the radius of the horizontal circle and decrease the angle. T F 50 cm mg
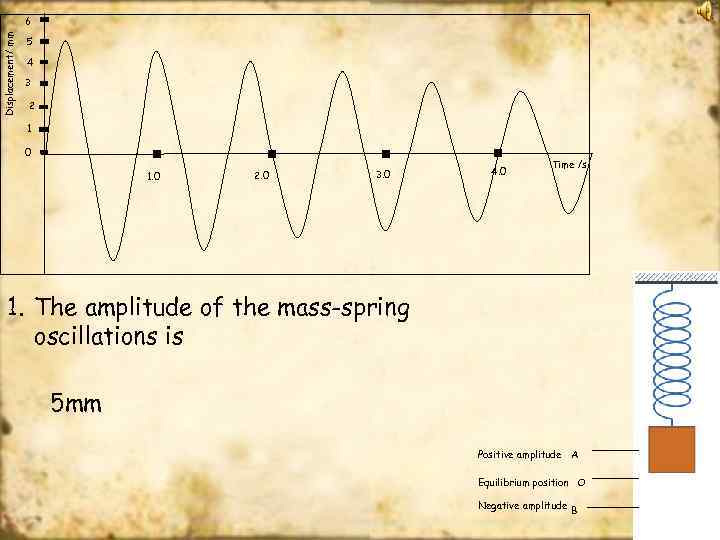
Displacement/ mm 6 5 4 3 2 1 0 1. 0 2. 0 3. 0 4. 0 Time /s 1. The amplitude of the mass-spring oscillations is 5 mm Positive amplitude A Equilibrium position O Negative amplitude B
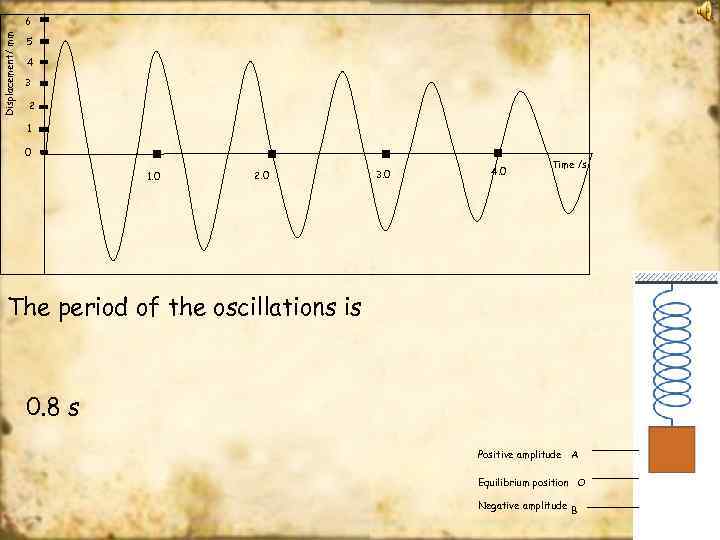
Displacement/ mm 6 5 4 3 2 1 0 1. 0 2. 0 3. 0 4. 0 Time /s The period of the oscillations is 0. 8 s Positive amplitude A Equilibrium position O Negative amplitude B
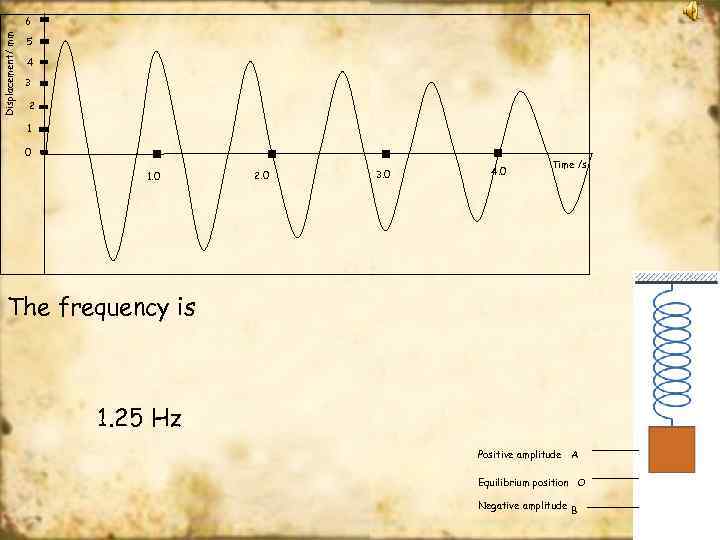
Displacement/ mm 6 5 4 3 2 1 0 1. 0 2. 0 3. 0 4. 0 Time /s The frequency is 1. 25 Hz Positive amplitude A Equilibrium position O Negative amplitude B
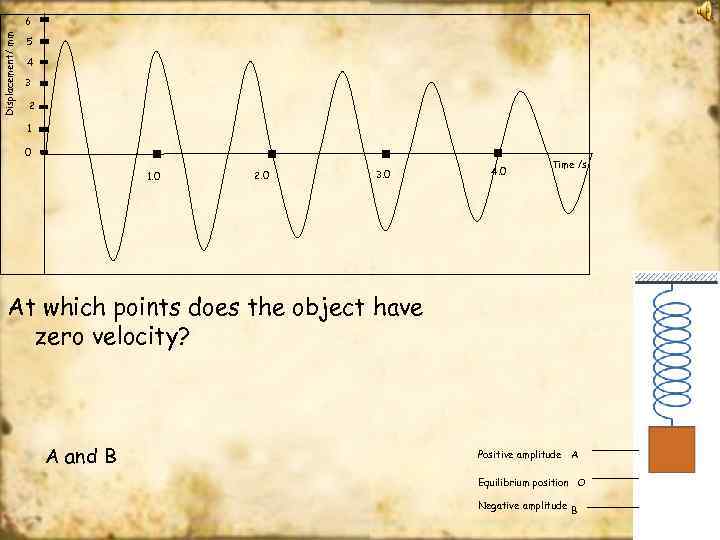
Displacement/ mm 6 5 4 3 2 1 0 1. 0 2. 0 3. 0 4. 0 Time /s At which points does the object have zero velocity? A and B Positive amplitude A Equilibrium position O Negative amplitude B

1. Carry out an investigation to see how the period of an oscillating spring is affected by the amount of mass attached to it. 2. Use a maximum of 600 g 3. represent your data in a graph. Is the period directly proportional to the mass? 4. There is a hypothesis that the square of the period should be directly proportional to the mass. Test this hypothesis. 5. Use your graph to work out the ‘unknown mass’.