ca3f90b2d6d894b14f844278ef5c06e4.ppt
- Количество слайдов: 25

The Bloom Paradox Ori Rottenstreich Joint work with Yossi Kanizo and Isaac Keslassy Technion, Israel
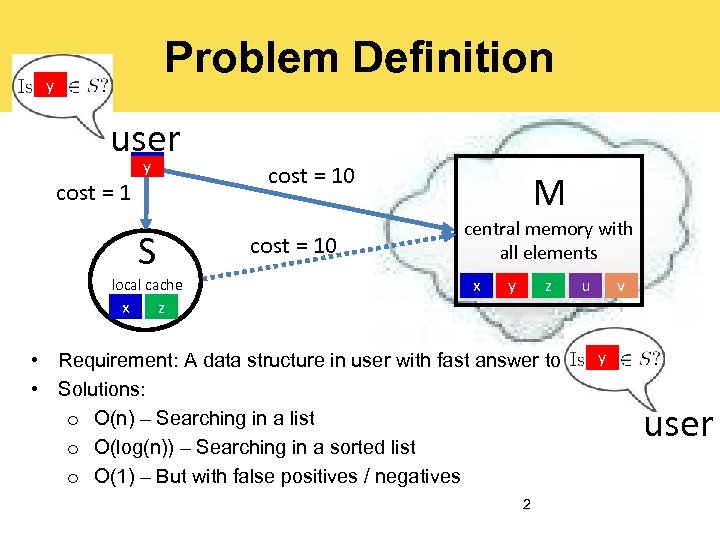
Problem Definition y x user x y cost = 1 S cost = 10 local cache x cost = 10 z M central memory with all elements x z y • Requirement: A data structure in user with fast answer to • Solutions: o O(n) – Searching in a list o O(log(n)) – Searching in a sorted list o O(1) – But with false positives / negatives 2 u v y user
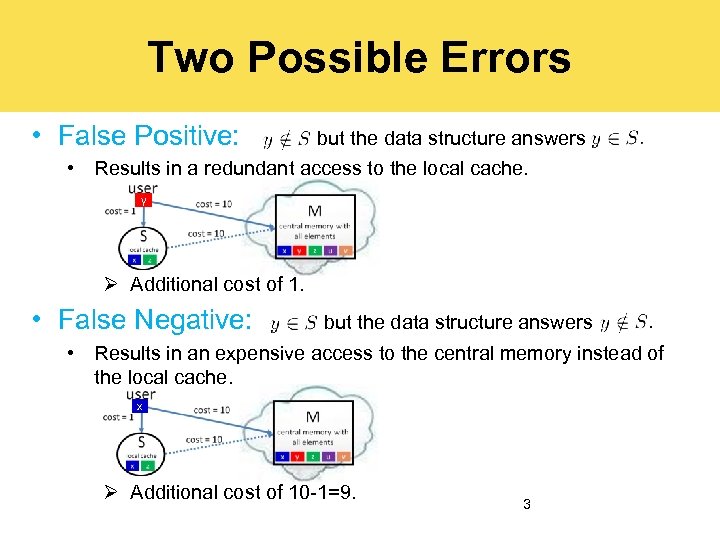
Two Possible Errors • False Positive: but the data structure answers • Results in a redundant access to the local cache. y Ø Additional cost of 1. • False Negative: but the data structure answers • Results in an expensive access to the central memory instead of the local cache. x Ø Additional cost of 10 -1=9. 3

Bloom Filters (Bloom, 1970) • Initialization: Array of 0 0 zero bits. 0 0 0 0 0 • Insertion: Each of the elements is hashed times, the corresponding bits are set. • Query: Hashing the element, checking that all bits are set. y x 1 0 1 0 0 1 x 1 1 1 0 1 11 0 1 z 0 1 1 0 0 1 1 1 w 1 0 0 • False positive rate (probability) of • No false negatives 4

Bloom Filters are Widely Used • • • Cache/Memory Framework Packet Classification Intrusion Detection Routing Accounting Beyond networking: Spell Checking, DNA Classification • Can be found in o Google's web browser Chrome o Google's database system Big. Table o Facebook's distributed storage system Cassandra o Mellanox's IB Switch System 5

Outline Ø Introduction to Bloom Filters Ø The Bloom Paradox Ø The Variable-Increment Counting Bloom Filter 6

The Bloom Paradox Sometimes, it is better to disregard the Bloom filter results, and in fact not to even query it, thus making the Bloom filter useless. 7
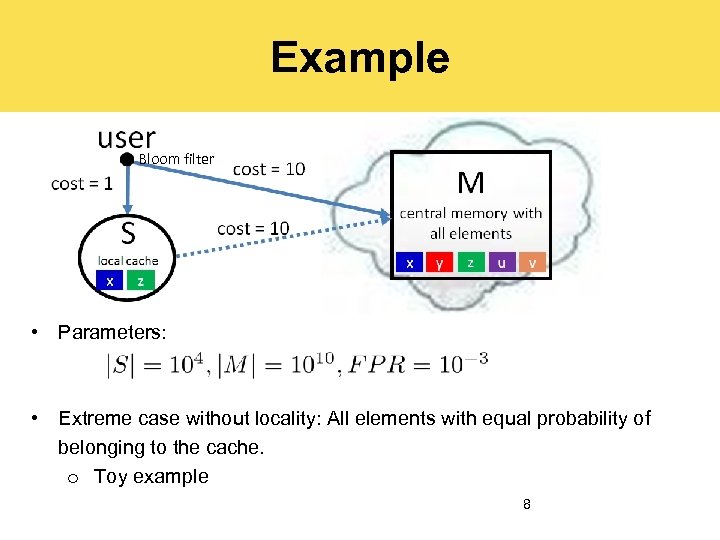
Example Bloom filter • Parameters: • Extreme case without locality: All elements with equal probability of belonging to the cache. o Toy example 8

The Bloom Paradox • Parameters: • Let be the set of elements that the Bloom filter indicates are in o In particular, no false negatives → • Intuition: B user Bloom filter cost = 1 S cost = 10 z . central memory with all elements x local cache x M . z y 9 u v

The Bloom Paradox • Parameters: • Let be the set of elements that the Bloom filter indicates are in o In particular, no false negatives → • Surprise: B Bloom filter cost = 1 S cost = 10 z . central memory with all elements x local cache x M . z y 9 u v

The Bloom Paradox • Parameters: • Let be the set of elements that the Bloom filter indicates are in o In particular, no false negatives → • Surprise: B Bloom filter . . The Bloom filter indicates the membership of elements. Only of them are indeed in .

The Bloom Paradox • When the Bloom filter states that , it is wrong with probability • Average cost if we listen to the Bloom filter: • Average cost if we don’t: = = The Bloom filter is useless!11 Don’t listen to the Bloom filter

Outline Ø Introduction to Bloom Filters Ø The Bloom Paradox Ø The Variable-Increment Counting Bloom Filter 12

Counting Bloom Filters (CBFs) • Bloom filters do not support deletions of elements. Simply resetting bits might cause false negatives. y x 1 0 1 1 0 0 0 • The solution: Counting Bloom filters - Storing array of instead of bits. o Insertion: Incrementing counters by one. o Deletion: Decrementing counters by one. o Query: Checking that counters are positive. y x +1 +1 0 +1 +1 1 0 0 2 0 +1 1 counters +1 0 1 • The same false positive probability. • Require too much memory, e. g. 57 bits per element for 0 .

Intuition for Variable Increments • Upon query, we should consider the exact values of the counters and not just their positiveness 0 1 0 2 y 5 0 1 8 3 0 2 1 z • Can we design a deterministic scheme that exploits the exact values of the counters? • Idea: Use variable increments to encode the element identity 14
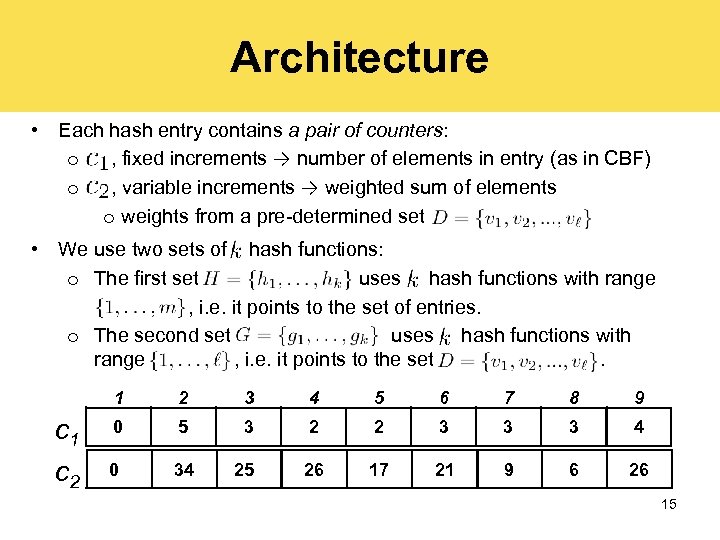
Architecture • Each hash entry contains a pair of counters: o , fixed increments → number of elements in entry (as in CBF) o , variable increments → weighted sum of elements o weights from a pre-determined set • We use two sets of hash functions: o The first set uses hash functions with range , i. e. it points to the set of entries. o The second set uses hash functions with range , i. e. it points to the set. 1 c 2 2 3 4 5 6 7 8 9 0 5 3 2 2 3 3 3 4 0 34 25 26 17 21 9 6 26 15

Insertion • Insertion: At each entry , the two counters are updated as follows. o from the set o • Example 1: 1 c 2 2 3 4 5 6 7 8 9 001 5 334 2 324 3 3 45 3 4 0 08 34 25 29 25 17 17 30 43 21 30934 13 26 +8 x +4 +13 z +4 16

Query • Query y ( with ) 1 c 2 2 3 4 5 6 7 8 9 0 5 3 2 3 3 4 0 34 25 17 30 21 30 13 26 4? 8? y? • We ask whether o 17 can be a sum of 2 elements from the set o 30 can be a sum of 3 elements from the set • No: • How should we pick the set of variable increments? We should use including 4 including 8 Sequences! 17

Bh Sequences • Definition 1: Let Then, with is a be a sequence of positive integers. sequence iff all the sums are distinct. • Example 2: All the sums of • elements of are distinct: Therefore, is a sequences are widely used in error-correcting codes. 18

The Bh-CBF Scheme Query • Example 3: is a sequence 1 c 2 2 3 4 5 6 7 8 9 0 5 3 2 3 3 4 34 25 17 30 21 30 13 26 0 1? 4? X? o Since , then the Bh-CBF can determine that 19
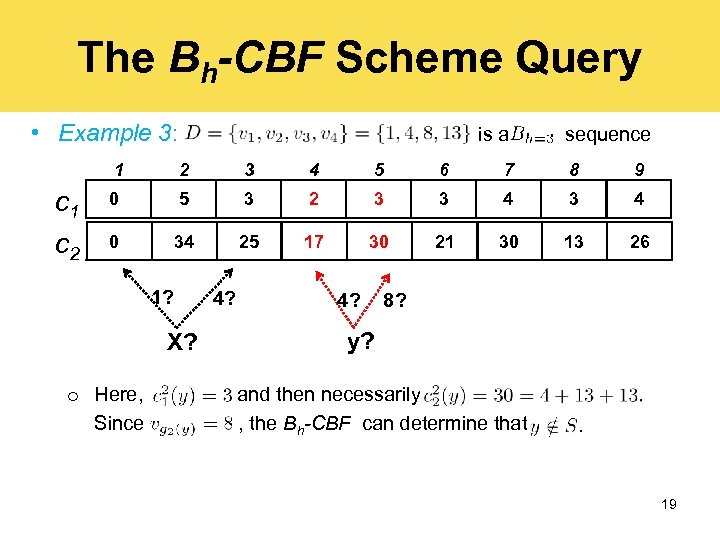
The Bh-CBF Scheme Operations The Bh-CBF Scheme Query • Example 3: is a sequence 1 c 2 2 3 4 5 6 7 8 9 0 5 3 2 3 3 4 0 34 25 17 30 21 30 13 26 1? X? o Here, Since 4? 8? y? and then necessarily , the Bh-CBF can determine that 19
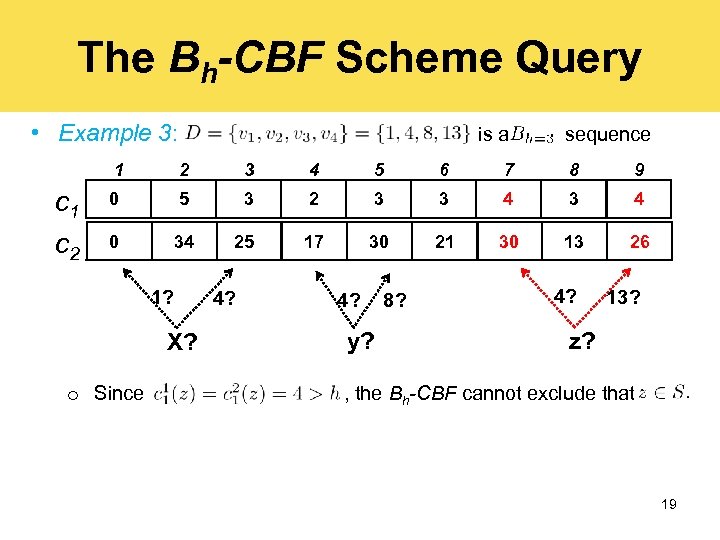
The Bh-CBF Scheme Operations The Bh-CBF Scheme Query • Example 3: is a sequence 1 c 2 2 3 4 5 6 7 8 9 0 5 3 2 3 3 4 0 34 25 17 30 21 30 13 26 1? X? o Since 4? y? 8? 4? 13? z? , the Bh-CBF cannot exclude that 19

Experimental Results • Internet trace (equinix-chicago) with real hash functions. For the Bh-CBF, (with ). 20

Concluding Remarks • The Bloom Paradox o Discovery of the Bloom paradox o Importance of the a priori membership probability • The Variable-Increment Counting Bloom Filter o Can extend many variants of the counting Bloom filter o First time sequences are presented in networking applications 21

Thank You
ca3f90b2d6d894b14f844278ef5c06e4.ppt