Hands-on 1_Blending of lines.pptx
- Количество слайдов: 11
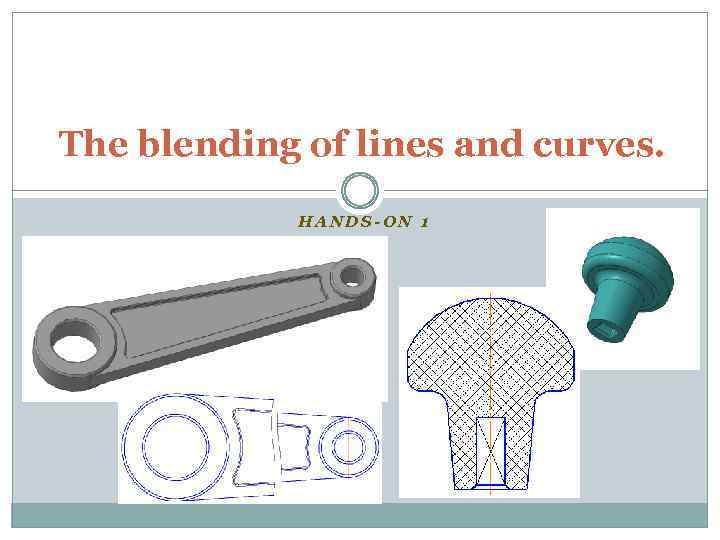
The blending of lines and curves. HANDS-ON 1

Principles of blending The blending of lines on technical drawing is used for: eliminating sharp edges and making them safer to handle; eliminating stress centre and making it stronger; avoiding extra machining and making it cheaper and etc.

Principles of blending To find the centre of an arc, radius R, which blends with two straight lines meeting at any angles m and n are given lines; R – radius of blending; Solution: 1) m' and n' are the lines of the blending centres of the lines m and n; 2) m' and n' are parallel to respective lines and equidistant to them of the R-distance; 3) m' and n' intersecting in point O; O is a centre of blending; 4) Points A and B are the points of blending, They are determined as a intersection of the perpendicular passed through O to the given lines m and n.

Principles of blending To find the centre of an arc, radius R, which external blends with the line and circle m is a given line; R 1 – radius of a given circle; R – radius of blending; Solution: 1) m' is the line of the blending centres of the line m; 2) m' is parallel to m line and equidistant to it of the R-distance; 3) To draw the arc with radius R+R 1 and centre in point O 1; 4) O is a centre of blending – intersection of the arc (R+R 1) and m'; 5) Points A and B are the points of blending: A – result of intersection of perpendicular through O to m-line; B – intersection of the given circle and line of O and O 1 connection.

Principles of blending To find the centre of an arc, radius R, which internal blends with the line and circle m is a given line; R 1 – radius of a given circle; R – radius of blending; Solution: 1) m' is the line of the blending centres of the line m; 2) m' is parallel to m line and equidistant to it of the R-distance; 3) To draw the arc with radius R-R 1 and centre in point O 1; 4) O is a centre of blending – intersection of the arc (R-R 1) and m'; 5) Points A 2 and B 1 are the points of blending: A 2 – result of intersection of perpendicular through O to m-line; B 1 – intersection of the given circle and line of O and O 1 connection.

Principles of blending To find the centre of an arc, radius R, which external blends with two circles m and n are given circles; R 1 and R 2 – radiuses of a given circles; R – radius of blending; Solution: 1) To draw two arcs: m' with radius R+R 1 and centre in point O 1 and n' - with radius R+R 2 and centre in point O 2; 2) O is a centre of blending – intersection of the arc m' (R+R 1) with arc n' (R+R 2); 3) Points A and B are the points of blending: A – result of intersection of line OO 1 with given circle m; B – result of intersection of line OO 2 with given circle n.
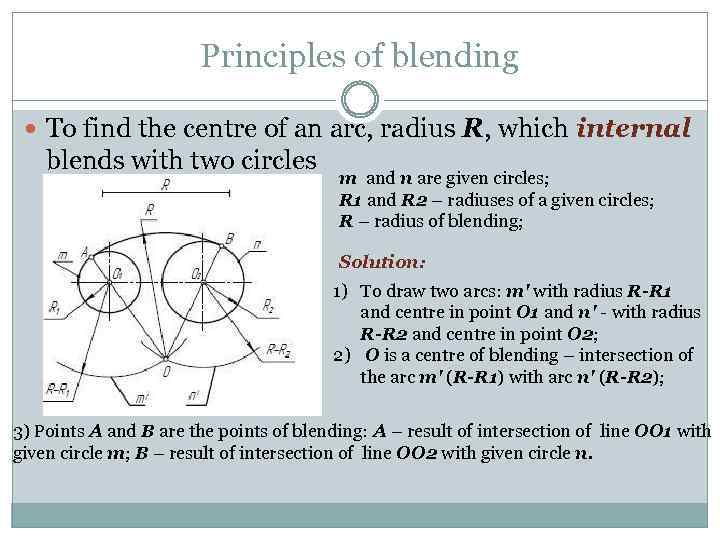
Principles of blending To find the centre of an arc, radius R, which internal blends with two circles m and n are given circles; R 1 and R 2 – radiuses of a given circles; R – radius of blending; Solution: 1) To draw two arcs: m' with radius R-R 1 and centre in point O 1 and n' - with radius R-R 2 and centre in point O 2; 2) O is a centre of blending – intersection of the arc m' (R-R 1) with arc n' (R-R 2); 3) Points A and B are the points of blending: A – result of intersection of line OO 1 with given circle m; B – result of intersection of line OO 2 with given circle n.
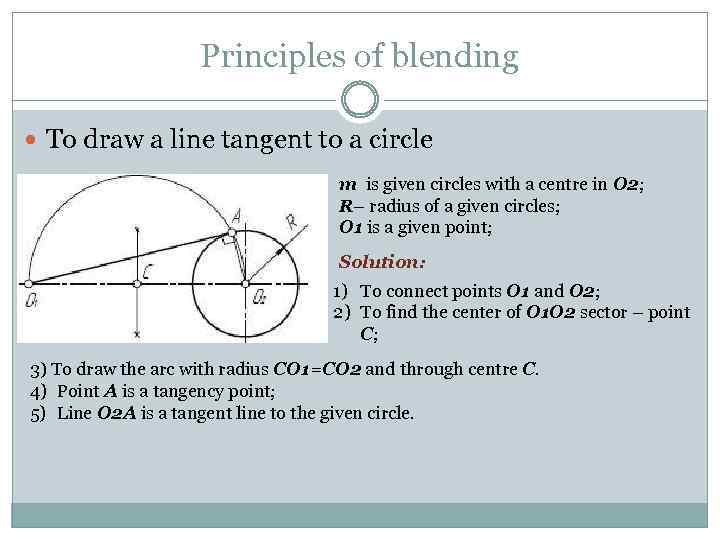
Principles of blending To draw a line tangent to a circle m is given circles with a centre in O 2; R– radius of a given circles; O 1 is a given point; Solution: 1) To connect points O 1 and O 2; 2) To find the center of O 1 O 2 sector – point C; 3) To draw the arc with radius CO 1=CO 2 and through centre C. 4) Point A is a tangency point; 5) Line O 2 A is a tangent line to the given circle.

Principles of blending To draw a line tangent to two circles m is given circles with a centre in O 1 and R 1– radius of a given circles; n is given circles with a centre in O 2 and R 2– radius of a given circles; Solution: 1) To connect points O 1 and O 2; 2) To find the center of O 1 O 2 sector – point C; 3) To draw auxiliary circle through the center of a larger circle O 2 with radius R 2 -R 1; 4) To draw the arc with radius CO 1=CO 2 and through centre C. 5) Point K is a point of two auxiliary circles intersection and it is a point of radius O 2 B passing which is get to the tangency point B; 6) Tangency point A may be found by the line O 1 A which is parallel to O 2 B. 7) Line AB is a tangent line to the given circles.
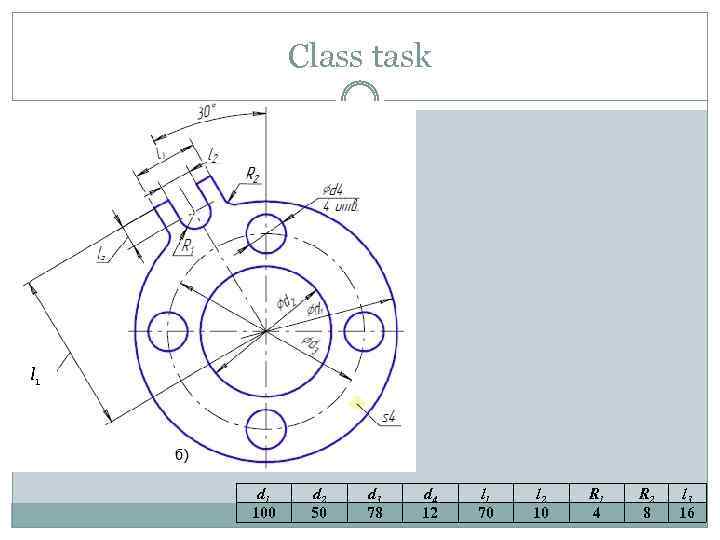
Class task l 1 d 1 100 d 2 50 d 3 78 d 4 12 l 1 70 l 2 10 R 1 4 R 2 8 l 3 16
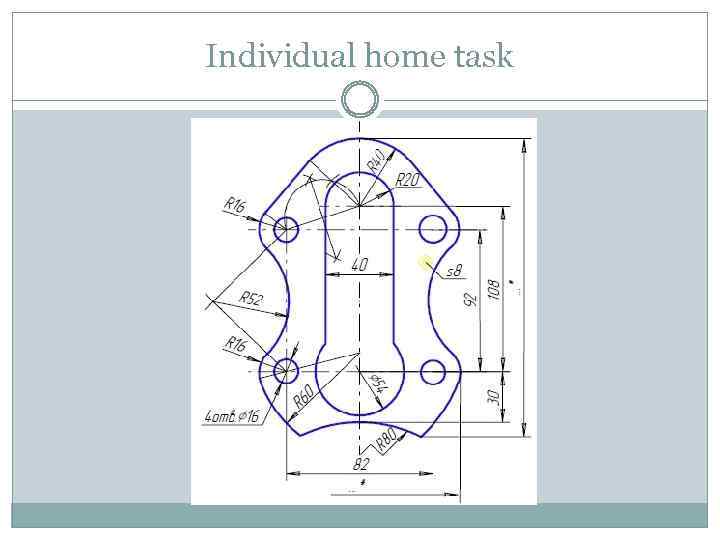
Individual home task
Hands-on 1_Blending of lines.pptx