4771c93660e095f44cb9d1fb2e845b6f.ppt
- Количество слайдов: 34

The Beginning of Microeconomics Different Paths

Several Paths u Mathematical • Partial Equilibrium – Alfred Marshall • General Equilibrium – Leon Walras • Distribution – Wilfredo Pareto

Several Paths (cont. ) u Non-Mathematical • Laissez-faire – Austrian Economics • Institutional – Thorstein Veblen

Mathematical

Antoine-Augustin Cournot 1801 -1877

Antoine-Augustin Cournot (cont. ) u Ecole Normal de Paris (studied mathematics) u Work as assistant to Marshall Gouvin Saint. Cyr (Napoleon’s general) u Doctorate from the University of Paris u His work attracted the attention of Poisson who help him find a teaching job at Lyons in 1834

Antoine-Augustin Cournot (cont. ) u He was also Inspector General Education (succeeding Ampere) u In addition he was superintendent to Grenoble and Dijon Academy u Became blind and finally retired in 1862

Antoine-Augustin Cournot (cont. ) u Major Works: • Exposition of the Theory of Chance and Probability • Research Into the Mathematical Principles of the Theory of Wealth u Other later works do no include mathematics

Antoine-Augustin Cournot (cont. ) u There authors, like Smith and Say, who, in writing on Political Economy, have preserved all the beauties of purely literary style; but there are others, like Ricardo, when treating the most abstract questions, or when seeking great accuracy, have not bee able to avoid algebra, an have only disguised it under arithmetical calculations of tiresome length. Any one who understands algebraic notation, reads at a glance in an equation results reached arithmetically only with great labor and pains (Mathematical Principles, p. 4)

Antoine-Augustin Cournot (cont. ) First to place Law of Demand Mathematical terms D = f(P) where d. D/d. P < 0 First to show the rule to maximize profits = P*D - (D) d /d. P = d. D/d. P*P + D - d /D*d. P/P = 0 d. D/d. P*P + D = d /D*d. P/P MR = MC

Antotine-Augustin Cournot (cont. ) Graphically Price, Costs MC AR = Demand Quantity MR Costs, Revenues, Profits TR TC Quantity

Antoine-Augustin Cournot (cont. ) u Duopoly Analysis • IMPORTANCE: – Interdependence of firm’s output – Uncertainty • LEAD TO – Monopolistic Competition – Game Theory

Antoine-Augustin Cournot (cont. ) u ASSUMPTIONS • • • Two sellers Know the total demand Ignore the output each is to produce Costless production Zero Output Conjectural variation – i. e. a conjecture that firm B will have no output reaction to firm’s A actions
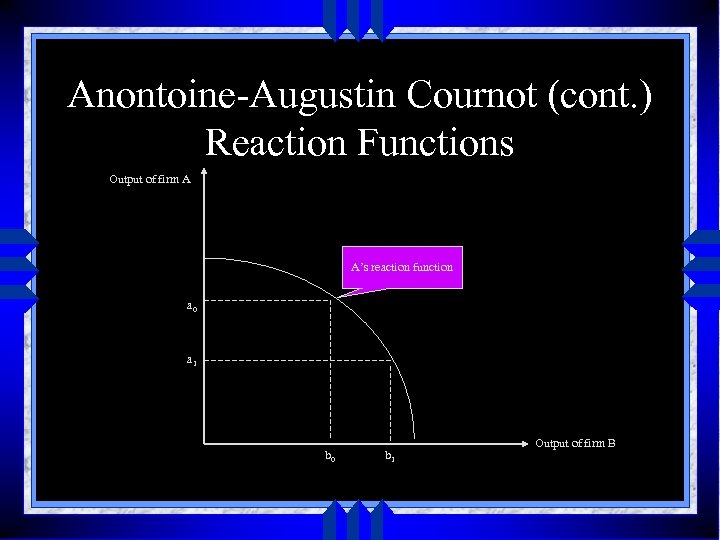
Anontoine-Augustin Cournot (cont. ) Reaction Functions Output of firm A A’s reaction function a 0 a 1 b 0 b 1 Output of firm B
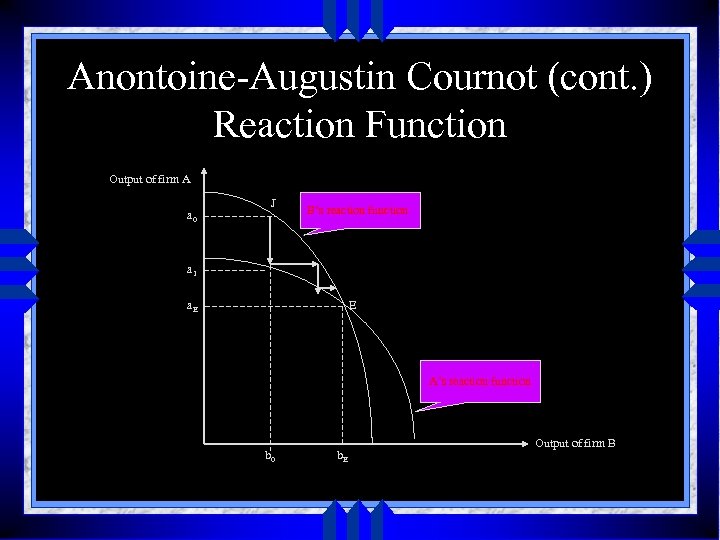
Anontoine-Augustin Cournot (cont. ) Reaction Function Output of firm A a 0 J B’s reaction function a 1 a. E E A’s reaction function b 0 b. E Output of firm B

Léon WALRAS (1834 -1910) General Equilibrium

Biography u His father, Auguste Walras, was a classmate of Cournot. u While not to the extent of young Mill, Auguste was the teacher of Léon. u Not a brilliant student, in fact he flunked the math portion of the admission exam to the École Polytechnique

General Equilibrium u Basic Premise: • Demand Supply are functions of several variables all of which are constantly being adjusted directly or indirectly u Consequently: • Rather than looking for individual impact of the specific variable we look for general equilibrium as direct adjustments of the variables occur

General Equilibrium u Equations: • T, T’’ different kinds of land (classical rent notion) • P, P’’ different kinds of labor (unlike modern marginal product notion) • K, K’’ different kinds of capital

General Equilibrium u Additional • • • Notation: m final goods: a, b, c, …. marginal utility function for individual r = q Price of final goods pb, pc, pd, …. Price of factor of Production pt, pp, pk, …. Household starts with given factors of production qt, qp, qk, ….

General Equilibrium u Additional Notation (cont. . ): • Quantity of factors of production offered by household: ot, op, ok, …. where on > 0 if household is offering factor and on < 0 if household is demanding factor (for n = t, p, k, …) • Finally, household demand for final goods is db, dc, dd, ….

General Equilibrium u Since there is no money the system uses a numeraire. For simplicity allow numeraire to be a. Thus, Pa = 1. u Allowing for equilibrium in the household sector Þ • otpt + oppp+ okpk + …. = da + dbpb+ dcpc + …. u since there are m commodities and n factors there are m+n unknowns

General Equilibrium u To maximize utility: • a) Marginal utility of factors held must be proportional to their price • t(qt - ot) = pt a(da) • p(qp - op) = pp a(da) • k(qk - ok) = pk a(da) • where there are n of these equations.

General Equilibrium u To maximize utility: • b) Marginal utility of commodities consumed must be proportional to their price • b(dt) = pb a(da) • c(dp) = pc a(da) • d(dk) = pd a(da) • where there are m-1 of these equations.

General Equilibrium u Demand functions are (m-1): • db = fb(pt, pp, pk, …, pb, pc, pd, …) • dc = fc(pt, pp, pk, …, pb, pc, pd, …) u Supply functions are (n): • ot = ft(pt, pp, pk, …, pb, pc, pd, …) • op = fp(pt, pp, pk, …, pb, pc, pd, …)

General Equilibrium u Recall that this was at the individual level. At the “macro” level then with the assumption of summation we would get: • Dn = S dn where n = a, b, c, …. and • On = S on where n = t, p, k, …. u This gives us a total of 2 m+2 n-1 unknowns.

Vilfredo Pareto July 15, 1848 -August 19, 1923 u Son of a Genoese father and a French mother was trained as an engineer u He left business at the age of 45 and accepted the chair of Lausanne vacated by the retirement of Walras u Bad health and a sizable inheritance allowed him an earlier retirement

Vilfredo Pareto u He went to live to Celigny on the Lake of Geneva u He grew to be known as the “lone thinker of Celigny” u Lived in a house with many cats named “Villa Angora” u Know as both a sociologist and an economist

Vilfredo Pareto u Pareto married in 1889. His new spouse Dina Bakunin, a Russian, apparently loved an active social life, which was rather in conflict with Pareto's own love of privacy and solitude. After twelve years of marriage Dina abandoned her husband. His second wife, Jane Regis, joined him shortly after the collapse of his marriage and the two remained devoted to one another throughout the remainder of Pareto's life.

Vilfredo Pareto u He spend some time helping out political exiles from Italy u He was very much against Marxian economics u He strongly believed people well selfserving as Adam Smith had portrayed

Vilfredo Pareto u Furthermore, in his work in sociology he strongly advocated the rule of the elite u Because of this, some considered him to be a fascist u This believe isolated him even further

Vilfredo Pareto u First person to conceive of the distribution of income in terms of a statistical distribution u He argued that if 100 persons were left in an island with equal amount of income u A year later, thru deceit, treachery, and other methods only a small portion of the population would have largest amount of income
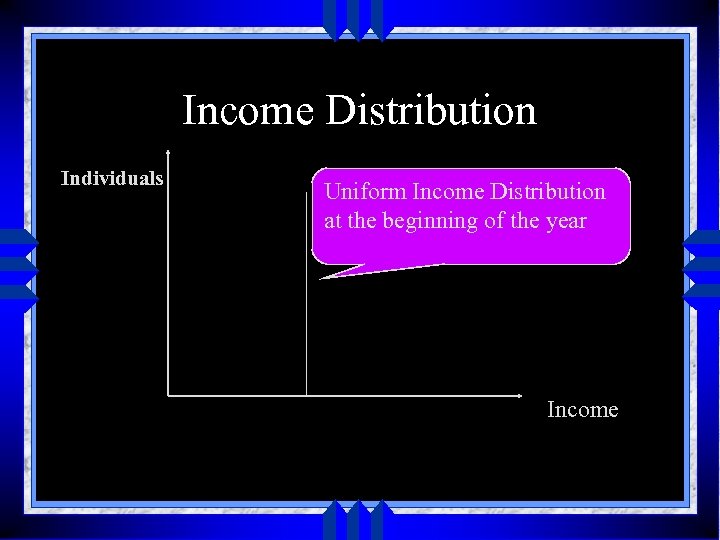
Income Distribution Individuals Uniform Income Distribution at the beginning of the year Income
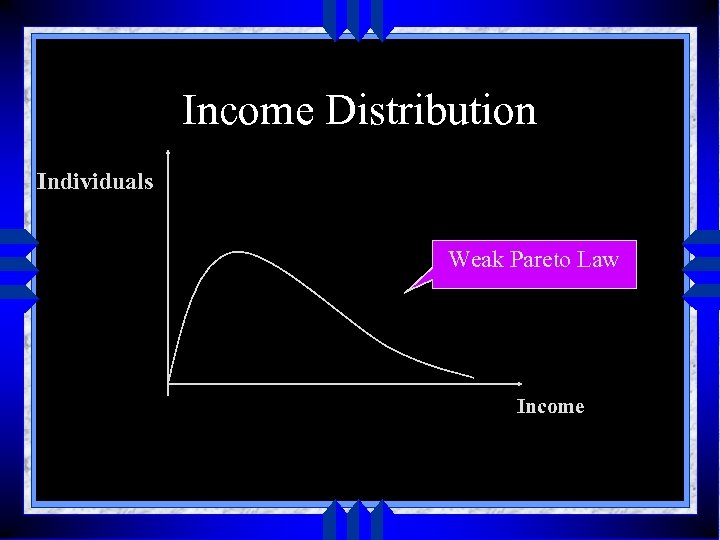
Income Distribution Individuals Weak Pareto Law Income
4771c93660e095f44cb9d1fb2e845b6f.ppt