The Approach of Modern AI Stuart Russell Computer

The Approach of Modern AI Stuart Russell Computer Science Division UC Berkeley

Outline The History of AI: A Rational Reconstruction Unifying Formalisms Future Developments Structure in behaviour Cumulative learning Agent architectures Tasks and platforms Open problems

Early history

Early history contd. • No integrated intelligent systems discipline emerged from the 1950 s • Different groups had different canonical problems and incompatible formalisms – Control theory: real vectors, linear/Gaussians – OR: atomic states, transition matrices – AI: first-order logic – Statistics: linear regression, Gaussian mixtures

Diaspora

Reunification(s)

Formalisms • Communication among human mathematicians vs. abstract model of actual computational processes => focus on concrete syntax, semantics, completeness • Multiple special-purpose models and algorithms vs. general representation and inference Þ can learn new things (e. g. , multiplayer games) without qualitatively new representations and algorithms Þ need efficient special-case behavior to “fall out” from general methods applied to particular problems

[Milch, 2006]

[Milch, 2006]

Expressiveness • Expressive language => concise models => fast learning, sometimes fast inference – E. g. , rules of chess: 1 page in first-order logic, 100, 000 pages in propositional logic, 1038 pages as atomic-state model • Significant progress occurring, expanding contact layer between AI systems and real -world data

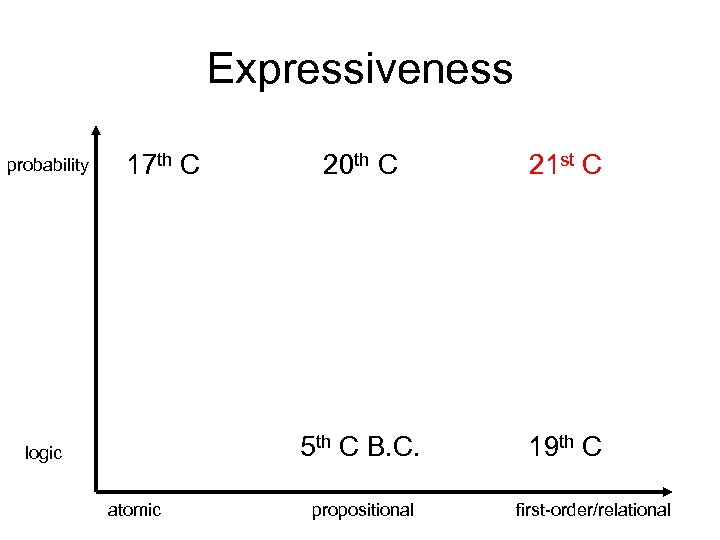Expressiveness probability 17 th C atomic 21 st C 5 th C B. C. logic 20 th C 19 th C propositional first-order/relational

Digression: GOFAI vs. Modern AI • Technically, each logic is a special case of the corresponding probabilistic language • Does probabilistic inference operate in the deterministic limit like logical inference? – One hopes so! – MCMC asymptotically identical to greedy SAT algorithms – Several algorithms exhibit “default logic” phenomenology • Modern AI should build on, not discard, GOFAI

First-order probabilistic languages • Gaifman [1964]: – distributions over first-order possible worlds • Halpern [1990]: – syntax for constraints on such distributions • Poole [1993] and several others: – KB defines distribution exactly – assumes unique names and domain closure • Milch et al [2005] and others: – distributions over full first-order possible worlds • generative models for events and existence – complete inference for all well-defined models

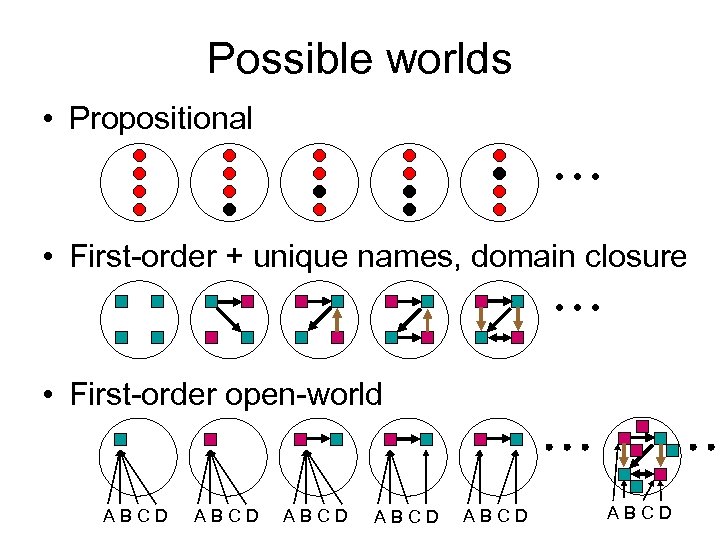Possible worlds • Propositional • First-order + unique names, domain closure • First-order open-world ABCD ABCD

Why does this matter? • What objects are referred to in the following sentence?

Why does this matter? • What objects appear in this image?

Unifications • Bayes nets [Pearl, 1988] led to the integration of (parts of) machine learning, statistics, KR, expert systems, speech recognition • First-order probabilistic languages may help to unify the rest of ML and KR, information extraction, NLP, vision, tracking and data association

Structure in behaviour • One billion seconds, one trillion (parallel) actions • Unlikely to be generated from a flat solution to the unknown POMDP of life • Hierarchical structuring of behaviour: enunciating this syllable saying this word saying this sentence explaining structure in behaviour giving a talk about AI …….

Hierarchical reinforcement learning • Hierarchical structure expressed as partial program – declarative procedural knowledge: what (not) to do • Key point: decisions within “subroutines” are independent of almost all state variables – E. g. , say(word, prosody) not say(word, prosody, NYSEprices, NASDAQ…) • Value functions decompose into additive factors, both temporally and functionally => fast learning • Decisions depend on internal + external state! – E. g. , I don’t even consider selling IBM stock during talk

HRL contd. • Complete learning algorithms exist for general-purpose, concurrent partial programming languages, but. . . • We need a KR subfield for “know-how” • Where do subroutines come from? • More generally, how are useful composites (objects, actions) built up?

Learning data knowledge

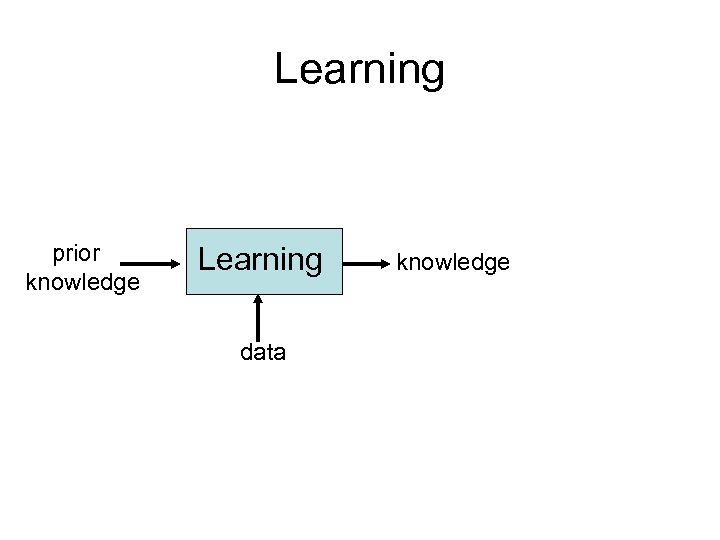Learning prior knowledge Learning data knowledge

Learning prior knowledge Learning data knowledge

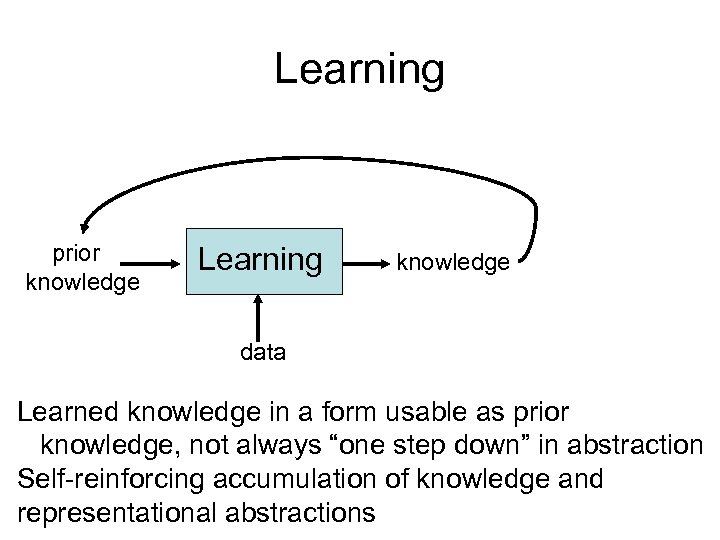Learning prior knowledge Learning knowledge data Learned knowledge in a form usable as prior knowledge, not always “one step down” in abstraction Self-reinforcing accumulation of knowledge and representational abstractions

Agent architectures • Core: state estimation maintains belief state – Lots of progress; extend to open worlds • • Reflex: π(s) Action-value: argmaxa Q(s, a) Goal-based: a such that G(result(a, s)) Utility-based: argmaxa E(U(result(a, s))) Would be nice to understand when one is better (e. g. , more learnable) than another Need an agent-building language providing composition and decomposition of architectural components

Metareasoning Computations are actions too Controlling them is essential, esp. for model-based architectures that can do lookahead and for approximate inference on intractable models Effective control based on expected value of computation Methods for learning this must be built-in – brains unlikely to have fixed, highly engineered algorithms that will correctly dictate trillions of computational actions over agent’s lifetime

A science of architecture • My boxes and arrows vs your boxes and arrows? • Well-designed/evolved architecture solves what optimization problem? What forces drive design choices? – Generate optimal actions – Generate them quickly – Learn to do this from few experiences • Each by itself leads to less interesting solutions – omitting learnability favours the all-compiled solution – omitting resource bounds favours Bayes-on-Turing-machines • Bounded-optimal solutions have interesting architectures and can be found for some nontrivial cases

Challenge problems should involve… Continued existence Behavioral structure at several time scales (not just repetition of small task) Finding good decisions should sometimes require extended deliberation Environment with many, varied objects, nontrivial perception (other agents, language optional) Examples: cook, house cleaner, secretary, courier Wanted: a human-scale dextrous 4 -legged robot + simulation-based CAD for vision-based robotics

Open problems • Learning better representations – need a new understanding of reification/generalization – Why did Eurisko’s nested loops run out of gas? • Learning new behavioural structures • Generating new goals from utility soup • Do neuroscience and cognitive science have anything to tell us? • What if we succeed? Can we design probably approximately “safe” agents?