0a8620cf68595a4148fa80427fb7cd9d.ppt
- Количество слайдов: 104
 The Advanced Encryption Standard (Rijndael) Códigos y Criptografía Francisco Rodríguez Henríquez
The Advanced Encryption Standard (Rijndael) Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Why a new Standard? 1. Old standard insecure against brute-force attacks 2. Straightforward fixes lead to inefficient Triple DES 3. implementations 4. New trends in fast software encryption 1. use of basic instructions of the microprocessor 5. New ways of assessing cipher strength • differential cryptanalysis • linear cryptanalysis Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Why a new Standard? 1. Old standard insecure against brute-force attacks 2. Straightforward fixes lead to inefficient Triple DES 3. implementations 4. New trends in fast software encryption 1. use of basic instructions of the microprocessor 5. New ways of assessing cipher strength • differential cryptanalysis • linear cryptanalysis Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Why a Contest? • Speed-up the acceptance of the standard • Small number of specialists in the open research • Focus the effort of cryptographic community • Stimulate the research on methods of constructing • secure ciphers • Avoid backdoor theories Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Why a Contest? • Speed-up the acceptance of the standard • Small number of specialists in the open research • Focus the effort of cryptographic community • Stimulate the research on methods of constructing • secure ciphers • Avoid backdoor theories Códigos y Criptografía Francisco Rodríguez Henríquez
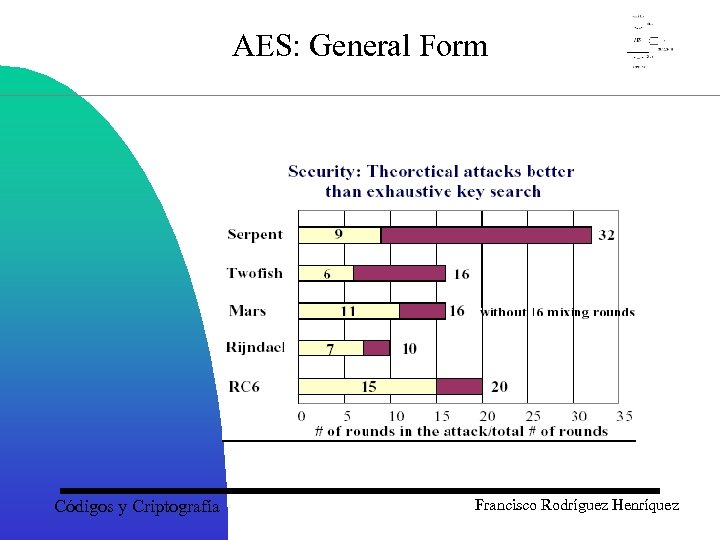 AES: General Form Códigos y Criptografía Francisco Rodríguez Henríquez
AES: General Form Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Rules of the Game Each team submits: • Detailed cipher description • Justification of design decisions • Tentative results of cryptanalysis • Source code in C • Source code in Java • Test vectors Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Rules of the Game Each team submits: • Detailed cipher description • Justification of design decisions • Tentative results of cryptanalysis • Source code in C • Source code in Java • Test vectors Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Candidates Round 1, June 1998: 15 Candidates from USA, Canada, Belgium, France, Germany, Norway, UK, Isreal, Korea, Japan, Australia, Costa Rica. Security, Software efficiency Round 2, August 1999: 5 final candidates Mars, RC 6, Rijndael, Serpent, Twofish Security, Hardware efficiency October 2000 1 winner: Rijndael Belgium Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Candidates Round 1, June 1998: 15 Candidates from USA, Canada, Belgium, France, Germany, Norway, UK, Isreal, Korea, Japan, Australia, Costa Rica. Security, Software efficiency Round 2, August 1999: 5 final candidates Mars, RC 6, Rijndael, Serpent, Twofish Security, Hardware efficiency October 2000 1 winner: Rijndael Belgium Códigos y Criptografía Francisco Rodríguez Henríquez
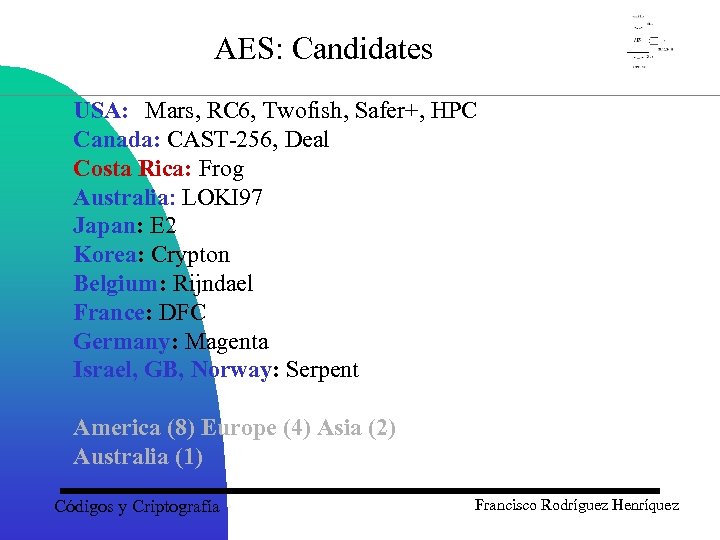 AES: Candidates USA: Mars, RC 6, Twofish, Safer+, HPC Canada: CAST-256, Deal Costa Rica: Frog Australia: LOKI 97 Japan: E 2 Korea: Crypton Belgium: Rijndael France: DFC Germany: Magenta Israel, GB, Norway: Serpent America (8) Europe (4) Asia (2) Australia (1) Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Candidates USA: Mars, RC 6, Twofish, Safer+, HPC Canada: CAST-256, Deal Costa Rica: Frog Australia: LOKI 97 Japan: E 2 Korea: Crypton Belgium: Rijndael France: DFC Germany: Magenta Israel, GB, Norway: Serpent America (8) Europe (4) Asia (2) Australia (1) Códigos y Criptografía Francisco Rodríguez Henríquez
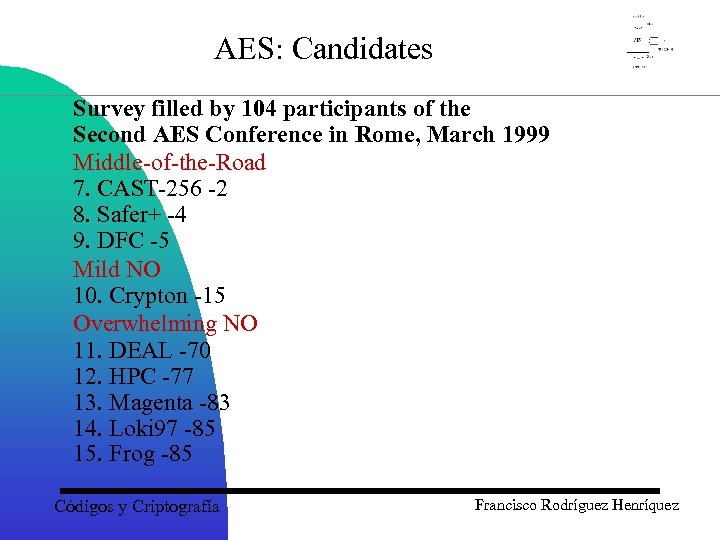 AES: Candidates Survey filled by 104 participants of the Second AES Conference in Rome, March 1999 Middle-of-the-Road 7. CAST-256 -2 8. Safer+ -4 9. DFC -5 Mild NO 10. Crypton -15 Overwhelming NO 11. DEAL -70 12. HPC -77 13. Magenta -83 14. Loki 97 -85 15. Frog -85 Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Candidates Survey filled by 104 participants of the Second AES Conference in Rome, March 1999 Middle-of-the-Road 7. CAST-256 -2 8. Safer+ -4 9. DFC -5 Mild NO 10. Crypton -15 Overwhelming NO 11. DEAL -70 12. HPC -77 13. Magenta -83 14. Loki 97 -85 15. Frog -85 Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Candidates Survey filled by 104 participants of the Second AES Conference in Rome, March 1999 Overwhelming YES: 1. Rijndael +76 2. RC 6 +73 3. Twofish +61 4. Mars +52 5. Serpent +45 Mild YES 6. E 2 +14 Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Candidates Survey filled by 104 participants of the Second AES Conference in Rome, March 1999 Overwhelming YES: 1. Rijndael +76 2. RC 6 +73 3. Twofish +61 4. Mars +52 5. Serpent +45 Mild YES 6. E 2 +14 Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Final 5 USA Mars - IBM C. Burwick, D. Coppersmith, E. D’Avignon, R. Gennaro, S. Halevi, C. Jutla, S. M. Matyas, L. O’Connor, M. Peyravian, D. Safford, N. Zunic RC 6 - RSA Data Security, Inc. R. Rivest - MIT M. Robshaw, R. Sidney, Y. L. Yin - RSA Twofish - Counterpane Systems B. Schneier, J. Kelsey, C. Hall, N. Ferguson - Counterpane, D. Whiting - Hi/fn, D. Wagner - Berkeley Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Final 5 USA Mars - IBM C. Burwick, D. Coppersmith, E. D’Avignon, R. Gennaro, S. Halevi, C. Jutla, S. M. Matyas, L. O’Connor, M. Peyravian, D. Safford, N. Zunic RC 6 - RSA Data Security, Inc. R. Rivest - MIT M. Robshaw, R. Sidney, Y. L. Yin - RSA Twofish - Counterpane Systems B. Schneier, J. Kelsey, C. Hall, N. Ferguson - Counterpane, D. Whiting - Hi/fn, D. Wagner - Berkeley Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Final 5 Europe Rijndael - J. Daemen, V. Rijmen Katholieke Universiteit Leuven Belgium Serpent - R. Anderson, Cambridge, England E. Biham - Technion, Israel L. Knudsen, University of Bergen, Norway AES Finalists (2) Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Final 5 Europe Rijndael - J. Daemen, V. Rijmen Katholieke Universiteit Leuven Belgium Serpent - R. Anderson, Cambridge, England E. Biham - Technion, Israel L. Knudsen, University of Bergen, Norway AES Finalists (2) Códigos y Criptografía Francisco Rodríguez Henríquez
 RC 6—The elegant AES choice Ron Rivest Matt Robshaw Yiqun Lisa Yin Códigos y Criptografía rivest@mit. edu mrobshaw@supanet. com yiqun@nttmcl. com Francisco Rodríguez Henríquez
RC 6—The elegant AES choice Ron Rivest Matt Robshaw Yiqun Lisa Yin Códigos y Criptografía rivest@mit. edu mrobshaw@supanet. com yiqun@nttmcl. com Francisco Rodríguez Henríquez
 RC 6 is the right AES choice • • • Security Performance Ease of implementation Simplicity Flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
RC 6 is the right AES choice • • • Security Performance Ease of implementation Simplicity Flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
![RC 6 is simple: only 12 lines B = B + S[ 0 ] RC 6 is simple: only 12 lines B = B + S[ 0 ]](https://present5.com/presentation/0a8620cf68595a4148fa80427fb7cd9d/image-14.jpg) RC 6 is simple: only 12 lines B = B + S[ 0 ] D = D + S[ 1 ] for i = 1 to 20 do { t = ( B x ( 2 B + 1 ) ) <<< 5 u = ( D x ( 2 D + 1 ) ) <<< 5 A = ( ( A t ) <<< u ) + S[ 2 i ] C = ( ( C u ) <<< t ) + S[ 2 i + 1 ] (A, B, C, D) = (B, C, D, A) } A = A + S[ 42 ] C = C + S[ 43 ] Códigos y Criptografía Francisco Rodríguez Henríquez
RC 6 is simple: only 12 lines B = B + S[ 0 ] D = D + S[ 1 ] for i = 1 to 20 do { t = ( B x ( 2 B + 1 ) ) <<< 5 u = ( D x ( 2 D + 1 ) ) <<< 5 A = ( ( A t ) <<< u ) + S[ 2 i ] C = ( ( C u ) <<< t ) + S[ 2 i + 1 ] (A, B, C, D) = (B, C, D, A) } A = A + S[ 42 ] C = C + S[ 43 ] Códigos y Criptografía Francisco Rodríguez Henríquez
 Simplicity • Facilitates and encourages analysis – allows rapid understanding of security – makes direct analysis straightforward (contrast with Mars and Twofish) • Enables easy implementation – allows compilers to produce high-quality code – obviates complicated optimizations – provides good performance with minimal effort Códigos y Criptografía Francisco Rodríguez Henríquez
Simplicity • Facilitates and encourages analysis – allows rapid understanding of security – makes direct analysis straightforward (contrast with Mars and Twofish) • Enables easy implementation – allows compilers to produce high-quality code – obviates complicated optimizations – provides good performance with minimal effort Códigos y Criptografía Francisco Rodríguez Henríquez
 RC 6 key schedule is rock-solid • Studied for more than six years • Secure – – thorough mixing one-way function no key separation (cf. Twofish) no related-key attacks (cf. Rijndael) Códigos y Criptografía Francisco Rodríguez Henríquez
RC 6 key schedule is rock-solid • Studied for more than six years • Secure – – thorough mixing one-way function no key separation (cf. Twofish) no related-key attacks (cf. Rijndael) Códigos y Criptografía Francisco Rodríguez Henríquez
 Original analysis still accurate • RC 6 meets original design criteria • Security estimates from 1998 still good today; independent analyses supportive. • Secure, even in theory, even with analysis improvements far beyond those seen for DES during its lifetime • RC 6 provides a solid, well-tuned margin for security Códigos y Criptografía Francisco Rodríguez Henríquez
Original analysis still accurate • RC 6 meets original design criteria • Security estimates from 1998 still good today; independent analyses supportive. • Secure, even in theory, even with analysis improvements far beyond those seen for DES during its lifetime • RC 6 provides a solid, well-tuned margin for security Códigos y Criptografía Francisco Rodríguez Henríquez
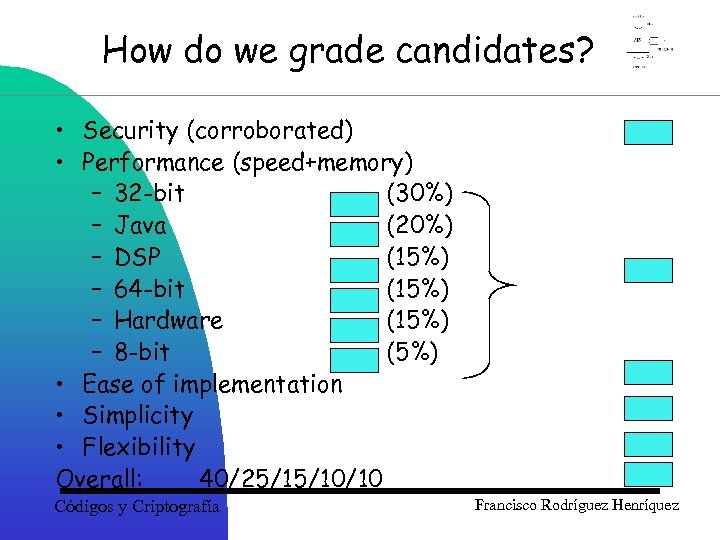 How do we grade candidates? • Security (corroborated) • Performance (speed+memory) – 32 -bit (30%) – Java (20%) – DSP (15%) – 64 -bit (15%) – Hardware (15%) – 8 -bit (5%) • Ease of implementation • Simplicity • Flexibility Overall: 40/25/15/10/10 Códigos y Criptografía Francisco Rodríguez Henríquez
How do we grade candidates? • Security (corroborated) • Performance (speed+memory) – 32 -bit (30%) – Java (20%) – DSP (15%) – 64 -bit (15%) – Hardware (15%) – 8 -bit (5%) • Ease of implementation • Simplicity • Flexibility Overall: 40/25/15/10/10 Códigos y Criptografía Francisco Rodríguez Henríquez
 Conclusions • RC 6 is a simple yet remarkably strong cipher – – – good performance on most important platforms simple to code for good performance excellent flexibility the most studied finalist the best understood finalist • RC 6 is the secure and “elegant” choice for the AES Códigos y Criptografía Francisco Rodríguez Henríquez
Conclusions • RC 6 is a simple yet remarkably strong cipher – – – good performance on most important platforms simple to code for good performance excellent flexibility the most studied finalist the best understood finalist • RC 6 is the secure and “elegant” choice for the AES Códigos y Criptografía Francisco Rodríguez Henríquez
 (The End) Códigos y Criptografía Francisco Rodríguez Henríquez
(The End) Códigos y Criptografía Francisco Rodríguez Henríquez
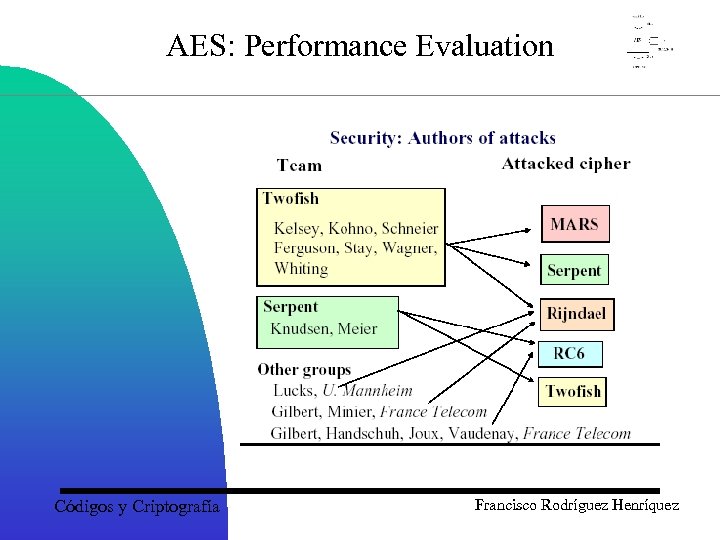 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
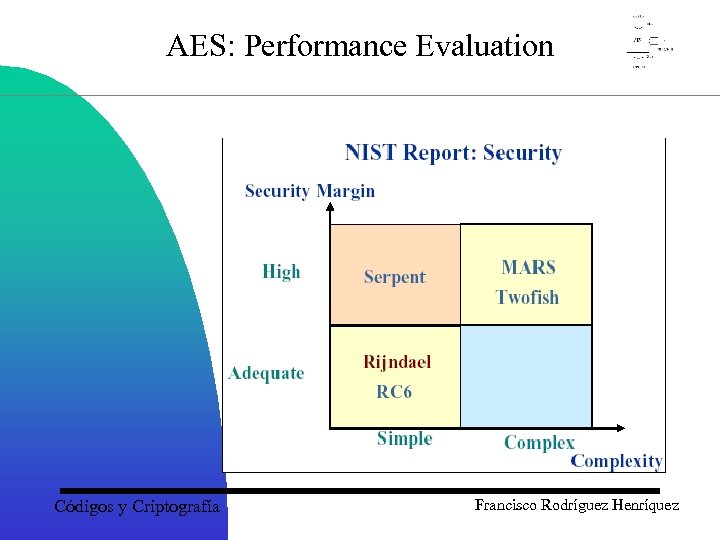 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
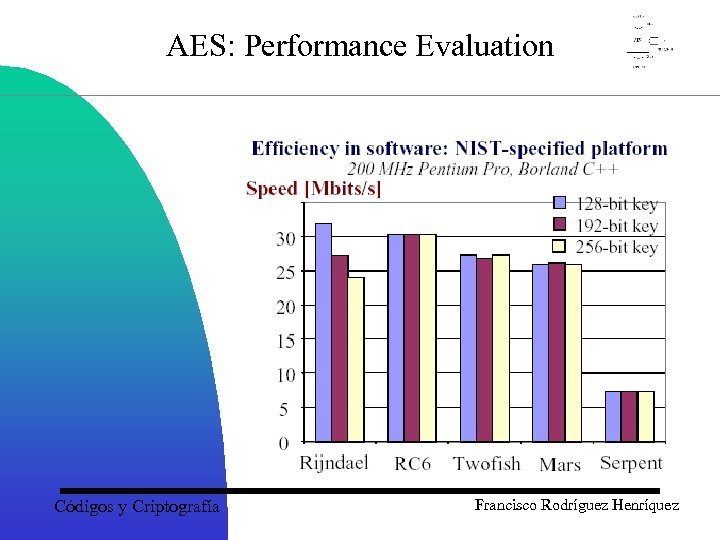 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
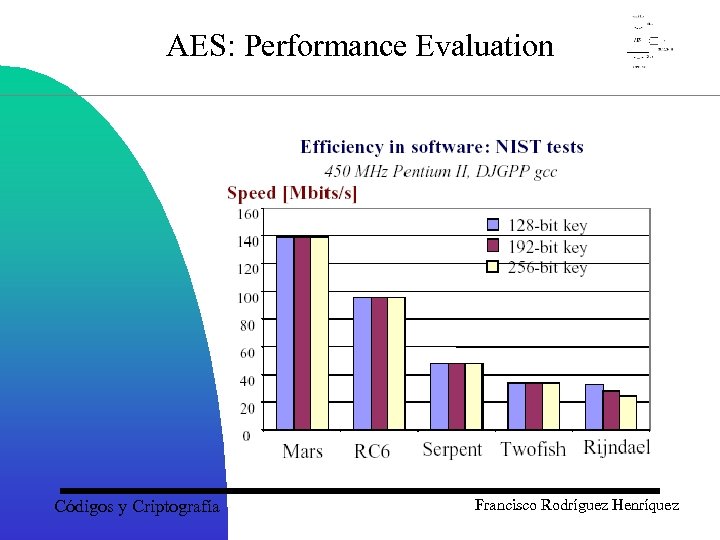 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
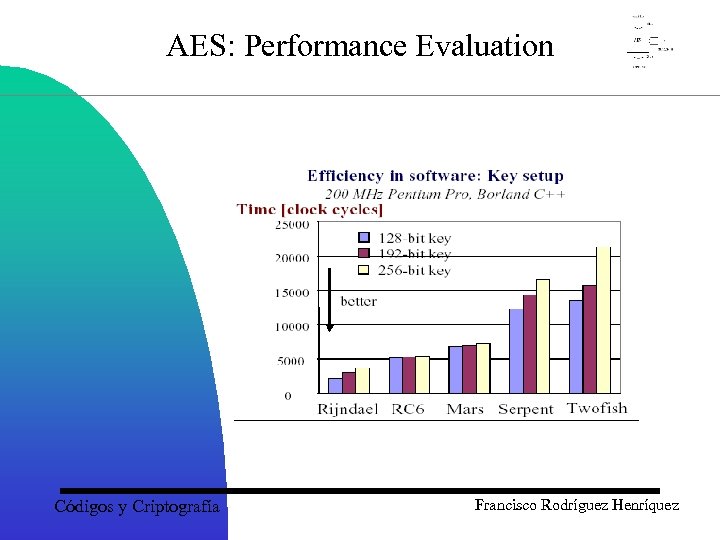 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
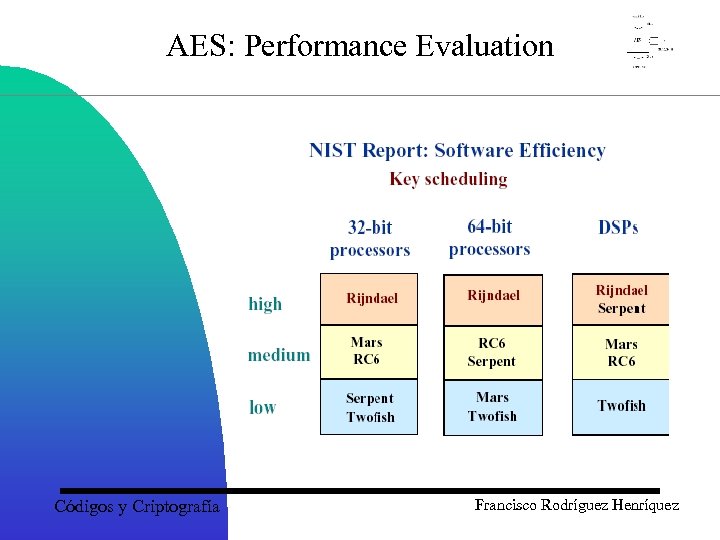 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
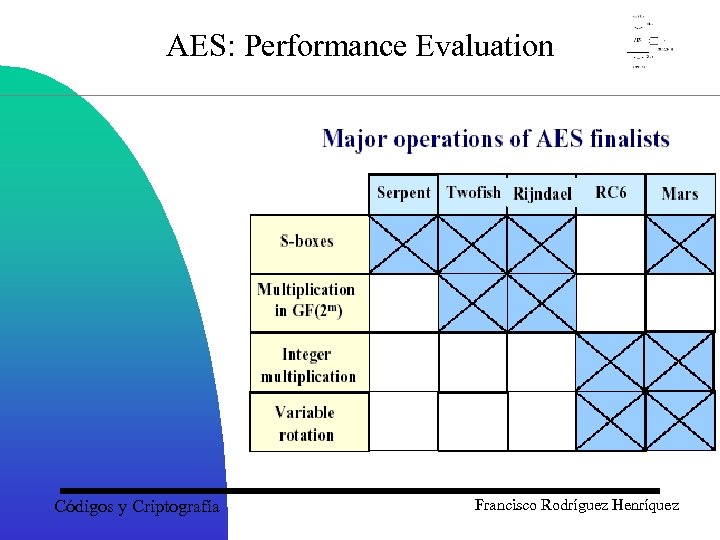 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
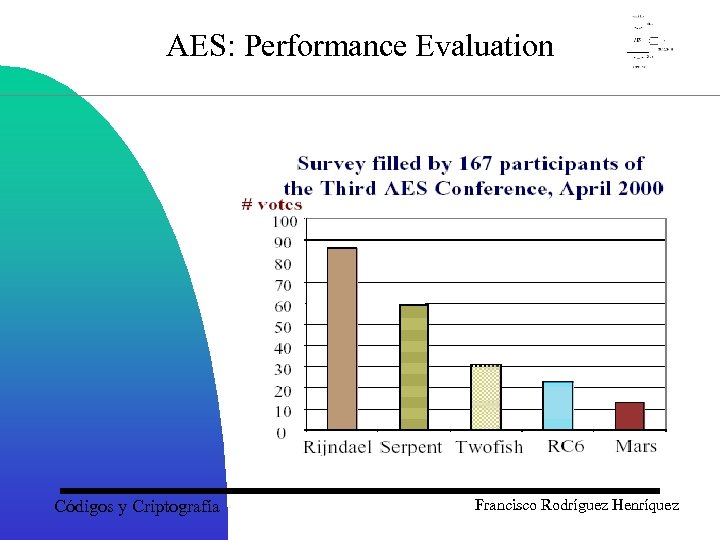 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Performance Evaluation Códigos y Criptografía Francisco Rodríguez Henríquez
![AES: Summary of Final-5 Evaluation Serpent [2] Pluses: • large security margin • cryptanalytical AES: Summary of Final-5 Evaluation Serpent [2] Pluses: • large security margin • cryptanalytical](https://present5.com/presentation/0a8620cf68595a4148fa80427fb7cd9d/image-35.jpg) AES: Summary of Final-5 Evaluation Serpent [2] Pluses: • large security margin • cryptanalytical reputation of authors • conservative construction • very fast in hardware Minuses: • slow in software • moderate flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Summary of Final-5 Evaluation Serpent [2] Pluses: • large security margin • cryptanalytical reputation of authors • conservative construction • very fast in hardware Minuses: • slow in software • moderate flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
![AES: Summary of Final-5 Evaluation Rijndael [1] Pluses: • fastest in hardware • close AES: Summary of Final-5 Evaluation Rijndael [1] Pluses: • fastest in hardware • close](https://present5.com/presentation/0a8620cf68595a4148fa80427fb7cd9d/image-36.jpg) AES: Summary of Final-5 Evaluation Rijndael [1] Pluses: • fastest in hardware • close to the fastest in software • security margin • novel ideas • very high flexibility Minuses: • security margin Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Summary of Final-5 Evaluation Rijndael [1] Pluses: • fastest in hardware • close to the fastest in software • security margin • novel ideas • very high flexibility Minuses: • security margin Códigos y Criptografía Francisco Rodríguez Henríquez
 AES: Summary of Final-5 Evaluation Twofish Pluses: • good security margin • fast encryption/decryption in software • US • strongly advertized Minuses: • moderately fast in hardware • slow key setup in software • moderate flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
AES: Summary of Final-5 Evaluation Twofish Pluses: • good security margin • fast encryption/decryption in software • US • strongly advertized Minuses: • moderately fast in hardware • slow key setup in software • moderate flexibility Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View • Designed by Joan Daemen and Vincent Rijmen (from Leuven Belgium) • Based upon the Square Cipher • 3 Design Goals: 1. Resistance against known attacks 2. Speed and code compactness on a variety of platforms 3. Design simplicity Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View • Designed by Joan Daemen and Vincent Rijmen (from Leuven Belgium) • Based upon the Square Cipher • 3 Design Goals: 1. Resistance against known attacks 2. Speed and code compactness on a variety of platforms 3. Design simplicity Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View ¥ Rijndael/AES Designed by: Joan Daemen, Proton World International Vincent Rijmen, Katholique Universiteit Lueven Block cypher Symmetric key Arithmetic based in the Galois Field GF(28) Fast and scalable Resistant to all known cryptanalysis attacks Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View ¥ Rijndael/AES Designed by: Joan Daemen, Proton World International Vincent Rijmen, Katholique Universiteit Lueven Block cypher Symmetric key Arithmetic based in the Galois Field GF(28) Fast and scalable Resistant to all known cryptanalysis attacks Códigos y Criptografía Francisco Rodríguez Henríquez
 Dr. Vincent Rijmen Códigos y Criptografía Francisco Rodríguez Henríquez
Dr. Vincent Rijmen Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael • The block cipher Rijndael is designed to use only simple whole-byte operations. Also, it provides extra flexibility over that required of an AES candidate, in that both the key size and the block size may be chosen to be any of 128, 192, or 256 bits. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael • The block cipher Rijndael is designed to use only simple whole-byte operations. Also, it provides extra flexibility over that required of an AES candidate, in that both the key size and the block size may be chosen to be any of 128, 192, or 256 bits. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View • Rijndael is not a Feistel cipher 3 distinct invertible layers per round Encryption and decryption algorithms are different • Rijndael uses the Wide Trail Strategy 1. Non-linear layer (confusion) 2. Linear mixing layer (diffusion) 3. Key addition layer Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View • Rijndael is not a Feistel cipher 3 distinct invertible layers per round Encryption and decryption algorithms are different • Rijndael uses the Wide Trail Strategy 1. Non-linear layer (confusion) 2. Linear mixing layer (diffusion) 3. Key addition layer Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View • State and Round Key representations • The State is the intermediate cipher result • Both the State and the Round Key are interpreted as rectangular arrays of bytes • Number of columns in the State and Round Key arrays depend on block and key sizes, respectively Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View • State and Round Key representations • The State is the intermediate cipher result • Both the State and the Round Key are interpreted as rectangular arrays of bytes • Number of columns in the State and Round Key arrays depend on block and key sizes, respectively Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View • Rijndael is a block cipher that encrypts and decrypts 128, 192, and 256 bit blocks, using 128, 192, and 256 byte keys in any combination. The block is considered to be structured as 4, 6, or 8 columns of 4 bytes, depending on block size. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View • Rijndael is a block cipher that encrypts and decrypts 128, 192, and 256 bit blocks, using 128, 192, and 256 byte keys in any combination. The block is considered to be structured as 4, 6, or 8 columns of 4 bytes, depending on block size. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael • During an early stage of the AES process, a draft version of the requirements would have required each algorithm to have three versions, with both the key and block sizes equal to each of 128, 192, and 256 bits. This was later changed to make three required versions have those three key sizes, but only a block size of 128 bits, which is more easily accommodated by many types of block cipher design. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael • During an early stage of the AES process, a draft version of the requirements would have required each algorithm to have three versions, with both the key and block sizes equal to each of 128, 192, and 256 bits. This was later changed to make three required versions have those three key sizes, but only a block size of 128 bits, which is more easily accommodated by many types of block cipher design. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael • The original description of Rijndael is available at: http: //www. esat. kuleuven. ac. be/~rijmen/rijndael/. • However, the variations of Rijndael which act on larger block sizes apparently will not be included in the actual standard, on the basis that the cryptanalytic study of Rijndael during the standards process primarily focused on the version with the 128 -bit block size. • Rijndael is a relatively simple cipher in many respects. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael • The original description of Rijndael is available at: http: //www. esat. kuleuven. ac. be/~rijmen/rijndael/. • However, the variations of Rijndael which act on larger block sizes apparently will not be included in the actual standard, on the basis that the cryptanalytic study of Rijndael during the standards process primarily focused on the version with the 128 -bit block size. • Rijndael is a relatively simple cipher in many respects. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Number of Rounds • Rijndael has a variable number of rounds. The number of rounds in Rijndael is: 1. 10 if both the block and the key are 128 bits long. 2. 12 if either the block or the key is 192 bits long, and neither of them is longer than that. 3. 14 if either the block or the key is 256 bits long. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Number of Rounds • Rijndael has a variable number of rounds. The number of rounds in Rijndael is: 1. 10 if both the block and the key are 128 bits long. 2. 12 if either the block or the key is 192 bits long, and neither of them is longer than that. 3. 14 if either the block or the key is 256 bits long. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View Each round consists of 4 steps • Step 1: Byte. Sub Transformation (Confusion) • Step 2: Shift. Row Transformation (Diffusion) • Step 3: Mix. Column Transformation (Diffusion) • Step 4: Round Key Addition • Final round slightly different from other rounds Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View Each round consists of 4 steps • Step 1: Byte. Sub Transformation (Confusion) • Step 2: Shift. Row Transformation (Diffusion) • Step 3: Mix. Column Transformation (Diffusion) • Step 4: Round Key Addition • Final round slightly different from other rounds Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View The basic operations applied to the block are: 1) Byte. Sub: Applying an S-box (substituting each byte with another, based on an equation in GF(2^8)); 2) Shift. Row: Shifting the rows in a circular way, the amount of shift (0, 1, 2, 3, or 4 bytes) depending on the position from the top and on the block size, Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View The basic operations applied to the block are: 1) Byte. Sub: Applying an S-box (substituting each byte with another, based on an equation in GF(2^8)); 2) Shift. Row: Shifting the rows in a circular way, the amount of shift (0, 1, 2, 3, or 4 bytes) depending on the position from the top and on the block size, Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Over. View 3) Mix. Column: Mixing the 4, 6, or 8 columns vertically by taking invertible linear combinations (in GF(2^8) of the elements in each column and; 4) Round Key Addition: XORing each byte with a round key (done before the first round for “whitening, ” and again at the end of each round), Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Over. View 3) Mix. Column: Mixing the 4, 6, or 8 columns vertically by taking invertible linear combinations (in GF(2^8) of the elements in each column and; 4) Round Key Addition: XORing each byte with a round key (done before the first round for “whitening, ” and again at the end of each round), Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Algorithm – Rijndael Cypher. AES(data_block, key) {in State, Round. Keys State xor Round. Key 0 for Round = 1 to Nr Sub. Bytes(State) Shift. Row (State) If not(last Round) then Mix. Column(State) State xor Round. Key. Round out State } Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Algorithm – Rijndael Cypher. AES(data_block, key) {in State, Round. Keys State xor Round. Key 0 for Round = 1 to Nr Sub. Bytes(State) Shift. Row (State) If not(last Round) then Mix. Column(State) State xor Round. Key. Round out State } Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Sequence of Operations • The extra final round omits the Mix Column step, but is otherwise the same as a regular round. Thus, the sequence of steps in Rijndael is: ARK BSB, SR, MC, ARK; . . . BSB, SR, MC, ARK; BSB, SR, ARK; Códigos y Criptografía 9 of them!! Francisco Rodríguez Henríquez
Rijndael: Sequence of Operations • The extra final round omits the Mix Column step, but is otherwise the same as a regular round. Thus, the sequence of steps in Rijndael is: ARK BSB, SR, MC, ARK; . . . BSB, SR, MC, ARK; BSB, SR, ARK; Códigos y Criptografía 9 of them!! Francisco Rodríguez Henríquez
 Rijndael: Sequence of Operations Where: ARK = Add Round Key BSB = Byte Sub Block SR = Shift Row MC = Mix Column Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Sequence of Operations Where: ARK = Add Round Key BSB = Byte Sub Block SR = Shift Row MC = Mix Column Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael Códigos y Criptografía Francisco Rodríguez Henríquez
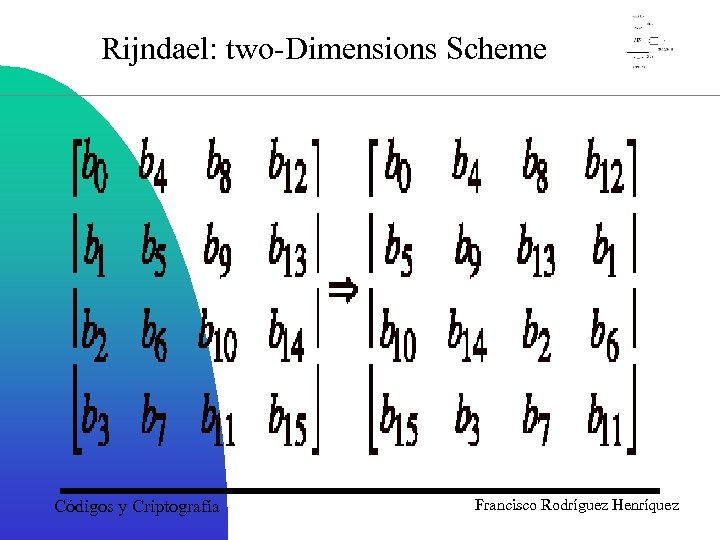 Rijndael: two-Dimensions Scheme Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: two-Dimensions Scheme Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Block Representation Rijndael considers a 128 -bit block grouped into 16 bytes of 8 bits each. Let us call each of these 16 bytes as, b 15 b 14 b 13… b 2 b 1 b 0. Rijndael deals with this block as bytes arranged into a 4*4 matrix, Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Block Representation Rijndael considers a 128 -bit block grouped into 16 bytes of 8 bits each. Let us call each of these 16 bytes as, b 15 b 14 b 13… b 2 b 1 b 0. Rijndael deals with this block as bytes arranged into a 4*4 matrix, Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Round’s Steps • In the Byte Sub step each byte of the block is replaced by its substitute in an S-box. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Round’s Steps • In the Byte Sub step each byte of the block is replaced by its substitute in an S-box. Códigos y Criptografía Francisco Rodríguez Henríquez
 S-Box: Look-up Table method • Write a byte as 8 bits: x 7 x 6 x 5 x 4 x 3 x 2 x 1 x 0. Look for the entry in the x 7 x 6 x 5 x 4 row and x 3 x 2 x 1 x 0 column. Códigos y Criptografía Francisco Rodríguez Henríquez
S-Box: Look-up Table method • Write a byte as 8 bits: x 7 x 6 x 5 x 4 x 3 x 2 x 1 x 0. Look for the entry in the x 7 x 6 x 5 x 4 row and x 3 x 2 x 1 x 0 column. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: S-Box 99 124 119 123 242 107 111 197 48 1 103 43 254 215 171 118 202 130 201 125 250 89 71 240 173 212 162 175 156 164 114 192 183 253 147 38 54 63 247 204 52 165 229 241 113 216 49 21 4 199 35 195 24 150 5 154 7 18 128 226 235 39 178 117 9 131 44 26 27 110 90 160 82 59 214 179 41 227 47 132 83 209 0 237 32 252 177 91 106 203 190 57 74 76 88 207 208 239 170 251 67 77 51 133 69 249 2 127 80 60 159 168 81 163 64 143 146 157 56 245 188 182 218 33 16 255 243 210 205 12 19 236 95 151 68 23 196 167 126 61 100 93 25 115 96 129 79 220 34 42 144 136 70 238 184 20 222 94 11 219 224 50 58 10 73 6 36 92 194 211 172 98 145 149 228 121 231 200 55 109 141 213 78 169 108 86 244 234 101 122 174 8 186 120 37 46 28 166 180 198 232 221 116 31 75 189 138 112 62 181 102 72 3 246 14 97 53 87 185 134 193 29 158 225 248 152 17 105 217 142 148 155 30 135 233 206 85 40 223 140 161 137 13 191 230 66 104 65 153 45 15 176 84 187 22 Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: S-Box 99 124 119 123 242 107 111 197 48 1 103 43 254 215 171 118 202 130 201 125 250 89 71 240 173 212 162 175 156 164 114 192 183 253 147 38 54 63 247 204 52 165 229 241 113 216 49 21 4 199 35 195 24 150 5 154 7 18 128 226 235 39 178 117 9 131 44 26 27 110 90 160 82 59 214 179 41 227 47 132 83 209 0 237 32 252 177 91 106 203 190 57 74 76 88 207 208 239 170 251 67 77 51 133 69 249 2 127 80 60 159 168 81 163 64 143 146 157 56 245 188 182 218 33 16 255 243 210 205 12 19 236 95 151 68 23 196 167 126 61 100 93 25 115 96 129 79 220 34 42 144 136 70 238 184 20 222 94 11 219 224 50 58 10 73 6 36 92 194 211 172 98 145 149 228 121 231 200 55 109 141 213 78 169 108 86 244 234 101 122 174 8 186 120 37 46 28 166 180 198 232 221 116 31 75 189 138 112 62 181 102 72 3 246 14 97 53 87 185 134 193 29 158 225 248 152 17 105 217 142 148 155 30 135 233 206 85 40 223 140 161 137 13 191 230 66 104 65 153 45 15 176 84 187 22 Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Round’s Steps • The specification for Rijndael only provided an explanation of how the S-box was calculated: the first step was to replace each byte with its reciprocal in the same GF(28) as used below in the Mix Column step, except that 0, which has no reciprocal, is replaced by itself (since it isn't anything's reciprocal either, it is the only value not used, so that makes sense) then a bitwise modulo-two matrix multiply was used, and finally the hexadecimal number 63 is XORed with the result. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Round’s Steps • The specification for Rijndael only provided an explanation of how the S-box was calculated: the first step was to replace each byte with its reciprocal in the same GF(28) as used below in the Mix Column step, except that 0, which has no reciprocal, is replaced by itself (since it isn't anything's reciprocal either, it is the only value not used, so that makes sense) then a bitwise modulo-two matrix multiply was used, and finally the hexadecimal number 63 is XORed with the result. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Byte. Sub Step ¥ ¥ S-Box Arithmetic. Elements in G : = GF(28, 1+a+a 3+a 4+a 8 ) nhex Þ nbin Þ (polynomial with nÕs bits for coeffs) Arithmetic in Z 2 (+/*), then mod by 1+a+a 3+a 4+a 8 polynomial Þ nbin Þ nhex Byte. Sub(x) = A « Mx-1 + 63 hex Precompute and use look-up table Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Byte. Sub Step ¥ ¥ S-Box Arithmetic. Elements in G : = GF(28, 1+a+a 3+a 4+a 8 ) nhex Þ nbin Þ (polynomial with nÕs bits for coeffs) Arithmetic in Z 2 (+/*), then mod by 1+a+a 3+a 4+a 8 polynomial Þ nbin Þ nhex Byte. Sub(x) = A « Mx-1 + 63 hex Precompute and use look-up table Códigos y Criptografía Francisco Rodríguez Henríquez
 The Construction of the S-Box • Although the S-box is implemented as a lookup table, it has a simple mathematical description. • Start with a byte x 7 x 6 x 5 x 4 x 3 x 2 x 1 x 0, where each xi is a binary bit. Compute its inverse in GF(28). If the byte is 0, use the same 0 as its inverse. Códigos y Criptografía Francisco Rodríguez Henríquez
The Construction of the S-Box • Although the S-box is implemented as a lookup table, it has a simple mathematical description. • Start with a byte x 7 x 6 x 5 x 4 x 3 x 2 x 1 x 0, where each xi is a binary bit. Compute its inverse in GF(28). If the byte is 0, use the same 0 as its inverse. Códigos y Criptografía Francisco Rodríguez Henríquez
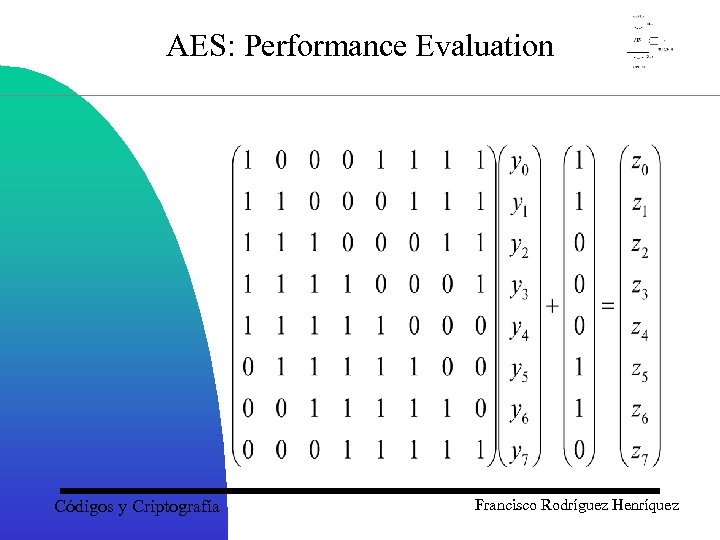
 The Construction of the S-Box • The resulting byte y 7 y 6 y 5 y 4 y 3 y 2 y 1 y 0 represents an 8 -dimensional column vector, with the rightmost bit y 0 in the top position. Multiply by a matrix and add the column vector (1, 1, 0, 0, 1, 1, 0) to obtain a vector z 7 z 6 z 5 z 4 z 3 z 2 z 1 z 0 as shown in the next slide: Códigos y Criptografía Francisco Rodríguez Henríquez
The Construction of the S-Box • The resulting byte y 7 y 6 y 5 y 4 y 3 y 2 y 1 y 0 represents an 8 -dimensional column vector, with the rightmost bit y 0 in the top position. Multiply by a matrix and add the column vector (1, 1, 0, 0, 1, 1, 0) to obtain a vector z 7 z 6 z 5 z 4 z 3 z 2 z 1 z 0 as shown in the next slide: Códigos y Criptografía Francisco Rodríguez Henríquez
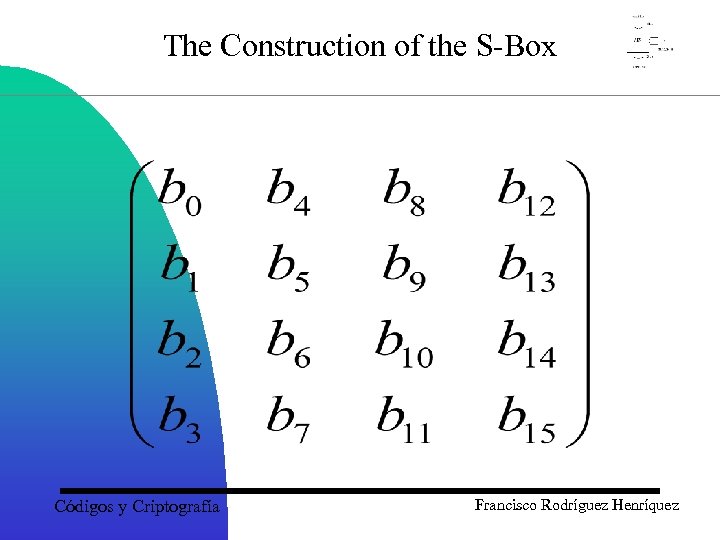 The Construction of the S-Box Códigos y Criptografía Francisco Rodríguez Henríquez
The Construction of the S-Box Códigos y Criptografía Francisco Rodríguez Henríquez
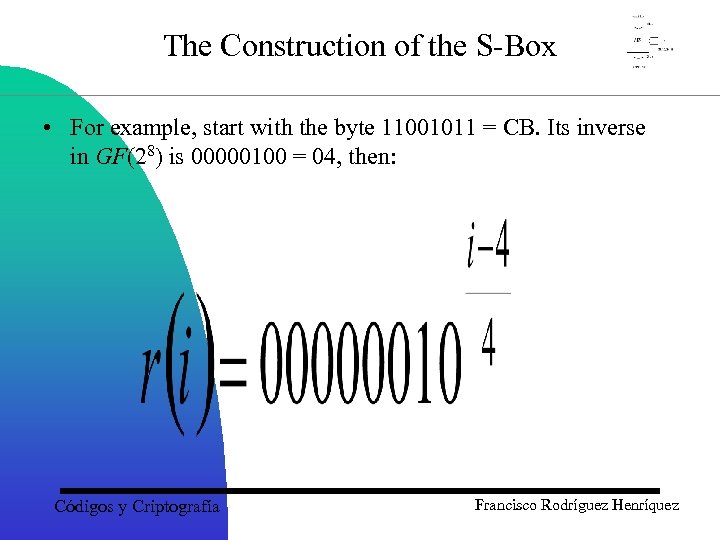 The Construction of the S-Box • For example, start with the byte 11001011 = CB. Its inverse in GF(28) is 00000100 = 04, then: Códigos y Criptografía Francisco Rodríguez Henríquez
The Construction of the S-Box • For example, start with the byte 11001011 = CB. Its inverse in GF(28) is 00000100 = 04, then: Códigos y Criptografía Francisco Rodríguez Henríquez
 The Construction of the S-Box • This yields the byte 00011111 = 1 F. Note that the input vector was 11001011. The 4 MSBs of the input vector are thus 1100 and this gives us the 13 th row in the S-Box. Similarly, 1011 yields us the 14 th column in the S-Box. By checking the S-box we see that indeed 31 = 1 F is the corresponding entry in the SBox as claimed. Códigos y Criptografía Francisco Rodríguez Henríquez
The Construction of the S-Box • This yields the byte 00011111 = 1 F. Note that the input vector was 11001011. The 4 MSBs of the input vector are thus 1100 and this gives us the 13 th row in the S-Box. Similarly, 1011 yields us the 14 th column in the S-Box. By checking the S-box we see that indeed 31 = 1 F is the corresponding entry in the SBox as claimed. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Shift Row Step Next is the Shift Row step. Considering the 128 -bit block grouped into 16 bytes of 8 bits each, call them, b 15 b 14 b 13… b 2 b 1 b 0. these bytes are arranged into a 4*4 matrix, and shifted as follows: Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Shift Row Step Next is the Shift Row step. Considering the 128 -bit block grouped into 16 bytes of 8 bits each, call them, b 15 b 14 b 13… b 2 b 1 b 0. these bytes are arranged into a 4*4 matrix, and shifted as follows: Códigos y Criptografía Francisco Rodríguez Henríquez
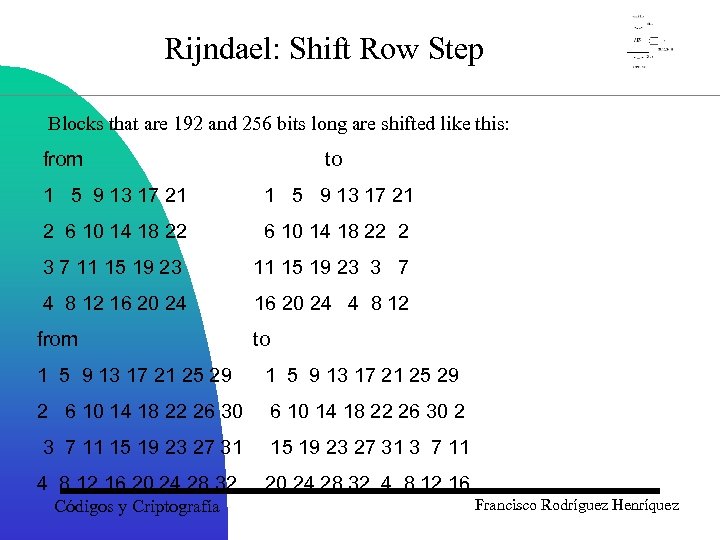 Rijndael: Shift Row Step Blocks that are 192 and 256 bits long are shifted like this: from to 1 5 9 13 17 21 2 6 10 14 18 22 2 3 7 11 15 19 23 3 7 4 8 12 16 20 24 4 8 12 from to 1 5 9 13 17 21 25 29 2 6 10 14 18 22 26 30 2 3 7 11 15 19 23 27 31 3 7 11 4 8 12 16 20 24 28 32 4 8 12 16 Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Shift Row Step Blocks that are 192 and 256 bits long are shifted like this: from to 1 5 9 13 17 21 2 6 10 14 18 22 2 3 7 11 15 19 23 3 7 4 8 12 16 20 24 4 8 12 from to 1 5 9 13 17 21 25 29 2 6 10 14 18 22 26 30 2 3 7 11 15 19 23 27 31 3 7 11 4 8 12 16 20 24 28 32 4 8 12 16 Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Mix Column step • Next comes the Mix Column step. Matrix multiplication is performed: each column, in the arrangement we have seen above, is multiplied by the matrix: 2311 1231 1123 3112 • However, this multiplication is done over GF(28). This means that the bytes being multiplied are treated as polynomials rather than numbers. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Mix Column step • Next comes the Mix Column step. Matrix multiplication is performed: each column, in the arrangement we have seen above, is multiplied by the matrix: 2311 1231 1123 3112 • However, this multiplication is done over GF(28). This means that the bytes being multiplied are treated as polynomials rather than numbers. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Mix Column step • GF(28)The Galois Field with 28 elements is the Finite Field GF(28)=Z 2[x]/m(x) where m is irreducible in Z 2[x] and has degree 8. Rijndael chooses m(x) = 1 + x 3 + x 4 + x 8 Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Mix Column step • GF(28)The Galois Field with 28 elements is the Finite Field GF(28)=Z 2[x]/m(x) where m is irreducible in Z 2[x] and has degree 8. Rijndael chooses m(x) = 1 + x 3 + x 4 + x 8 Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Mix Column step • If the result has more than 8 bits, the extra bits are not simply discarded: instead, they're cancelled out by XORing the binary 9 -bit string 100011011 with the result (shifted right if necessary). This string stands for the generating polynomial of the particular version of GF(2^8) used by Rijndael. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Mix Column step • If the result has more than 8 bits, the extra bits are not simply discarded: instead, they're cancelled out by XORing the binary 9 -bit string 100011011 with the result (shifted right if necessary). This string stands for the generating polynomial of the particular version of GF(2^8) used by Rijndael. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Mix Column step For example, multiplying the binary string 11001010 by 3 within this Galois Field works like this: 11001010 11 -------11001010 -------101011110 (XOR instead of addition) 100011011 (this is XORed, instead of subt. 256) -------1000101 Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Mix Column step For example, multiplying the binary string 11001010 by 3 within this Galois Field works like this: 11001010 11 -------11001010 -------101011110 (XOR instead of addition) 100011011 (this is XORed, instead of subt. 256) -------1000101 Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Mix Column step Mix. Column Arithmetic. Mix. Column is equivalent to with arithmetic in GF( 28 ). Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Mix Column step Mix. Column Arithmetic. Mix. Column is equivalent to with arithmetic in GF( 28 ). Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Add Round Key The final step is Add Round Key. This simply XORs in the subkey for the current round. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Add Round Key The final step is Add Round Key. This simply XORs in the subkey for the current round. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule Round keys extracted from the cipher key in two steps: 1. Initial key expansion • First bits of the expanded key are set to the bits of the cipher key • Remaining bits calculated recursively as a non-linear function of the previous bits of the expanded key 2. Round key selection from expanded key Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule Round keys extracted from the cipher key in two steps: 1. Initial key expansion • First bits of the expanded key are set to the bits of the cipher key • Remaining bits calculated recursively as a non-linear function of the previous bits of the expanded key 2. Round key selection from expanded key Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • The original key consists of 128 bits, which are arranged into a 4*4 matrix of bytes. This matrix is expanded by adjoining 40 more columns, as follows. • Label the first four columns W(0), W(1), W(2), W(3). The new columns are generated recursively. Suppose columns up through W(i-1) have been defined. If i is not a multiple of 4, then form the new column as, W(i) = W(i-4) W(i-1). Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • The original key consists of 128 bits, which are arranged into a 4*4 matrix of bytes. This matrix is expanded by adjoining 40 more columns, as follows. • Label the first four columns W(0), W(1), W(2), W(3). The new columns are generated recursively. Suppose columns up through W(i-1) have been defined. If i is not a multiple of 4, then form the new column as, W(i) = W(i-4) W(i-1). Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • If i is a multiple of 4, then W(i) = W(i-4) T(W(i-1)), Where T(W(i-1)) is the transformation of W(i-1) as follows. Let the elements of the columns are w 0 w 1 w 2 w 3. Shift these cyclically to obtain w 1 w 2 w 3 w 0. Then replace each of these bytes with the corresponding element in the Sbox from the Byte. Sub step, to get 4 bytes y 0 y 1 y 2 y 3. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • If i is a multiple of 4, then W(i) = W(i-4) T(W(i-1)), Where T(W(i-1)) is the transformation of W(i-1) as follows. Let the elements of the columns are w 0 w 1 w 2 w 3. Shift these cyclically to obtain w 1 w 2 w 3 w 0. Then replace each of these bytes with the corresponding element in the Sbox from the Byte. Sub step, to get 4 bytes y 0 y 1 y 2 y 3. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • Finally compute the round constant In GF(28). Recall that we are in the case where i is a multiple of 4. Then T(W(i-1)) is the column vector (y 0 r(i), y 1 y 2 y 3) Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • Finally compute the round constant In GF(28). Recall that we are in the case where i is a multiple of 4. Then T(W(i-1)) is the column vector (y 0 r(i), y 1 y 2 y 3) Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • In this way, columns W(4), …, W(43) are generated from the initial four columns. The round key for the ith round consists of the columns: W(4 i), W(4 i+1), W(4 i+2), W(4 i+3. ) Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • In this way, columns W(4), …, W(43) are generated from the initial four columns. The round key for the ith round consists of the columns: W(4 i), W(4 i+1), W(4 i+2), W(4 i+3. ) Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • Because it begins and ends with an ARK (Add Round Key) step, there is no wasted unkeyed step at the beginning or end. The sequence of operations is important for facilitating decipherment, as well. • Although the sequence is not symmetrical, the order of some of the steps in Rijndael could be changed without affecting the cipher. The Byte Sub step could just as easily be done after the Shift Row step as before it. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • Because it begins and ends with an ARK (Add Round Key) step, there is no wasted unkeyed step at the beginning or end. The sequence of operations is important for facilitating decipherment, as well. • Although the sequence is not symmetrical, the order of some of the steps in Rijndael could be changed without affecting the cipher. The Byte Sub step could just as easily be done after the Shift Row step as before it. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • For keys 128 and 192 bits in length, the subkey material, which consists of all the round keys in order, consists of the original key, followed by stretches, each the length of the original key, consisting of four-byte words such that each word is the XOR of the preceding four-byte word and either the corresponding word in the previous stretch or a function of it. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • For keys 128 and 192 bits in length, the subkey material, which consists of all the round keys in order, consists of the original key, followed by stretches, each the length of the original key, consisting of four-byte words such that each word is the XOR of the preceding four-byte word and either the corresponding word in the previous stretch or a function of it. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Key Schedule • For the first word in a stretch, the word is first rotated one byte to the left, and then its bytes are transformed using the S-box from the Byte Sub step, and then a round-dependent constant is XORed to its first byte. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • For the first word in a stretch, the word is first rotated one byte to the left, and then its bytes are transformed using the S-box from the Byte Sub step, and then a round-dependent constant is XORed to its first byte. Códigos y Criptografía Francisco Rodríguez Henríquez
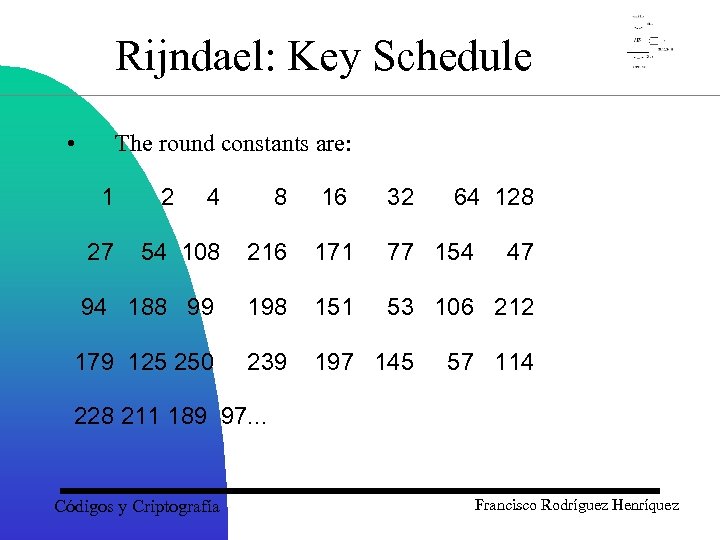 Rijndael: Key Schedule • The round constants are: 1 4 8 16 32 54 108 216 171 77 154 94 188 99 198 151 53 106 212 179 125 250 239 197 145 27 2 64 128 47 57 114 228 211 189 97. . . Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Key Schedule • The round constants are: 1 4 8 16 32 54 108 216 171 77 154 94 188 99 198 151 53 106 212 179 125 250 239 197 145 27 2 64 128 47 57 114 228 211 189 97. . . Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption Inverse Cypher: • Reverse Steps • Use Keys in Reverse Order • Byte. Sub and Shift. Row Commute • Mix. Column Matrix is Invertible Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption Inverse Cypher: • Reverse Steps • Use Keys in Reverse Order • Byte. Sub and Shift. Row Commute • Mix. Column Matrix is Invertible Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 1. The inverse of Byte. Sub is another lookup table, called Inv. Byte. Sub. 2. The inverse of Shift. Row is obtained by shifting the rows to the right instead of to the left, yielding Inv. Shift. Row. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 1. The inverse of Byte. Sub is another lookup table, called Inv. Byte. Sub. 2. The inverse of Shift. Row is obtained by shifting the rows to the right instead of to the left, yielding Inv. Shift. Row. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 3. The inverse of Mix. Column exists because the 4*4 matrix used in Mix. Column is invertible. The transformation Inv. Mix. Column is given by multiplication by the matrix Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 3. The inverse of Mix. Column exists because the 4*4 matrix used in Mix. Column is invertible. The transformation Inv. Mix. Column is given by multiplication by the matrix Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Sequence of Operations for Encryption • The extra final round omits the Mix Column step, but is otherwise the same as a regular round. Thus, the sequence of steps in Rijndael is: ARK BSB, SR, MC, ARK; . . . BSB, SR, MC, ARK; BSB, SR, ARK; Códigos y Criptografía 9 of them!! Francisco Rodríguez Henríquez
Rijndael: Sequence of Operations for Encryption • The extra final round omits the Mix Column step, but is otherwise the same as a regular round. Thus, the sequence of steps in Rijndael is: ARK BSB, SR, MC, ARK; . . . BSB, SR, MC, ARK; BSB, SR, ARK; Códigos y Criptografía 9 of them!! Francisco Rodríguez Henríquez
 Rijndael: Sequence of Operations Where: ARK = Add Round Key BSB = Byte Sub Block SR = Shift Row MC = Mix Column Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Sequence of Operations Where: ARK = Add Round Key BSB = Byte Sub Block SR = Shift Row MC = Mix Column Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 4. Add. Round. Key is its own inverse. Hence to decrypt we have to perform the following steps: ARK, ISR, IBS ARK, IMC, ISR, IBS; . . . ARK, IMC, ISR, IBS; ARK; Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 4. Add. Round. Key is its own inverse. Hence to decrypt we have to perform the following steps: ARK, ISR, IBS ARK, IMC, ISR, IBS; . . . ARK, IMC, ISR, IBS; ARK; Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 1. However, we would like to rewrite this decryption in order to make it look more like encryption. We make the following observations: I. The order of BS and the SR operations are exchangable (why? ? ). II. We also would like to reverse the order of ARK and IMC but this is not possible. Instead we proceed as follows: Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 1. However, we would like to rewrite this decryption in order to make it look more like encryption. We make the following observations: I. The order of BS and the SR operations are exchangable (why? ? ). II. We also would like to reverse the order of ARK and IMC but this is not possible. Instead we proceed as follows: Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 1. Where (mi, j) is the 4*4 matrix in Mix. Column and (ki, j) is the round key matrix. The inverse is obtained by solving for (ci, j) in terms of (ei, j), namely, Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 1. Where (mi, j) is the 4*4 matrix in Mix. Column and (ki, j) is the round key matrix. The inverse is obtained by solving for (ci, j) in terms of (ei, j), namely, Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption Therefore the decryption process to follow is: The first arrow is simply Inv. Mix. Column applied to (ei, j). If we let Inv. Add. Round. Key be XORing with (k’i, j), then we have that the inverse of “MC then ARK” is “IMC then IARK”. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption Therefore the decryption process to follow is: The first arrow is simply Inv. Mix. Column applied to (ei, j). If we let Inv. Add. Round. Key be XORing with (k’i, j), then we have that the inverse of “MC then ARK” is “IMC then IARK”. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption We now see that decryption is given by: ARK, IBS, ISR IMC, IARK, IBS, ISR; . . . IMC, IARK, IBS, ISR; ARK. Summarizing we have the following procedures to perform encryption/decryption with Rijndael algorithm: Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption We now see that decryption is given by: ARK, IBS, ISR IMC, IARK, IBS, ISR; . . . IMC, IARK, IBS, ISR; ARK. Summarizing we have the following procedures to perform encryption/decryption with Rijndael algorithm: Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Encryption 1. ARK using the 0 th key. 2. Nine rounds of BS, SR, MC, ARK using round keys 1 to 9. 3. A final round: BS, SR, ARK, using the 10 th round key. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Encryption 1. ARK using the 0 th key. 2. Nine rounds of BS, SR, MC, ARK using round keys 1 to 9. 3. A final round: BS, SR, ARK, using the 10 th round key. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Decryption 1. ARK using the 10 th key. 2. Nine rounds of IBS, ISR, IMC, IARK using round keys 9 to 1. 3. A final round: IBS, ISR, ARK, using the 0 th round key. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Decryption 1. ARK using the 10 th key. 2. Nine rounds of IBS, ISR, IMC, IARK using round keys 9 to 1. 3. A final round: IBS, ISR, ARK, using the 0 th round key. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Why Mix. Column is omitted in the last round? 1. Suppose Mix. Column had been left in. Then the encryption would start ARK, BS, SR, MC, ARK, …, and it would end ARK, BS, SR, MC, ARK. Therefore, the beginning o fthe decryption would be (after the reorderings) IMC, IARK, IBS, ISR, …. This means the decryption would have an unnecessary IMC at the beginning. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Why Mix. Column is omitted in the last round? 1. Suppose Mix. Column had been left in. Then the encryption would start ARK, BS, SR, MC, ARK, …, and it would end ARK, BS, SR, MC, ARK. Therefore, the beginning o fthe decryption would be (after the reorderings) IMC, IARK, IBS, ISR, …. This means the decryption would have an unnecessary IMC at the beginning. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Why Mix. Column is omitted in the last round? 1. Another way to look at encryption is that there is an initial. ARK, then a sequence of alternating half rounds (BS, SR), (MC, ARK), (BS, SR), …, (MC, ARK), (BS, SR), followed by a final ARK. 1. The decryption is ARK, followed by a sequence of alternating half rounds: (IBS, ISR), (IMC, IARK), (IBS, ISR), …, (IMC, IARK), (IBS, ISR) Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Why Mix. Column is omitted in the last round? 1. Another way to look at encryption is that there is an initial. ARK, then a sequence of alternating half rounds (BS, SR), (MC, ARK), (BS, SR), …, (MC, ARK), (BS, SR), followed by a final ARK. 1. The decryption is ARK, followed by a sequence of alternating half rounds: (IBS, ISR), (IMC, IARK), (IBS, ISR), …, (IMC, IARK), (IBS, ISR) Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: Why Mix. Column is omitted in the last round? 1. Followed by a final ARK. From this point of view, we see that a final MC would not fit naturally into any of the half rounds, and it results natural to leave it out. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: Why Mix. Column is omitted in the last round? 1. Followed by a final ARK. From this point of view, we see that a final MC would not fit naturally into any of the half rounds, and it results natural to leave it out. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. On 8 -bit processors, decryption is not quite as fast as encryption. This is because the entriesof the 4*4 matrix for Inv. Mix. Column are more complex than those for Mix. Column, and this is enough to make decryption take around 30% longer than encryption for those processors. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. On 8 -bit processors, decryption is not quite as fast as encryption. This is because the entriesof the 4*4 matrix for Inv. Mix. Column are more complex than those for Mix. Column, and this is enough to make decryption take around 30% longer than encryption for those processors. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. The fact that encryption and decryption are not identical processes leads to the expectation that there are no weak keys in Rijndael, in contrast to DES and several other algorithms. 2. In Rijndael all the bits are treated uniformly. This has the effect of diffusing the input bits faster. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. The fact that encryption and decryption are not identical processes leads to the expectation that there are no weak keys in Rijndael, in contrast to DES and several other algorithms. 2. In Rijndael all the bits are treated uniformly. This has the effect of diffusing the input bits faster. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. It can be shown that two rounds are enough to obtain full difussion, namely, each of the 128 output bits depends on each of the 128 input bits. 2. The Rijndael S-box is highly nonlinear, since it is based on the mapping x x-1 in GF(28). This means that Rijndael is excellent resisting differential and linear cryptoanalysis attacks. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. It can be shown that two rounds are enough to obtain full difussion, namely, each of the 128 output bits depends on each of the 128 input bits. 2. The Rijndael S-box is highly nonlinear, since it is based on the mapping x x-1 in GF(28). This means that Rijndael is excellent resisting differential and linear cryptoanalysis attacks. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. The Shift. Row step was added to resist two recently developed attacks, namely truncated differentials and the Square attack (Square is a predecessor of Rijndael). 2. The Mix. Column causes diffusion among the bytes. A change in one input byte in this step always results in all four output bytes changing. If two input bytes are changed, at least three output bytes are changed. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. The Shift. Row step was added to resist two recently developed attacks, namely truncated differentials and the Square attack (Square is a predecessor of Rijndael). 2. The Mix. Column causes diffusion among the bytes. A change in one input byte in this step always results in all four output bytes changing. If two input bytes are changed, at least three output bytes are changed. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. The Key Schedule involves nonlinear mixing of the key bits, since it uses the S-box. The mixing is designed to resist attacks where the cryptoanalyst knows part of the key and tries to deduce the remaining bits. 2. The round constants are used to eliminate symmetries in the encryption process by making each round different. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. The Key Schedule involves nonlinear mixing of the key bits, since it uses the S-box. The mixing is designed to resist attacks where the cryptoanalyst knows part of the key and tries to deduce the remaining bits. 2. The round constants are used to eliminate symmetries in the encryption process by making each round different. Códigos y Criptografía Francisco Rodríguez Henríquez
 Rijndael: SOme design consideration comments. 1. The number of rounds was chosen to be 10 because there attacks that are better than brute force up to six rounds. 2. No known attack beats brute force for seven or more rounds. 3. It was felt that four extra rounds provide a large enough margin of safety. Of course, the number of rounds could easily be increased if needed. Códigos y Criptografía Francisco Rodríguez Henríquez
Rijndael: SOme design consideration comments. 1. The number of rounds was chosen to be 10 because there attacks that are better than brute force up to six rounds. 2. No known attack beats brute force for seven or more rounds. 3. It was felt that four extra rounds provide a large enough margin of safety. Of course, the number of rounds could easily be increased if needed. Códigos y Criptografía Francisco Rodríguez Henríquez


