Техническая теория изгиба пластин Пластинками будем называть

Техническая теория изгиба пластин

Пластинками будем называть тела призматической или цилиндрической формы, у которых один размер (толщина) мал по сравнению с другими размерами. R z y x h срединная плоскость h << R

Классификация пластинок В зависимости от вида напряженного состояния пластинки классифицируется так: 1) Q Очень тонкие пластинки – мембраны, в ней возникают осевые усилия N, а изгиб. моментов и поперечных сил нет: М=0; Q=0. N 2) Пластинки средней толщины – плиты. N – толщина – размер в плане

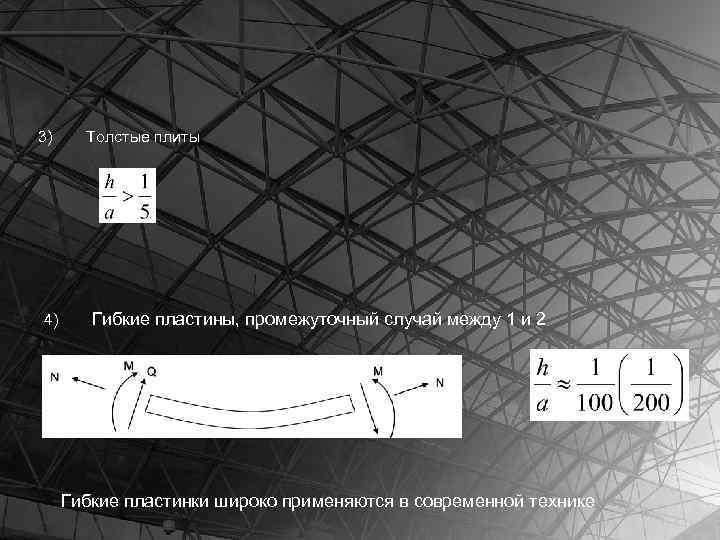
3) 4) Толстые плиты Гибкие пластины, промежуточный случай между 1 и 2 Гибкие пластинки широко применяются в современной технике

Упрощающие гипотезы теории пластин средней толщины 1) Гипотеза: При изгибе пластинки её толщина не меняется, а плоскости, параллельные серединной плоскости, друг на друга не давят. 2) Гипотеза Кирхгофа о прямолинейном нормальном элементе: Всякое плоское до деформации вертикальное сечение пластины остаётся плоским и после деформации, поэтому сдвиговые деформации в плоскостях X 0 Z и Y 0 Z отсутствуют. m n

3) Гипотеза: При изгибе пластинки отсутствуют тангенциальные перемещения в её срединной плоскости (при z=0, Следствия из введённых гипотез: 1) 2) u=v=0).

Используя 3 гипотезу, получим: Таким образом после введения 3 -х упрощающих гипотез, мы видим, что вместо 3 -х неизвестных функций U, V, W осталась одна неизвестная функция – прогиб пластинки W, которая не содержит переменной z (не зависит от z). Далее будем рассматривать срединную плоскость пластинки.

ВЫВОД ФОРМУЛ ДЛЯ ИЗГИБАЮЩИХ И КРУТЯЩЕГО МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ. dx=1 dy=1 – элементарный момент X z h dz Y – изгибающий момент

EJ – жёсткость при изгибе балки h 1 – цилиндрическая пластинки жёсткость изгиба

R – равнодействующая 1 H – крутящий момент 1 h/2 X z z dz Y h/2 R

ВЫВОД УРАВНЕНИЯ РАВНОВЕСИЯ ДЛЯ ЭЛЕМЕНТАРНОЙ ЧАСТИ ПЛАСТИНЫ

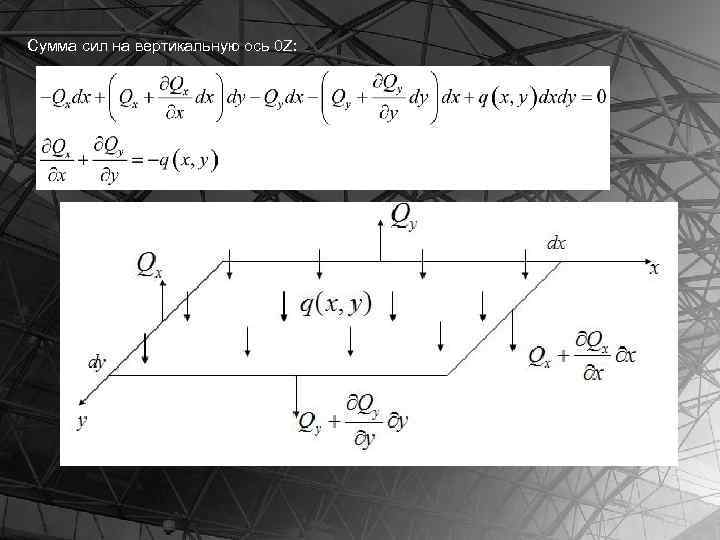
Сумма сил на вертикальную ось 0 Z:

- Уравнение Софи Жермен-Лагранжа - основное дифференциальное уравнение изгиба пластинки, обычно записываемое в виде:

Таким образом, расчёт любой пластинки сводится к решению ур-ния Софи Жермен при заданных граничных условиях (услов. закреп. её краёв): • – прогиб пластинки, – изгибающий момент • – перерезывающая сила • H – крутящий момент • W – угол поворота - обобщенные поперечные силы Кирхгофа

Виды граничных условий x n 1. Край пластинки шарнир опёрт y n 1. Край пластинки шарнир опёрт n 2. Край пластинки жёстко защёмлён n 3. Край свободен от закрепления

Классификация граничных условий Граничные условия бывают геометрическими, статическими и смешанными. – геометрические граничные условия – статические граничные условия Граничные условия подразделяют на однородные и неоднородные. Схема подхода к решению задач прочности пластины. • • Анализ конструкции Расчётная схема Математическая модель Численная реализация математической модели

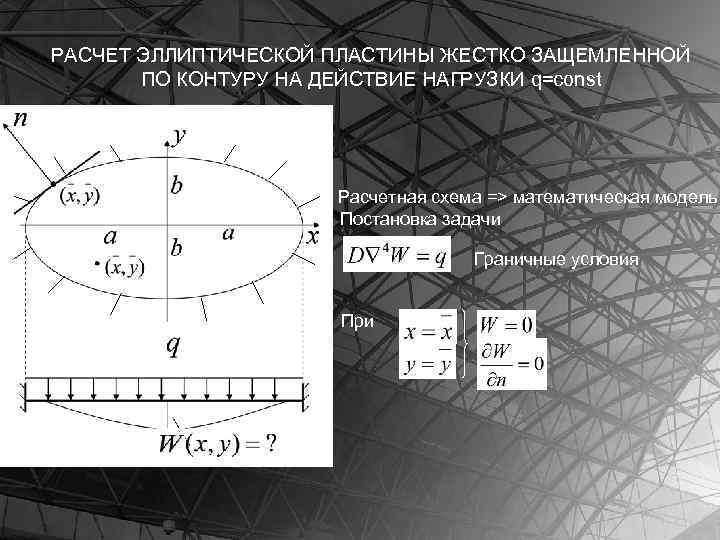
РАСЧЕТ ЭЛЛИПТИЧЕСКОЙ ПЛАСТИНЫ ЖЕСТКО ЗАЩЕМЛЕННОЙ ПО КОНТУРУ НА ДЕЙСТВИЕ НАГРУЗКИ q=const Расчетная схема => математическая модель Постановка задачи Граничные условия При

Уравнение эллипса: Прогиб будем искать в виде: Проверим выполняются ли граничные условия: Углы поворота в точке контура Таком образом выбранный нами прогиб удовлетворяет граничным условиям при любом значении неизвестного коэффициента с Выбранный прогиб подставим в уравнение Софи Жермен-Лагранжа.

- точное решение для эллиптической пластинки - точное решение для круглой пластины - прогиб в центре

РАСЧЕТ ПРЯМОУГОЛЬНЫХ ПЛАСТИН, ШАРНИРНО ОПЕРТЫХ ПО ВСЕМУ КОНТУРУ, НА ДЕЙСТВИЕ ПРОИЗВОЛЬНОЙ НАГРУЗКИ Математическая модель при Произвольную нагрузку разложим в двойной ряд по синусам:

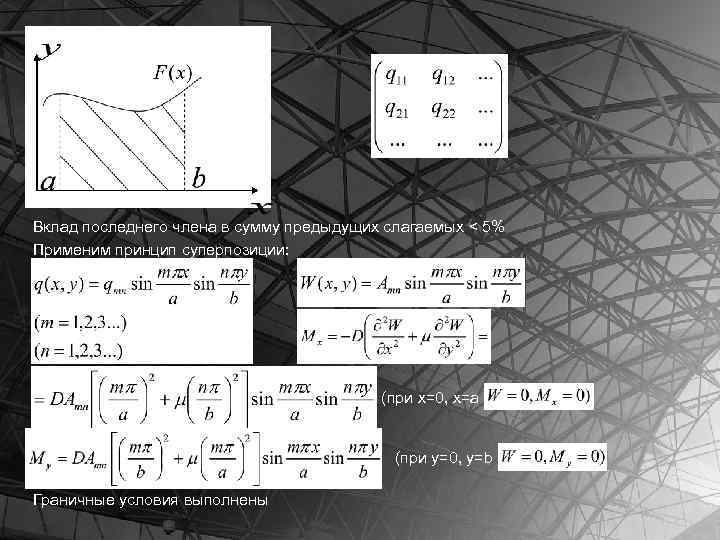
Вклад последнего члена в сумму предыдущих слагаемых < 5% Применим принцип суперпозиции: (при x=0, x=a (при y=0, y=b Граничные условия выполнены

Выбранный нами прогиб удовлетворяет заданным граничным условиям при любом значении неизвестного коэффициента Выбранный прогиб подставим в уравнение Софи Жермен-Лагранжа Это выражение является равенством, если значения перед синусами в левой и правой частях равны

Даем m и n последовательно значения 1, 2, 3… и вычисляем - параметр удлинения пластинки - точное решение Вспомним принцип суперпозиции Точное решение задачи в незамкнутой форме Этот метод разработал Навье

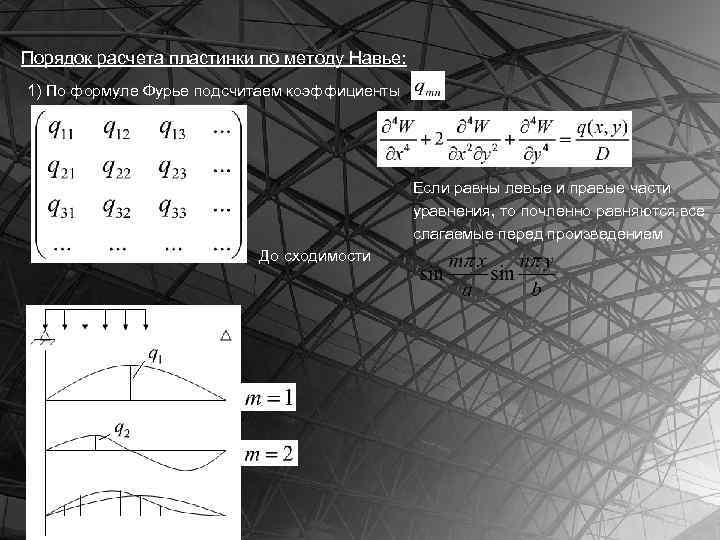
Порядок расчета пластинки по методу Навье: 1) По формуле Фурье подсчитаем коэффициенты Если равны левые и правые части уравнения, то почленно равняются все cлагаемые перед произведением До сходимости

2) Подсчитаем коэффициенты 3) Подсчитаем прогиб 4) Подсчитываем изгибающие и крутящий моменты 5) Строим эпюры W, 6) Подсчитываем наибольшие напряжения и путем сопоставления их с нормативными напряжениями находим допускаемый уровень нагрузки q(x, y) на пластинку.

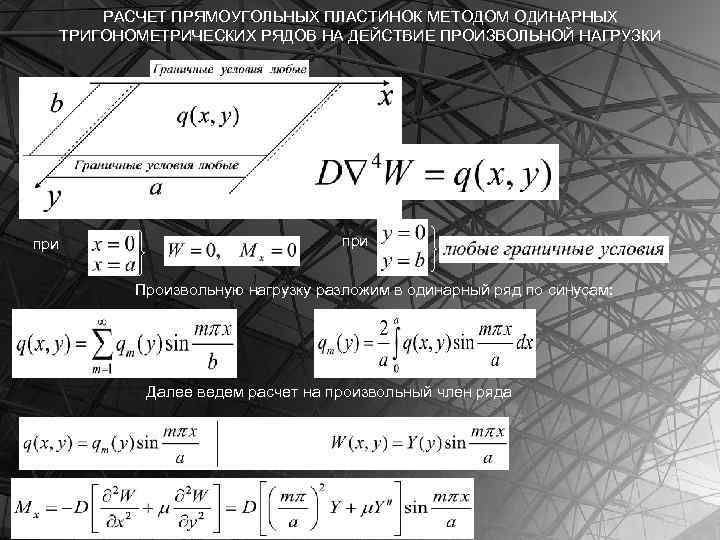
РАСЧЕТ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК МЕТОДОМ ОДИНАРНЫХ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ НА ДЕЙСТВИЕ ПРОИЗВОЛЬНОЙ НАГРУЗКИ Математическая модель при Произвольную нагрузку разложим в одинарный ряд по синусам: Далее ведем расчет на произвольный член ряда

Непосредственной подстановкой убеждаемся, что заданные граничные условия при этом выполняется точно при любом виде неизвестной функции Y(y) Возьмем Y(y) и подставим в уравнение Софи Жермен-Лагранжа Данное равенство справедливо тогда и только тогда, когда выражения перед синусами равны:

Таким образом, выбранный нами прогиб будет решением поставленной задачи, если функция Y(y) будет решением этого обыкновенного неоднородного Дифференциального уравнения с постоянными коэффициентами - действительные, сопряженные, кратные корни

Получено решение задачи на произвольный член ряда. Применим принцип суперпозиции: Получено решение для заданной исходной нагрузки. Этот метод называют методом Мориса Леви Распишем граничные условия:

Суммируя решения на конкретные слагаемые рядов разложения нагрузки, получим: Сходимость решения зависит от двух факторов: 1) Плавности изменения нагрузки по направлениям осей X и Y в пластинке; 2) От величины параметра удлиненности пластинки. 1. Численные эксперименты показывают, что скорость сходимости решения краевой задачи изгиба пластинки по методу Леви существенно выше, чем по методу двойных тригонометрических рядов Навье. 2. Область применения метода Леви больше, чем метода Навье.

Построение аппроксимирующих функций статическим методом В. З. Власова В. З. Власов (1906 -1958 г. г. ) предложил способ построения функций распределения прогиба пластины, удовлетворяющих как граничным условиям, так и характеру распределения внешней нагрузки. К входным параметрам относятся: a, b, h (м)-(1, 2, 3), толщина пластины; E(Па), μ(безр)- (4, 5), условие закрепления (6, 7, 8, 9); q(x, y) (10) (при расчете в размерном виде) Σ 10

При решении в безразмерном виде решению соответствует бесконечное множество пластин для любых значений а(м), h(м), Е(Па) Далее рассчитываем пластинку в безразмерном виде: По алгоритму статического метода В. З. Власова необходимо: 1. Вырезаем из пластинки полоску по одному направлению 2. Рассматриваем данную полоску как обыкновенную балку Дифференциальное уравнение изгиба балки имеет вид: В безразмерном виде: (1)

Кроме того используются граничные условия: ; Необходимо получить выражение y(η) и для ее производной. Интегрируем выражение (1): ; => ; ; Используем граничные условия для нахождения С 1, С 2, С 3, С 4: y(0)=0: 0+0+С 4 =0 => С 4=0 y. I(0)=0: 0+0+0+C 3=0 => C 3=0 Используем граничные условия на правом конце балки для подсчета величин С 1 и С 2: ; ;

Подставляя полученные значения: - -точное решение для балки, но приближенное решение для пластинки, по направле Амплитуда прогиба пластинки не связана с амплитудой прогиба балки и затем буде найдена из решения задачи по одному из методов. В проведенный характер изменения прогиба пластинки по направлению оси η. Т. е. для дальнейших расчетов применим: