cfa6658056889ba9d1aa85ed71bd992a.ppt
- Количество слайдов: 11

Testing the Hilbert space dimension Nicolas Brunner, Nicolas Gisin, André Méthot GAP-Optique (Geneva) Valerio Scarani National University of Singapore (Singapore) Stefano Pironio, Antonio Acín ICFO-Institut de Ciències Fotòniques (Barcelona) MATHQCI, Madrid, May 2008
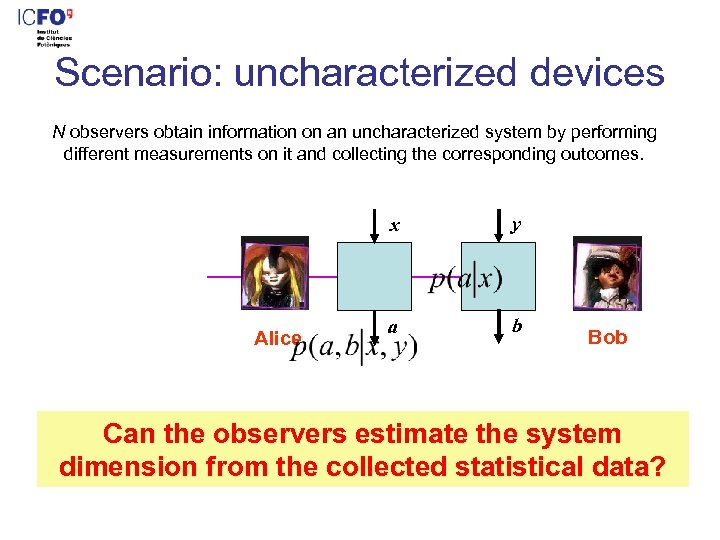
Scenario: uncharacterized devices N observers obtain information on an uncharacterized system by performing different measurements on it and collecting the corresponding outcomes. x Alice y a b Bob Can the observers estimate the system dimension from the collected statistical data?

Motivation • Quantum Information Theory: necessary resources for attaining some quantum correlations (Navascués’ talk). • Quantum Information Theory with uncharacterized devices. Device-Independent protocols (Scarani’s talk). • Standard QKD: the honest parties know the Hilbert space dimension. Is this an experimentally testable assumption? • Fundamental viewpoint: is it possible to measure the dimension of a physical system?

Quantum Information Viewpoint Classical resources are free. • Single observer: the statistical data can always be reproduced by classical means. • N > 1 observers: if the data have a local model, one has: The correlations are achievable by means of classically correlated instructions. No quantum resource is needed for the generation. In this scenario, the problem is non-trivial only for non-local correlations, i. e. correlations violating a Bell inequality.

Dimension witnesses Def. 1: Some correlations p(a, b|x, y) have a d-dimensional representation if where while is a quantum state acting on a composite d x d dimensional space, and define local measurements on each space. Def. 2: A d-dimensional witness is linear function on the correlations, described a vector of real coefficients such that: (i) for all d-dimensional quantum correlations while (ii) for some quantum correlations. Dimension Witness Q(d) Q
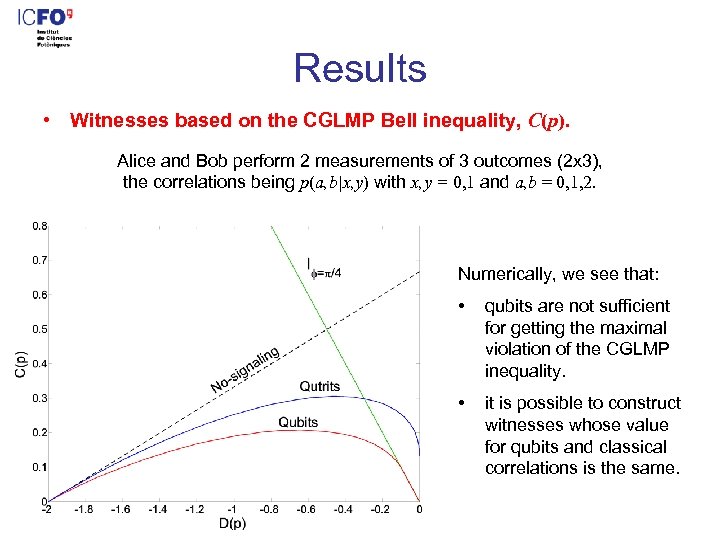
Results • Witnesses based on the CGLMP Bell inequality, C(p). Alice and Bob perform 2 measurements of 3 outcomes (2 x 3), the correlations being p(a, b|x, y) with x, y = 0, 1 and a, b = 0, 1, 2. Numerically, we see that: • qubits are not sufficient for getting the maximal violation of the CGLMP inequality. • it is possible to construct witnesses whose value for qubits and classical correlations is the same.

Results • Reducing the “trinity”: simpler qubit witnesses. It is perhaps not surprising that the maximal quantum violation of a three-outcome Bell inequality is not attained by qubits. Measurement scenario: All correlations are Are all correlations attainable by qubits? attainable by qubits (Tsirelson & Masanes) 2 x 2 2 measurement of 2 outcomes 3 x 2 1 x 3 New example of qubit witness

Results • Qubit witnesses from measurements of 2 outcomes. Correlators: Classical value: C(i, j) quantum ↔ Quantum value: Qubit value: Since KG(3) < KG , there exist two-outcome quantum correlations not achievable measuring qubits. The proof is not constructive. Gill’s question: there exist d-outcome quantum correlations not achievable by measuring d-dimensional systems (Perez-García et al. & Vertesi and Pal). Conjecture: there are witnesses for any dimension with 2 -outcome measurements.

Concluding remarks • Estimating the dimension of a quantum system is a very general problem that deserves further investigation. Dimension witnesses represent one of the first steps in this direction. • In our scenario, classical resources are free, we focus on the minimal quantum dimension. • The distinction between classical and quantum degrees of freedom is less natural when dealing with more fundamental issues. • How to estimate the dimension of a single system? • Is the set of d-dimensional correlations convex? • Can the set of quantum correlations of m measurements of n outcomes be generated by means of finite-dimensional systems?
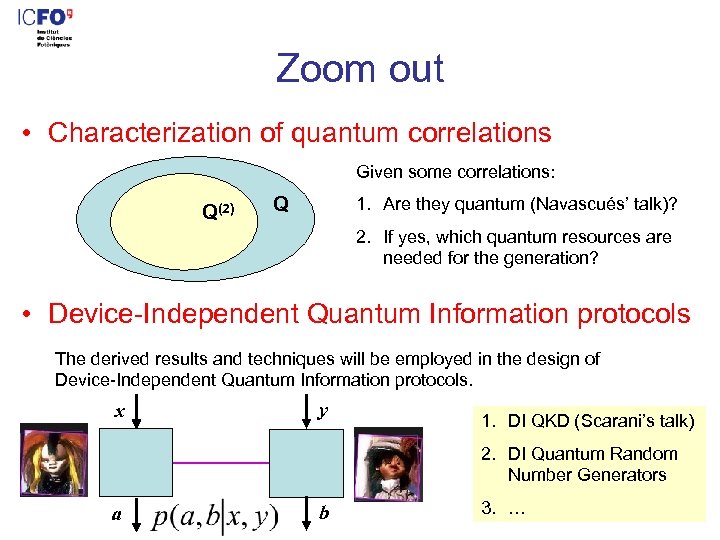
Zoom out • Characterization of quantum correlations Given some correlations: Q(2) Q 1. Are they quantum (Navascués’ talk)? 2. If yes, which quantum resources are needed for the generation? • Device-Independent Quantum Information protocols The derived results and techniques will be employed in the design of Device-Independent Quantum Information protocols. x y 1. DI QKD (Scarani’s talk) 2. DI Quantum Random Number Generators a b 3. …

for ks an Th n! tio ten at our y N. Brunner, S. Pironio, A. Acin, N. Gisin, A. Methot and V. Scarani ar. Xiv: 0802. 0760, to appear in Phys. Rev. Lett.
cfa6658056889ba9d1aa85ed71bd992a.ppt