Test of Homogeneity Lecture 45 Section 14 4

Test of Homogeneity Lecture 45 Section 14. 4 Wed, Apr 19, 2006

Homogeneous Populations Two distributions are called homogeneous if they exhibit the same proportions within categories. n For example, if two colleges’ student bodies are each 55% female and 45% male, then the distributions are homogeneous. n

Example Suppose a teacher teaches two sections of Statistics and uses two different teaching methods. n At the end of the semester, he gives both sections the same final exam and he compares the grade distributions. n He wants to know if the differences that he observes are significant. n

Example Does there appear to be a difference? n Or are the two sets (plausibly) homogeneous? n Method II A 5 7 B 7 11 C 36 18 D 17 7 F 7 5

The Test of Homogeneity The null hypothesis is that the populations are homogeneous. n The alternative hypothesis is that the populations are not homogeneous. H 0: The populations are homogeneous. H 1: The populations are not homogeneous. n Notice that H 0 does not specify a distribution; it just says that whatever the distribution is, it is the same in all rows. n

The Test Statistic n The test statistic is the chi-square statistic, computed as n The question now is, how do we compute the expected counts?

Expected Counts Under the assumption of homogeneity (H 0), the rows should exhibit the same proportions. n We can get the best estimate of those proportions by pooling the rows. n That is, add the rows (i. e. , find the column totals), and then compute the column proportions from them. n

Row and Column Proportions Method II A 5 7 B 7 11 C 36 18 D 17 7 F 7 5

Row and Column Proportions Method II Col Total A 5 7 12 B 7 11 18 C 36 18 54 D 17 7 24 F 7 5 12

Row and Column Proportions Method II Col Total A B C 5 7 36 7 11 18 12 18 54 10% 15% 45% D 17 7 24 20% F 7 5 12 10%

Expected Counts Similarly, the columns should exhibit the same proportions, so we can get the best estimate by pooling the columns. n That is, add the columns (i. e. , find the row totals), and then compute the row proportions from them. n

Row and Column Proportions Method II Col Total A B C 5 7 36 7 11 18 12 18 54 10% 15% 45% D 17 7 24 20% F 7 5 12 10%

Row and Column Proportions Method II Col Total A B C 5 7 36 7 11 18 12 18 54 10% 15% 45% D 17 7 24 20% Row Total F 7 72 5 48 12 10%

Row and Column Proportions Method II Col Total A B C 5 7 36 7 11 18 12 18 54 10% 15% 45% D 17 7 24 20% Row Total F 7 72 60% 5 48 40% 12 10%

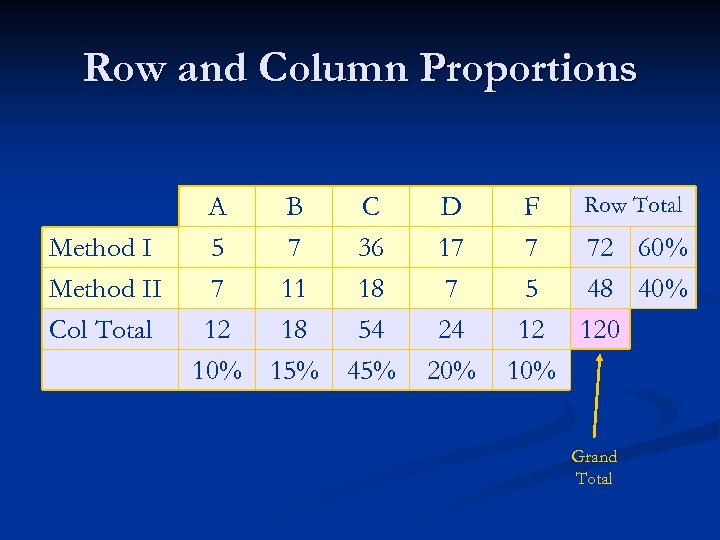Row and Column Proportions Method II Col Total A B C 5 7 36 7 11 18 12 18 54 10% 15% 45% D 17 7 24 20% Row Total F 7 72 60% 5 48 40% 12 120 10% Grand Total

Expected Counts Now apply the appropriate row and column proportions to each cell to get the expected count. n Let’s use the upper-left cell as an example. n According to the row and column proportions, it should contain 60% of 10% of the grand total of 120. n That is, the expected count is 0. 60 0. 10 120 = 7. 2 n

Expected Counts n Notice that this can be obtained more quickly by the following formula. n In the upper-left cell, this formula produces (72 12)/120 = 7. 2

Expected Counts n Apply that formula to each cell to find the expected counts and add them to the table. Method II A 5 (7. 2) 7 (4. 8) B 7 (10. 8) 11 (7. 2) C 36 (32. 4) 18 (21. 6) D 17 (14. 4) 7 (9. 6) F 7 (7. 2) 5 (4. 8)

The Test Statistic n Now compute 2 in the usual way.

Degrees of Freedom n The number of degrees of freedom is df = (no. of rows – 1) (no. of cols – 1). In our example, df = (2 – 1) (5 – 1) = 4. n To find the p-value, calculate 2 cdf(7. 2106, E 99, 4) = 0. 1252. n At the 5% level of significance, the differences are not statistically significant. n

TI-83 – Test of Homogeneity The tables in these examples are not lists, so we can’t use the lists in the TI-83. n Instead, the tables are matrices. n The TI-83 can handle matrices. n

TI-83 – Test of Homogeneity n Enter the observed counts into a matrix. Press MATRIX. n Select EDIT. n Use the arrow keys to select the matrix to edit, say [A]. n Press ENTER to edit that matrix. n Enter the number of rows and columns. (Press ENTER to advance. ) n Enter the observed counts in the cells. n Press 2 nd Quit to exit the matrix editor. n

TI-83 – Test of Homogeneity n Perform the test of homogeneity. Select STATS > TESTS > 2 -Test… n Press ENTER. n Enter the name of the matrix of observed counts. n Enter the name (e. g. , [E]) of a matrix for the expected counts. These will be computed for you by the TI-83. n Select Calculate. n Press ENTER. n

TI-83 – Test of Homogeneity n The window displays The title “ 2 -Test”. n The value of 2. n The p-value. n The number of degrees of freedom. n n See the matrix of expected counts. Press MATRIX. n Select matrix [E]. n Press ENTER. n

Example Is the color distribution in Skittles candy the same as in M & M candy? n One package of Skittles: n Red: 12 n Orange: 14 n Yellow: 10 n Green: 10 n Purple: 12 n

Example n One package of M & Ms: Red: 8 n Orange: 19 n Yellow: 4 n Green: 8 n Blue: 10 n Brown: 6 n

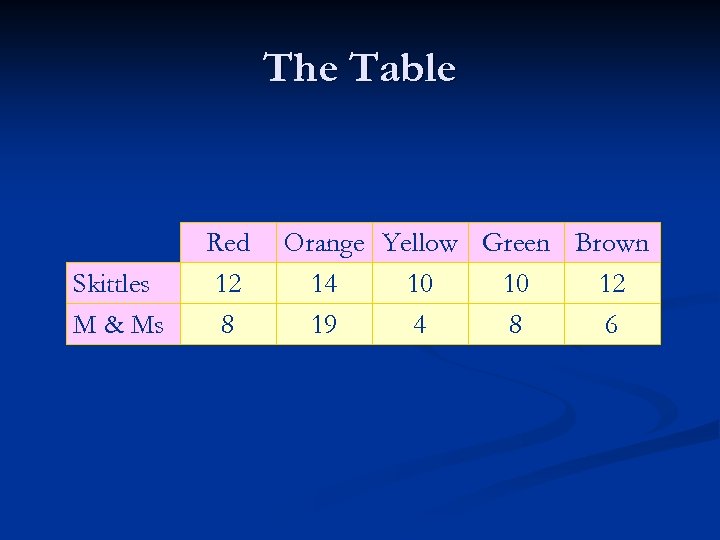The Table Skittles M & Ms Red 12 8 Orange Yellow Green Brown 14 10 10 12 19 4 8 6

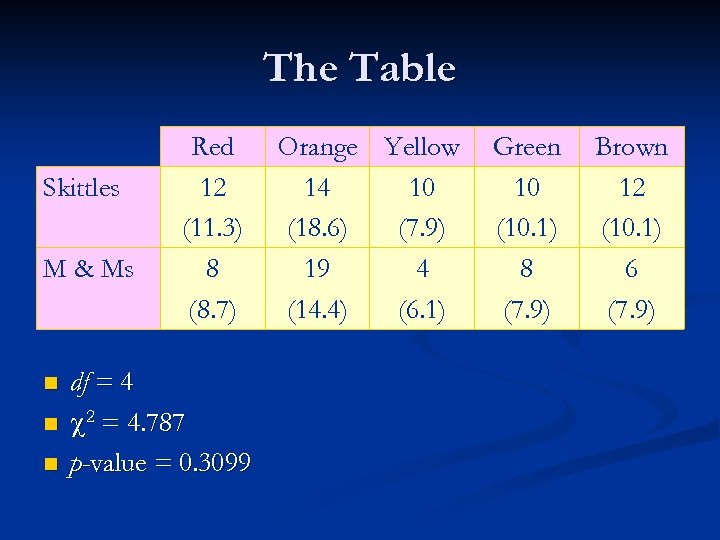The Table Skittles M & Ms n n n Red 12 (11. 3) 8 (8. 7) df = 4 2 = 4. 787 p-value = 0. 3099 Orange Yellow 14 10 (18. 6) (7. 9) 19 4 (14. 4) (6. 1) Green 10 (10. 1) 8 (7. 9) Brown 12 (10. 1) 6 (7. 9)

Example Let’s gather more evidence. Buy a second package of Skittles and add it to the first package. n Second package of Skittles: n Red: 10 n Orange: 13 n Yellow: 15 n Green: 13 n Purple: 7 n

Example Buy a second package of M & Ms and add it to the first package. n Second package of M & Ms: n Red: 5 n Orange: 12 n Yellow: 16 n Green: 9 n Blue: 8 n Brown: 8 n

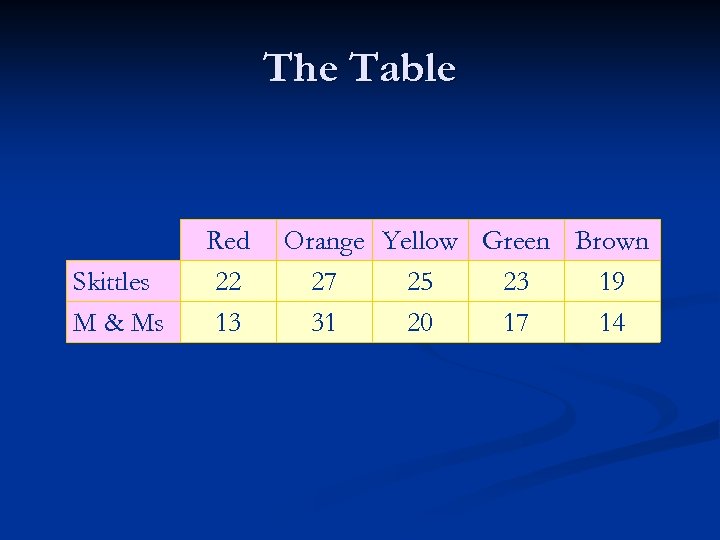The Table Skittles M & Ms Red 22 13 Orange Yellow Green Brown 27 25 23 19 31 20 17 14

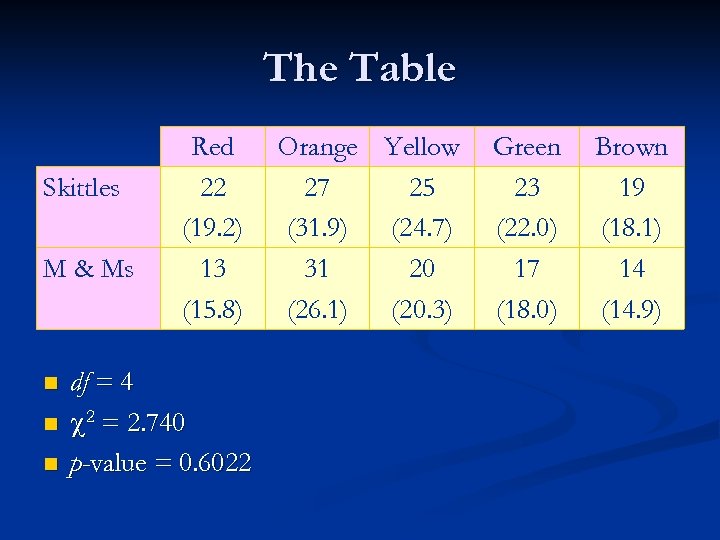The Table Skittles M & Ms n n n Red 22 (19. 2) 13 (15. 8) df = 4 2 = 2. 740 p-value = 0. 6022 Orange Yellow 27 25 (31. 9) (24. 7) 31 20 (26. 1) (20. 3) Green 23 (22. 0) 17 (18. 0) Brown 19 (18. 1) 14 (14. 9)