Terrestrial Data Structures Representing the Earth From the

Terrestrial Data Structures Representing the Earth: From the 3 D Globe to the 2 D map 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 1

Course Content Part I: Overview • Fundamentals of GIS • Hands-on Intro to Arc. GIS – (lab sessions @ 4: 00 -7: 00 pm or 7: 00 -10: 00 pm) Part II: Principles • Terrestrial data structures – representing the real world • GIS Data Structures Part III: Practice • Data Input: preparation and integration • Data analysis and modeling • Data output and application examples Part IV: The Future • Future of GIS – representing the world in a computer • Data Quality – An essential ingredient 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 2

Terrestrial Data Structures Pop Quiz or Cocktail Conversation • name the states containing the most northerly, easterly, westerly and southerly points of the US. • land area of Canada is about: (a) twice (b) same ( c) half that of US? • a degree of latitude is (a) slightly longer (b) same ( c) slightly shorter at the poles than at the equator ? Some Light Reading – Sobel, Dava Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time London: Fourth Estate, 1996 (paperback 1998) – Linklater, Arlo Measuring America Peguin Books, 2002 (a fascinating history of surveying, the Public Land Survey System, measurement and its standardization) Some Light Viewing (movie) – The Englishman Who Went Up a Hill and Came Down a Mountain 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 3

…the most southerly point in the US Where am I? 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 4

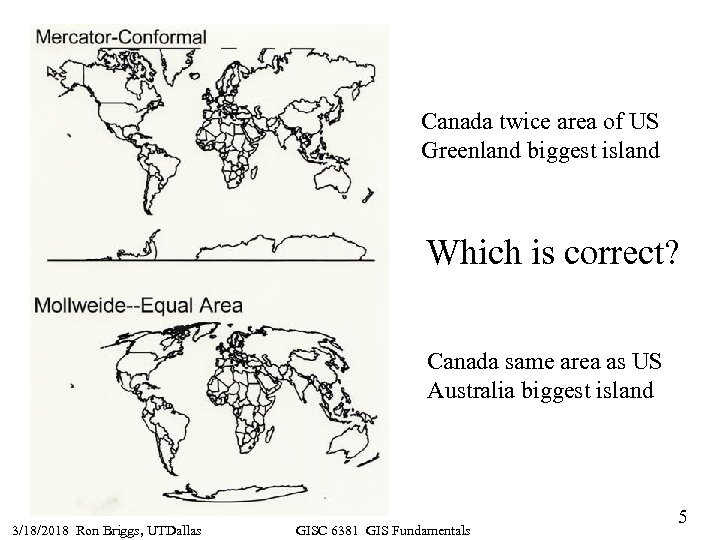Canada twice area of US Greenland biggest island Which is correct? Canada same area as US Australia biggest island 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 5

Representing the Earth: Topics • • • Geoid and Spheroids: modeling the earth Latitude and Longitude: position on the model Datums and Surveying: measuring the model Map Projections: converting the model to 2 dimensions Scale: sizing the model – cover under Data Quality 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 6

The Shape of the Earth • topographic surface 3 concepts – the land/air interface – complex (rivers, valleys, etc) and difficult to model • geoid – a continuous surface which is perpendicular at every point to the direction of gravity ---surface to which a plumb line is perpendicular – approximates mean sea-level in open ocean without tides, waves or swell – “that surface to which the oceans would conform over the entire earth if free to adjust to the combined effect of the earth's mass attraction and the centrifugal force of the earth's rotation. ” Burkhard 1959/84 – satellite observation (after 1957) showed it to be somewhat irregular ‘cos of local variations in gravity resulting from the uneven distribution of the earth’s mass. • Spheres and spheroids (3 -dimensional circle and ellipse) – mathematical models used to approximate the geoid and provide the basis for accurate location (horizontal) and elevation (vertical) measurement – sphere (3 -dimensional circle) with radius of 6, 370, 997 m considered ‘close enough’ for small scale maps (1: 5, 000 and below - e. g. 1: 7, 500, 000) – spheroid (3 -dimensional ellipse, flattened at the poles) should be used for larger scale maps of 1: 1, 000 or more (e. g. 1: 24, 000) – the issue is, which spheroid?

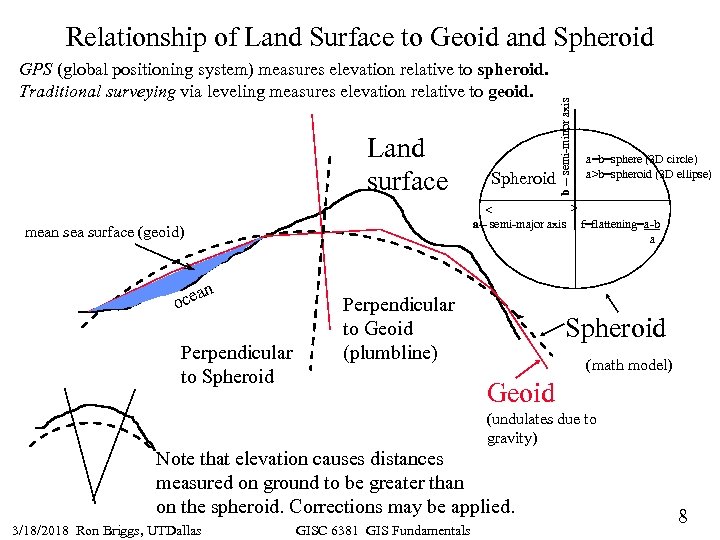GPS (global positioning system) measures elevation relative to spheroid. Traditional surveying via leveling measures elevation relative to geoid. Land surface Spheroid b -- semi-minor axis Relationship of Land Surface to Geoid and Spheroid a=b=sphere (3 D circle) a>b=spheroid (3 D ellipse) > < a-- semi-major axis f=flattening=a-b a mean sea surface (geoid) n a oce Perpendicular to Spheroid Perpendicular to Geoid (plumbline) Spheroid (math model) Geoid (undulates due to gravity) Note that elevation causes distances measured on ground to be greater than on the spheroid. Corrections may be applied. 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 8

Which Spheroid? Hundreds have been defined depending upon: Most commonly encountered are: • – available measurement technology – area of the globe (e. g North America, • Africa) – map extent (country, continent or global) • – political issues (e. g Warsaw pact versus NATO) • ARC/INFO supports 26 different spheroids! – conversions via math. formulae Earth measurements (approx. ): equatorial radius: 6, 378 km 3, 963 mi polar radius: 6, 357 km 3, 950 mi (flattened about 13 miles at poles) 3/18/2018 Ron Briggs, UTDallas • Everest (Sir George) 1830 – one of the earliest spheroids; India – a=6, 377, 276 m b=6, 356, 075 m f=1/300. 8 Clarke 1886 for North America – basis for USGS 7. 5 Quads – a=6, 378, 206. 4 m b=6, 356, 583. 8 m f=1/295 GRS 80 (Geodetic Ref. System, 1980) – current North America mapping – a=6, 378, 137 m b=6, 356, 752. 31414 m f=1/298 Hayford or International (1909/1924) – early global choice – a=6, 378, 388 b=6, 356, 911. 9 m f= • WGS 84 (World Geodetic Survey, 1984) – current global choice – a=6, 378, 137 b=6, 356, 752. 31 m f= GISC 6381 GIS Fundamentals 9

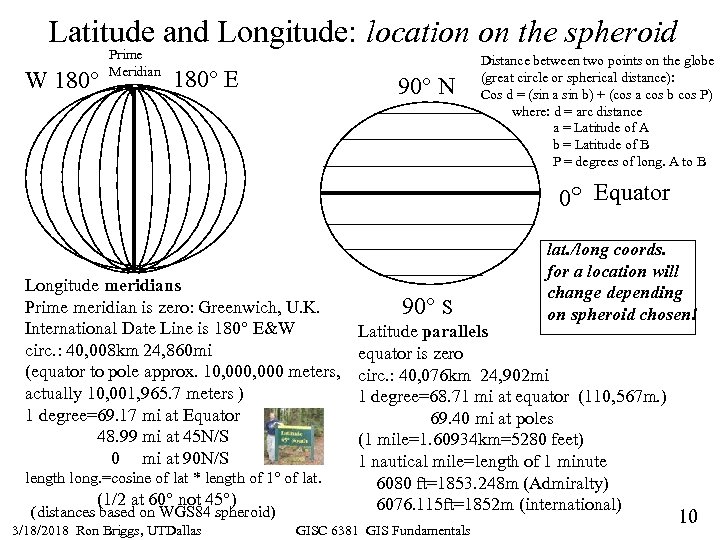Latitude and Longitude: location on the spheroid W 180° Prime Meridian 180° E 90° N Distance between two points on the globe (great circle or spherical distance): Cos d = (sin a sin b) + (cos a cos b cos P) where: d = arc distance a = Latitude of A b = Latitude of B P = degrees of long. A to B 0° Equator Longitude meridians Prime meridian is zero: Greenwich, U. K. International Date Line is 180° E&W circ. : 40, 008 km 24, 860 mi (equator to pole approx. 10, 000 meters, actually 10, 001, 965. 7 meters ) 1 degree=69. 17 mi at Equator 48. 99 mi at 45 N/S 0 mi at 90 N/S length long. =cosine of lat * length of 1° of lat. (1/2 at 60° not 45°) (distances based on WGS 84 spheroid) 3/18/2018 Ron Briggs, UTDallas 90° S lat. /long coords. for a location will change depending on spheroid chosen! Latitude parallels equator is zero circ. : 40, 076 km 24, 902 mi 1 degree=68. 71 mi at equator (110, 567 m. ) 69. 40 mi at poles (1 mile=1. 60934 km=5280 feet) 1 nautical mile=length of 1 minute 6080 ft=1853. 248 m (Admiralty) 6076. 115 ft=1852 m (international) GISC 6381 GIS Fundamentals 10

Latitude and Longitude Graticule Prime Meridian NW + - NE + + SW - - SE - + When entering data, be sure to include negative signs. Longitude sometimes recorded using 360° to avoid negatives. Lat and long measured in: degrees° minutes” seconds’ (60’=1” & 60”=1°) UTD: 32° 59” 16. 0798 N 96° 44” 56. 9522 W 1 second=100 ft or 30 m. approx. (lat. , or long. at equator) Decimal degrees, not minutes/seconds, best for GIS. dd= d° + m”/60 + s’/3600 Carry enough decimal points for accuracy! 6 decimals give 4 inch (10 cm) accuracy (but must use double precision storage-single precision accurate to only 2 m) UTD: 32. 98779994 N 96. 74915339 W (8 decimals-->1 millimeter accuracy!) (note: 1 meter= 3. 2808 feet) graticule: network of lines on globe or map representing latitude and longitude. Origin is at Equator/Prime Meridian intersection (0, 0) grid: set of uniformly spaced straight lines intersecting at right angles. (XY Cartesian coordinate system) Latitude normally listed first (lat, long), the reverse of the convention for X, Y Cartesian coordinates 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 11

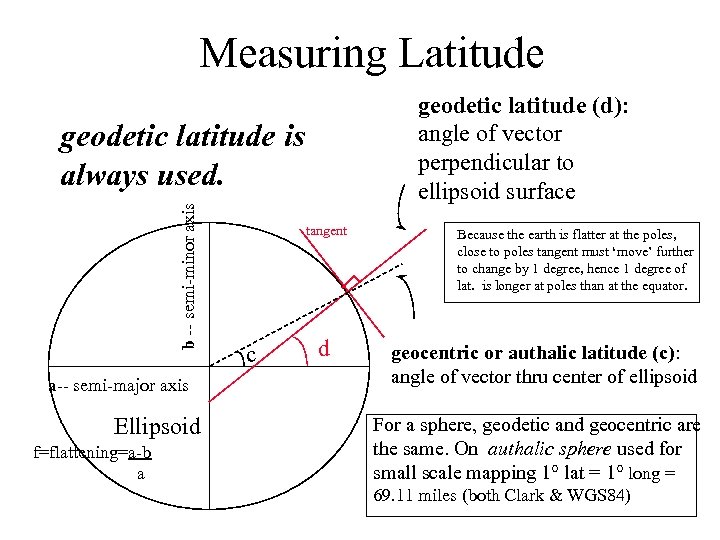Measuring Latitude geodetic latitude (d): angle of vector perpendicular to ellipsoid surface b -- semi-minor axis geodetic latitude is always used. a-- semi-major axis Ellipsoid f=flattening=a-b a tangent c d Because the earth is flatter at the poles, close to poles tangent must ‘move’ further to change by 1 degree, hence 1 degree of lat. is longer at poles than at the equator. geocentric or authalic latitude (c): angle of vector thru center of ellipsoid For a sphere, geodetic and geocentric are the same. On authalic sphere used for small scale mapping 1° lat = 1° long = 69. 11 miles (both Clark & WGS 84)

N 0° S E W Bisected by a hemisphere! 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 13

Geodesy & Surveying Process of measuring position (horizontal control) and elevation (vertical control) of points on earth’s surface (spheroid) • Geodetic Surveying: incorporates earth’s shape and curvature – – • used to establish location of survey monuments which provide basis for all measurements. conducted in US by the National Geodetic Service (previously the US Coast and Geodetic Survey) in the Dept. of Commerce. Plane Surveying: assumes earth is flat – employed by local surveyors for small geographic area (building site, sub-division, etc. ) – usually uses survey monuments as starting point. Techniques: – all employ ‘triangulation: ’ using geometry to impute unknown positions and distances based on certain measured angles or distances between other known locations. – earlier techniques based on visual sighting (from starting point, then back to it) using: • invar-tape (very small coefficient of expansion) for distance measurement • theodolites (or less accurate transits in local surveys) to measure angles for horizontal positioning (also measure vertical angles for elevation) • levels and graduated rods for accurate vertical measurement. – modern techniques use: • laser based instruments to measure distances • gps (global positioning system) receivers to establish location and elevation • cost one fifth as much as traditional approaches! 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 14

Datums: --any numerical or geometrical quantity or set of such quantities which serve as a reference or base for other quantities --all horizontal or vertical positions are relative to a specific datum For the Geodesist (and for GIS) • a set of parameters defining a coordinate system, including: – the spheroid (earth model) – a point of origin and an orientation relative to earth’s axis of rotation (ties spheroid to earth) For the Local Surveyor • a set of points whose precise location and /or elevation has been determined, which serve as reference points from which other locations can be determined (horizontal datum) • a surface to which elevations are referenced usually ‘mean sea level’ (vertical datum) • points usually marked with brass plates called survey markers or monuments whose identification codes and precise locations (usually in lat/long) are published. Unlike with spheroids and map projections, there is not necessarily a math. formulae for conversion between datums, although ‘equivalency tables’ may be available 15 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals

• Original North American Datums NAD 83 1900 US Standard Datum – first nationwide datum – Clark 1866 spheroid – origin Meades Ranch, Osborne Cnty, KS (39 -13 -26. 686 N 98 -32 -30. 506 W) – determined by visual triangulation – approx. 2, 500 points – renamed North American Datum (NAD) in 1913 when adopted by Mexico and Canada • NAD 27 – – – Clark 1866 spheroid Meades Ranch origin visual triangulation 25, 000 stations (250, 000 by 1970) NAVD 29 (North American Vertical Datum, 1929) provided elevation – basis for most USGS 7. 5 minute quads 3/18/2018 Ron Briggs, UTDallas – satellite (since 1957) and laser distance data showed inaccuracy of NAD 27 – 1971 National Academy of Sciences report recommended new datum – used GRS 80 spheroid (functionally equivalent to WGS 84 altho. not identical) – origin: Mass-center of Earth – 275, 000 stations – “Helmert blocking” least squares technique fitted 2. 5 million other fed, state and local agency points. – NAVD 88 provides vertical datum – points can differ up to 160 m from NAD 27, but seldom more than 30 m, (and data from a digitized map more inaccurate than datum difference) – no mathematical formulae for conversion from NAD 27: See USGS Survey Bulletin # 1875 for conversion tables (in ARC/INFO) – completed in 1986 therefore called NAD 83 (1986)! – but new data coming from gps was more accurate! GISC 6381 GIS Fundamentals 16

Current US Datum Programs: National Geodetic Reference System(NGRS)/ National Spatial Reference System(NSRS) Continuously Operating Reference Stations (CORS) ( first called HPGN-High Precision GPS Network) – NAD 83 not ‘gps-able’ • continuos measurement of location • inaccessible monuments (hill tops) from GPS satellites • irregular spacing of monuments • 500 km spacing – get destroyed • DFW site in Arlington run by – too many (275, 000) to maintain TXDOT (about 70 in TX as of 2007) • insufficient accuracy for precision work (at 1 m or less) – 3 -Tier Plan • posted hourly on the Internet • federal base network (FBN) • Use for differential GPS, calibrating – ~1, 600 -2, 000 monuments gps instruments, monitor crustal – 5 -8 mm accuracy (A or B order) movement, etc. – evenly spaced 1 degree by 1 degree (75 -125 kms); – 3 year visitation cycle • datum revision know as NAD 83 • cooperative base network (CBN-states) (CORSxx) since several been – ~16, 000 monuments released (‘ 93, ‘ 94, ’ 96, etc) – 25 -30 km spacing; B-order accuracy High Accuracy Reference Network (HARN) – no coop agreement with Texas! • user densification network – Diff. from NAD 83 (HARN) <10 cm Reference – local points connected to FBN/CBN Lapine, Lewis A. National Geodetic Survey: Its Mission, Vision, and Goals, US Dept of – Revision known as NAD 83(HARN) Commerce, NOAA, October, 1994 • Issued on a regional basis from 1989 thru 1997 Snay and Soler Professional Surveyor Dec 1999, • Differs from NAD 83 (1986) by <=1 m (horizon. ) Feb 2000 17 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals

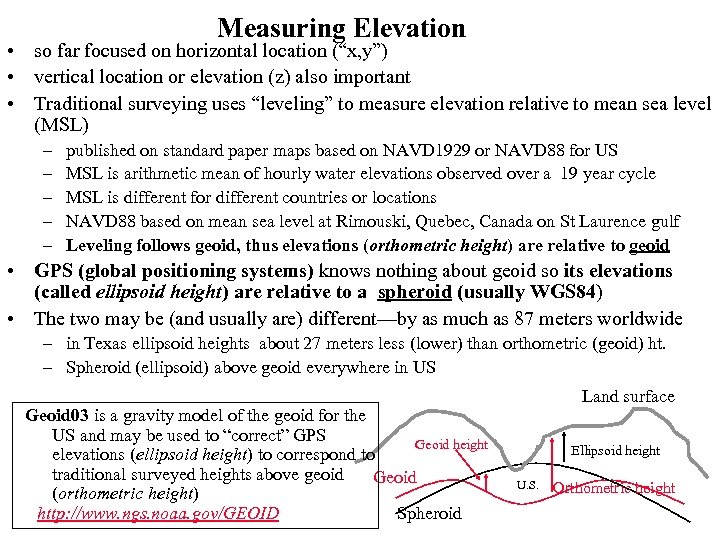Measuring Elevation • so far focused on horizontal location (“x, y”) • vertical location or elevation (z) also important • Traditional surveying uses “leveling” to measure elevation relative to mean sea level (MSL) – – – published on standard paper maps based on NAVD 1929 or NAVD 88 for US MSL is arithmetic mean of hourly water elevations observed over a 19 year cycle MSL is different for different countries or locations NAVD 88 based on mean sea level at Rimouski, Quebec, Canada on St Laurence gulf Leveling follows geoid, thus elevations (orthometric height) are relative to geoid • GPS (global positioning systems) knows nothing about geoid so its elevations (called ellipsoid height) are relative to a spheroid (usually WGS 84) • The two may be (and usually are) different—by as much as 87 meters worldwide – in Texas ellipsoid heights about 27 meters less (lower) than orthometric (geoid) ht. – Spheroid (ellipsoid) above geoid everywhere in US Geoid 03 is a gravity model of the geoid for the US and may be used to “correct” GPS Geoid height elevations (ellipsoid height) to correspond to traditional surveyed heights above geoid Geoid (orthometric height) http: //www. ngs. noaa. gov/GEOID Spheroid Land surface Ellipsoid height U. S. Orthometric height

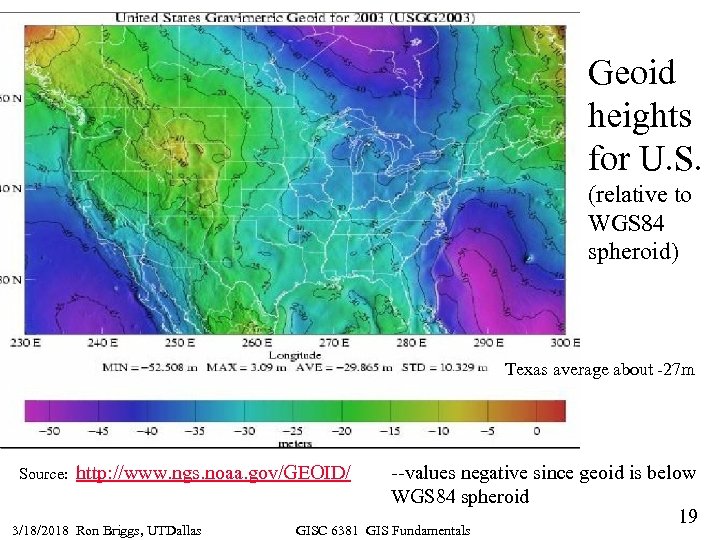Geoid heights for U. S. (relative to WGS 84 spheroid) Texas average about -27 m Source: http: //www. ngs. noaa. gov/GEOID/ 3/18/2018 Ron Briggs, UTDallas --values negative since geoid is below WGS 84 spheroid 19 GISC 6381 GIS Fundamentals

Measuring Area (reference) Acre is the standard measurement of land area in the US • Originally, the area that could be worked by a team of oxen in a day (approximately!), and varied from state to state in Ben Franklin’s days! • Equals 43, 560 sq. feet, 4, 840 sq. yards, or 10 sq. chains • A surveyor’s chain (or Gunter’s Chain) is 66 feet long – A rod, pole or perch is 16. 5 feet, thus 4 rods equals a chain • An acre is 1 chain by 10 chains, or 66 feet by 660 feet • 640 acres in a square mile Hectare • Standard measurement of land area in metric system • Equals 100 meters by 100 meters, or 10, 000 square meters – 100 hectares in a square kilometer • Equivalent to 2. 471 acres or 107, 639 square feet. For fascinating detail, see A. Linklater, Measuring America Peguin Books, 2002 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 20

Map Projections: the concept • A method by which the curved 3 D surface of the earth is represented on a flat 2 D map surface. • a two dimensional representation, using a plane coordinate system, of the earth’s three dimensional sphere/spheroid • location on the 3 D earth is measured by latitude mad longitude; • location on the 2 D map is measured by x, y Cartesian coordinates • unlike choice of spheroid, choice of map projection does not change a location’s lat/long coords, only its XY coords. 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 21

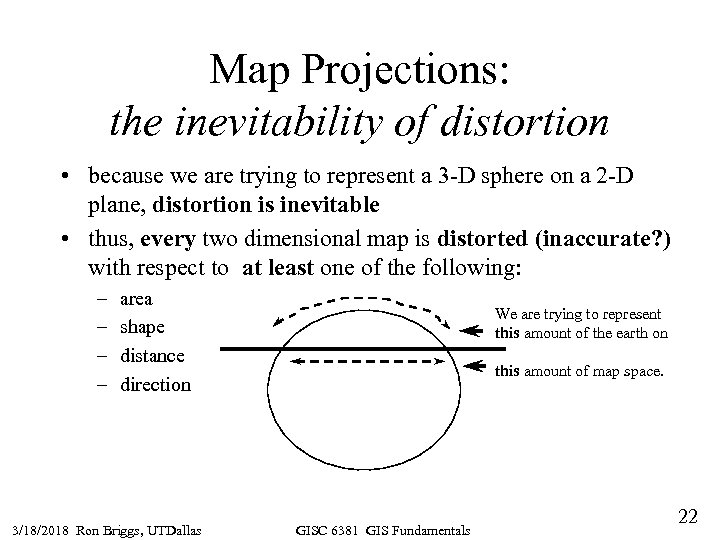Map Projections: the inevitability of distortion • because we are trying to represent a 3 -D sphere on a 2 -D plane, distortion is inevitable • thus, every two dimensional map is distorted (inaccurate? ) with respect to at least one of the following: – – area shape distance direction 3/18/2018 Ron Briggs, UTDallas We are trying to represent this amount of the earth on this amount of map space. GISC 6381 GIS Fundamentals 22

Map Projections: classification Classified by property preserved or by geometrical model Property Preserved Geometric Model Used • • Equal area projections preserve the area of features (popular in GIS) Conformal projections preserve the shape of small features (good for presentations) , and show local directions (bearings) correctly (useful for coastal navigation!) Equidistant projections preserve distances (scale) to places from one point, or along a one or more lines True direction projections preserve bearings (azimuths) either locally (in which case they are also conformal) or from center of map. Azimuth: angle between a great circle (line on globe) and a meridian. 3/18/2018 Ron Briggs, UTDallas – – along one line (tangent) or cuts thru globe along two lines (secant) (usually parallels of latitude) cone is then unfolded to create “flat map” • – Scale can never be correct everywhere on any map • • Planar/Azimuthal/Zenithal: image of spherical globe is projected onto a map plane which is tangent to (touches) globe at single point conical: image of spherical globe is projected onto a cone which touches cylindrical: image of spherical globe is projected onto a cylinder which again – may be tangent along one line, – or secant along two lines – again, cylinder is unfolded to create a “flat map” See Apppendix for detail GISC 6381 GIS Fundamentals 23

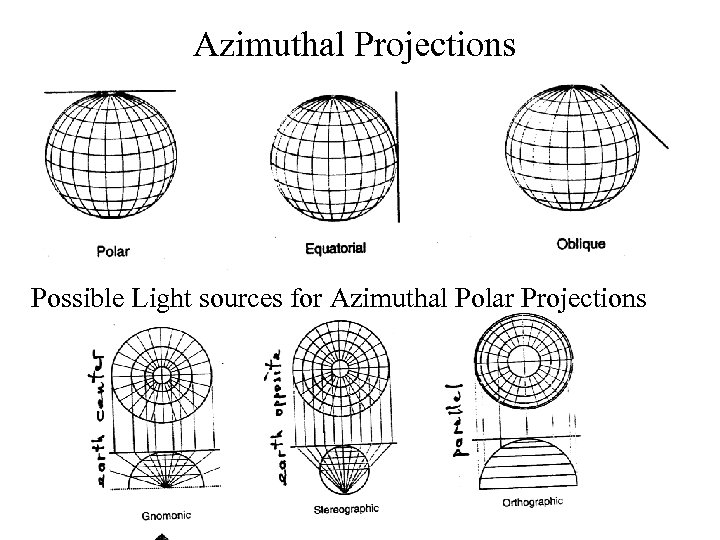Azimuthal Projections Possible Light sources for Azimuthal Polar Projections

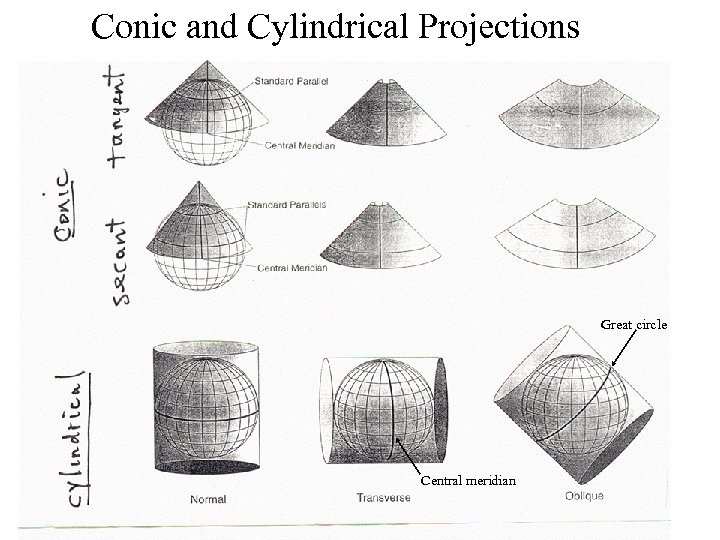Conic and Cylindrical Projections Great circle Central meridian

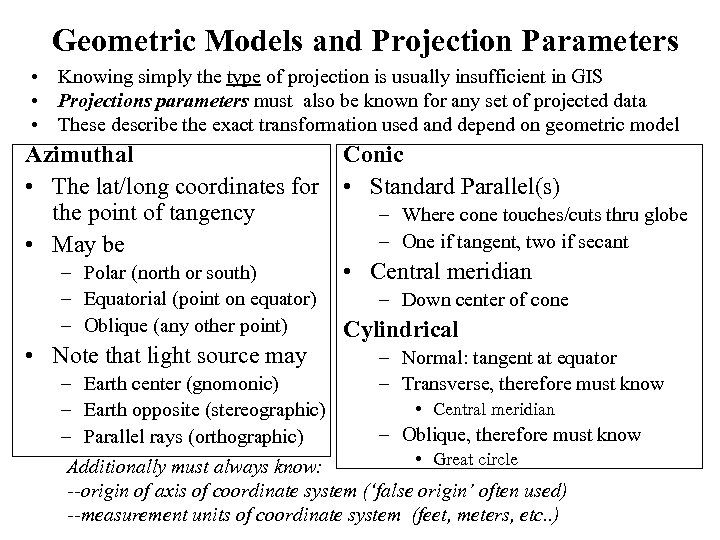Geometric Models and Projection Parameters • Knowing simply the type of projection is usually insufficient in GIS • Projections parameters must also be known for any set of projected data • These describe the exact transformation used and depend on geometric model Azimuthal • The lat/long coordinates for the point of tangency • May be – Polar (north or south) – Equatorial (point on equator) – Oblique (any other point) • Note that light source may Conic • Standard Parallel(s) – Where cone touches/cuts thru globe – One if tangent, two if secant • Central meridian – Down center of cone Cylindrical – Normal: tangent at equator – Transverse, therefore must know – Earth center (gnomonic) • Central meridian – Earth opposite (stereographic) – Oblique, therefore must know – Parallel rays (orthographic) • Great circle Additionally must always know: --origin of axis of coordinate system (‘false origin’ often used) --measurement units of coordinate system (feet, meters, etc. . )

Commonly Encountered Map Projections in GIS • American Polyconic – early projection used by USGS; usually only encountered on older maps; replaced by transverse mercator. – “Neither conformal nor equivalent, it minimizes distance distortion on large scale maps” (quote from Monmonier: http: //www. markmonmonier. com/work 6. htm) • Albers Conic Equal-Area – often used for US base maps showing all of the “lower 48” states – standard parallels set at 29 1/2 N and 45 1/2 N • Lambert Conformal Conic – often used for US Base map of all 50 states (including Alaska and Hawaii), with standard parallels set at 37 N and 65 N – also for State Base Map series, with standard parallels at 33 N and 45 N – also used in State Plane Coordinate System (SPCS) – Great circles (shortest distance point to point on globe) are straight lines • Transverse Mercator (conformal cylindrical) – used in SPCS for States with major N/S extent – Basis for Universal Transverse Mercator (UTM) systems used for standardized mapping worldwide and for United States National Grid (USNG) Most commonly, for relatively large scale maps, you encounter the last 3 projections, along with the SPCS and UTM projections systems which use them. 27 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals

Universal Transverse Mercator (UTM) • • • first adopted by US Army in 1947 for large scale maps worldwide used from lat. 84°N to 80°S; Universal Polar Stereographic (UPS) used for polar areas globe divided into 60 N/S zones, each 6° wide; these are numbered from one to sixty going east from 180 th meridian – Conformal, and by using transverse form with zones, area distortion significantly reduced • each zone divided into 20 E/W bands (or “belts”), each 8° high lettered from the south pole using C thru X (O and I omitted) thus north Texas in “S” belt from 32° (thru Hillsboro) to 40° (Nebraska/Kansas line). – These belts of no real relevance for UTM, but important for MGRS and USNG (next slide) • the meridian halfway between the two boundary meridians for each zone is designated as the central meridian and a secant cylindrical projection is done for each zone – Central meridian for zone 1 is at 177° W – Standard meridians (secant projection) are approx. 150 km either side of this; scale correct here • • scale of central meridian reduced by. 9996 to minimize scale variation in zone resulting in accuracy variation of approx. 1 meter per 2, 500 meters coordinate origins are set: – For Y: at equator for northern hemisphere; at 10, 000 m S. of equator for southern hemi. – For X: at 500, 000 m west of central meridian – thus no negative values within zone, and central meridian is at 500, 000 m East 40 N KS/NE line 102 W 96 W UTM in Texas: 14 13 Midland 3 zones 15 Lake Tawakoni Dallas is in 14 S Definitive documentation: http: //earth-info. nga. mil/Gand. G/publications/tm 8358. 2/TM 8358_2. pdf 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals Band “S” 32 N Hillsboro 28

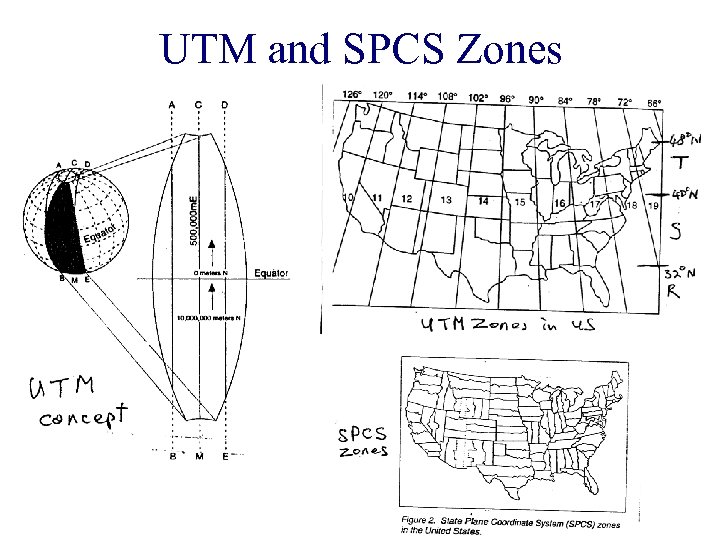UTM and SPCS Zones

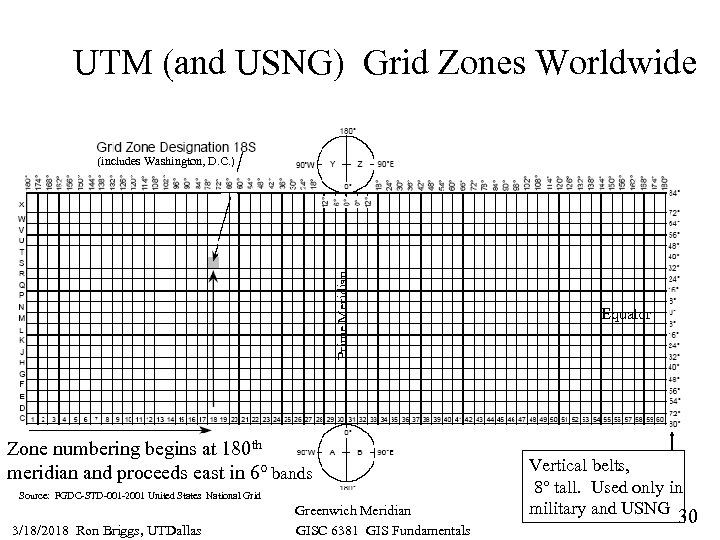UTM (and USNG) Grid Zones Worldwide Prime Meridian (includes Washington, D. C. ) Zone numbering begins at 180 th meridian and proceeds east in 6° bands Source: FGDC-STD-001 -2001 United States National Grid 3/18/2018 Ron Briggs, UTDallas Greenwich Meridian GISC 6381 GIS Fundamentals Equator Vertical belts, 8° tall. Used only in military and USNG 30

Prime Meridian Equator UTM (and USNG) Grid Zones Worldwide Superimposed on world map 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals Source: Wikipedia 31

Military Grid Reference System (MGRS & United States National Grid (USNG) • MGRS developed initially by US military and then adopted by the FGDC (Federal Geographic Data Committee) as the USNG formal standard in 2001 (FGDC-STD-011 -2001) – • Goals is to provide standard coordinate based “address locator” applicable to both analog and digital maps, supporting – – • Consequently MGRS and USNG are the same within the US Disaster response Location based services (where is closest Mac. Donalds? ) Based on UTM. – Each primary UTM Grid Zone Designation (GZD) (the 6 ° long. by 8 ° lat. areas) identified by a number/letter combination (e. g 14 S for north Texas, 18 S for central east coast of US) – Each GZD divided into 100, 000 meter by 1000, 000 meter (100 km x 100 km) squares each identified by two letters (QB for DFW, UJ for Washington, D. C. ) – Within each 100, 000 -meter-square, points locations are based on UTM east/north coordinates • Easting (“read across”) and northing (“then go up”) must always have the same number of digits. • number of digits used depends on precision requirements – Example for Washington monument – – – – 18 S--locates within the 6 ° long. by 8 ° lat. zone 18 SUJ—locates within a 100 km by 100 km square 18 SUJ 20 --Locates with a precision of 10 km (within a 10 km square) 18 SUJ 2306 - Locates with a precision of 1 km (uses 2 digits) 18 SUJ 234064 – Locates with a precision of 100 meters (3 digits—within a city block) 18 SUJ 23480647 - Locates with a precision of 10 meters (4 digits—a single house) 18 SUJ 2348306479 - Locates with a precision of 1 meter (5 digits—a parked vehicle) – Founders Bldg UTD: 14 S QB 10316 52184 (1 meter precision) for more info: http: //www. fgdc. gov/usng/ http: //usgrid. gmu. edu/resources. html 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 32

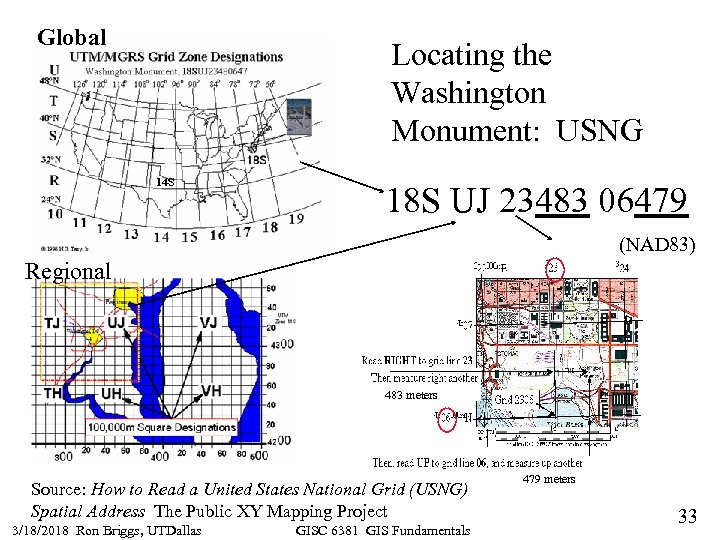Global Locating the Washington Monument: USNG 14 S 18 S UJ 23483 06479 (NAD 83) Regional 483 meters Source: How to Read a United States National Grid (USNG) Spatial Address The Public XY Mapping Project 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 479 meters 33

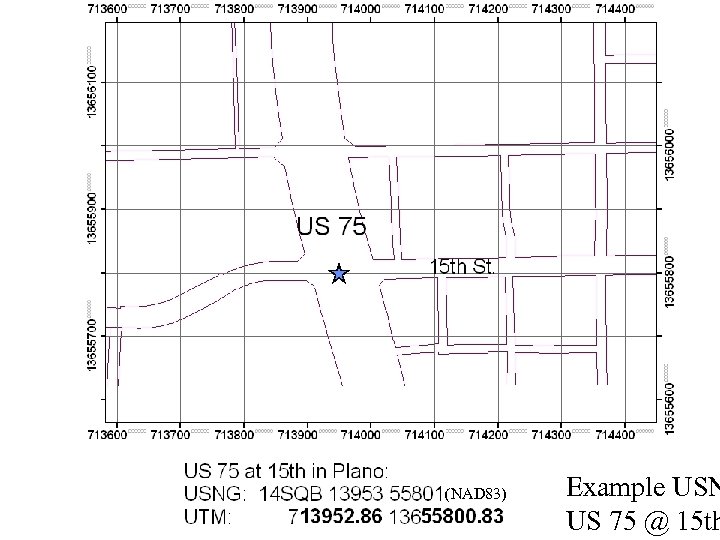(NAD 83) 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals Example USN 34 US 75 @ 15 th

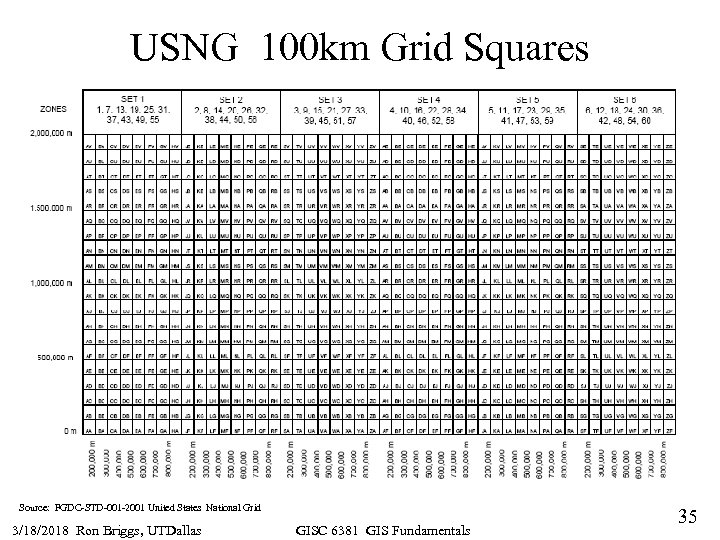USNG 100 km Grid Squares Source: FGDC-STD-001 -2001 United States National Grid 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 35

State Plane Coordinate System (SPCS) • • began in 1930 s for public works projects; popular with interstate designers. states divided into 1 or more zones (~130 total for US) – each zone designed to maintain scale distortion to less than 1 part per 10, 000 • • Texas has 5 zones running E/W: north (5326/4201), north central (5351/4202), Central (5376/4203), south central (5401/4204), south (5426/4205) (datum. ID/fips. ID) Different projections used: – transverse mercator (conformal) for States with large N/S extent – Lambert conformal conic for rest (incl. Texas) – some states use both projections (NY, FL, AK) – oblique mercator used for Alaska panhandle • each zone also has: – unique standard parallels (2 for Lambert) or central meridian (1 for mercator) – false coordinate origins which differ between zones, and use feet for NAD 27 and meters for NAD 83 – (1 m=39. 37 inches exact used for conversion; differs slightly from NBS 1”=2. 54 cm) – scale reduction used to balance scale across entire zone resulting in accuracy variation of approx. 1 per 10, 000 thus 4 times more accurate than UTM • See Snyder, 1982 USGS Bulletin # 1532, p. 56 -63 for details

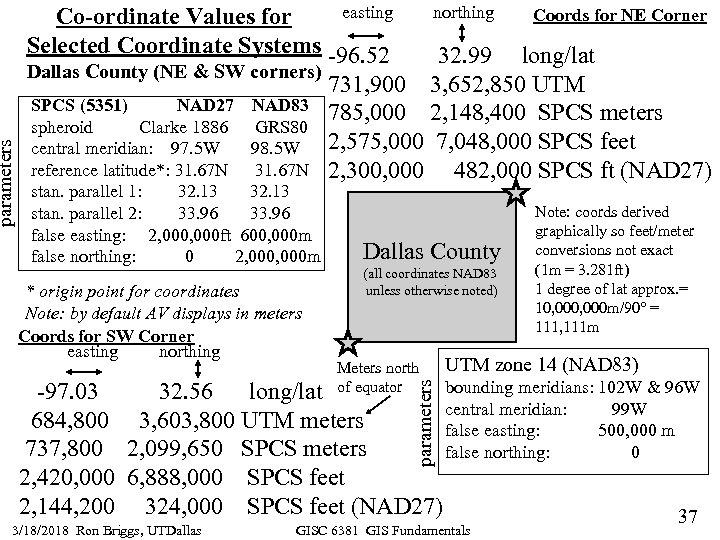parameters easting Co-ordinate Values for Selected Coordinate Systems -96. 52 northing Coords for NE Corner 32. 99 long/lat Dallas County (NE & SW corners) 731, 900 3, 652, 850 UTM SPCS (5351) NAD 27 NAD 83 785, 000 2, 148, 400 SPCS meters spheroid Clarke 1886 GRS 80 2, 575, 000 7, 048, 000 SPCS feet central meridian: 97. 5 W 98. 5 W reference latitude*: 31. 67 N 2, 300, 000 482, 000 SPCS ft (NAD 27) stan. parallel 1: 32. 13 stan. parallel 2: 33. 96 false easting: 2, 000 ft 600, 000 m false northing: 0 2, 000 m * origin point for coordinates Note: by default AV displays in meters Coords for SW Corner easting northing Dallas County (all coordinates NAD 83 unless otherwise noted) Meters north of equator Note: coords derived graphically so feet/meter conversions not exact (1 m = 3. 281 ft) 1 degree of lat approx. = 10, 000 m/90° = 111, 111 m UTM zone 14 (NAD 83) parameters bounding meridians: 102 W & 96 W -97. 03 32. 56 long/lat central meridian: 99 W 684, 800 3, 603, 800 UTM meters false easting: 500, 000 m 737, 800 2, 099, 650 SPCS meters false northing: 0 2, 420, 000 6, 888, 000 SPCS feet 2, 144, 200 324, 000 SPCS feet (NAD 27) 37 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals

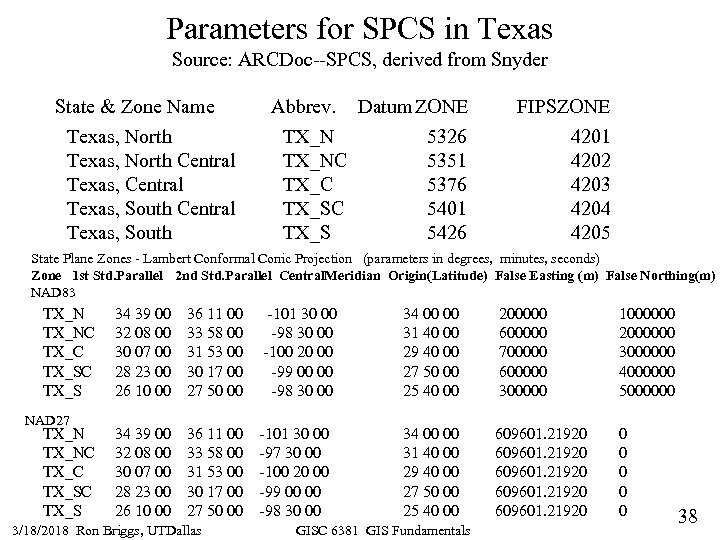Parameters for SPCS in Texas Source: ARCDoc--SPCS, derived from Snyder State & Zone Name Texas, North Central Texas, South Abbrev. Datum ZONE TX_N 5326 TX_NC 5351 TX_C 5376 TX_SC 5401 TX_S 5426 FIPSZONE 4201 4202 4203 4204 4205 State Plane Zones - Lambert Conformal Conic Projection (parameters in degrees, minutes, seconds) Zone 1 st Std. Parallel 2 nd Std. Parallel Central. Meridian Origin(Latitude) False Easting (m) False Northing(m) NAD 83 TX_NC TX_SC TX_S NAD 27 TX_NC TX_SC TX_S 34 39 00 32 08 00 30 07 00 28 23 00 26 10 00 36 11 00 33 58 00 31 53 00 30 17 00 27 50 00 -101 30 00 -98 30 00 -100 20 00 -99 00 00 -98 30 00 34 00 00 31 40 00 29 40 00 27 50 00 25 40 00 200000 600000 700000 600000 300000 1000000 2000000 3000000 4000000 5000000 34 39 00 32 08 00 30 07 00 28 23 00 26 10 00 36 11 00 33 58 00 31 53 00 30 17 00 27 50 00 -101 30 00 -97 30 00 -100 20 00 -99 00 00 -98 30 00 34 00 00 31 40 00 29 40 00 27 50 00 25 40 00 609601. 21920 0 0 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 38

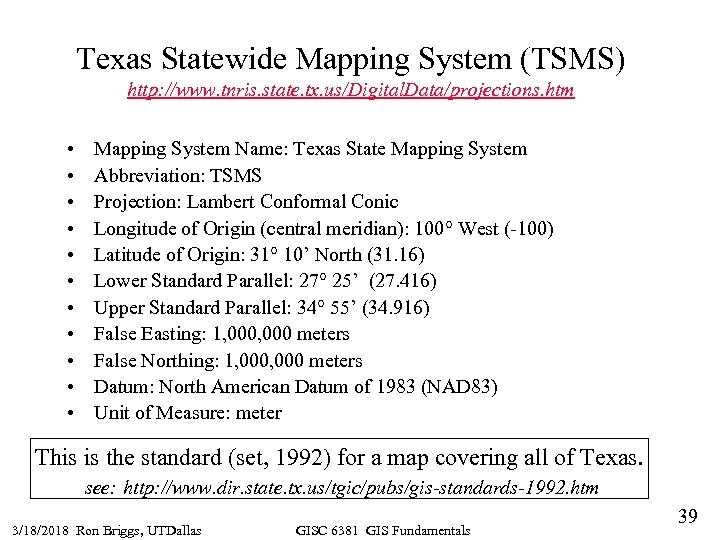Texas Statewide Mapping System (TSMS) http: //www. tnris. state. tx. us/Digital. Data/projections. htm • • • Mapping System Name: Texas State Mapping System Abbreviation: TSMS Projection: Lambert Conformal Conic Longitude of Origin (central meridian): 100° West (-100) Latitude of Origin: 31° 10’ North (31. 16) Lower Standard Parallel: 27° 25’ (27. 416) Upper Standard Parallel: 34° 55’ (34. 916) False Easting: 1, 000 meters False Northing: 1, 000 meters Datum: North American Datum of 1983 (NAD 83) Unit of Measure: meter This is the standard (set, 1992) for a map covering all of Texas. see: http: //www. dir. state. tx. us/tgic/pubs/gis-standards-1992. htm 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 39

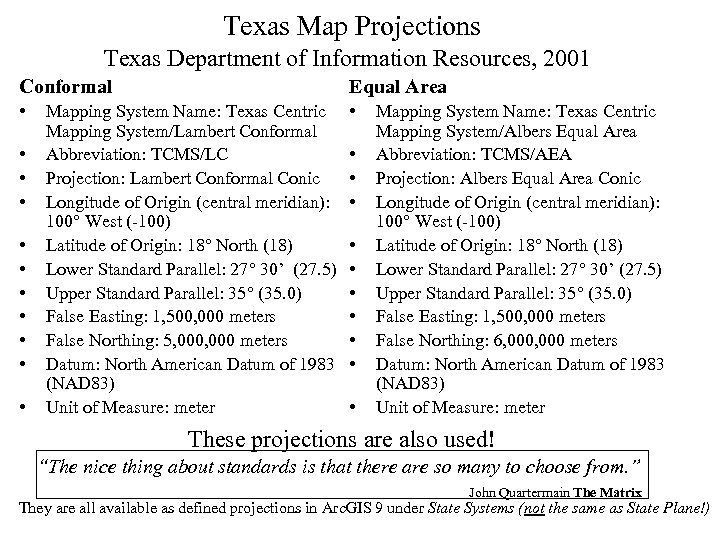Texas Map Projections Texas Department of Information Resources, 2001 Conformal Equal Area • • • Mapping System Name: Texas Centric Mapping System/Lambert Conformal Abbreviation: TCMS/LC Projection: Lambert Conformal Conic Longitude of Origin (central meridian): 100° West (-100) Latitude of Origin: 18° North (18) Lower Standard Parallel: 27° 30’ (27. 5) Upper Standard Parallel: 35° (35. 0) False Easting: 1, 500, 000 meters False Northing: 5, 000 meters Datum: North American Datum of 1983 (NAD 83) Unit of Measure: meter • • • Mapping System Name: Texas Centric Mapping System/Albers Equal Area Abbreviation: TCMS/AEA Projection: Albers Equal Area Conic Longitude of Origin (central meridian): 100° West (-100) Latitude of Origin: 18° North (18) Lower Standard Parallel: 27° 30’ (27. 5) Upper Standard Parallel: 35° (35. 0) False Easting: 1, 500, 000 meters False Northing: 6, 000 meters Datum: North American Datum of 1983 (NAD 83) Unit of Measure: meter These projections are also used! “The nice thing about standards is that there are so many to choose from. ” John Quartermain The Matrix They are all available as defined projections in Arc. GIS 9 under State Systems (not the same as State Plane!)

Coordinate Systems: critical required information To correctly use any set of projected data in GIS, the following critical information (metadata) is required at minimum • Datum (required also for data in lat. /long coordinates) • Projection type (Mercator, Lambert conformal conic, etc. ) • Projection parameters For conic and cylindrical – Central meridian – Standard parallel (for tangent) • both standard parallels for secant For azimuthal • Point of contact – Point of origin for coordinate system (often expressed as false easting & northing) • Unit of measurement – Feet, meters, etc. Note: The term geographic projection often used to refer to data in lat/long units. 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals All this info. should be recorded on every printed map, and stored in metadata for digital files! 41

Choosing a Map Projection • Issues to Consider: – extent of area to map: city, state, country, world? – location: polar, mid-latitude, equatorial? – predominant extent of area to map: E-W, N-S, oblique? } detail in Appendix • Rules of thumb – Choose a standard for your organization and keep all data that way. – Also retain lat/long coords in the GIS database if possible – for small areas, projection is less critical and datum is more critical; reverse for large areas – check contract; does it specify a required projection? State Plane or UTM often specified for US gov. work. – use equal-area projections for thematic or distribution maps, and as a general choice for GIS work – use conformal projections in presentations – for navigational applications, need true distance or direction. – Even though modern GIS systems are sophisticated in their handling of projections, you ignore them at your peril!!! 42 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals

The US displayed using a “Geographic Projection” • treats lat/long as X, Y • has no desirable properties other than convenience • don’t do it! 3/18/2018 Ron Briggs, UTDallas Map of State Plane zones Do not do it! GISC 6381 GIS Fundamentals 43

How Arc. GIS Handles Coordinates and Projections • The coordinate reference system of the display view is determined by the first layer opened in the view • • – projection assoc. with entire view, not any one layer – Once Arc. MAp has been informed of the original projection of the data, you can re -project the view. – this applies to the display only. The underlying data files are not changed in any way – To change the underlying data files, use Arc. Catalog • Geographic (lat/long) • Projected (by type and parameters) – This may or may not be known • As other layers are added, they are: – Re-projected “on-the-fly” to that of the view if their reference system and reference system of first layer is known – Displayed “as is” (and thus potentially incorrectly) if either is not know (warning issued) If the projection of the first layer was not already recorded, you must select View/Data Frame Properties and either select Coordinate System tab to specify projection of View • For correct measurement only, you can select General tab – Map Units: may be “unknown” when data read in • user sets it based on actual units for raw data (e. g decimal degrees) – Display units (distance units in AV 3. 2): for reporting measurements (e. g. miles) • map units must be specified before display units can be set • if map units specified incorrectly, distance measures will be wrong!

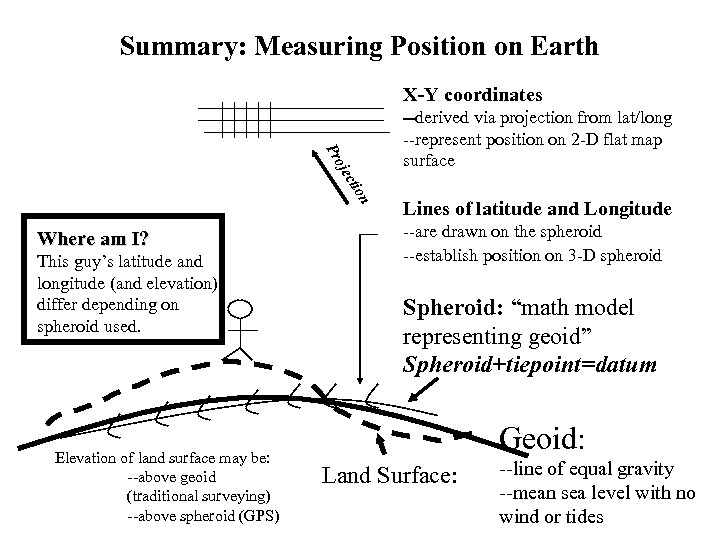Summary: Measuring Position on Earth X-Y coordinates oje Pr --derived via projection from lat/long --represent position on 2 -D flat map surface on cti Where am I? This guy’s latitude and longitude (and elevation) differ depending on spheroid used. Elevation of land surface may be: --above geoid (traditional surveying) --above spheroid (GPS) Lines of latitude and Longitude --are drawn on the spheroid --establish position on 3 -D spheroid Spheroid: “math model representing geoid” Spheroid+tiepoint=datum Geoid: Land Surface: --line of equal gravity --mean sea level with no wind or tides

References on Map Projections and Related Topics • • • Smith, James R. Introduction to Geodesy: The History and Concepts of Modern Geodesy New York, John Wiley, 1997 Yang, Snyder, Tobler Map Projection Transformation: Principles and Applications, Taylor and Frances, 2000 Lev M Bugayevskiy, J. P Snyder Map Projections: A Reference Manual Taylor and Frances, 1995 Snyder, John P. Map Projections--A Working Manual US Geological Survey Professional Paper #1395, 1987 Snyder, John P. Map Projections Used by the US Geological Survey, USGS Bulletin #1532, 2 nd. ed. , 1983 Melita Kennedy and Steve Kopp. Understanding Map Projections: Redlands, CA, ESRI, Inc, 1994 Maling, D. H. Coordinate Systems and Map Projections, London, George Philip, 1973 Robinson, Arthur H. et. al. Elements of Cartography. New York: John Wiley, 5 th ed. , 1995 White, C. Albert A History of the Rectangular Survey System Washington, D. C. USGPO, 1982 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 46

Appendix Projection Reference Materials Useful articles on ESRI's Support Site: FAQ: Where can I find more information about coordinate systems, map projections, and datums? http: //support. esri. com/index. cfm? fa=knowledgebase. techarticles. article. Show&d=17420 FAQ: Projection Basics: What the GIS professional needs to know http: //support. esri. com/index. cfm? fa=knowledgebase. techarticles. article. Show&d=23025 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 47

Map Projections by Property Preserved: Shape and Area • Conformal (orthomorphic) – – – preserves local shape by using correct angles; local direction also correct lat/long lines intersect at 90 degrees area (and distance) is usually grossly distorted on at least part of the map no projection can preserve shape of larger areas everywhere use for ‘presentations’; most large scale maps by USGS are conformal examples: mercator, stereographic • Equal-Area (Equivalent or homolographic)) – – – area of all displayed features is correct shape, angle, scale or all three distorted to achieve equal area commonly used in GIS because of importance of area measurements use for thematic or distribution maps; examples: Alber’s conic, Lambert’s azimuthal 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 48

Map Projections by Property Preserved: Distance and Direction • Equidistant – preserves distance (scale) between some points or along some line(s) – no map is equidistant (i. e. has correct scale) everywhere on map (i. e. between all points) – distances true along one or more lines (e. g. all parallels) or everywhere from one point – great circles (shortest distance between two points) appear as straight lines – important for long distance navigation – examples: sinusoidal, azimuthal • True-direction – – – provides correct direction (bearing or azimuth) either locally or relative to center rhumb lines (lines of constant direction) appear as straight lines important for navigation some may also be conformal, equal area, or equidistant examples; mercator (for local direction), azimuthal (relative to a center point) 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 49

Map Projections by Geometry Planar/Azimuthal/Zenithal • map plane is tangent to (touches) globe at single point • accuracy (shape, area) declines away from this point • projection point (‘light source’) may be – earth center (gnomic): all straight lines are great circles – opposite side of globe (stereographic): conformal – infinitely distant (orthographic): ‘looks like a globe’ • good for polar mappings: parallels appear as circles • also for navigation (laying out course): straight lines from tangency point are all great circles (shortest distance on globe). 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 50

Map Projections by Geometry Conical • map plane is tangent along a line, most commonly a parallel of latitude which is then the map’s standard parallel • cone is cut along a meridian, and the meridian opposite the cut is the map’s central meridian • alternatively, cone may intersect (secant to) globe, thus there will be two standard parallels • distortion increases as move away from the standard parallels (towards poles) • good for mid latitude zones with east-west extent (e. g. the US), with polar area left off • examples: Alber’s Equal Area Conic, Lambert’s Conic Conformal 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 51

Map Projections by Geometry Cylindrical • as with conic projection, map plane is either tangent along a single line, or passes through the globe and is thus secant along two lines • mercator is most famous cylindrical projection; equator is its line of tangency • transverse mercator uses a meridian as its line of tangency • oblique cylinders use any great circle • lines of tangency or secancy are lines of equidistance (true scale), but other properties vary depending on projection 3/18/2018 Ron Briggs, UTDallas GISC 6381 GIS Fundamentals 52

Best Map Projections by Size of Area World/Hemisphere • World - Conformal MERCATOR, TRANSVERSE, OBLIQUE_MERCATOR • World - Equal Area CYLINDRICAL, ECKERTIV, ECKERTVI, FLAT_POLAR_QUARTIC MOLLWEIDE, SINUSOIDAL • World - Equidistant: AZIMUTHAL • World - straight rhumb line: MERCATOR • World - Compromise: MILLER, ROBINSON 3/18/2018 Ron Briggs, UTDallas • Hemisphere - Conformal STEREOGRAPHIC, POLAR • Hemisphere - Equal Area LAMBERT_AZIMUTHAL • Hemisphere - Equidistant AZIMUTHAL • Hemisphere - Global look ORTHOGRAPHIC NAMES correspond to ARC/Info commands GISC 6381 GIS Fundamentals 53

Best Map Projections by Size of Area: continent or smaller • E/W along equator MERCATOR (conformal) CYLINDRICAL (equal area) • E/W away from Equator LAMBERT (conformal) ALBERS (equal area) • North/South TRANSVERSE, UTM (conformal) • Oblique region OBLIQUE_MERCATOR (conformal) • Equal extent all directions POLAR, STEREOGRAPHIC< UPS (conformal) LAMBERT_AZIMUTHAL (equal area) 3/18/2018 Ron Briggs, UTDallas • Straight Great Circle GNOMIC • Correct Scale- between points: TWO_POINT_EQIDISTANT • Correct Scale- along meridians AZIMUTHAL(polar), EQUIDISTNAT, SIMPLE_CONIC • Correct Scale - along parallels POLYCONIC, SINUSOIDAL, BONNE Source: Snyder, 1987 Map Projections - A Working Manual. Workshop Proceedings, 1995 ESRI User Conference, p. 552 GISC 6381 GIS Fundamentals 54

How Arc. View 3. 2 Handles • Coordinates and Projections • all themes in a view must be in same coordinate system (lat/long or projected) • you must know it‘cos Arc. View will read raw data and overlay even if projections differ • A View can be projected only if original data is in Lat/Long decimal degrees – All themes must be in lat/long decimal degrees, and in same datum • – always try to get data in that format – for US “lower 48” states these will range from -125 to -65 (W-E) and 25 to 49 S-N • exception for images: if image is projected, and vector data is in decimal degrees, can set view projection to match image projection and data will overlay correctly • • If raw data in different coord systems, use projection utility external to AV (new in 3. 2) to convert to common coord. system View, Properties used to specify projections and related issues – projection assoc. with view not a theme – Map Units will be “unknown” when data read in • user sets it based on actual units for raw data (e. g decimal degrees) – Distance units are units in which measurements will be reported (e. g. miles) • map units must be specified before distance units can be set • if map units specified incorrectly, distance measures will be wrong! To Project a View – All data must be in decimal degrees and Map Units should be set to this – a variety of projections are available with preset parameters (stan. parallels, etc) • Custom check box available if wish to specify own parameters – re-specify decimal degrees in Map Units to 'cancel' a projection If data already projected, do not specify projection in AV. View won’t draw! To cancel mistake, select Projections of the World, Type: unknown, then click Zoom to Full Extent icon