ТЕРМОГИДРОДИНАМИКА ПЕРЕХОДНЫХ И АВАРИЙНЫХ РЕЖИМОВ РЕАКТОРНЫХ УСТАНОВОК

ТЕРМОГИДРОДИНАМИКА ПЕРЕХОДНЫХ И АВАРИЙНЫХ РЕЖИМОВ РЕАКТОРНЫХ УСТАНОВОК

02 МОДЕЛЬ РАЗДЕЛЬНОГО ТЕЧЕНИЯ ФАЗ Модели многофазного потока

Различные модели многофазной жидкости можно разделить по способу описания структуры исследуемой среды на несколько 03 групп: ● гомогенные (жидкость рассматривается как сплошная среда и описывается единой системой уравнений сохранения (уравнений поля) и соответствующих замыкающих соотношений; наличие различных фаз моделируется введением коэффициентов, учитывающих вклад каждой фазы в теплофизические и реологические свойства жидкости); ● смесевые, или иначе диффузионные (жидкость рассматривается как сплошная среда, для которой формулируются в терминах свойств смеси уравнения поля, которые дополняются диффузионным уравнением, описывающим изменение концентраций фаз); ● модели раздельного течения фаз (для каждой из рассматриваемых фаз формулируется система уравнений сохранения и соответствующих уравнений баланса на межфазных границах).

04 Моделировать с достаточной точностью все режимы гидродинамики и теплообмена многофазного теплоносителя, охлаждающего ТВС ядерного реактора, возможно только в рамках модели раздельного течения фаз.

ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ Тема № 1 Основные положения теории тепломассообмена

ТЕОРЕМА ПЕРЕНОСА Теорема переноса (некоторые называют ее теоремой Лейбница или правилом Лейбница) является обобщением известного из математического анализа правила дифференцирования интеграла по параметру. В случае дифференцирования по времени интеграла по объёму тела (материальному объёму) от некоторой функции координат и времени теорема переноса формулируется так: (37) ________________

Функция Ψ является функцией времени и координат (скаляр, вектор или тензор 2 -го порядка). Интегрирование ведётся по всей области пространства, занимаемой телом в его текущей конфигурации. В общем случае можно ожидать, что предел интегрирования является функцией времени. Рассмотрим это интегрирование (левая часть уравнения (37)) по объёму в исходной конфигурации κ. В этом случае предел интегрирования не зависит от времени и может быть выражен через материальные координаты ограничивающей поверхности. В свою очередь это означает, что в рассматриваемой процедуре можно поменять местами операции дифференцирования и интегрирования. Пусть точки, а – текущие координаты материальной – её материальные координаты. Выполним преобразование левой части уравнения (37).

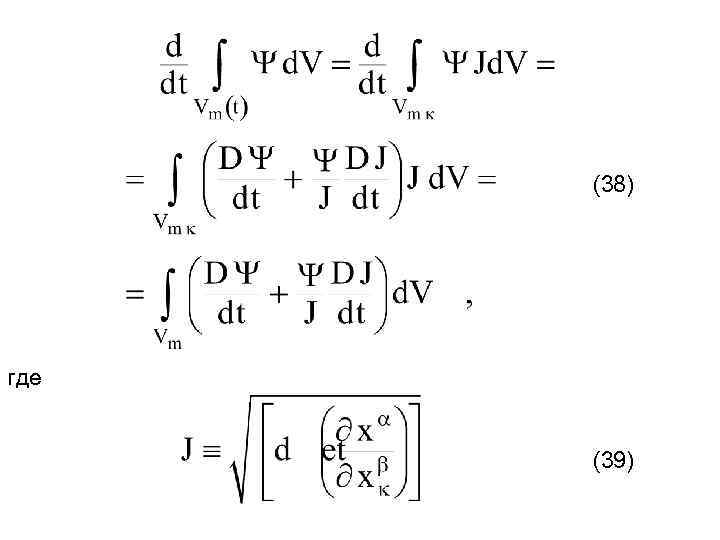(38) где (39)

Величину J можно считать объёмом в текущей конфигурации, отнесённым к единице объёма в начальной конфигурации. Обычно J является функцией как времени, так и координат. Предел интегрирования с пометкой «κ» означает, что интегрирование ведётся по всей области пространства, занимаемой телом в его начальной конфигурации. Определим градиент деформации (40) Примем (41)

54 Легко показать, что (42) Используя определение скорости, получим: (43) (44) _____

Итак (45) Принимая во внимание соотношение (45), уравнение (38) запишем в виде: (37) Используя определение субстанциональной производной уравнение (37) можно переписать в виде (37 а) _______________________

Субстанциональные производные от тензоров 0 -го ранга (скаляра), 1 -го ранга (вектора) и 2 -го ранга: (46)

Применив преобразование Грина (частным случаем которого является теорема о дивергенции или теорема Гаусса), соотношение запишем (37 б) _______________________ где – замкнутая поверхность, ограничивающая объём. Уравнения (37), (37 а), (37 б) – три формы теоремы переноса.

Заменим в выражении (15) материальный объём совпадающим с ним в исходной конфигурации пространственным объёмом , ограниченным поверхностью . Тогда соотношение (37) легко преобразуется к виду (47) ___________________ Выражение (47) называют обобщённой теоремой переноса.

ТЕОРЕМА ПЕРЕНОСА ДЛЯ ОБЛАСТИ, СОДЕРЖАЩЕЙ СИНГУЛЯРНУЮ ГРАНИЦУ Рассмотрим область содержащую сингулярную поверхность (например, границу раздела фаз). Сингулярная поверхность – поверхность, являющаяся разрывной относительно одной или более величин (плотность, скорость и т. п. ). S– V+ S+ u(ξ)ξ Ssing V–

Обобщим теорему переноса на случай, тела содержащего движущуюся границу раздела фаз, которая рассматривается как сингулярная поверхность. Поверхность сингулярна (разрывна) относительно величины и скорости . Поверхность перемещается со скоростью (речь идёт о нормальной компоненте скорости в точке Величины в областях и . непрерывно дифференцируемы и . Так как сингулярная поверхность не является материальной, области и поверхности также не являются материальными.

Определим поле (48) – единичный вектор, перпендикулярный поверхности и направленный из области в область .

Можем записать выражение (49)

К каждому слагаемому правой части соотношения (49) можно применить обобщённую теорему переноса. В результате сформулируем выражения (50 а)

(50 б) Здесь и – предел функции , когда точка приближается к лежащей на сингулярной поверхности точке оставаясь при этом в или , соответственно.

Подставив (50 а) и (50 б) в (49), получим: (51) (52) (51) – теорема переноса для областей, содержащих сингулярные границы. (52) – скачок величины на сингулярной границе.

Дифференциальная форма законов сохранения МАССЫ, ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ), МОМЕНТА ИМПУЛЬСА, ЭНЕРГИИ

ЗАКОН СОХРАНЕНИЯ МАССЫ (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ) Применив к соотношению (19) теорему переноса в форме (37), получим (53) Поскольку предел интегрирования выбран произвольно, (53) справедливо для любого тела или части тела (так как часть тела есть тело). По этой же причине равенство (53) выполняется, если равно нулю подынтегральное выражение, то есть

(54) Воспользовавшись определением субстанциональной производной, уравнение (54) можно записать в виде (55) Формулы (54) и (55) – две формы закона сохранения массы в дифференциальном виде – уравнения неразрывности. (55) – дивергентная форма.

Если плотность не зависит от времени (изохорический процесс) уравнение (55) принимает вид (56) Если плотность не зависит от времени и координат (несжимаемая жидкость) уравнение (56) сводится к (57) Несжимаемость жидкости – достаточное (но не необходимое) условие изохоричности.

ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ) (27) Уравнение сохранения импульса в дифференциальной форме можно получить из первого закона Эйлера (27), применив теорему переноса и уравнение неразрывности. С учетом выражений (37) и (54) левую часть уравнения (27) преобразуем следующим образом: (58)

Первое слагаемое правой части уравнения (27), используя выражение (28) и преобразование Грина, сформулируем так (59) Приняв во внимание соотношения (58) и (59), из (27) получим (60) Ввиду того, что объём произволен, приходим к выводу о справедливости следующего выражения: (61)

Это и есть искомое дифференциальное уравнение сохранения импульса, которое также называют уравнением движения в напряжениях, или первым законом Коши. Учитывая определение субстанциональной производной, выражение (61) сформулируем в виде (62) Умножив уравнение неразрывности (55) скалярно на вектор скорости и сложив с (62), получим (63) Введем в рассмотрение тензор дополнительных напряжений который зададим так: , (64)

где – термодинамическое давление, ; – единичный тензор. Теперь соотношение (63) перепишем в виде (65) Это дивергентный вид сохранения импульса. дифференциального уравнения

ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ) (30) Уравнение сохранения момента импульса в дифференциальной форме получим из второго закона Эйлера (уравнение(30)), применив теорему переноса и уравнение неразрывности. ия зуя часть выражения (30) следующим образом:

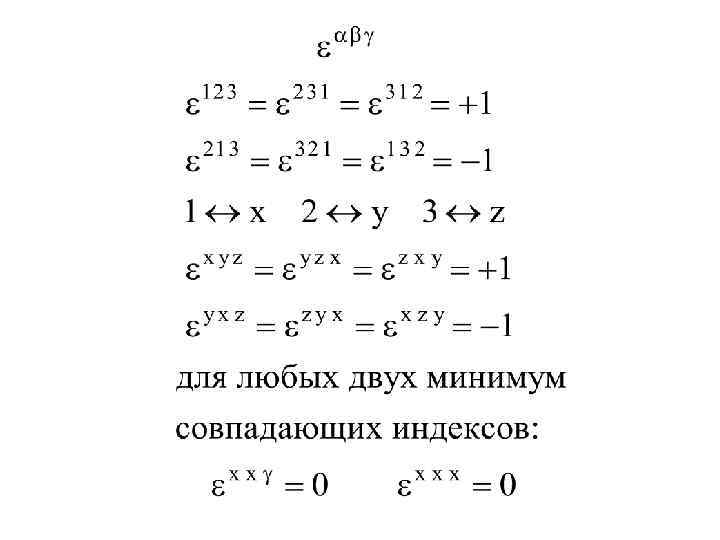
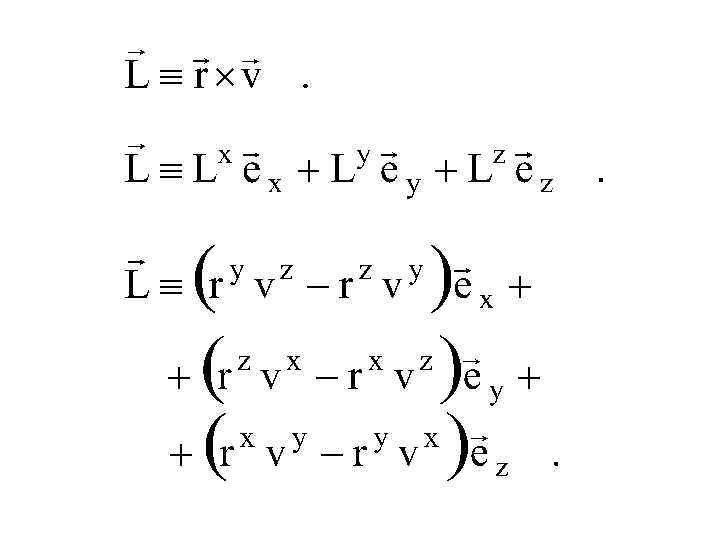
(66) Первое слагаемое правой части уравнения (30), применяя соотношение (28) и преобразования Грина, представим в виде (67) Применяя (66) и (67), уравнение (30) запишем как

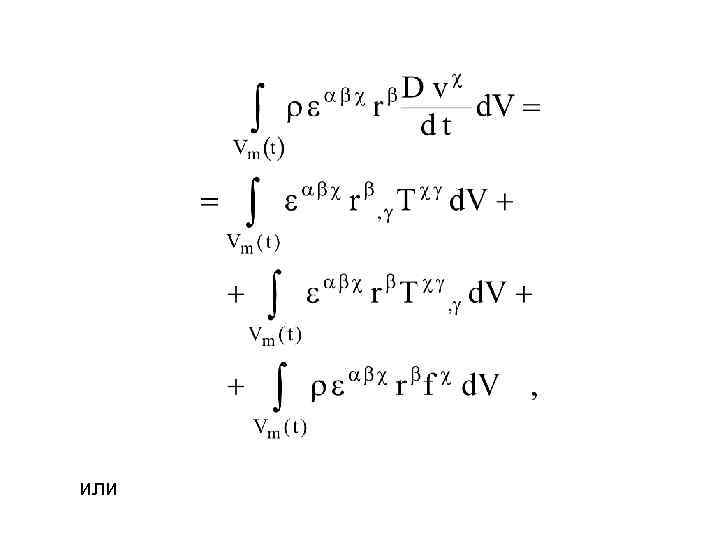или

(68) Вследствие того, что объём интегрирования выбран произвольно, подынтегральное выражение в (68) равно нулю. Следовательно, (69)

Преобразуем это соотношение, используя формулу (54). В результате получим выражение (70) Вернёмся к соотношению (69). Принимая во внимание уравнение (61), приходим к выводу, что (71) Так как где – символ Кронекера, соотношение (32) преобразуется как

(72) Можно также записать (73 а) откуда следует (73 б) Уравнения (73 а) и (73 б) – два варианта записи закона сохранения момента импульса в дифференциальной форме; их также называют вторым законом движения Коши. Из соотношений (73) следует, что в случае, когда все моменты вращения, действующие на тело, являются результатом действующих на тело сил, необходимым и достаточным условием сохранения момента импульса является симметричность тензора напряжений: (74)

ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ (36) ______________________

Из соотношения (36), используя теорему переноса, преобразование Грина и уравнение неразрывности, получим дифференциальное уравнение сохранения энергии. Преобразуем, приняв во внимание соотношения (37) и (54), левую часть выражения (36): (75)

Применяя преобразование Грина и свойство симметрии тензора напряжений, первый член в правой части уравнения (36) представим в виде объёмного интеграла: (76) – вектор плотности потока энергии, Теперь представим контактный перенос энергии так: (77)

Получим (78) Учитывая соотношения (75), (76) и (78), уравнение (36) запишем в виде

Так как объём, по которому выполняется интегрирование, выбран произвольно, равенство верно, если равно нулю подынтегральное выражение, т. е. справедливо уравнение (79) Это одна из форм дифференциального уравнения сохранения энергии.

Используя формулу (54), преобразуем (79) к виду Окончательно имеем (80) _________________________

Если умножить скалярно на вектор скорости уравнение первого закона Коши (61), то получим (81) Вычитая это соотношение из уравнения (79), получим дифференциальное уравнение баланса внутренней энергии (82) или (82 а)

– удельная энтальпия, . Запишем дифференциальное уравнение сохранения энергии в терминах энтальпии : (84)

Перейдя от субстанциональной производной к частным производным и использовав уравнение неразрывности (55), получим дивергентный вид дифференциального уравнения сохранения энергии в терминах энтальпии (85)

ОБЩИЕ УРАВНЕНИЯ БАЛАНСА Полученные выше интегральные уравнения сохранения можно рассматривать как частные случаи уравнения, которое, как правило, называют общим интегральным уравнением баланса. Оно имеет вид (86) Аналогично, дифференциальные уравнения сохранения можно рассматривать как частные случаи уравнения, которое принято называть общим дифференциальным уравнением баланса (87)

– характерная для исследуемой субстанции некоторая "транспортная" величина (удельная); вливающий – неконвективные приток/утечку поток субстанции (тензор, порядок которого на единицу больше порядка тензора ); удельная – мощность генерации субстанции (тензор того же порядка, что и тензор ). Если в качестве выбирается не просто скаляр (переменная), а некоторая константа (например, единица), то и полагаются тождественно равными нулю. Теперь легко заметить, как необходимо выбирать , чтобы получить то или иное уравнение сохранения. и ,

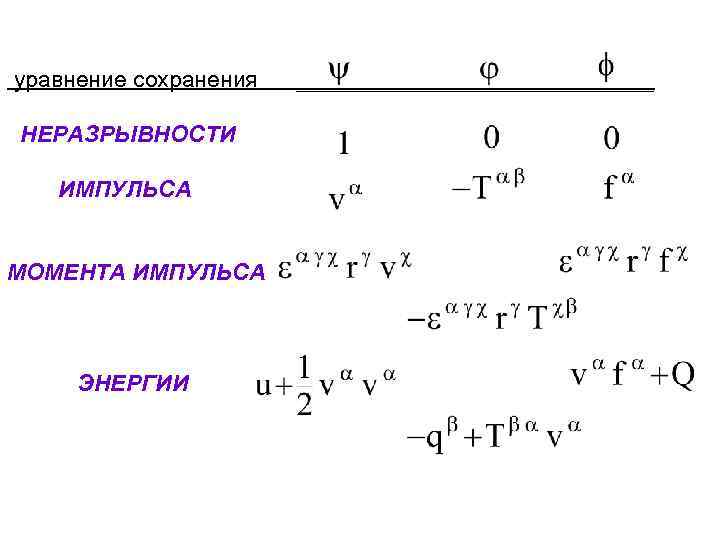уравнение сохранения НЕРАЗРЫВНОСТИ ИМПУЛЬСА МОМЕНТА ИМПУЛЬСА ЭНЕРГИИ ______________

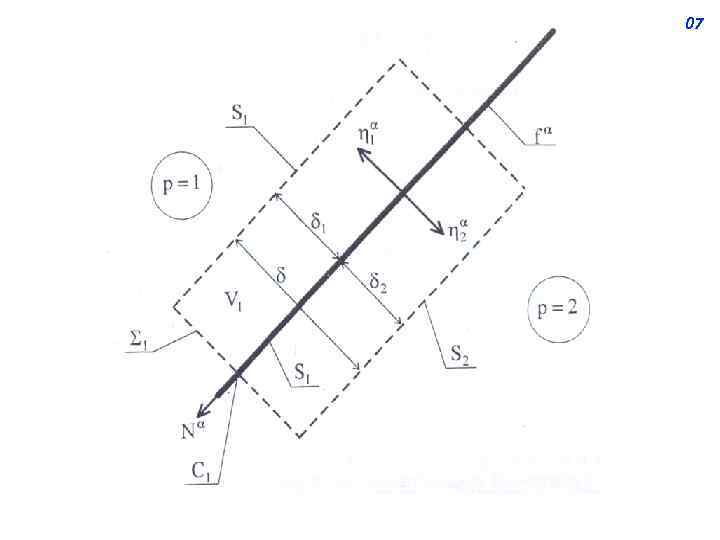
05 Уравнения баланса на границе раздела фаз Дифференциальные уравнения баланса могут использоваться при описании течения многофазного теплоносителя с помощью модели раздельного течения фаз, в рамках которой каждая из фаз рассматривается как самостоятельный континуум. Эти уравнения могут быть применены к каждой из фаз вплоть до межфазной поверхности. Но для описания процессов на границе раздела фаз необходимо получить соответствующий уравнения баланса. Будем рассматривать межфазную границу как сингулярную поверхность, поперек которой плотность, энергия и скорость жидкости терпят конечные скачки (разрывы). Получаемые в результате уравнения принято называть условиями скачка. Условия скачка впервые были получены Н. Е. Кочиным как условия динамического согласования для ударных волн и известны как теорема Кочина. Применительно к межфазной поверхности условия скачка были получены различными авторами [113, 114, 116, 121, 122] путем "расширения" теоремы Кочина за счёт введения в рассмотрение линейных потоков на границе раздела фаз. Наиболее корректно эта задача решена Иши (Ishii) [114] и Дэлэем (Delhaye) [116].

06

07

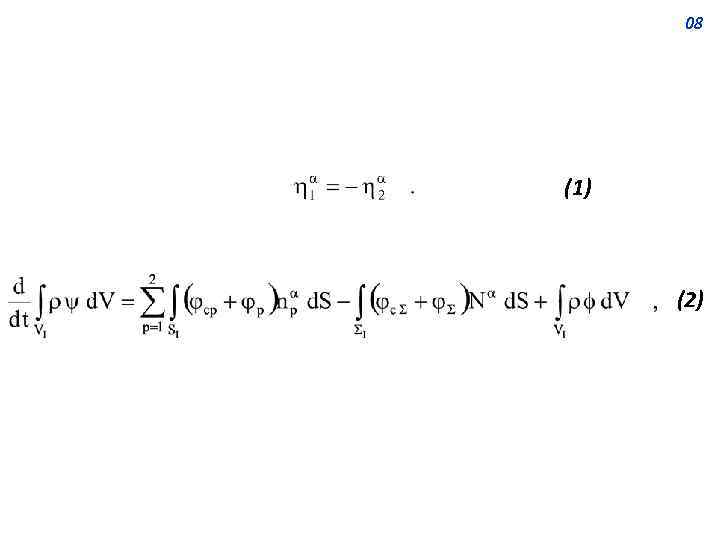08 (1) (2)

09 (3)

10 (4) (5)

11 Используя формулы (3) – (4), выражение (2) запишем как (6) Заменим в уравнении (6) объёмные интегралы поверхностными. С этой целью определим поверхностные свойства. Поверхностная плотность определяется сооотношением (7)

Средняя масса единицы площади рассматриваемого слоя равна 12 (8) Поверхностная скорость задаётся соотношением (9) т. е. (9 а)

Аналогично определим поверхностные значения и (10) (11) Скорость межфазной поверхности может быть представлена как сумма её нормальной и тангенциальной составляющих: (12) 13

14 где а (13) (14) Таким образом, нормальная составляющая задается через скорость перемещения поверхности а тангенциальная – как средняя по толщине рассматриваемого слоя тангенциальная скорость жидкости. Так как единичный вектор лежит в тангенциальной плоскости и нормален к имеем (15)

15 Из уравнений (7), (9) и (15) получим (16) и (17) Применяя уравнения (6) и (17), определим средний линейный конвективный поток вдоль как (18)

16 Преобразуем интегральное уравнение баланса для межфазной поверхности к виду (19) Второе слагаемое правой части выражения (19) представим как

17 Третье слагаемое преобразуется следующим образом: Теперь соотношение (19) запишем в виде (20)

Получим из выражения (20) дифференциальное уравнение баланса для межфазной поверхности. Для этого воспользуемся поверхностными теоремами переноса и Грина. Поверхностная теорема переноса формулируется следующим образом: (21) где означает субстанциональную производную по времени с поверхностной скоростью , т. е. 18

19 (22) а – так называемая поверхностная дивергенция, отличающаяся от обычной тем, что дифференцирование проводится по двум ("б" принимает два, а не три значения) поверхностным координатам. Для обозначения поверхностных координат используем в качестве тензорных индексов строчные буквы кириллицы, отличные по написанию от латинских. Поверхностную теорему Грина сформулируем в виде

(23) Здесь – поверхностный метрический тензор, – пространственный метрический тензор, – смешанный тензор перехода между поверхностными и пространственными координатами, – поверхностная ковариантная производная. Отметим кроме этого, что если имеет только тангенциальную компоненту, то 20

(24) Так как 21 предполагается достаточно малым, считаем, что поверхности и геометрически совпадают с . Теперь уравнение (20) преобразуется к виду (25)

22 Уравнение (25) справедливо для любого участка межфазной поверхности площадью при условии, что Поскольку может быть выбрано сколь угодно малым (вследствие сингулярности межфазной поверхности) из (25) следует, что справедливо уравнение (26)

23 Этот результат совпадает с полученным Дэлеем, хотя использованный метод и определение скорости межфазной поверхности различны.

24 Определим величины (27) и (28) Учитывая определения (10) и (11), запишем для соответственно, выражения и (29) и (30) ,

Применяя определения (27) и (28), уравнение (26) представим в виде 25 (31) Это и есть общее дифференциальное уравнение баланса на межфазной поверхности. Левая часть учитывает скорость изменения в системе отсчета связанной с межфазной границей (движущейся со скоростью ) и влияние перемещения поверхности раздела фаз. Первое слагаемое в правой части – сумма потоков из объёмов фаз, второе – линейный поток вдоль межфазной поверхности, третье – поверхностный источник.

26 Из соотношения (31) получим выражения для скачков величин на межфазной поверхности. Сделаем несколько дополнительных предположений, которые согласуются с используемым допущением о достаточной тонкости межфазного слоя: (32)

27 Первое – массовая плотность межфазной границы пренебрежимо мала, как следствие, ее импульсом и кинетической энергией также можно пренебречь. Второе – пренебрегаем всеми молекулярно-диффузионными потоками вдоль границы фаз, т. е. пренебрегаем поверхностными вязким трением и тепловым потоком. Третье – пренебрегаем поверхностными источниками. В таком случае дифференциальное уравнение баланса на межфазной границе (31) примет вид

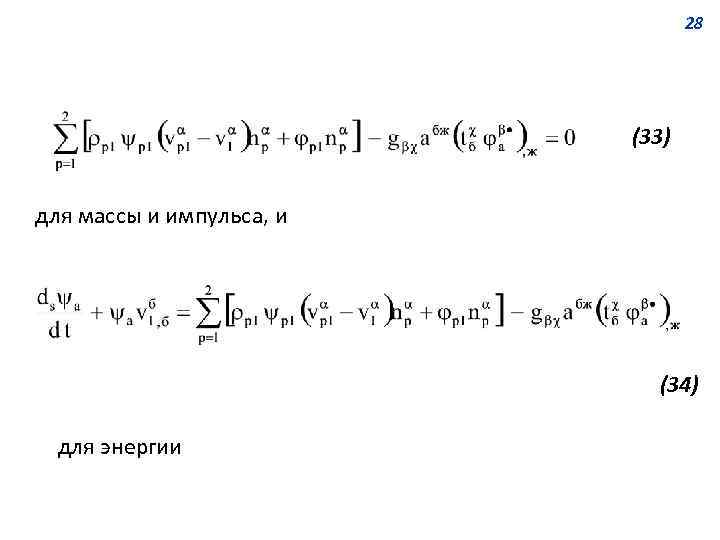28 (33) для массы и импульса, и (34) для энергии

29 2) Уравнение баланса массы на межфазной границе. Межфазный баланс массы получим из уравнения (33), приняв (см. таблицу 1) В результате искомое уравнение запишем следующим образом: (36)

30 Определим межфазный поток массы из р-фазы как (35) Из соотношения (33) имеем (36) Это уравнение констатирует отсутствие производства массы на межфазной поверхности.

31 3) Уравнение баланса импульса на межфазной границе. Межфазный баланс импульса получим из уравнения (33), приняв (37) Полагаем, что поток импульса вдоль межфазной поверхности постоянен и имеет только тангенциальную составляющую. В таком случае справедливо соотношение (24), которое запишем, используя коэффициент поверхностного натяжения , в виде

32 (38) Теперь выражение (37) примет вид (39) Применяя определение (35) межфазного потока массы из р-фазы, соотношение (39) перепишем следующим образом: (40)

4) Уравнение баланса энергии на межфазной границе. 33 Приняв уравнение (33) запишем в виде (41)

34 Так как молекулярно-диффузионными потоками (в том числе – тепловым потоком) на межфазной поверхности пренебрегаем, то второе слагаемое левой части уравнения (41) можем, проделав выкладки аналогичные (35), преобразовать к виду (42) В результате уравнение баланса энергии на межфазной границе можно записать следующим образом: (43)

35 Используя определение (35), соотношение (43) запишем так: (44) Поверхностные уравнения баланса, как и пространственные, должны дополняться замыкающими уравнениями. Связывающее внутреннюю энергию с энтропией и удельным объёмом (плотностью) уравнение состояния с учетом того, что массой межфазной поверхности пренебрегаем, имеет вид (45)

36 плотность удельной внутренней энергии межфазной поверхности (удельная внутренняя энергия единицы площади межфазной поверхности), плотность удельной поверхности. энтропии межфазной Зададим поверхностное термодинамическое давление (поверхностное натяжение) как (46)

37 где температура определяется следующим образом: (47) В дифференциальной форме уравнение (45) принимает вид (48)

38 Соотношение Гиббса-Дюгема задается как (49) Плотность удельной энтальпии межфазной поверхности определим так: (50) Из уравнения (49) имеем (51)

39 Подставив это в (48), получим (52) Комбинируя выражения (46) и (49), находим (53) (54)

40 Таким образом, из соотношений (53) и (54) следует, что для замыкания полученных уравнений баланса на межфазной поверхности, в рамках сделанных допущений о ее свойствах, достаточно теплового уравнения состояния: (55) Подставив результат (53) в уравнение (44), получим (56)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СОХРАНЕНИЯ ДЛЯ ТУРБУЛЕНТНОГО СЖИМАЕМОГО ТЕПЛОНОСИТЕЛЯ 41 Методы усреднения уравнений сохранения, описывающих турбулентный поток При описании турбулентного потока используются, как предложено Рейнольдсом, усреднённые по времени уравнения сохранения. При этом интервал усреднения выбирается достаточно большим по сравнению с характерным временем турбулентных пульсаций.

42 Турбулентная величина и времени , являющаяся функцией координат (57) представляется как сумма макроскопической составляющей и флуктуации а именно: (58)

43 Среднее значение турбулентной величины определяется следующим образом: (59) Очевидно, что (60)

44 Для средних значений справедливы также следующие соотношения: (61)

Полагаем, что макроскопическая составляющая равна своему среднему значению: (62) Из этого не следует равенство среднего значения турбулентной величины и среднего значения её макроскопической составляющей: (63) 45

46 Существуют два метода определения макроскопических составляющих. В обоих макроскопическая составляющая плотности полагается равной среднему значению плотности: (64)

47 Если в качестве макроскопической составляющей выбрано среднее значение величины, условимся флуктуационную составляющую обозначать двумя штрихами вверху: Можем записать: (65) Учитывая соотношения (60), из выражения (65) получим (66)

48 Аналогичное представление используется для давления: (67) (68)

Макроскопические составляющие скорости и энергии 49 (энтальпии) могут быть представлены ● таким же образом (этот метод усреднения назовем первым), либо ● как массово взвешенные величины. Второй метод, который будет применяться в дальнейшем, позволяет избавиться в усреднённых уравнениях сохранения от членов, содержащих усреднённый массовый поток, обусловленный турбулентностью. Флуктуацию турбулентной величины в этом случае будем обозначать одним штрихом вверху:

50 Таким образом, для скорости, внутренней энергии и энтальпии можем записать, соответственно, следующие выражения: (69) (70) (71) где макроскопические составляющие определяются как (73) (72) (74)

51 Заметим, что в этом случае (75) (76) (77)

52 Для несжимаемой жидкости и, следовательно, для некоторой турбулентной величины справедливы тождества (78) (79) т. е. для несжимаемой жидкости оба метода усреднения эквивалентны.

53 Можем записать выражения (80) следовательно, имеет место соотношение (81) Преобразуем (81) к виду

– коэффициент корреляции между величинами Таким образом, справедливо соотношение (82) из которого следует, что оба метода усреднения эквивалентны, когда все коэффициенты корреляции равны нулю. 54

56 Поскольку для сжимаемой жидкости применение второго метода усреднения позволяет, как уже отмечалось, исключить ряд членов в уравнениях сохранения, а также делает более ясной физическую интерпретацию получаемых усреднённых уравнений, далее будем использовать второй метод усреднения.

Дифференциальные уравнения сохранения для турбулентного режима течения 1) Усреднённое по времени уравнение неразрывности. (а) Применяя правила (61) получим из уравнения (а) (83) Второе слагаемое можно преобразовать, используя выражение (72). В результате получим искомое уравнение: (84) 57

58 Усреднённое по времени уравнение сохранения импульса Выполним усреднение уравнения (26). (б) Запишем, используя соотношения (61), следующее выражение: (85) Представим первое слагаемое левой части уравнения (85) в виде (86)

Второе слагаемое левой части преобразуем следующим образом: 59 (87) Полагая , третье слагаемое правой части представим как (88) Учитывая соотношения (86) – (88), выражение (85) запишем в виде (89)

Взятое со знаком минус выражение, стоящее под знаком производной в третьем слагаемом левой части уравнения (89), принято интерпретировать как тензор турбулентных напряжений: 60 (90) Теперь можем окончательно записать усредненное по времени уравнение сохранения импульса (91)

61 Усреднённое по времени уравнение сохранения энергии Преобразуем уравнение (92) используя определение субстанциональной производной и уравнение неразрывности (а).

62 Усредним по времени уравнение (92): (93) Преобразуем шестое слагаемое левой части уравнения (93): (94)

63 Теперь уравнение (93) запишем в виде (95) Введём в рассмотрение виртуальную внутреннюю энергию которая является массово взвешенной величиной равной сумме массово взвешенных удельных внутренней энергии и кинетической энергии турбулентности , определяемой как

64 (96) Таким образом, для имеем (97) Запишем уравнений (97) в терминах виртуальной внутренней энергии: (98)

65 Определим вектор турбулентной теплопроводности следующим образом: (99) Теперь, учитывая определение (90), уравнение (97) запишем в виде (100)

66 Поскольку справедливы соотношения (101) (102) получим выражение (103)

67 которое запишем, используя определение (г) так (104)

68 Если из уравнения (103) вычесть умноженное на усреднённое по времени уравнение сохранения импульса (91), то получим уравнение для виртуальной внутренней энергии: (105) Определим, по аналогии с (97), виртуальную энтальпию (106)

Теперь можем записать усреднённое по времени уравнение энергии в терминах виртуальной энтальпии: 69 что эквивалентно (107)

70 УРАВНЕНИЯ БАЛАНСА НА ГРАНИЦЕ РАЗДЕЛА ФАЗ ДЛЯ ТУРБУЛЕНТНОГО РЕЖИМА ТЕЧЕНИЯ Усреднённое по времени уравнение баланса массы на межфазной границе Усредним по времени уравнение баланса массы на межфазной поверхности (34). Заметим, что (108) Выполнив эквивалентные преобразования, получим (109)

71 Обозначив, по аналогии с (35), (110) окончательно запишем (111)

72 Усреднённое по времени уравнение баланса импульса на межфазной границе Выполним усреднение уравнения баланса импульса на межфазной границе (39). Используем при этом уравнения (г), (62), (65) – (70), (87) и (90). Получим (112)

73 Обозначив (113) и замечая, что (114) перепишем выражение (112) в виде (115)

74 Из соотношения (158) следует, что (116) Вычитая (116) из (115), получим (117)

Усреднённое по времени уравнение баланса энергии на межфазной границе 75 Усредним уравнение баланса энергии на межфазной границе (43). Используем при этом уравнения (г), (61), (65) – (69), (72), (80), (87) и (90). Получим (118)

76 Применяя соотношения (107) и (113), преобразуем второе слагаемое правой части выражения (117): (119) Выражение, стоящее под знаком суммы, в первом слагаемом правой части соотношения (117) запишем в виде (120)

77 Сформулируем выражение, заключённое в (120) в квадратных скобках, как (121) Третье слагаемое в соотношении (121), проделав выкладки аналогичные (94), запишем в виде (122)

78 Четвертое слагаемое в соотношении (121), учитывая выражение (87), преобразуется так: (123) Используя соотношения (121) – (123), определения (89), (95), (96) и (98), правую часть выражения (120) запишем следующим образом: (124)

79 Подставляя (119) и (124) в (118), окончательно получим (125)

80 Если условия задачи позволяют пренебречь поверхностным натяжением, уравнение (125) можно переписать в виде (126) Определим удельную энергию межфазной поверхности как (127)

81 и перепишем выражение (125): (128) Если пренебречь поверхностным натяжением, уравнение (128) сведется к (129)

82 Используя определение (106) виртуальной энтальпии, соотношение (127) запишем в окончательном виде (130)

83 Способы усреднения дифференциальных уравнений сохранения по времени и по пространству при описании гетерогенных сред

84 Стремясь описать поведение реальной жидкости (газа) в рамках механики сплошной среды, используя полученные из интегральных законов сохранения массы, импульса, момента импульса и энергии дифференциальные уравнения сохранения неизбежно приходится столкнуться с проблемой усреднения указанных уравнений, которые справедливы для мгновенных значений входящих в них величин, т. е. для значений в некоторый конкретный момент времени. Необходимость усреднения объясняется, в частности, наличием турбулентных пульсаций. Для многофазных жидкостей добавляется также то обстоятельство, что рассматриваемая область пространства не может считаться гомогенной средой, так как содержит фрагменты различных фаз, разделённых межфазными границами, рассматриваемыми как сингулярные поверхности, на которых свойства жидкости и параметры потока терпят разрывы.

85 Некоторые авторы [1, 2, 3] вначале проводят усреднение по пространству дифференциальных уравнений для мгновенных значений, а затем выполняют усреднение по времени полученных пространственно-усреднённых уравнений. 1. Вернье, Ф. Общие уравнения двухфазных потоков в применении к термогидродинамике кипящих ядерных реакторов / Ф. Вернье, Ж. М. Делэй // Новые исследования по общим уравнениям гидродинамики и энергии двухфазных течений. – М. : Атомиздат, 1970. – С. 1– 64. 2. Делайе, Дж. Теплообмен и гидродинамика двухфазных потоков в атомной и тепловой энергетике / Дж. Делайе, М. Гио, М. Ритмюллер. – М. : Энергоатомиздат, 1984. – 424 с. 3. Нигматулин, Р. И. Динамика многофазных сред: в 2 ч. / Р. И. Нигматулин – М. : Наука. Гл. ред. физ. -мат. лит. , 1987. – Ч. 1. – 464 с.

86 Другой подход [4, 5, 6, 7, 8] состоит в том, что выполняется усреднение по времени, при котором учитывается не только турбулентный характер течения, но и гетерогенная структура среды. 4. Ishii, M. Thermo-Fluid Dynamic Theory of Two-Phase Flow / M. Ishii. – Paris: Eyrolles, 1975. – 284 p. 5. Chawla, T. C. Two-fluid model of two-phase flow in a pin bundle of a nuclear reactor / T. C. Chawla, M. Ishii // International Journal of Heat and Mass Transfer. – 1980. – Vol. 23, № 7. – P. 991– 1001. 6. Телетов, С. Г. Гидродинамика двухфазных смесей. 1. Уравнения гидродинамики и энергии / С. Г. Телетов // Вестник Московского университета. Сер. 1. Механика. – 1958. – № 2. – С. 15– 28. 7. Standart, G. The mass, momentum and energy equations for heterogeneous flow systems / G. Standart // Chemical Engineering Science. – 1964. – Vol. 19, № 3. – P. 227– 236. 8. Семенович О. В. К проблеме термогидродинамического расчета стержневых тепловыделяющих сборок. Уравнения модели раздельного течения фаз / О. В. Семенович. ‒ Препринт ИПЭ НАН Беларуси, № 50. Минск, 1999. – 75 с.

87 Авторы работы [2] показали, что и один и другой подходы дают в итоге эквивалентные уравнения. Использование второго из указанных методов усреднения дифференциальных уравнений сохранения для мгновенных значений представляется более предпочтительным, так как при решении практических задач, формулируя систему уравнений математической модели, приходится, как правило, выполнять пространственное усреднение дифференциальных уравнений сохранения. По этой причине, в частности, именно такой подход применяется большинством авторов при выводе системы решаемых уравнений в математических моделях гидродинамики и теплообмена в реакторных установках.

88 Процедуру усреднения по времени дифференциальных уравнений сохранения и условий баланса на межфазных границах можно выполнять так, как это сделано в работе [4]. Поступим несколько иначе [8], и используем в качестве усредняемых уравнения сохранения (131), (132) и (133), а также усреднённые по времени уравнения баланса на межфазной поверхности (134), (135) и (136). Такой подход выбран потому, что, во-первых, первая стадия предлагаемой процедуры усреднения уже выполнена в на предыдущей лекции, и, во-вторых, он более нагляден.

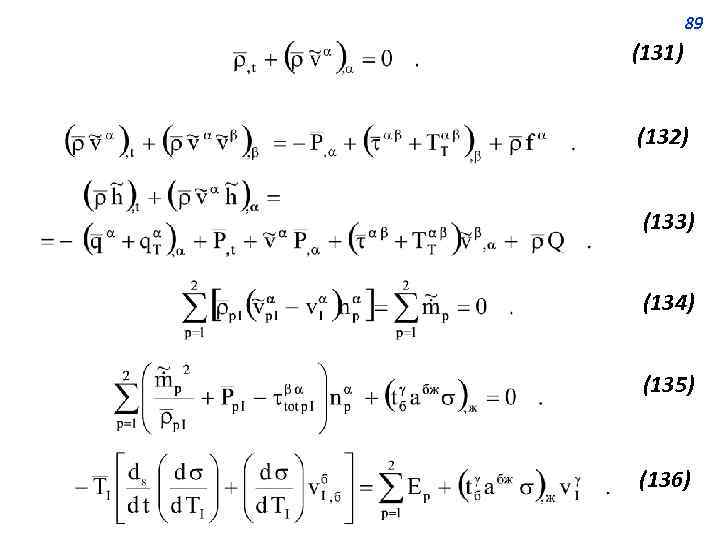89 (131) (132) (133) (134) (135) (136)

90 УРАВНЕНИЯ МОДЕЛИ РАЗДЕЛЬНОГО ТЕЧЕНИЯ ФАЗ

Фазовые уравнения баланса

91 Методика усреднения Рассмотрим некоторую точку пространства с координатами. Выберем временной интервал усреднения равным В течение времени в точке . могут попеременно находиться как любая из рассматриваемых фаз, так и межфазная поверхность. Чтобы учесть вклад каждой фазы в среднее значение, введем в рассмотрение фазовую функцию определяемую следующим образом: ,

92 (137) В работах [4, 8] показано, что среднее за интервал значение фазовой функции равно значению объёмного содержания фазы в рассматриваемой жидкости: (138)

93 Используя фазовую функцию в качестве весовой функции, определим фазово-среднее значение величины : (139) Из (9) следует, что (140) С другой стороны (141)

Проделав очевидные манипуляции с соотношениями (140) и (141), легко получить (142) а так как (143) то окончательно можем записать (144) 94

95 Аналогично (145) Рассмотрим вопрос об усреднении поверхностных переменных, определяющих свойства межфазной поверхности. Пусть некоторые межфазные поверхности (их суммарное количество обозначим в течение промежутка времени проходят через заданную точку . Если скорость j-й (из числа J) межфазной поверхности есть то нормальная составляющая равна (146) ,

96 За время Δt рассматриваемая межфазная поверхность сместится по направлению нормали на расстояние , равное (147) (139)

97 (148) Введем в рассмотрение величину , определяемую как (149) Определение (148) сформулируем теперь в виде (150)

98 В работе [4] для фазово-средних значений производных по времени получено следующее выражение: (151) Из соотношений (141) и (151) следует

99 (152 а) и (152 б) Для фазово-средних значений пространственных производных там же получено выражение (153)

100 из которого следует (154 а) и (154 б)

Фазовые уравнения баланса субстанции 101 Общее фазовое уравнение баланса (131, 132 и 133). (155) (156) (157) (155 и 157), 1 3 2

102 (128) Определим (*) Применяя определения (137), (*), (155) и (156), запишем уравнение (133) следующим образом: (159)

Очевидно, что уравнения (131), (158) и (159) можно рассматривать как различные формы уравнения 103 (160) (131) (158) (159) (160)

(161) 104 (154), Используя соотношения (152) и (24), выполним усреднение (22) (161) уравнения (31) по фазе. Получим (162) Определим (163)

105 Запишем окончательно общее дифференциальное фазовое уравнение баланса (164)

106 Фазовое уравнение баланса массы Взяв необходимые данные в таблице и применив определение (163), представим уравнение (164) в виде (135) (**) Используя определение (**), запишем это соотношение следующим образом: (136)

107 Применив определение (147), преобразуем выражение (166): (167) Отсюда, выполнив простые определение (150), получим манипуляции и применив (168)

108 Обозначим (169) Выражение (168) примет вид (170) Введем в рассмотрение величину , определяемую как (171)

109 Используя определение (171), запишем окончательно уравнение сохранения массы р-фазы (172)

Фазовое уравнение баланса импульса 110 Используя данные второй строки таблице и определение (163), преобразуем уравнение (164) к виду: (173) Применив определение (*) и перегруппировав члены, получим

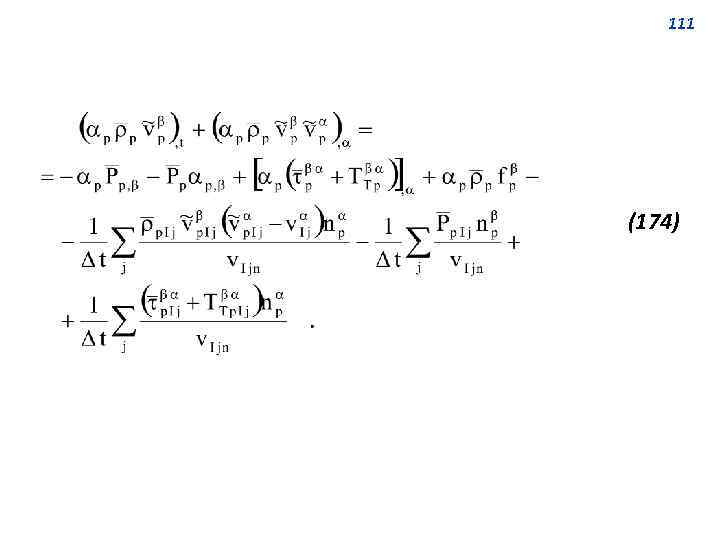111 (174)

112 Определим величины: (175) (176) (177) (178)

113 Введем в рассмотрение вектор (179) Перепишем уравнение (174): (180)

114 Из соотношения (153), при Ψ=1, имеем (181) Непосредственно из определения (137) следует, что (182) Таким образом, получим из (182) выражение для градиента

115 (183) Запишем уравнение (180) запишем следующим образом: (184)

116 Определив (185) сформулируем фазовое уравнение импульса в окончательном виде баланса (186)

117 Фазовое уравнение баланса энергии Подставив в выражение (184) соотношения из таблицы, получим фазовое уравнение баланса энергии: (187)

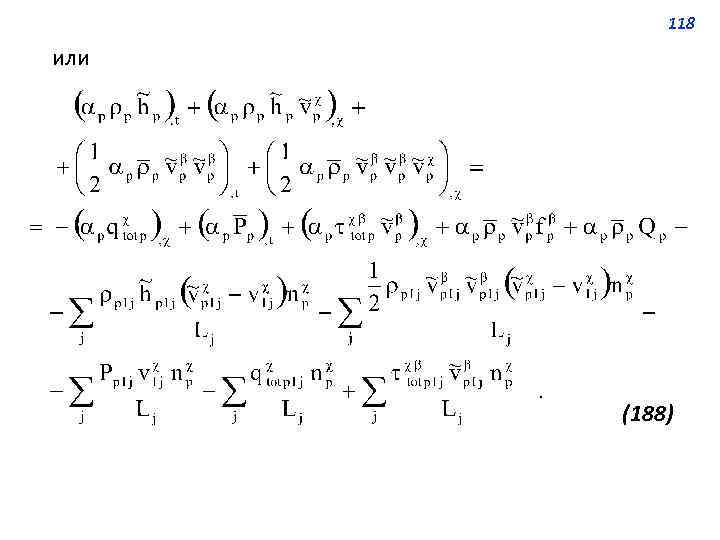118 или (188)

Преобразуем сумму третьего и четвертого слагаемых левой части: 119 (189)

120 Перепишем выражение (188): (190)

121 Вычитая из соотношения (190) умноженное на равенство (186), получим (191)

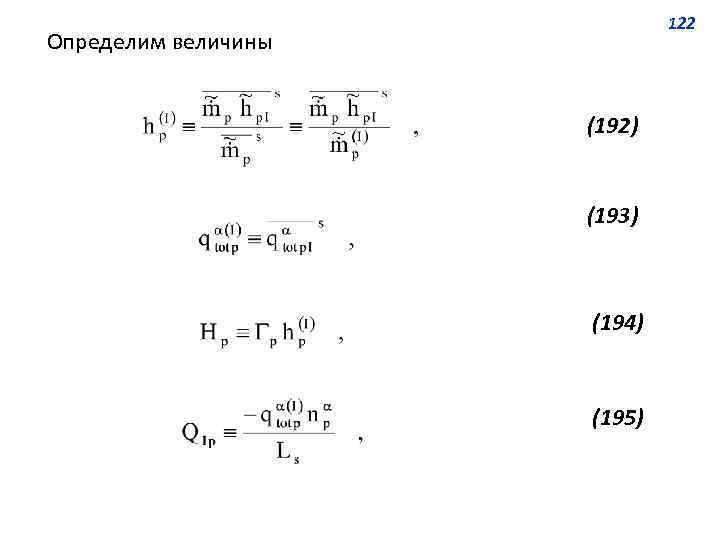122 Определим величины (192) (193) (194) (195)

123 (196) и (197)

124 Используя соотношения (192)–(197), запишем формулу (191) так: (198)

125 Окончательно, сформулируем фазовое уравнение баланса энергии в виде (199) где (200)

126 УСЛОВИЯ БАЛАНСА НА ГРАНИЦЕ РАЗДЕЛА ФАЗ Общее фазовое уравнение баланса на межфазной поверхности Полученные ранее (предыдущая лекция) уравнения баланса на межфазной границе представляют собой различные формы уравнения, которое назовем общим уравнением баланса на межфазной поверхности и сформулируем следующим образом: (201)

(201). 127 (155). (150) (201).

128 (202) что легко преобразуется к виду (203) Определим (204)

129 и запишем окончательно общее фазовое уравнение баланса на межфазной поверхности: (205)

130 Условие межфазного обмена массой Взяв данные в первой строке таблицы 2, преобразуем уравнение (205) к виду (206) Воспользовавшись определениями (169) и (171)(41), (39) и сформулируем условие межфазного обмена массой следующим образом: (207)

Условие межфазного обмена импульсом 131 Определим (208) Сформулируем, используя данные второй строки таблицы 2, уравнение (205) так (209)

Используя определения (*), (169), (171), (185)–(189), полученное соотношение запишем в виде 132 (210) Приняв во внимание соотношение (*) и определение (193), получим (211)

133 Сделаем определение (212) Применив определения (195) и (212), сформулируем условие межфазного обмена импульсом: (213)

134 Условие межфазного обмена энергией Определим, по аналогии с (208) (214)

135 Определим (это было в предыдущей лекции): (****)

136 Используя данные третьей строки таблицы 2 и сделанное определение, уравнение (205) запишем как (215) Применив определения (**), (****), (155), (156), (192) – (197), получим (216) или, учитывая определение (200), (217)

137 Сделаем определения (218) (219) Сформулируем теперь условие межфазного обмена энергией: (220)

ДЗЯКУЙ ЗА ЎВАГУ СПАСИБО ЗА ВНИМАНИЕ THANK FOR YOUR ATTENTION