Термодинамика Термодинамические процессы 1 Термодинамические процессы идеального

* Термодинамика Термодинамические процессы 1 Термодинамические процессы идеального газа. Изменение состояния рабочего тела может осуществляться различными способами, среди которых выделяют четыре основных (след. слайд). (слайды 1 -25) 2 Энтропия идеального газа 3 Тепловая Ts-диаграмма

* Термодинамика Термодинамические процессы Изохорный – процесс протекает при постоянном объеме газа: v=const; связь между изменяющимися параметрами состояния (р и Т) при этом выражается законом Шарля р/Т = const. Изобарный – при постоянном давлении газа: p=const; изменяющиеся параметры состояния (v и. T) связаны между собой законом Гей-Люссака v/T = const. Изотермический – при постоянной температуре газа: T=const; связь между изменяющимися параметрами p и удельным объемом v выражается законом Бойля. Мариотта pv = const.

* Термодинамика Термодинамические процессы Адиабатный – все три параметра состояния: р, v, T изменяются, но при отсутствии теплообмена с окружающей средой: q=0. Политропный – такое изменение состояния газа, при котором переменными являются все три параметра состояния, связь между давлением и удельным объемом выражается формулой: Частными случаями политропного являются первые четыре процесса.

* Термодинамика Исследование политропных процессов 6. Теплота по I закону термодинамики: q = Δu+l. и через теплоемкость: q = cΔT. Политропную теплоемкость можно найти из выражения показателя политропы, с учетом , что cp/cv=k: c =cv (n – k) /(n – 1). 7. Изменение энтропии 8. Энергетический коэффициент: φ=Δu/q = (n – 1)/(n – k).

* Термодинамика Значение политропных процессов Уравнение политропных процессов pvn = const справедливо для любого из частных термодинамических процессов: - изохорный n = ∞: p 1/nv=p 1/∞v=p 0 v= v = const; const - изобарный n = 0: pv 0 = p = const; const - изотермический - адиабатный n = 1: pv = const или T = const; const n = k: pvk = const

* Термодинамика pv - диаграмма политропных процессов – политропные процессы p VIII VII n = -∞ v=const q>0 VI 0 I Δu>0 n=0 Δu<0 p = const II n=1 q<0 III T = const V n=k IV pvk=const n = +∞ v=const сжатие расширение v Рис. – Возможные термодинамические процессы

* Термодинамика Особенности политропных процессов Значение показателя политропы определяет расположение и характер протекания политропного процесса на pv-диаграмме (рис. ) Изотерма (рис. ) T=const разделяет процессы на две группы: Δu > 0 и Δu < 0. Адиабата также делит их на две группы: q > 0 и q < 0. Таким образом, по знакам изменения внутренней энергии и теплоты процессы расширения газа делятся на I, II и III группы.

* Термодинамика Энтропия идеального газа Обозначим через дифференциал энтропии выражение ds = dq/T, Дж/(кг. К). dq/T (1) Тогда теплоту можно определить как dq=Tds, то есть площадь под процессом в Ts-диаграмме. Найдем зависимости T=f(s) для термодинамических процессов подстановкой в (1) I закона термодинамики: ; (2) . (3)

* Термодинамика Изменение энтропии в термодинамических процессах Проинтегрировав выражения (2) и (3), получим изменения энтропии в политропных процессах: ; (4) . (5) Из (4) при v=const и из (5) при p=const получим изменения энтропии в изохорном и изобарном процессах: ; (6) . (7)

* Термодинамика Изображение термодинамических роцессов в Tsдиаграмме То есть изохора и изобара в Ts-диаграмме представляют собой логарифмические кривые. Причем изохора проходит круче изобары, так как при ΔT=idem: Δsp>Δsv из-за cp>cv. Изотерма в Ts-диаграмме отображается горизонтальной Ts прямой. Изображение адиабаты вытекает из анализа выражения dq=0=Tds. Td

* Термодинамика Тепловая Ts-диаграмма Так как T ≠ 0, то ds = 0, следовательно s=const – это и есть уравнение адиабаты в Ts-диаграмме. На следующем Рис. (слайд) представлена Ts-диаграмма Ts термодинамических процессов. Площадь под процессом в Ts-диаграмме представляет собой теплоту, поэтому она называется тепловой диаграммой.

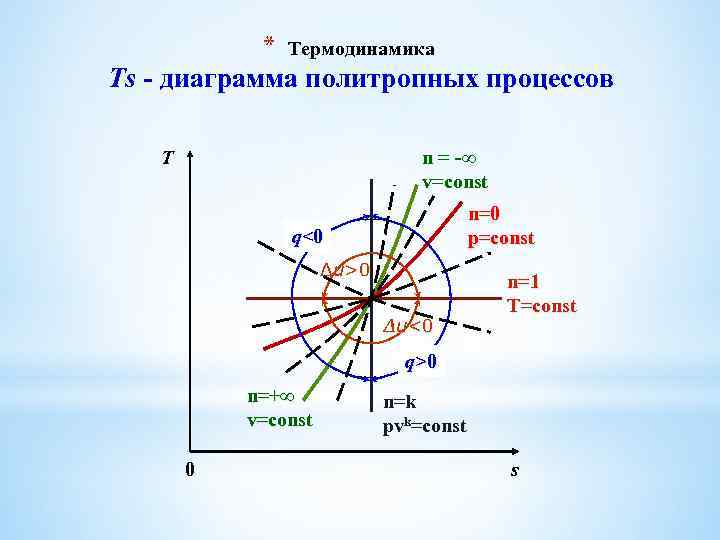* Термодинамика Ts - диаграмма политропных процессов T n = -∞ v=const n=0 p=const q<0 Δu>0 Δu<0 n=1 T=const q>0 n=+∞ v=const 0 n=k pvk=const s