ТЕРМОДИНАМИКА ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ НТ-10 Термодинамика поверхностных явлений

ТЕРМОДИНАМИКА ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ НТ-10

Термодинамика поверхностных явлений и дисперсных систем Поверхностные явления разделяют на : p физические, p химические, p электроповерхностные. p

Термодинамика поверхностных явлений и дисперсных систем В случае физических поверхностных явлений определяющую роль играет поверхностное натяжение – избыточная (по сравнению с внутренним объемом жидкости или твердого тела) свободная энергия поверхности, отнесенная к единице площади. p Эта избыточная энергия вызывает в дисперсных системах процессы, которые ведут к уменьшению поверхности. p

Термодинамика поверхностных явлений и дисперсных систем p p p Пример таких процессов – самопроизвольное слияние (коалесценция) капель в эмульсиях и аэрозолях и газовых пузырьков в пенах. Другой пример- в условиях неневесомости капли и газовые пузырьки приобретают сферическую форму, которая соответствует минимуму их поверхности. Это положение было подтверждено экспериментально в одном из первых космических полетов. Большую группу физических поверхностных явлений составляют капиллярные явления. Для них характерно сильное влияние кривизны жидкой или твердой поверхности.

Термодинамика поверхностных явлений и дисперсных систем Химические поверхностные явления сопровождаются значительными изменениями состава и структуры тонких поверхностных слоев жидкостей и твердых тел. p Наиболее важное– адсорбция (хемосорбция). p

Термодинамика поверхностных явлений и дисперсных систем Основными характеристиками электроповерхностных явлений служат: p электрический заряд и p электрический потенциал поверхности раздела дисперсной фазы и дисперсионной среды. p

Термодинамические закономерности формирования поверхностного слоя p p p Основным условием равновесия в гетерогенных системах является положительное значение энергии Гиббса образования межфазной поверхности. Молекулы вещества, локализованные в межфазных слоях, обладают избыточной энергией по сравнению с молекулами вещества, распределенными в объеме гомогенной фазы дисперсных систем (так как появляются на поверхности в результате разрыва межмолекулярных связей). Вследствие этого увеличение площади межфазной поверхности сопровождается увеличением поверхностной энергии (ΔG>0).

Термодинамические закономерности формирования поверхностного слоя Обратный процесс- уменьшение площади межфазной поверхности – сопровождается понижением значения поверхностной энергии (ΔG<0), т. е. протекает самопроизвольно. p Таким образом, поверхностный слой формируется в результате самопроизвольного уменьшения поверхностной энергии. p

Термодинамические закономерности формирования поверхностного слоя Самопроизвольное уменьшение поверхностной энергии может происходить за счет: p уменьшения площади межфазной поверхности в результате агрегации частиц дисперсной фазы (коагуляция твердых частиц или коалесценция капель жидкости); p снижения поверхностного натяжения в результате адгезии, адсорбции, образования двойных электрических слоев и других явлений. p

Термодинамические закономерности формирования поверхностного слоя p Возникновение поверхностных явлений является следствием стремления системы к самопроизвольному уменьшению поверхностного натяжения на границе раздела фаз.

Основные понятия и определения Термодинамическая система – тело или группа тел, находящихся во взаимодействии, мысленно или реально обособленные от окружающей среды. p Гомогенная система – система, внутри которой нет поверхностей, разделяющих отличающиеся по свойствам части системы (фазы). p Гетерогенная система – система, внутри которой присутствуют поверхности, разделяющие отличающиеся по свойствам части системы. p

Основные понятия и определения p p Фаза – совокупность гомогенных частей гетерогенной системы, одинаковых по физическим и химическим свойствам, отделённая от других частей системы видимыми поверхностями раздела. Изолированная система – система, которая не обменивается с окружающей средой ни веществом, ни энергией. Закрытая система – система, которая обменивается с окружающей средой энергией, но не обменивается веществом. Открытая система – система, которая обменивается с окружающей средой и веществом, и энергией.

Основные понятия и определения p p p Совокупность физических свойств системы в рассматриваемых условиях называют термодинамическим состоянием системы. Различают равновесное (стационарное) и неравновесное (нестационарное) состояния термодинамической системы. Макроскопические величины (т. е. величины, которые характеризуют тело в целом), характеризующие физические свойства тела в данный момент, называются термодинамическими параметрами состояния. Последние разделяются на интенсивные (не зависящие от массы тела) и на экстенсивные (пропорциональные массе тела).

Основные понятия и определения Переменные, значения которых зависят от общего количества вещества в системе, называются экстенсивными (Vсистемы, ее масса m, или число молей n в ней). p В противоположность им, переменные, не зависящие от количества и имеющие определенное значение в каждой точке системы называются интенсивными (Т, Р, мольная доля ХI i-того компонента). p

Основные понятия и определения p p В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению, например температуру, давление, концентрацию и т. д. Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть термодинамический процесс. Обратимый процесс – процесс, допускающий возможность возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Равновесный процесс – процесс, при котором система проходит через непрерывный ряд равновесных состояний.

Основные понятия и определения p p p Первое начало термодинамики утверждает, что при превращении одной формы энергии в другую полная энергия системы не изменяется, однако не указывает никаких ограничений относительно возможности этого процесса. Самопроизвольный процесс – процесс, который может протекать без затраты работы извне, причем в результате может быть получена работа в количестве, пропорциональном произошедшему изменению состояния системы. Самопроизвольный процесс может протекать или обратимо, или необратимо.

Основные понятия и определения p p Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса. Далее, второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера.

Основные понятия и определения p Совместное аналитическое выражение двух начал термодинамики для обратимых процессов: Для необратимых процессов можно записать неравенства: Т. о. , работа обратимого процесса всегда больше, чем того же процесса, проводимого необратимо.

Основные понятия и определения p p p Если рассматривать изолированную систему (δQ = 0), то для обратимого процесса d. S = 0, а для самопроизвольного необратимого процесса d. S > 0. В изолированных системах самопроизвольно могут протекать только процессы, сопровождающиеся увеличением энтропии. Энтропия изолированной системы не может самопроизвольно убывать. Оба этих вывода также являются формулировками второго начала термодинамики

Основные понятия и определения p Энтропия - есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана: p С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом: Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.

Основные понятия и определения p p При T = 0 любое вещество может находиться только в твердом состоянии. При нагревании вещества возможен его переход в жидкое и затем в газообразное состояние; для фазовых переходов, происходящих в изобарно-изотермических условиях, изменение энтропии равно приведенной теплоте фазового перехода: Таким образом, нагревание вещества без фазовых переходов сопровождается непрерывным ростом энтропии; при фазовом переходе происходит скачкообразное изменение энтропии. Графическая зависимость энтропии вещества от температуры приведена на рисунке 1.

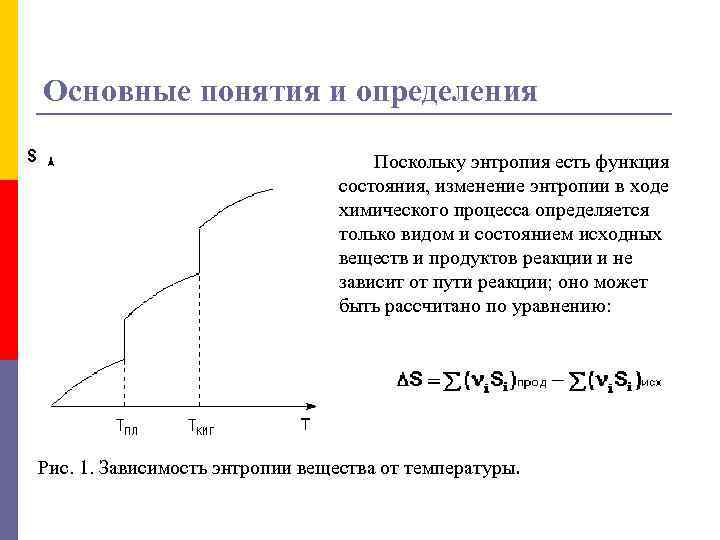Основные понятия и определения Поскольку энтропия есть функция состояния, изменение энтропии в ходе химического процесса определяется только видом и состоянием исходных веществ и продуктов реакции и не зависит от пути реакции; оно может быть рассчитано по уравнению: Рис. 1. Зависимость энтропии вещества от температуры.

Термодинамические функции состояния системы p p p Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса) и изохорно-изотермический потенциал (свободная энергия Гельмгольца).

Термодинамические функции состояния системы p p Поведение всякой термодинамической системы в общем случае определяется одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего противоположную тенденцию – стремление системы к максимальной неупорядоченности. Если для изолированных систем (ΔН = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной изменения энтропии системы ΔS, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности самопроизвольного процесса является изменение энтальпии ΔН,

Термодинамические функции состояния системы то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. p Направление и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии: p Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения. p

Термодинамические функции состояния системы p Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса, которую обозначим Amax (поскольку работа процесса, проводимого равновесно, максимальна) Преобразуем выражение последнее сгруппировав члены с одинаковыми индексами:

Термодинамические функции состояния системы p Введя обозначение: получаем: Данная функция - есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.

Термодинамические функции состояния системы p Закрытую систему, находящуюся в изобарноизотермических условиях, характеризует изобарноизотермический потенциал G: Поскольку –ΔF = Amax, можно записать:

Термодинамические функции состояния системы p p p Величину А'max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах. Условия самопроизвольного протекания процессов в закрытых системах: Изобарно-изотермические (P = const, T = const): ΔG < 0, d. G < 0 ΔF < 0, d. F < 0

Термодинамические функции состояния системы p p p Экзотермические реакции; ΔH < 0. а) Если ΔS > 0, то ΔG всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно. б) Если ΔS < 0, реакция будет идти самопроизвольно при ΔН > TΔS (низкие температуры). 2. Эндотермические реакции; ΔH > 0. а) Если ΔS > 0, процесс будет самопроизвольным при ΔН < TΔS (высокие температуры). б) Если ΔS < 0, то ΔG всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.

Термодинамические функции состояния системы p p p p Протекание самопроизвольного процесса в термодинамической системе сопровождается уменьшением свободной энергии системы (d. G < 0, d. F < 0). условием термодинамического равновесия в закрытой системе является минимальное значение соответствующего термодинамического потенциала: Изобарно-изотермические (P = const, T = const): ΔG = 0 d. G = 0, d 2 G > 0 Изохорно-изотермические (V = const, T = const): ΔF = 0 d. F = 0, d 2 F > 0 Состояние системы с минимальной свободной энергией есть состояние термодинамического равновесия: Термодинамическим равновесием называется такое термодинамическое состояние системы, которое при постоянстве внешних условий не изменяется во времени, причем эта неизменяемость не обусловлена каким-либо внешним процессом.

Природа поверхностной энергии Дисперсные частицы и дисперсионная среда относятся к различным фазам. p Система из разных фаз может существовать только в том случае, если межмолекулярные взаимодействия в различных фазах различны. p Единственной системой, в которой межмолекулярные взаимодействия отсутствуют, является идеальный газ. p Интенсивность молекулярных взаимодействий возрастает при переходе от реальных газов к твердым телам. p

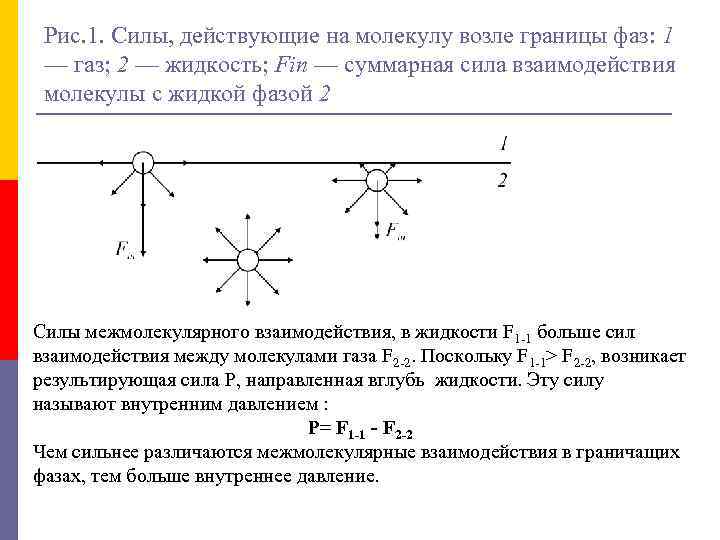Рис. 1. Силы, действующие на молекулу возле границы фаз: 1 — газ; 2 — жидкость; Fin — суммарная сила взаимодействия молекулы с жидкой фазой 2 Силы межмолекулярного взаимодействия, в жидкости F 1 -1 больше сил взаимодействия между молекулами газа F 2 -2. Поскольку F 1 -1> F 2 -2, возникает результирующая сила Р, направленная вглубь жидкости. Эту силу называют внутренним давлением : Р= F 1 -1 - F 2 -2 Чем сильнее различаются межмолекулярные взаимодействия в граничащих фазах, тем больше внутреннее давление.

Природа поверхностной энергии p p Наиболее важной характеристикой поверхности является поверхностное натяжение. Оно характеризует избыток поверхностной энергии, приходящийся на 1 м 2 межфазной поверхности. Поверхностное натяжение σ равно термодинамически обратимой, изотермической работе, которую надо совершить, чтобы увеличить площадь межфазной поверхности на единицу. где - термодинамически обратимая работа, затраченная на образование поверхности площадью так как работа совершается над системой, то она является отрицательной.

Природа поверхностной энергии p p Обычно работу совершают или при условии постоянства объема и температуры (V, Т = const), или при постоянных температуре и давлении (Р, Т = const). Рассмотрим оба варианта: 1) V, Т = const где F - свободная энергия Гельмгольца.

Природа поверхностной энергии p p p Поверхностное натяжение индивидуальных веществ на границе с газом понижается с повышением температуры: причем температурный коэффициент имеет практически постоянное отрицательное значение вплоть до температур, близких к критической. При критической температуре исчезает различие между граничащими фазами, и поверхностное натяжение становится равным нулю. Для большинства неполярных жидкостей температурная зависимость поверхностного натяжения линейная и в первом приближении может быть представлена соотношением:

САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ В ПОВЕРХНОСТНОМ СЛОЕ p p Самопроизвольно протекают только те процессы, которые приводят к уменьшению свободной энергии системы. Если процессы проводятся в условиях постоянства объема и температуры, они должны приводить к уменьшению свободной энергии Гельмгольца (d. F < 0). Процессы, протекающие при постоянных давлении и температуре, должны сопровождаться уменьшением свободной энергии Гиббса (d. G < 0). Если процессы в поверхностном слое не сопровождаются химическими реакциями, состав системы остается постоянным.

САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ В ПОВЕРХНОСТНОМ СЛОЕ p p Рассмотрим, какие процессы в поверхностном слое отвечают указанным условиям. Поверхностное натяжение - это свободная поверхностная энергия, приходящаяся на единицу площади межфазной поверхности. Значит, если процесс протекает при Соответственно для изобарно-изотермических процессов

САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ В ПОВЕРХНОСТНОМ СЛОЕ p Дифференцируя (2. 4) и (2. 5), получим: Условием самопроизвольного протекания как изохорноизотермических, так и изобарно-изотермических процессов является Для индивидуальных веществ поверхностное натяжение постоянно

САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ В ПОВЕРХНОСТНОМ СЛОЕ p В этих случаях самопроизвольно могут протекать процессы, сопровождающиеся уменьшением площади межфазной поверхности К поверхностным явлениям, связанным с уменьшением поверхности, можно отнести: • стремление капель жидкости или пузырьков газа принять сферическую форму (сферические частицы имеют самую маленькую удельную поверхность); • слипание твердых частиц дисперсной фазы (коагуляция); • слипание капель в эмульсиях или пузырьков газа в пенах (коалесценция); • рост кристаллов.

САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ В ПОВЕРХНОСТНОМ СЛОЕ p Если площадь межфазной поверхности остается постоянной условие (2. 8) может выполняться за счет уменьшения поверхностного натяжения которое может быть обусловлено процессом адсорбции.

Поверхностное натяжение p Поверхностное натяжение — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объем системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.

Поверхностное натяжение p p p Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости

Поверхностное натяжение (σ) — это работа, которую требуется затратить для образования единицы поверхности (размерность Дж/м 2). p Поверхностное натяжение (σ) — это сила, действующая тангенциально (по касательной) к поверхности, отнесенная к единице длины контура, ограничивающего поверхность раздела фаз, и препятствующая ее самопроизвольному увеличению (размерность Н/м). p

Поверхностное натяжение p Поверхностное натяжение (σ) — это мера избытка поверхностной энергии, приходящегося на единицу площади поверхности, который возникает за счет нескомпенсированности сил межмолекулярных взаимодействий у молекул поверхностного слоя.

Поверхностное натяжение p p p Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует. Сила поверхностного натяжения пропорциональна длине того участка контура, на который она действует. Коэффициент пропорциональности γ — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.

Поверхностное натяжение Зависимость от температуры p С увеличением температуры величина поверхностного натяжения уменьшается и становится нулем при увеличении температуры до критической. p

Способы определения p p Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами.

Поверхностное натяжение p p p В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения. Например, для раствора мыла после перемешивания поверхностное натяжение 58 Дж/м², а после отстаивания — 35 Дж/м². То есть поверхностное натяжение меняется. До установления равновесного оно будет динамическое.

Свойства дисперсных систем p p p Наиболее характерные свойства дисперсных (в особенности высокодисперсных, наноразмерных) систем определяются явлениями, происходящими на поверхности раздела фаз - поверхностными явлениями. Молекулы конденсированных фаз, находящиеся в поверхности раздела, обладают избыточной энергией по сравнению с молекулами в объеме из-за нескомпенсированности их межмолекулярных взаимодействий. Это порождает возникновение на поверхности раздела поверхностных сил и избытка энергии – поверхностной энергии.

Свойства дисперсных систем Особенность высокодисперсных и ультрадисперсных систем заключается в том, что их свойства зависят не только от химического состава образующего их вещества, но и от размера частиц дисперсной фазы. p Это означает, что поверхностная энергия определяет объемные свойства тел. p Зависимость свойств от размера частиц называют размерным или масштабным, эффектом. p

Свойства дисперсных систем Размерные эффекты, наблюдаемые в дисперсных системах, можно разделить на две большие группы. p 1. Эффекты, связанные с кривизной поверхности жидкой или газовой дисперсной частицы p 2. Эффекты, связанные с влиянием размера частиц на физические и химические свойства веществ. p

Особенность термодинамических свойств наносред p p p Из классической термодинамики следует, что изменение внутренней энергии системы d. U определяется количеством поступающей в нее теплоты δQ и совершенной ею работы δА: d. U = δQ – δА Переданное системе количество теплоты определяется через термодинамическую функцию как Td. S, где Т- температура, d. S – изменение энтропии. Совершенная системой работа для наносред в общем случае определяется суммой работ, во-первых, против сил внешнего давления pd. V, где р- давление, а d. V – изменение объема. И во-вторых, против сил поверхностного натяжения при создании новой поверхности площадью S, равной –σds, где σ – поверхностное натяжение, а знак минус указывает на увеличение энергии системы при увеличении площади поверхности.

Особенность термодинамических свойств наносред p p p Итоговое уравнение для расчета изменения внутренней энергии дисперсной системы будет выглядеть следующим образом: d. U = Td. S – pd. V + σds (1) Определим соотношения для свободных энергий Гельмгольца и Гиббса для наносред. В термодинамике функция Гельмгольца определяется как: F = U – TS, а ее дифференциал, соответственно, равен : d. F = d. U – Td. S – Sd. T. Подставляя d. U из выражения (1) получим: d. F = – pd. V + σds – Sd. T. Таким образом, при постоянной температуре дифференциал функции Гельмгольца определяется следующим соотношением: d. F = – pd. V + σds

Особенность термодинамических свойств наносред p p p p Функция Гиббса по первому закону термодинамики определяется как: G = H – TS, а энтальпия равна : Н = U + p. V. Следовательно, дифференциал функции Гиббса будет равен: d. G = d. U + pd. V + Vd. P – Td. S – Sd. T. С учетом выражения (1) : d. G = - Sd. T + Vd. P + σds (2) Следовательно, в условиях постоянства давления и температуры увеличение свободной энергии Гиббса в наносредах за счет роста площади свободной поверхности равно: d. G = σds (3)

Особенность термодинамических свойств наносред p p p Полученные соотношения показывают, что наносреды по сравнению с материалами в массивном состоянии прочих равных условиях обладают большей энергией на величину σds. Другими словами, при постоянных температуре и давлении энергия наносред может уменьшится за счет сокращения площади поверхности. Следовательно, дисперсные фазы, стремясь уменьшить свою энергию, должны самопроизвольно укрупняться. отличие свойств наноматериалов от массивных объектов в значительной степени вызвано увеличением роли поверхности при уменьшении их линейных размеров

Изменение фазовых равновесий в наноразмерных средах. p p p В наносредах происходит изменение фазовых состояний вещества. В частности, установлено смещение температур плавления и полиморфных превращений, стабилизация неравновесных состояний, а также образование фаз, которые в массивных образцах не наблюдаются. Если в массивном материале, в котором существовали фазы 1 и 2, при какой либо температуре Т, устойчивая фаза 1, т. е. Fv 1 < Fv 2 (где Fv – объемное слагаемое свободной энергии), то для образца в наносостоянии с учетом поверхностной энергии может выполняться условие: Fv 1 + Fs 1 > Fv 2 + Fs 2 , где Fs – поверхностное слагаемое свободной энергии. В этом случае устойчивой становится фаза 2.

Изменение фазовых равновесий в наноразмерных средах. p p p Уравнение Лапласа показывает, что давление внутри искривленной поверхности всегда больше наружного давления. Эта разность падает до нуля, если радиус кривизны становится бесконечно большим, т. е. в случае плоской поверхности. Наночастицы имеют очень большой радиус кривизны, поэтому разность давлений для них должна быть очень велика. Фазы, разделенные поверхностью с ненулевой кривизной, могут находится в равновесии только при различных давлениях внутри фаз: ∆р = 2σ (1/R 1 + 1/R 2)

Изменение температуры плавления в наноматериалах p p p Для наноразмерных материалов обнаружено, что они могут плавиться при более низкой температуре, чем табличная для данного вещества. Можно сформулировать даже более строгое утверждение: температура плавления наночастиц тем ниже, чем меньше их размер. Как показываю экспериментальные результаты, этот закон выполняется достаточно хорошо. Например, наночастицы золота радиусом 5 нм плавятся на 176 градусов ниже табличного значения, а радиусом 70 нм – только на 5 градусов ниже. Иными словами, две наночастицы одного и того же вещества, но разных радиусов, расплавятся при различных температурах.

Изменение температуры плавления в наноматериалах p p p На рисунке 2 показано, как изменяется температура плавления наночастиц из алюминия при уменьшении их размеров. Видно, что температура плавления частицы размером 4 нм на 140 о. С меньше, чем у образца алюминия обычных размеров. Зависимости, аналогичные той, которая показана на рис. 2, были получены для многих металлов. Так, при уменьшении диаметра наночастиц из олова до 8 нм их температура плавления падает на 100 С (от 230 С до 130 С). При этом самое большое падение температуры плавления (более чем на 500 С ) было обнаружено у наночастиц золота.

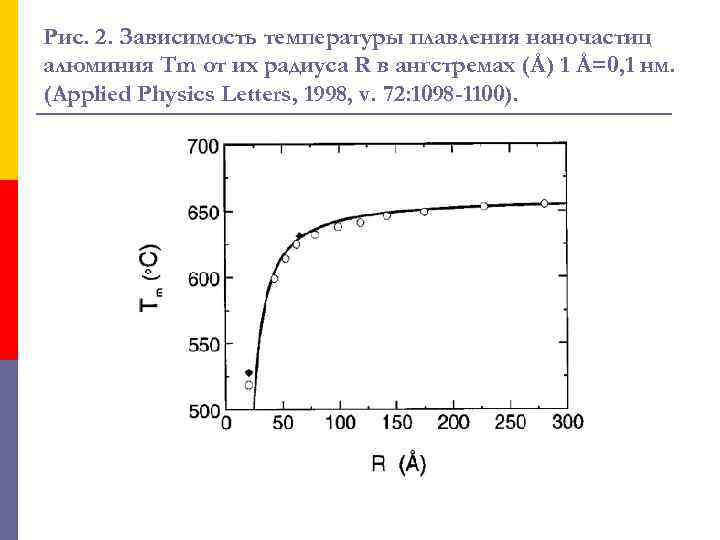Рис. 2. Зависимость температуры плавления наночастиц алюминия Tm от их радиуса R в ангстремах (Å) 1 Å=0, 1 нм. (Applied Physics Letters, 1998, v. 72: 1098 -1100).

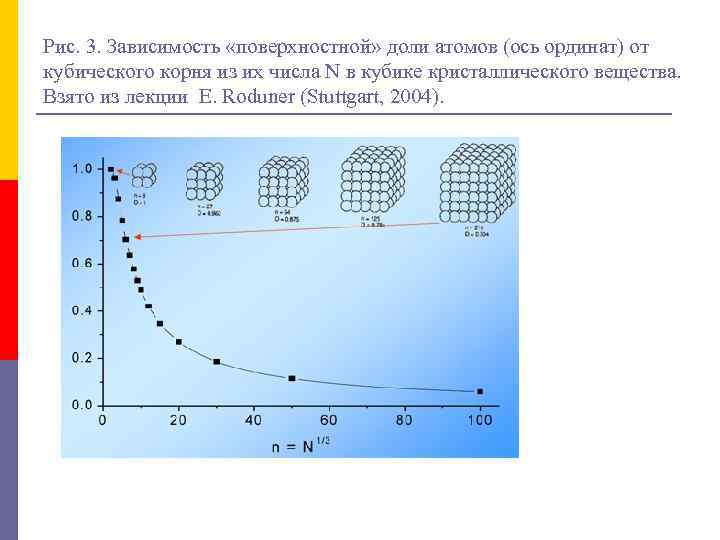Рис. 3. Зависимость «поверхностной» доли атомов (ось ординат) от кубического корня из их числа N в кубике кристаллического вещества. Взято из лекции E. Roduner (Stuttgart, 2004).

Количественные характеристики дисперсных систем

Количественные характеристики дисперсных систем

Количественные характеристики дисперсных систем

Размерные эффекты p p p p Размерный эффект – зависимость удельной характеристики (или интенсивного параметра) вещества от размера его частиц. В качестве такой характеристики могут быть: - термодинамические свойства; - параметры кристаллической решетки; - прочность, пластичность; - транспортные свойства (диффузия, электронная и ионная проводимость); - оптические и магнитные свойства; - реакционная способность (скорость и механизм химических реакций);

Размерные эффекты в гомогенных системах : p 1. «Обычные» размерные эффекты, связанные с вкладом поверхностной энергии или размерные эффекты I рода. Характерны для любых систем. p 2. Фазовые размерные эффекты (размерные эффекты II рода), которые невозможно объяснить вкладом поверхности; они определяются всем коллективом атомов в системе. Наблюдаются только в наночастицах и наносистемах. p

Размерные эффекты p p p Все размерные эффекты можно качественно разделить на 2 типа: - «слабые» размерные эффекты (I рода), обусловленные вкладом поверхности без существенного изменения свойств вещества; - «сильные « размерные эффекты (размерные эффекты II рода), в результате которых изменяются все фундаментальные характеристики вещества. Эти эффекты наблюдаются исключительно в наносистемах.

Размерные эффекты в гетерогенных системах представляют особый интерес, т. к. p - эти системы при определенных условиях термодинамически стабильны p - они обладают уникальными свойствами; p - эти свойства можно контролировать изменением состояния поверхности гетерогенного допанта. p

ОТЛИЧИЯ НАНОТЕРМОДИНАМИКИ ОТ КЛАССИЧЕСКОЙ ТЕРМОДИНАМИКИ p p p Первая монография по нанотермодинамике была опубликована в 1963 году Т. Хиллом. Нанотермодинамика вовсе не является пригодной исключительно для описания наносистем – все её утверждения, все формулы применимы к системам любого размера, включая макроскопические. Таким образом, нанотермодинамика является уточнением макроскопической (классической) термодинамики. Нанотермодинамика стремится точно учесть все эффекты, связанные с ограниченным числом молекул в исследуемой системе. Имеются следующие термодинамические особенности, характерные для наноструктур: - некоторые термодинамические соотношения могут не выполняться, т. к. появляется дополнительная степень свободы, обусловленная наличием тождественных и независимых малых частиц (систем);

ОТЛИЧИЯ НАНОТЕРМОДИНАМИКИ ОТ КЛАССИЧЕСКОЙ ТЕРМОДИНАМИКИ p p p - флуктуации термодинамических переменных становятся соизмеримы со средними значениями самих свойств; - проявляются значительные тепловые эффекты ∆Н; - точки фазового равновесия имеют тенденцию к сдвигу в область более низких температур; - изменяются температуры фазовых превращений; - некоторые термодинамические свойства (например, свободная энергия Гиббса G) могут терять монотонность.

ОТЛИЧИЯ НАНОТЕРМОДИНАМИКИ ОТ КЛАССИЧЕСКОЙ ТЕРМОДИНАМИКИ p p Из общих соображений следует, что наличие большого числа приповерхностных атомов должно оказывать значительное влияние на фононный спектр и связанные с ним термические свойства (теплоемкость, тепловое расширение, температуру плавления, решеточные составляющие теплопроводности и др. ). Отмечено, что в фононных спектрах наноструктур появляются дополнительные низко- и высокочастотные моды. Теплоемкость практически во всех случаях повышается (при T < 1°K немонотонно). Изменяются характеристическая температура (убывает) и фактор, отражающий атомные смещения (Дебая-Уоллера - возрастает). Уменьшается температура плавления.

Рекомендуемая литература